无伸缩缝桥梁荷载横向分布的影响参数分析

李秀芳，高轩能

（1.华侨大学 土木工程学院，福建 厦门361021；2.厦门理工学院 土木工程与建筑学院，福建 厦门361024）

无伸缩缝桥梁采用整体式桥台和整体浇筑的桥面系［1］，在荷载作用下，更多的因素参与了桥梁的整体受力.洪锦祥等［2］的研究表明，等效桩长是影响结构受力的因素之一.文献［3］的研究表明，在整体式桥梁中，温度、徐变和收缩产生的上部结构位移要由下部结构柔性桩吸收，桩的抗弯刚度是结构设计的要素；同时，下部结构对主梁约束作用会对主梁的应力产生影响［4］，宽跨比也影响着结构的受力.文献［3，5－6］的研究表明，较小的桥台高度对主梁的受力有利，而采用较大的桥台高度对桥台桩基础的受力有利，且主梁的伸缩量随桥台高度的增大而逐渐增大.彭大文等［7－8］以台后土体为研究对象，分析了常温下和季节性温度下台后被动土压力的大小及分布曲线，并提出了不同的填土方案.此外，文献［9］的研究表明，无伸缩缝桥梁取m＝mc时，其端跨边梁mc的放大系数应在5%～10%间.无伸缩缝桥梁由于结构的整体性，使得其荷载横向分布更为均匀，整体受力更为合理［10］.但是，目前梁桥的荷载横向分布及其影响因素的研究主要集中在传统简支类型桥梁上［11－13］.本文通过实桥验证模型的可行性，并研究等效桩长、桩的纵向抗弯刚度等参数对无伸缩缝桥梁mc的影响.

1 实桥数值模型的建立

以福建省上坂无伸缩缝大桥为例进行加载实验，分为单车偏载、两车偏载和两车对称3种工况，如图1所示.前期研究表明，无伸缩缝桥梁可以采用单个荷载P作用下的挠度影响线来研究其荷载横向分布规律［10］.选取端跨的跨中和四分之一跨截面为加载面和测试截面，监控不同工况下的结构变形.

建立ANSYS有限元空间模型，采用Solid 45单元模拟桥面系的主梁、横隔梁、铺装层、桥台和墩台结构；加载位置借助Shell 63单元实现；采用Shell 63单元模拟混凝土的防撞栏杆以实现其对桥面系刚度的贡献；采用Combin 39单元模拟台后土体与结构的相互作用，按NCHRP的p－y设计曲线［14］选取弹簧刚度；采用Combin 14单元模拟桩周土体与桩的相互作用，由“M”法计算并取其刚度.全桥模型由49 866个单元组成，共有216 625个节点，如图2所示.

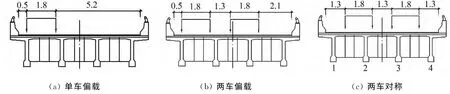
图1 荷载横向布置工况（单位：m）Fig.1 Transverse load case（unit：m）

数值模型计算结果与实验数据比对表明，挠度的模拟值与试验值吻合较好.图3为工况3（两车对称）跨中截面挠度δ比对.由于篇幅所限仅给出一幅图.从图3可知：δ理论／δ试验平均值为1.070，均方差为0.067.说明FEA模型很好地模拟了该桥荷载力学性能，即无伸缩缝桥梁的荷载横向分布较简支梁更加均匀，受力更合理.在此基础上对无伸缩缝桥梁的荷载横向分布系数影响参数进行分析.以钢筋混凝土刚接T型梁桥为例，基准跨径20m，基准模型主梁截面如图4所示.

图2 有限元模型图Fig.2 FEA model of test bridge

图3 挠度的试验与理论值比较 Fig.3 Comparison of deflection between calculation results and experimental results

图4 主梁横截面图（单位：mm） Fig.4 Cross－section of girder（unit：mm）

2 无伸缩缝桥梁mc的影响参数分析

2.1 等效桩长

采用一端固结的悬臂等效桩长（le）模拟无伸缩缝桥梁设计中涉及到的桩材料非线性［15－16］.选取不同le，比较边梁跨中挠度荷载横向分布影响线（influence line of transverse load distribution，ILTLD）的变化，并计算按两辆汽车最不利位置布载，得到不同le对ILTLD和mc的影响，如图5所示.图5中：η为单位荷载作用于跨中截面不同位置处传递到边梁跨中的荷载大小，下同.

图5 等效桩长对ILTLD和mc的影响Fig.5 Impact of equivalent pile length on ILTLD and mc

从图5可见：ILTLD的斜率随着等效桩长的增加而减小，即荷载横向分布逐渐均匀；随着等效桩长的增加，基于挠度影响线得到的mc逐渐减小，但当等效桩长超过10m后，这种影响的变化趋势就逐渐趋于收敛，le从2m变化到20m，mc差值达9%.

2.2 桩的纵向抗弯刚度

桩的转动惯量（IZ）对其纵向抗弯刚度的贡献最大.取le＝8m，桩截面为0.5m×0.7m的模型为基准，通过无量纲相对转动惯量来分析（下同）.＝I′Z／IZ，其中，IZ，I′Z分别为基准模型和改变后模型桩的纵向转动惯量.当不同时，主梁跨中的挠度ILTLD（η）变化如图6（a）所示；此时，不同的le取值对应的mc值变化，如图6（b）所示.

从图6可知：当le取值相同时，桩的纵向抗弯刚度越小，影响线越平缓，即荷载横向分布越均匀；等效桩长较短的桥梁mc受纵向抗弯刚度的影响比较明显，最大差值接近8%.但是，当le较短时，如果ˉI超过5，无伸缩缝桥梁的mc则超过具有相同上部结构传统简支梁桥梁的对应值.因此，在该类型桥梁中应尽量避免出现刚性桩.

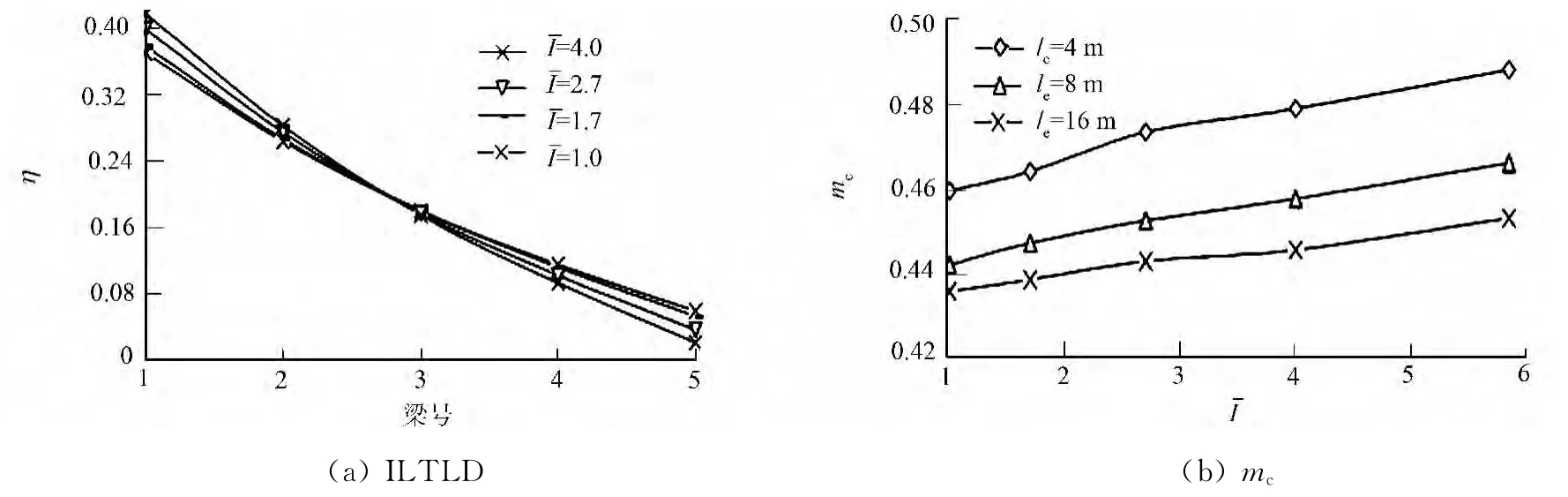
图6 桩的纵向刚度对ILTLD和mc的影响Fig.6 Vertical stiffness of pile′s influence on ILTLD and mc

2.3 桩的纵向相对刚度

桩的刚度取决于矩形桩的纵向刚度和等效桩长，故定义矩形桩的相对刚度（λ）为

式中：b为矩形桩长边；h为矩形桩短边；le为桩的等效长度.

不同h值下，λ与le和mc的关系，分别如图7，8所示.从图7可知：随着le的增大，λ均呈现下降趋势，且桩宽越大，下降越快.从图8可知：随着λ的增加，mc相应增大.le增大或纵向抗弯刚度变小都能引起λ变小，此时，桩的柔度越大，就越多地承担来自上部结构的荷载变形，mc就相应越小.

不同λ值下，桩宽对mc的影响如图9所示.由图9可知：mc对λ的变化较敏感，当λ值不变时，桩宽对mc几乎没有影响.因此，可忽略桩宽对mc的影响，但应关注λ值的影响.

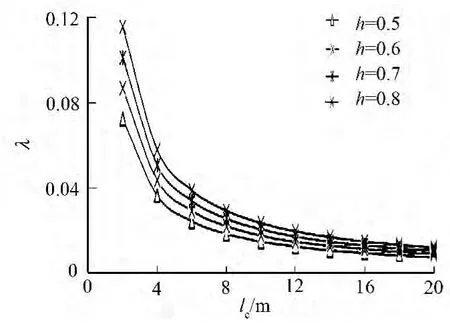
图7 λ与le的关系曲线Fig.7 Relationship curve betweenλand le

图8 mc与λ的关系曲线Fig.8 Relationship curve betweenλand mc

图9 桩宽对mc的影响Fig.9 Impact of pile′s width on mc

2.4 宽跨比

当桩取λ＝0.012时，挠度ILTLD（η）随宽跨比（B／L）的变化及按两辆汽车最不利布载得到mc值，如图10所示.从图10可见：ILTLD随着宽跨比的增大而逐渐变得平缓，荷载横向分布趋于均匀；mc随着宽跨比的加大而逐渐变小；宽跨比在0.4以内，荷载横向分布系数变化不大，mc差值不超过1.6%；宽跨比超过0.4后，mc随B／L的增加呈直线下降，B／L分别取0.4，0.8时，mc差值接近18%.

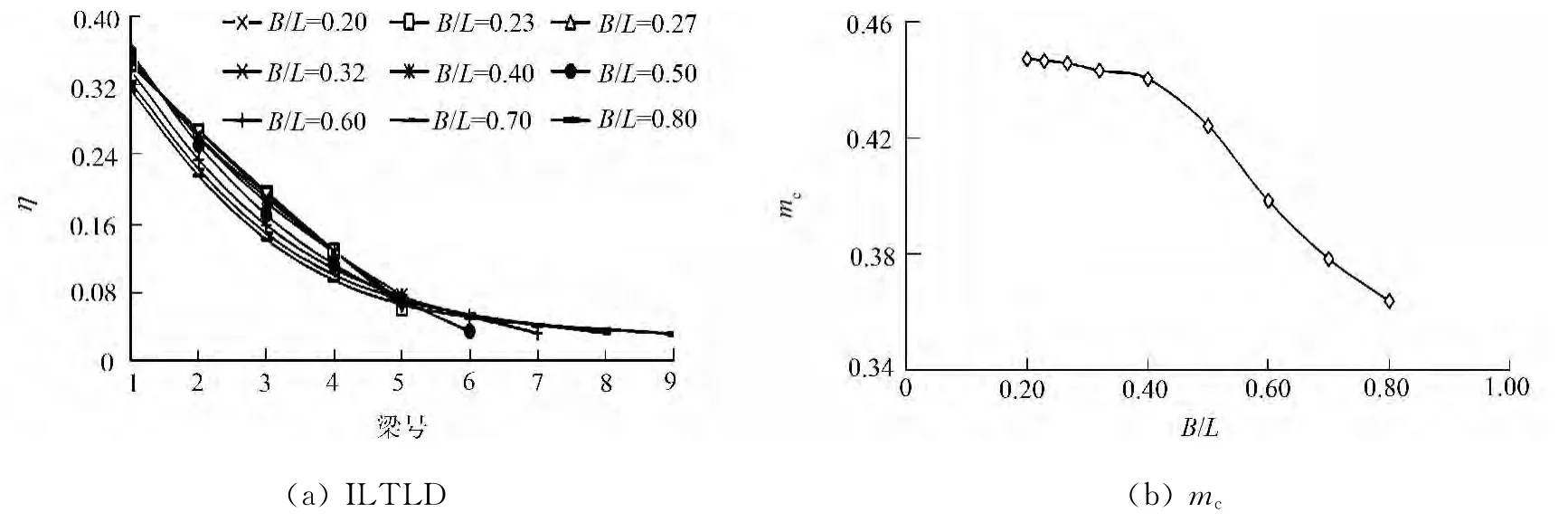
图10 宽跨比对ILTLD和mc的影响Fig.10 Impact of B／Lon ILTLD and mc

2.5 桥台高度

桥台高度（H）为从主梁顶到桩顶的距离.取H值为2，3，4和5m进行建模分析，当桩取λ＝0.012时，H对挠度ILTLD（η）和mc的影响，如图11所示.从图11可知：ILTLD的斜率随着桥台高度增大而增大；在相同λ下，mc随着桥台高度加大而变大；当桩的柔性越大即表现为λ值越小，差值的趋势越明显.因此建议在满足构造要求的前提下，尽可能减小整体式桥梁的桥台高度.

图11 桥台高度对ILTLD和mc的影响Fig.11 Impact of abutment height on ILTLD and mc

2.6 台后土压力作用

采用弹簧单元模拟桥台后土压力［2，17］，当桩取λ＝0.012时，不同土质对ILTLD（η）和mc的影响如图12所示.从图12可知：土质的密实程度越高，荷载横向分布影响线变得倾斜；mc随着土质密实程度变大而增大，当桩的柔性越大即λ值越小时，差别越明显，但差值均在1%以内，即mc受台后填土类型的影响很小.

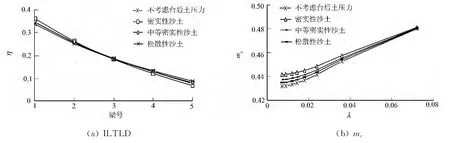
图12 不同台后土质对ILTLD和mc的影响Fig.12 Impact of different soil on ILTLD and mc

2.7 纵向抗弯刚度

桥台和桥面系的纵向抗弯刚度对mc的影响，如图13所示.从图13的桥台曲线可知：当桩取λ＝0.012时，不同相对转动惯量下，根据主梁跨中的挠度ILTLD按两辆汽车最不利布载得到mc的变化曲线.由此可见，不同桥面系相对刚度下，mc变化不大，差值在2%范围内，即可以忽略桥台纵向抗弯刚度对mc的影响.

从图13的桥面系曲线可知：mc随着桥面系纵向抗弯刚度的增大而相应变小，但是当ˉI超过1.5后就趋于收敛，两端极值相差在2%以内.况且，主梁高度的增加必定引起桥台高度的增大，台后土压力值的加大，乃至mc增大等一系列反应，这二者对mc的影响会相互抵消.因此，在无伸缩缝桥梁中，可以忽略桥面系的纵向抗弯刚度对mc的影响，这是无伸缩缝桥梁与传统简支桥梁区别之一［18］.

2.8 内横梁横向刚度

采用模型内横梁的相对横向转动惯量来分析其对mc的影响，如图14所示.从图14可知，内横梁根数的增加或横向刚度的增大，即变大，均会使得荷载横向分布影响线变得平缓，但此时却会加大边梁mc［10］.

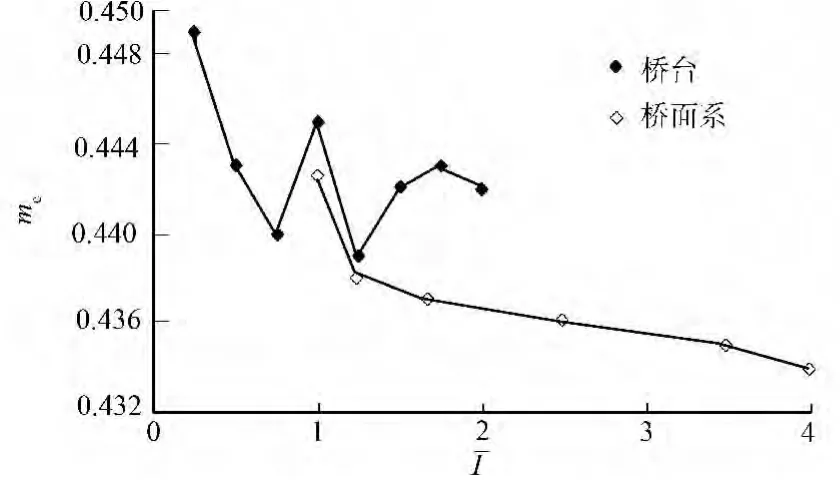
图13 纵向抗弯刚度对mc的影响Fig.13 Impact of longitudinal bending stiffness on mc

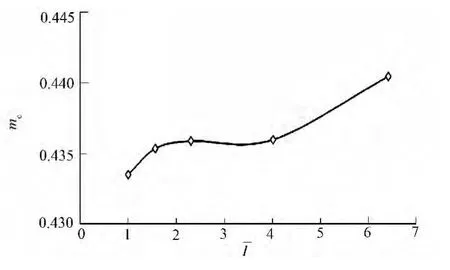
图14 内横梁横向相对抗弯刚度对mc的影响Fig.14 Impact of crossbeam relative lateral bending stiffness on mc

2.9 桥梁跨数

以单跨桥梁的边梁mc为基准，当跨数为1，2，3，4时，桥梁边跨mc分别为100%，97.4%，98.8%，98.4%，即单跨桥梁的mc比多跨桥梁的大，差值在3%范围内.由此可见，结构分析中可以偏于安全按单跨桥梁来考虑.

3 结论

通过实桥验证所建FEA模型能很好地模拟该桥在荷载作用下的力学性能，且数值模型的承载力是具有一定的安全储备.无伸缩缝桥梁的荷载横向分布较简支梁桥更加均匀，受力更合理；同时也验证了在全桥范围内近似取m＝mc的可行性.

通过参数分析，可知等效桩长、桩的纵向抗弯刚度、桩的纵向相对刚度、宽跨比对无伸缩缝桥梁的荷载横向分布影响较显著.等效桩长越长，桩的纵向抗弯刚度越小，桥梁边梁的mc越小.这两个参数的影响集中体现在相对刚度λ中，当桩的柔度越大即λ值越小时，mc值就越小；荷载横向分布影响线（ILTLD）随着宽跨比的增大逐渐平缓，mc逐渐变小.但是，宽跨比不大时，mc差值仅在1.6%范围内；宽跨比大于0.4，随着桥宽加大，mc呈直线下降，其最大差值可达17.34%.

［1］彭大文，林志平，洪锦祥.无伸缩缝桥梁的研究与实践［J］.公路，2006（8）：53－62.

［2］洪锦祥.整体式桥台桥梁的简化计算模型与受力性能研究［D］.福州：福州大学，2005：38－41.

［3］彭大文，陈朝慰，洪锦祥.整体式桥台桥梁的桥台结点受力性能研究［J］.中国公路学报，2005，18（1）：46－50.

［4］洪锦祥，彭大文.桩基础的整体式桥台桥梁受力性能研究［J］.中国公路学报，2002，15（4）：43－48.

［5］洪锦祥，彭大文.桥台刚度对整体式桥台桥梁受力性能的影响研究［J］.公路交通科技，2006，23（1）：77－81.

［6］PHARES B M，FARIS A S，GREIMANN L，et al.Integral bridge abutment－to－approach slab connection［J］.Journal of Bridge Engineering，2013，18（2）：179－181.

［7］彭大文，陈晓冬，袁燕.整体式桥台桥梁台后土压力的季节性变化研究［J］.岩土工程学报，2003，25（2）：135－139.

［8］洪锦祥，彭大文，汪新惠.整体式桥台桥梁的台后被动土压力研究［J］.福州大学学报：自然科学版，2003，31（6）：721－725.

［9］彭大文，陈朝慰，林志平，等.无伸缩缝桥梁荷载横向分布系数研究［J］.公路交通科技，2007，24（9）：51－56.

［10］李秀芳，吴锐福.整体式无伸缩缝桥梁荷载横向分布系数的模型试验与有限元分析［J］.公路交通科技，2013，30（12）：86－92.

［11］赵文杰.简支T型桥荷载横向分布系数计算方法的比较研究［J］.华东公路，2013（1）：20－23.

［12］王仕实，孙卓，蔡卡宏，等.基于梁格法在用简支梁桥荷载横向分布应用研究［J］.广州大学学报：自然科学版，2012，12（5）：56－60.

［13］项贻强，邢骋，邵林海，等.横向加固空心板梁桥荷载横向分布计算方法与试验研究［J］.中国公路学报，2013，26（2）：63－68.

［14］BARKER R M，DUNCAN J M，ROJIANI K B，et al.Manuals for the design of bridge foundations：Shallow foundations，driven piles，retaining walls and abutments，drilled shafts，estimating tolerable movements，load factor design specifications，and commentary［M］.Washington D C：Transportation Research Board，1991：4－7.

［15］ROBINSON B，SUAREZ V，ROBALINO P，et al.A point of fixity model for pile and shaft bents［M］.Denver：American Society of Civil Engineers，2007：20－25.

［16］CHEN Y.Assessment on pile effective lengths and their effects on design（Ⅰ）：Assessment［J］.Computers and Structures，1997，62（2）：265－286.

［17］WENDNER R，STRAUSS A，BERGMEISTER K.Jointless bridges：Performance assessment of soil－structure interaction［M］.Boca Raton：CRC Press，2011：1069－1076.

［18］姚玲森.桥梁工程［M］.北京：人民交通出版社，1995：12－18.