一类四阶奇异非线性积分边值问题正解的存在性
王全义,邹黄辉
(华侨大学 数学科学学院,福建 泉州362021)
1 预备知识
两端简单支撑的弯曲弹性梁的平行状态可用四阶两点边值问题

来描述[1],关于这类边值问题的正解存在性已受到广泛的研究[2-5],微分方程的积分边值问题在热传导、等离子物理、化学工程、流体力学等方面具有广泛的应用背景.因此,微分方程的积分边值问题受到许多学者的广泛关注[6-10].本文将研究四阶奇异非线性积分边值问题
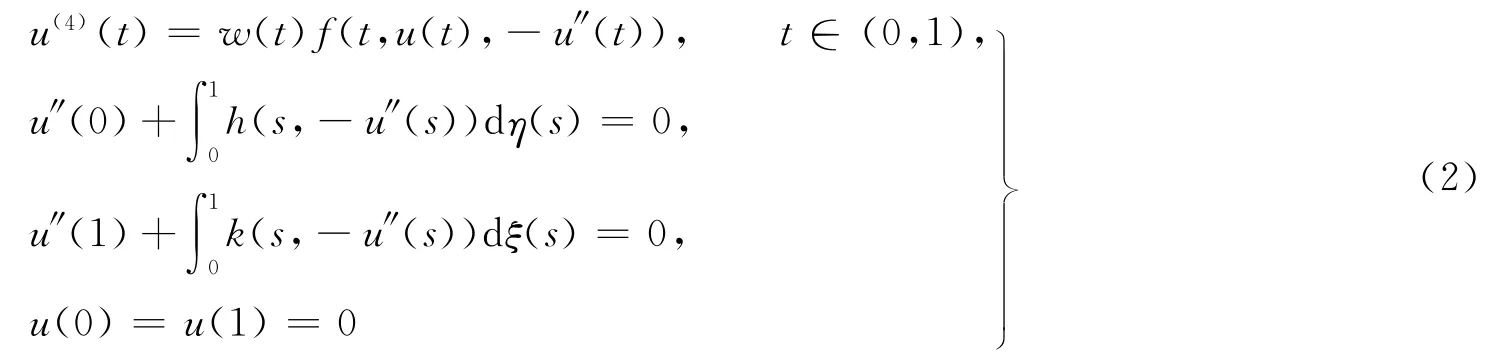
的正解的存在性.式(2)中:f∈C([0,1]×[0,+∞)×[0,+∞),(-∞,+∞));h,k∈C([0,1]×[0,+∞),[0,+∞));w∈C((0,1),[0,+∞));ξ(s)和η(s)在[0,1]上是非减的;在边值条件(2)中的积分是Riemann-Stieljes积分.
显然,非线性项f(t,u,p)是可变号的,且w(t)在t=0,1可能是奇异的.此外,当ξ(s)≡0,η(s)≡0,w(t)≡1时,边值问题(2)退化为问题(1).对于具非线性积分边界条件的四阶非线性微分方程的边值问题(2)的正解存在性问题很少有人研究过.
假设下面的条件成立:

H′1)设f∈C([0,1]×[0,+∞)×(0,+∞],(-∞,+∞)),且当[0,1]时,f(t,u,p)≥0.
2 一些引理
设X是Banach空间,K⊂X非空,且满足
1)对任意u,v≥0,任意x,y∈K,有ux+vy∈K;
2)若x∈K,-x∈K,则x=0,那么称K为X中的一个锥.
记空间E=C2[0,1],在E中定义范数,则E在范数‖x‖下成为一个Banach空间.在E中定义一个锥K,记Kr={x∈K∶‖x‖≤r},∂Kr={x∈K∶‖x‖=r},={x∈K∶r≤‖x‖≤R},其中:0<r<R.
引理1[11]设X是Banach空间,P是X中的一个锥,Ω1和Ω2是X中的开集,0∈Ω1,⊂Ω2,T∶P∩/Ω1→P是全连续算子,如果下列条件之一满足,即
1)若x∈P∩∂Ω1,则‖Tx‖≤‖x‖;若x∈P∩∂Ω2,则‖Tx‖≥‖x‖;
2)若x∈P∩∂Ω1,则‖Tx‖≥‖x‖;若x∈P∩∂Ω2,则‖Tx‖≤‖x‖.那么算子T在P∩(ˉΩ2/Ω1)中有不动点.
引理2函数G(t,s)定义为
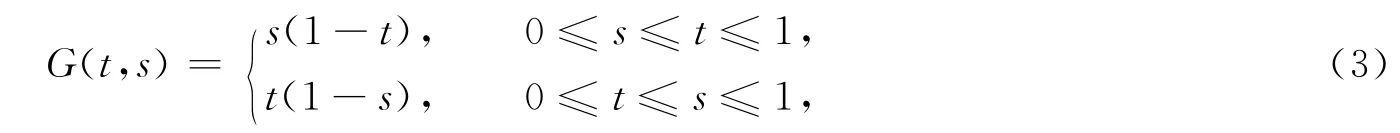
那么,当t,s∈[0,1]时,有

引理3假设条件H1),H2)成立,若如下的边值问题

有一个正解x(t),x(t)≥min{t,1-t}‖x‖,t∈[0,1],G(t,s)由式(3)定义,那么积分边值问题(2)至少有一个正解u(t),且
引理4假设条件H1),H2)成立,如果的积分方程

有一个正解x=x(t),G(t,s)由式(3)定义,那么x=x(t)是边值问题(5)的一个正解.
为了应用引理1,锥定义为
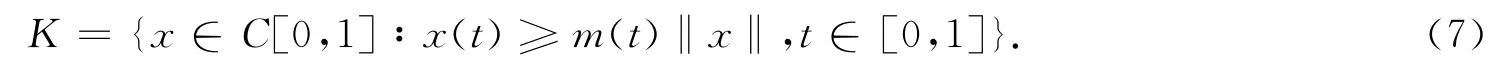
m(t)由式(4)给出.算子T∶K→C[0,1]定义为
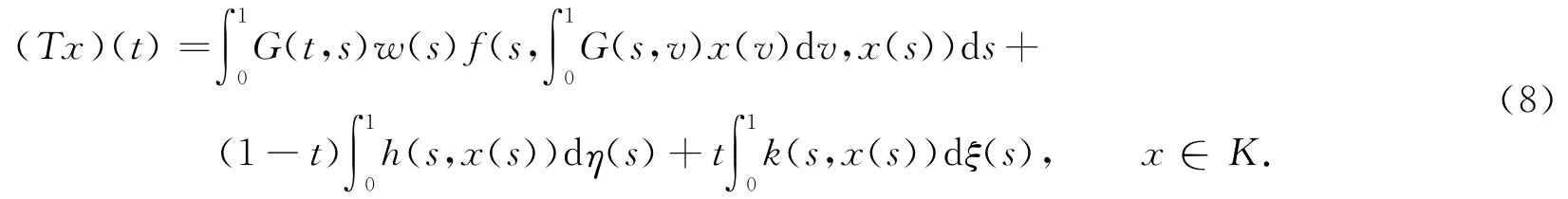
引理5假设条件H1),H2)成立,那么T(K)⊂K,而且T∶K→K是全连续的.
3 正解的存在性
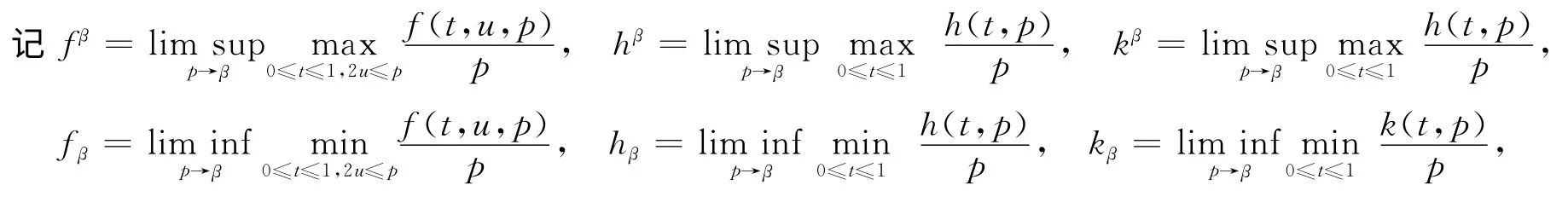
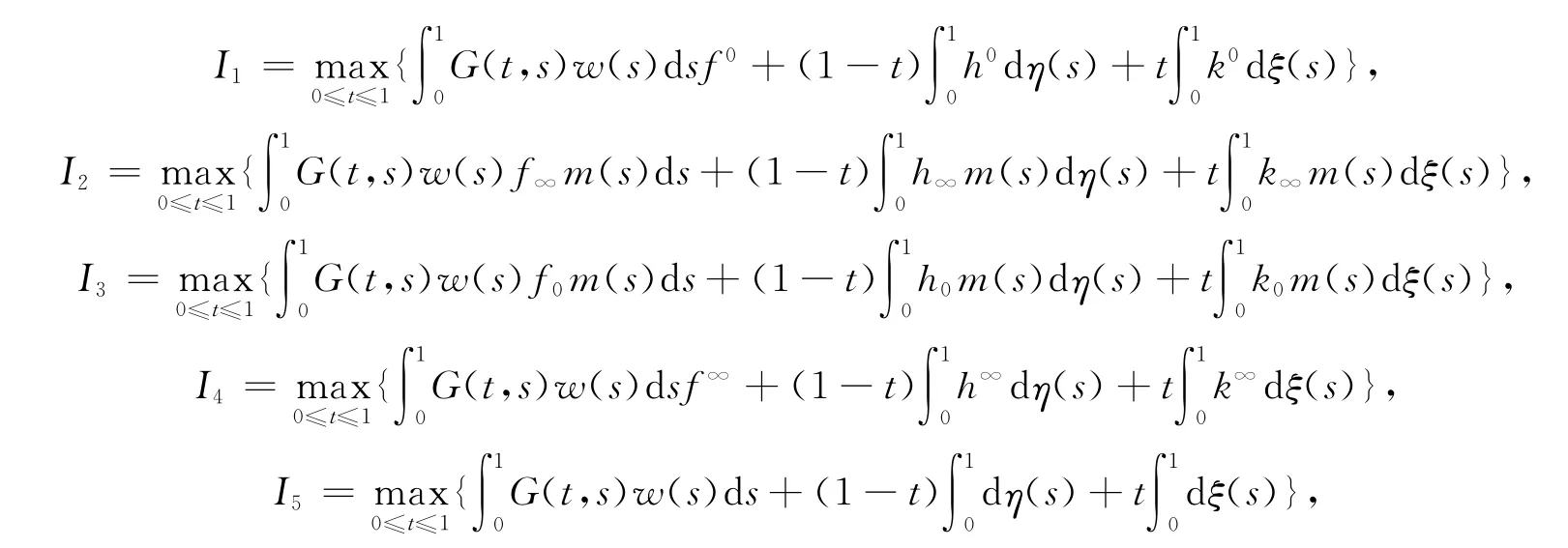
G(t,s)和m(t)分别由式(3),式(4)给出.
如果条件H2)成立,显然I5是有界的,且0<I5≤M+M0,其中
定理1假设条件H1),H2)成立,如果f∞≥0,I1<1<I2,则边值问题(2)至少有一个正解.
证明 考虑式(8)定义的算子T∶K→C[0,1],由引理5可知T∶K→K是全连续的.又因为I1<1,0<I5≤M+M0,因此存在ε1>0,使得I1+ε1I5<1.对此ε1>0,存在r1>0,使得当t∈[0,1],0<p≤r1,2u≤p时,就有

那么由式(6)~式(9),当t∈[0,1],t∈∂Kr1时,可得
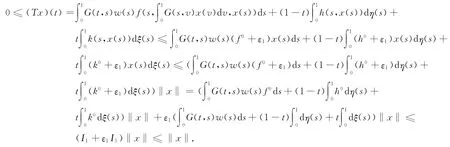
故有

因为I2>1,m(0)=m(1)=0,故存在ε2>0,0<δ<1/2,使得

对ε2>0,存在r22>0,使得当t∈[0,1],0≤2u≤p,p≥r22时,有
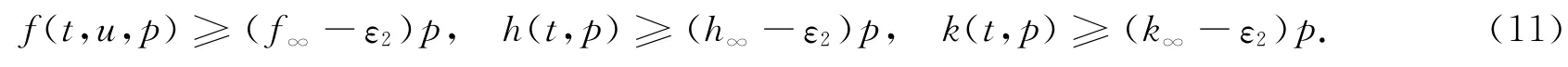
取r2=max{r1+1,δ-1r22},所以当t∈[δ,1-δ],x∈∂Kr2时,有

于是当x∈∂Kr2,t∈[0,1]时,由式(7),(11),(12)可得


故有

由引理4,式(10),(13)知算子T∶K∩(/Kr1)→K满足引理1中的所有条件.因此由引理1知有一个不动点x0∈ˉKr1,r2,r1≤‖x0‖≤r2,且x0(t)≥min{t,1-t}‖x0‖,t∈[0,1].由式(8),引理3,4知边值问题(2)至少有一个正解u0,且,u0(t)≥min{t,1-t}‖u0‖,t∈[0,1].定理1证毕.
在定理1的证明中,假设1<I2<+∞.但是对于I2=+∞,容易证明定理1也是成立的.
定理2假设条件H1),H2)成立,如果f∞,f0≥0,I4<1<I3,则边值问题(2)至少有一个正解.
在定理2中假设1<I3<+∞,但是当I3=+∞时,容易证明定理2的证明也是成立的.
假设以下条件成立:

由引理2得,条件H2),H′2)是等价的.
定理3设条件H1),H′2)成立,而且假设存在4个常数ρ1,ρ2,δ,λ,且ρ1>0,ρ2>0,ρ1≠ρ2,0<δ<1/2,0≤λ<1使得条件H3)为
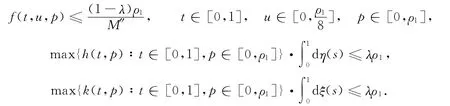
条件H4)为

那么积分边值问题(2)至少有一个正解u,使得在ρ2和ρ2之间.
因为当h(t,p)≡0,k(t,p)≡0,ξ(s)≡0,η(s)≡0,w(t)≡1,边值问题(2)退化为边值问题(1).这时在定理3中,,并且如果取λ=0,δ=1/4,那么立即可得
推论1假设H′1)成立,又存在两个正数ρ1,ρ2且ρ1≠ρ2使得

那么边值问题(1)至少有一个正解u,使得在ρ2和ρ2之间.
显然,推论1中的f(t,u,-p)是可以变号的,并且也不要求maxf0,minf0,maxf∞,minf∞∉{0,+∞},而且推论1中的条件H′3),H′4)也大大弱于文献[5]的定理中的条件H5),H6),因此推论1大大优于文献[5]的定理3.1.从而定理3推广和改进了文献[5]的定理3.1.
定理4假设条件H1),H2)成立,如果f∞,f0≥0,I2>1,I3>1,且存在b>0,使得,其中
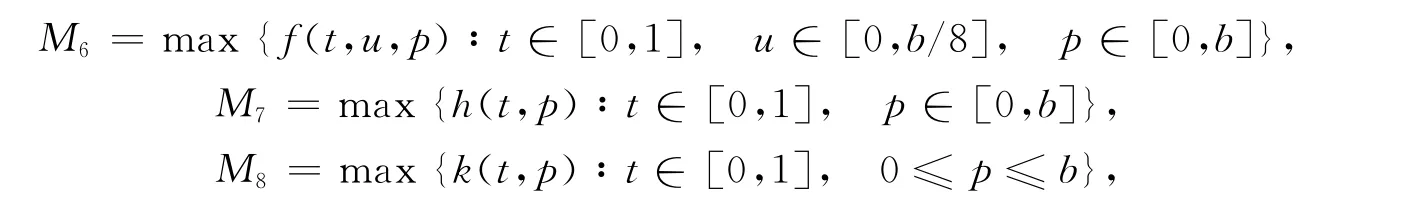
那么边值问题(2)至少有两个正解.
在定理4中,假设1<I2,I3<+∞,但是当I2=+∞或I3=+∞时,定理4仍然成立.
[1]GPTA C P.Existence and uniqueness theorem for a bending of an elastic beam equation[J].Appl Anal,1988,26(2):289-304.
[2]MA Ru-yun,XU Ling.Existence of positive solutions of a nonlinear fourth-order boundary value problem[J].Applied Mathematics Letters,2010,23(5):537-543.
[3]MA Ru-yun,XU Jia.Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem[J].Nonlinear Analysis,2010,72(1):113-122.
[4]CUI Yu-jun,ZOU Yu-mei.Existence and Uniqueness theorems for fourth-order singular boundary value problems[J].Computers and Mathematics with Applications,2009,58(7):1449-1456.
[5]LIU Bing.Positive solutions of fourth order two-point boundary value problems[J].Appl Math Comput.2004,148(2):407-420.
[6]张兴秋.奇异四阶积分边值问题正解存在唯一性[J].应用数学学报,2010,33(1):38-50.
[7]MA Hui-li.Symmetric positive solutions for nonlocal boundary value problems of fourth order[J].Nonlinear Analysis,2008,68(3):645-651.
[8]ZHANG Xue-mei,GE Wei-gao.Positive solutions for a class of boundary-value problems with integral boundary conditions[J].Computers and Mathematics with Applications,2009,58(2):203-215.
[9]KONG Ling-ju.Second order singular boundary value problems with integral boundary conditions[J].Nonlinear Analysis,2010,72(5):2628-2638.
[10]邹黄辉,王全义.一类四阶微分方程积分边值问题正解的存在性[J].华侨大学学报:自然科学版,2011,32(6):699-704.
[11]郭大均.非线性范函分析[M].济南:山东科学技术出版社,2002:314-315.

