快速流化床内气固两相流动态压力的实验研究
徐 俊,顾松园,钟思青,俞志楠,赵 玲
(1.中国石油化工股份有限公司上海石油化工研究院,上海,201208;2.华东理工大学化学工程联合国家重点实验室,上海,200237)
气固循环流态化是一种高效的气固接触技术。作为一种可持续操作、生产能力大、反应器内温度均匀等优点的装置系统,循环流化床被广泛应用于多个工业领域,如催化裂化工艺(FCC)、甲醇制烯烃(MTO)工艺的快速流化床反应器等。
快速床床层内气固两相的流动特性主要通过时均压力参数的测量进行研究,但时均参数只能反映气固两相流的宏观特性,对于局部、瞬时的流动参数不能给出精确的描述。气固流化床的压力波动信号中包含着床内气固两相流动的大量信息,综合反映了流化床的整体流化特性,是颗粒特性、流化床几何特性和气泡特性的综合反映[1]。研究流化床压力脉动产生的原因对认识流化床内的流动结构具有重要意义。对于流化床压力脉动产生的原因,有不同的研究结论[2,3]。Bi[4]总结了前人的研究成果,认为压力波动的原因是多方面的,包括气泡导致的波动、床体的振动和源于其他位置(如床表面、分布板和布气室)的压力波动的传播。Fan 等[5]采用统计方法对流化床中的压力脉动信号进行了分析,研究了流化床中包括分布板上射流区压力脉动的概率和统计特性,探讨了引起压力脉动的原因,认为流化床内的压力脉动不是直接由床高波动引起的,而是由气泡的形成、聚并以及气泡的运动所引起。Kang等[6]提出气泡的运动改变了气体在床内运动的形式和条件,也改变了乳化相的孔隙率,最后导致了压力波动。Bi 等[7,8]系统评述了鼓泡流化床的压力脉动问题,压力脉动产生的因素是复杂的,颗粒的物性、流化床的结构、气泡的聚并和破碎,分布器和风源等均可以对其产生影响。
文献研究结果表明,对于低气速下的气固流化床(如鼓泡床、湍动床),压力脉动的根源是由于气泡的存在,但是就局部点的压力脉动而言,它不仅和该点处的气泡运动有关,而且受到周围其它点处压力脉动的影响,是颗粒特性、床的几何特性、气泡运动特性等一系列因素的综合反映。本工作将实验考察快速流化床内的轴向动态压力,通过对动态信号的分析去认识流化床内气固两相流的瞬态参数特性以及气固两相之间的相互作用机制。
1 实验装置及方法
1.1 实验装置与方法
实验采用的是煤化工中常用的快速流化床装置与流程,如图1所示。来自压缩机的空气经过缓冲罐由流量计进入快速流化床中,推动来自经过返料阀控制的催化剂颗粒上行,在流化床顶部缩径进入上行管,气固在上行管经过快分后,催化剂颗粒顺流向下流化床沉降器后,再由返料管下行,返回快速流化床中,完成颗粒循环,气体经过沉降、旋风分离器分离后经过滤器排空。快速流化床直径(D)为200 mm,高5.5 m。实验所选用的固体物料为工业上常用的A 类催化剂颗粒,颗粒密度为1 300 kg/m3,堆积密度为700 kg/m3,颗粒平均粒径为65 μm。
表观气速由安装在进气管道上的V 锥流量计实时测得的气体流量除以流通截面积得到,实验的流化床表观气速(ug)控制为2 m/s。床层轴向压力分布的测量通过SYK-8 动态智能多点压力测试仪进行。压力脉动的测量高度(H)0.725、1.225、1.475、1.975、2.475、2.975 和3.475 m。
采用称重法对颗粒循环速率进行测量。实验采用的颗粒循环量(Gs)分别为1.50,7.53,12.32,19.87 kg/(m2·s)。

图1 快速流化床装置Fig.1 Schematic diagram of fast fluidized bed
1.2 分析方法
(1)统计方法
标准偏差分析是流化床压力脉动特性分析的常用方法[9,10]。本研究采用标准偏差来表征压力脉动的强度。将任意时刻的瞬态压力Pi分解为平均值与波动值P′之和。
任意一个测量点的压力标准偏差Sd为:

N为采样数据个数。Sd可以用于表征压力脉动的强度。
(2)功率谱分析
功率谱密度图像表征压力信号的能量在频域上的分布,以Fourier 级数和Fourier 积分为基础,用来描述信号在频率域上的各种分布[11]。谱分析的对象是离散信号,对于离散信号的频域分析采用的是离散Fourier 变换(DFT),它是对信号做频域分析的理论依据。但直接使用DFT 定义计算信号频谱时计算量较大,因此要转为采用快速Fourier 变换(FFT),FFT 是以较少计算量实现DFT 的快速算法,它使理论变成了实践,是数字信号分析与处理的强有力工具。
(3)多尺度小波分析
由于Daubechies 小波具有紧支集性、正交性,被广泛应用在流化床内动态信号的分析中[12,13]。对于正交小波,可用小波分解系数来表征信号的能量,对小波分解后的信号进行计算,通过各个尺度(即不同频段)的能量占原始信号总能量的分率,可分析动态压力在流化床中的特性。本研究采用Daubechies 小波函数(db5)将流化床内动态压力信号分解为13 个尺度,并计算各尺度能量分率在流化床内的分布。小波分解成的各尺度信息代表了不同频段上的信息。在小尺度上,细节对应着信号中的高频信息,而大尺度对应着信号的低频信息。本试验采样频率为400 Hz,在1 尺度上细节信息对应的频率大致为200~400 Hz,依次类推,13 尺度上对应的为0.05~0.1 Hz 的频段。
2 结果与讨论
2.1 压力时间序列
实验中由于流化床压力信号不可避免地受到各种干扰,因此在进行信号分析之前需要对信号进行滤波。Pence 等[14]在混沌研究中滤掉40 Hz 以上的信号,认为40 Hz 以上的信号为噪声;Bai 等[15]认为20 Hz 以上信号是噪声信号。因此如何判断噪声信号,需要针对具体的流态给出合理的判断。由于快速流化床处在较高气速下操作,床层不再以气泡为主要特征,压力脉动信号的能量集中在低频部分,综合考虑流化床信号的特性,本研究采用小波分析对信号进行去噪处理。
图2是流化床表观气速为2 m/s,不同颗粒循环量时各床层高度测压点的瞬时压力曲线。实验结果所示压力曲线具有明显的周期性脉动,在较低颗粒循环量[图2(a)]时,压力脉动的幅值较小,底部与顶部的压力脉动变化不大,压力脉动的频率较高,曲线呈锯齿型,主要是由于气体与颗粒的湍动、颗粒碰撞、颗粒团聚物的形成与破裂等高频部分的信号。颗粒循环量增大[图2(b、c、d)]以后,曲线出现了较为低频高幅的变化,此时曲线由两种不同成分的脉动叠加构成。一种脉动频率较低(周期约为0.3~1 s),幅值较大;另一种脉动频率较高,但幅值相对很小,曲线也呈锯齿型。顶部区域的压力脉动幅值比底部入口区域明显减小,但频率变化不大。

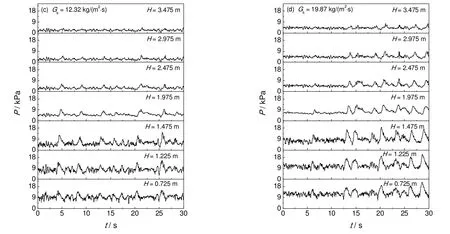
图2 流化床内的压力脉动曲线Fig.2 Pressure fluctuations in the fluidized bed
2.2 动态压力的标准偏差分析
流化床内压力脉动强度随颗粒循环速率的变化曲线如图3所示。在低循环速率[Gs=1.50 kg/(m2·s)]时,标准偏差值由上至下变化不大,普遍偏低,约为0.2 kPa,表明在这种流态下的脉动幅值很小,且沿床层高度的变化不大;随颗粒循环速率Gs的增加,增大至7.53 kg/(m2·s)时,由于床层底部逐渐建立密相料位,且随着循环速率的逐渐增大,密相料位高度也逐渐升高,而床层沿程的局部压力脉动的标准偏差值也随着Gs的增大逐渐明显增大。值得注意的是,在循环速率较高时,底部的压力脉动标准偏差与顶部之间存在着明显的转折,这与流化床内部流场轴向不同流态及稀密相分界面有关。
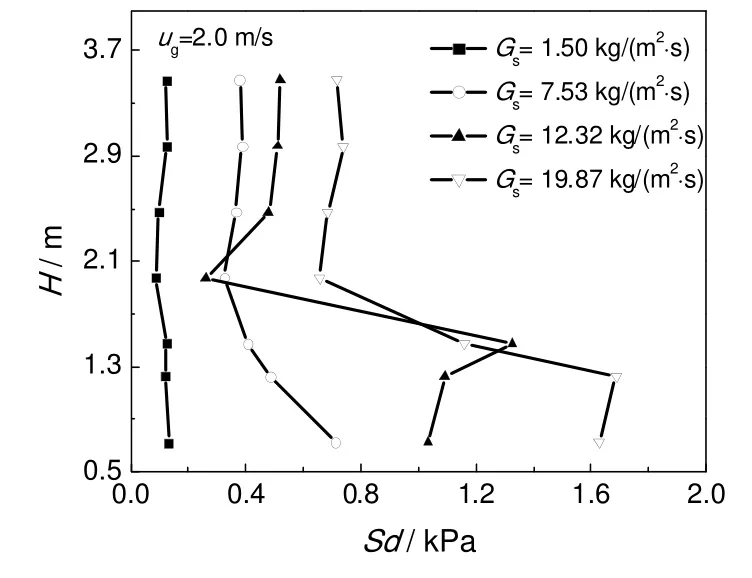
图3 标准偏差变化曲线Fig.3 Standard deviation of pressure fluctuations in the fluidized bed
2.3 功率谱分析
对图2中的压力信号进行功率谱分析得到图4的功率谱密度图,图中横坐标表示压力脉动的各种频率,纵坐标为各种脉动频率所对应的相对能量,能量最大点对应的频率称为主频,也就是信号主周期的倒数,表示此时压力信号由该频率起主导作用。由图4可以看出,压力脉动在低频区域有几个明显的峰值,表明该信号的压力脉动主要由这该频段(0.3~10 Hz)的脉动成分构成。随着颗粒质量流率的增加,主频所对应的能量峰值有所增加,说明脉动强度随着颗粒质量流率的增加而增大,这是由于随着循环速率的增大,流化床内部存在着主要以颗粒团聚物或颗粒群为主要流动特征的流动模式,这种颗粒群流经压力探头时带来的压力脉冲激发了幅值能量较大,而由于颗粒群的体积较大,其运动过程中,位移变化相对较慢,由此带来的压力脉动信号的主频也随之逐渐降低[由图4(a)所示的3~10 Hz降低至图4(b)所示的0.5 Hz 左右]。此外,由图4可以看出,不同高度处的压力脉动信号的主频基本相同,表征着压力波具有较好的传递性,床层之间的压力波衰减较弱。
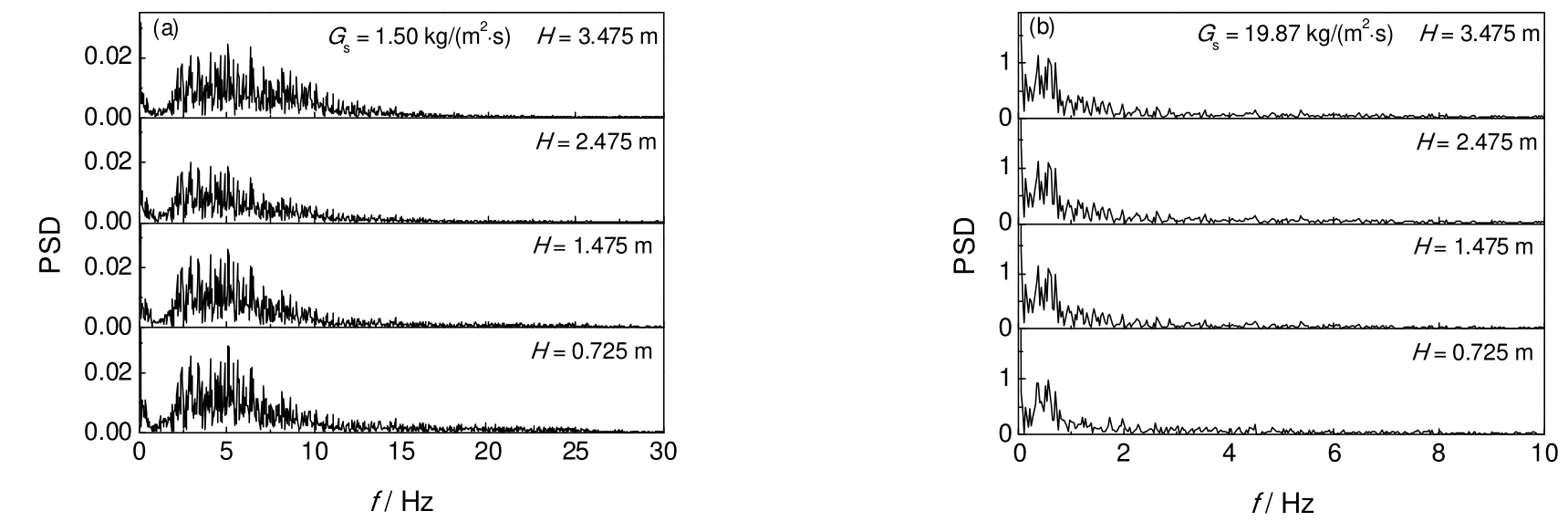
图4 压力脉动的功率谱密度Fig.4 Power spectral density of pressure fluctuations
2.4 多尺度小波分析
小波分解后的不同频段上的信息有着不同的物理意义,高频部分信号表明颗粒以非常稀的体积分数通过压力探头,颗粒在气体的作用下做高频湍动,信号频率广,但能量小,气固相互作用中气体起主导作用;低频部分信号主要是以高的颗粒体积分数或颗粒聚集体的形式通过压力探头,能量较高,固体颗粒在流动中占据主导地位。由图5可以看出,流化床内压力脉动的能量大多分布在低频区(尺度5~尺度9)。在低循环速率时,能量分布较为均匀,较为广地分布在尺度4~尺度8;而随着循环速率的增加,能量逐渐转变为集中在尺度9~尺度10 附近,这说明流态不同,压力信号的细节能量存在着较大的不同。同时,随着流化床高度的变化,该能量分布没有变化,这说明流化床内上下能量在频域上分布较为类似,都主要集中在低频区。

图5 多尺度能量特征值分布Fig.5 Multi-resolution energy distribution of pressure fluctuations
2.5 快速流化床内压力脉动形成的机理分析
快速流化床内的气固两相流动是一个不稳定的流动过程,主要体现在进料时存在的流量振荡、流动过程中颗粒的团聚与扩散、颗粒与颗粒以及气体与颗粒之间的碰撞等。根据2.4 节中的多尺度分析以及图5的内容可以认为压力脉动中存在的3 个尺度:大尺度(低频)、中尺度(中频)与小尺度(高频)3 个部分。小尺度信号是由气体与颗粒的湍动、颗粒碰撞、颗粒团聚物的形成与破裂等高频部分的信号组成,该尺度能量一般偏小;中尺度表明颗粒是以颗粒群或团聚物的形式流经压力探头的过程的体现,当颗粒团聚物靠近压力探头时,气体被压缩后,压力上升,当这颗粒团聚物离开压力探头时,气体释放,压力下降,由此引发的脉动现象,这种脉冲变化主要来自于不稳定进料所引起的较大的压力脉动,一般该尺度的能量占信号的主导作用;大尺度信号表明流化床床层的宏观稳定性,可以用来判断该处的压力是否异常,床层是否宏观稳定,当大尺度信号能量近似为0,表明流化床处于宏观稳定的流化状态,没有发生流动的噎噻或近似移动床的流动模式。
沿快速流化床的轴向上看,压力脉动的波形具有相似性,这是由于不稳定的进料引发的具有一定频率的周期性振荡。随着不稳定进料的波动,压力波沿着快速流化床床层往上传递,因而体现在图2中的轴向压力脉动具有一定的相似性,虽然在压力曲线能量的大小与局部的小尺度高频压力信号存在着变化,但是压力沿程波动的主频(即能量分率最大的压力分尺度)基本保持一致(见图4)。而随着颗粒循环速率的增加,进料的浓度也随之增加,使得压力脉动的强度也增大(见图3),而压力信号曲线的主频逐渐减小(见图4)。
3 结 论
快速流化床内的气固两相流是一种不稳定的流动,这种不稳定会造成气体与颗粒的压力脉动,本文在不同操作条件下测量的流化床内轴向动态压力的测量,经过分析后得到以下结论。
a)压力脉动的强度沿轴向由下至上逐渐衰减,且在循环速率较高时,底部的压力脉动标准偏差与顶部之间存在着明显的转折,这与流化床内部流场的轴向流态与稀密相分界面有关。
b)压力信号的主频随着颗粒质量流率的增加,其所对应的峰值(即脉动强度)有所增加,而主频的频率逐渐降低。不同高度处的压力脉动信号的主频基本相同,表明压力脉动在轴向上有着较高相关性。
c)压力脉动的小波多尺度分析表明压力脉动中存在大尺度(低频)、中尺度(中频)与小尺度(高频)3 个部分。小尺度信号主要体现在由于气体与颗粒的湍动、颗粒碰撞、颗粒团聚物的形成与破裂等高频部分的信号;中尺度信号主要捕获来自于不稳定进料所引起的较大的压力脉动;而宏观尺度信号主要表征整个流化系统的宏观稳定性,体现为低频与低幅值。
[1]赵贵兵, 陈纪忠, 阳永荣.流化床压力脉动信号时间延迟相关性 [J].化工学报, 2002, 53(12):1281-1286.Zhao Guibing, Chen Jizhong, Yang Yongrong.Delay time correlation of time of pressure fluctuations in bubbling fluidized bed [J].Journal of Chemical Industry and Engineering, 2002, 53(12):1281-1286.
[2]胡小康, 刘小成, 徐 俊, 等.循环流化床提升管内压力脉动特性 [J].化工学报, 2010, 61(4):825-831.Hu Xiaokang, Liu Xiaocheng, Xu Jun, et al.Characteristics of pressure fluctuations in CFB riser [J].Journal of Chemical Industry and Engineering, 2010, 61(4):825-831.
[3]张 毅, 魏耀东, 时铭显.气固循环流化床负压差下料立管的压力脉动特性 [J].化工学报, 2007, 58(6):1417-1420.Zhang Yi, Wei Yaodong, Shi Mingxian.[J].Characteristics of pressure fluctuation in standpipe at negative pressure gradient in circulating fluidized bed [J].Journal of Chemical Industry and Engineering, 2007, 58(6):1417-1420.
[4]Bi H T T.A critical review of the complex pressure fluctuation phenomenon in gas-solids fluidized beds [J].Chemical Engineering Science, 2007, 62(13):3473-3493.
[5]Fan L T, Ho T C, Hiraoka S, et al.Pressure fluctuations in a fluidized bed [J].AIChE Journal, 1981, 27(3):388-396.
[6]Kang W K, Sutherland J P, Osberg G L.Pressure fluctuations in a fluidized bed with and without screen cylindrical packings [J].Industrial &Engineering Chemistry Fundamentals, 1967, 6(4):499-504.
[7]Bi H T, Zhu J X.Static instability analysis of circulating fluidized beds and concept of high-density risers [J].AIChE Journal, 1993,39(8):1272-1280.
[8]Bi H T, Grace J R, Zhu J.Propagation of pressure waves and forced oscillations in gas-solid fluidized beds and their influence on diagnostics of local hydrodynamics [J].Powder Technology, 1995, 82(3):239-253.
[9]Johnsson F, Zijerveld R C, Schouten J C, et al.Characterization of fluidization regimes by time-series analysis of pressure fluctuations [J].International Journal of Multiphase Flow, 2000, 26(4):663-715.
[10]Punčochář M, Drahoš J.Origin of pressure fluctuations in fluidized beds [J].Chemical Engineering Science, 2005, 60(5):1193-1197.
[11]van der Schaaf J, Johnsson F, Schouten J C, et al.Fourier analysis of nonlinear pressure fluctuations in gas-solids flow in CFB risers-Observing solids structures and gas/particle turbulence [J].Chemical Engineering Science, 1999, 54(22):5541-5546.
[12]Yang T Y, Leu L P.Multiresolution analysis on identification and dynamics of clusters in a circulating fluidized bed [J].AIChE Journal,2009, 55(3):612-629.
[13]Yang T Y, Leu L P.Multi-resolution analysis of wavelet transform on pressure fluctuations in an L-valve [J].International Journal of Multiphase Flow, 2008, 34(6):567-579.
[14]Pence D V, Beasley D E, Riester J B.Deterministic chaotic behavior of heat transfer in gas fluidized beds [J].Journal of Heat Transfer,1995, 117(2):465-472.
[15]Bai D, Issangya A S, Grace J R.Characteristics of gas-fluidized beds in different flow regimes [J].Industrial &Engineering Chemistry Research, 1999, 38(3):803-811.

