稳健的条件概率约束匹配场处理

王 奇王英民 苟艳妮

(西北工业大学航海学院 西安 710072)

1 引言

匹配场处理技术能够成功地将水声信道的物理特性和传统的信号处理算法相结合，因此被广泛地用于对水下目标的被动定位和海洋环境声学参数反演等方面，其主要方法是采用声传播模型[1](如简正波模型、抛物方程模型、射线模型等)构建观测海域的拷贝场向量，并与测量场数据进行“匹配”相关来估计声源及信道信息[2,3]。匹配场处理主要分为两大类：一是线性匹配场处理器 CMFP[4](Conventional MFP)，又称为Bartlett处理器；二是自适应匹配场处理器AMFP(Adaptive MFP)，具有代表性的是最小方差无失真响应(MVDR)处理器[5,6]。Bartlett具有较好的稳健性，但旁瓣较高，主旁瓣较难区分。MVDR提供了理论上的最高阵增益，而且具有优异的旁瓣抑制特性，但环境失配时性能急剧下降。

为了能够获得较高阵增益的同时提高算法的稳健性，国内外学者在MVDR的基础上提出了许多宽容的AMFP处理方法[710]-，具有代表性的如：邻域位置约束匹配场处理器 MV-NLC(Neighborhood Location Constraints)、最小方差环境扰动约束匹配场处理器 MV-EPC(Environmental Perturbation Constraints)和扇区聚焦方法 SF(Sector Focusing)等。

MV-NLC以小范围的位置约束来保护主瓣并克服环境失配，但算法的有效性依赖于环境失配与声源位置变化的相似程度，等声速波导中海深误差常常对应声源位置变化，但其它类型的环境失配如声速剖面与地声参数失配则并无此对应关系，此时算法失效；MV-EPC利用环境参数扰动范围内拷贝信号相关矩阵的一阶和二阶统计特性对主瓣进行保护，算法的运算量很大。SF方法用一定区域内的多个拷贝场向量构造了一个投影矩阵，然后利用投影矩阵消去了噪声及环境失配对匹配场处理的影响，但该算法对扇区大小的选择较难。除此之外还有一些其他稳健的AMFP算法，如降阶的MV-EPC、环境扰动约束的SF等。

为了能够提高AMFP算法的稳健性，本文利用贝叶斯准则推导出了位置参数的后验概率估计，然后用后验概率密度对 AMFP进行约束，以此为AMFP提供一定程度的主瓣保护和旁瓣抑制能力，在失配环境下获得了较好的宽容性。最后使用1993年 NRL(Naval Research Laboratory)研讨会[11]上公布的典型失配环境“genlmis”的仿真数据验证了算法的性能。

2 不确定环境下稳健的匹配场处理

2.1 数据模型

设声源频率为ω，位置参数向量为m(包含距离r和深度z)，声传播信道参数集为ψ，则N元垂直线列阵接收的声压向量在频域可表示为[12]

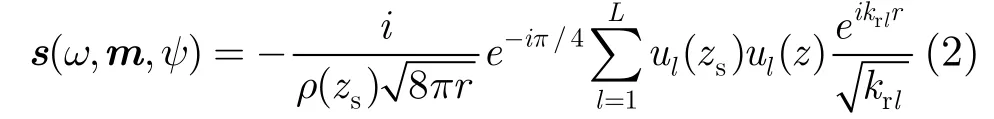
2.2 MVDR匹配场处理器

通常匹配场处理器的输出 ()Bm 由采样协方差矩阵R和权向量w组成。

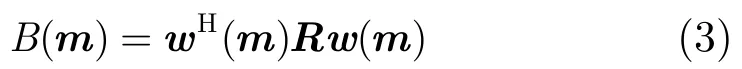
对于式(1)的数据模型，采样协方差矩阵R可表示成K个频域快拍的最大似然估计：

为了抑制旁瓣提高分辨率，文献[5,14,15]等介绍了一种自适应匹配场处理方法，称为最小方差无失真响应(MVDR)处理器，其数学表述为

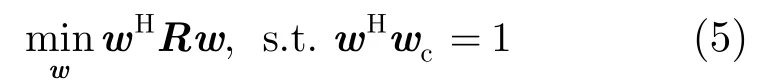
用拉格朗日乘子法解此最优化问题可求得MVDR的权向量和输出功率为

MVDR的阵增益及主旁瓣性能优于Bartlett处理器，但当水声环境具有扰动时，特别是信噪比较大时，自适应匹配场极易出现严重的“目标自抑制”现象，因此稳健性远不如Bartlett处理器。

2.3 条件概率约束的自适应匹配场处理器

根据贝叶斯准则声源位置参数的后验概率密度函数可表示为[16]

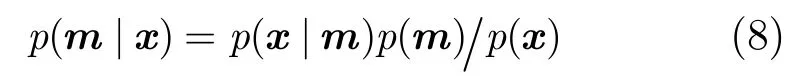
对式(1)所示的数据模型，由于N元垂直线列阵各阵元的噪声是独立同分布的加性高斯白噪声，则可以得到条件概率密度，即似然函数：

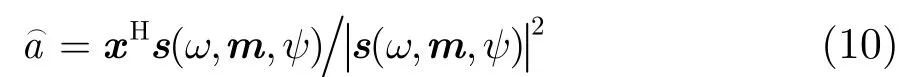
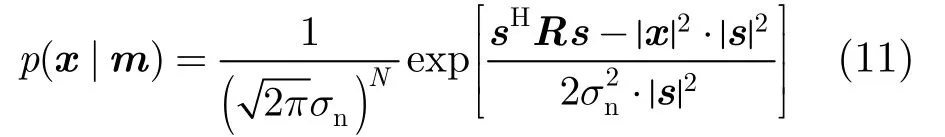
根据贝叶斯准则后验概率密度函数可写为

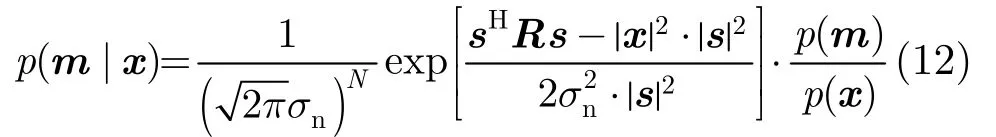
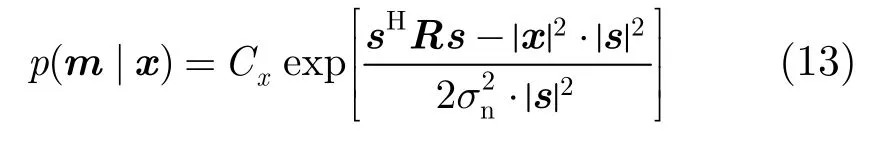
得到位置参数的后验概率密度函数后，可以构造如式(14)的匹配场处理器，称为条件概率约束的匹配场处理器(MFP-CPC)。

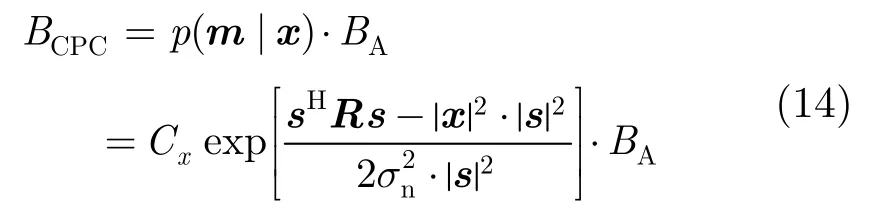
其中，AB 为AMFP的输出功率。从MFP-CPC的表达式可看出，该处理器充分利用了环境先验信息，把贝叶斯准则引入到了算法中，是一种数据驱动和模基相结合的方法；而且算法以 AMFP为基本单元，具有通用的表达式。本文后续的仿真中使用经典的 MVDR 作为式(14)的AB ，即使用式(7)的作为式(14)中的。

3 仿真分析

3.1 仿真模型

1993年5月NRL的研讨会上公布了几种典型的浅海环境模型和仿真数据供研究者使用[11]，其目的是为了能够客观公正地对比不同环境下匹配场定位及反演算法的性能。其中“genlmis”主要用来验证在环境参数失配及存在有色噪声情况下算法的性能，是一种失配比较严重的仿真案例，本文在此基础上进行仿真分析。

仿真中使用一个包含 20个阵元的垂直线列阵接收声源辐射的信号，声源频率为250 Hz。第1个阵元的深度为5 m，最后一个阵元的深度是 100 m，阵元间距为 5 m。使用Kraken简正波模型计算拷贝场向量，观测海域的距离范围为：5～10 km，步长20 m；深度范围为：1～100 m，步长1 m。

图1是“genlmis”的真实环境参数模型，即使用该环境模型构造测量场。此环境下分别存在3种声源：(1)声源位于(6.2 km, 92 m)，信噪比为40 dB；(2)声源位于(9.0 km, 74 m)，信噪比为10 dB；(3)声源位于(7.2 km, 16 m)，信噪比为-5 dB。

3.2 无失配时的仿真结果

假设声源位于(9.0 km, 74 m)，信噪比为10 dB，可以精确得知环境参数模型如图1所示，分别使用Bartlett, MVDR和MFP-CPC进行匹配场处理，得到如图2所示的定位切片图，从图2的结果可知3种处理器都能够准确定位目标，且 MVDR和MFP-CPC具有更窄的主瓣和更低的旁瓣。当阵元数N为20且完全匹配时，匹配场处理器的理论输出功率为，从图2(a)和图2(c)可看出，对于Bartlett和MVDR，其在(9.0 km, 74 m)处的功率近似为13 dB，和理论值一致。但MFP-CPC的输出功率远小于前二者，主要原因是后验概率对匹配场处理器的输出产生了影响。

图1 GENLMIS真实环境模型

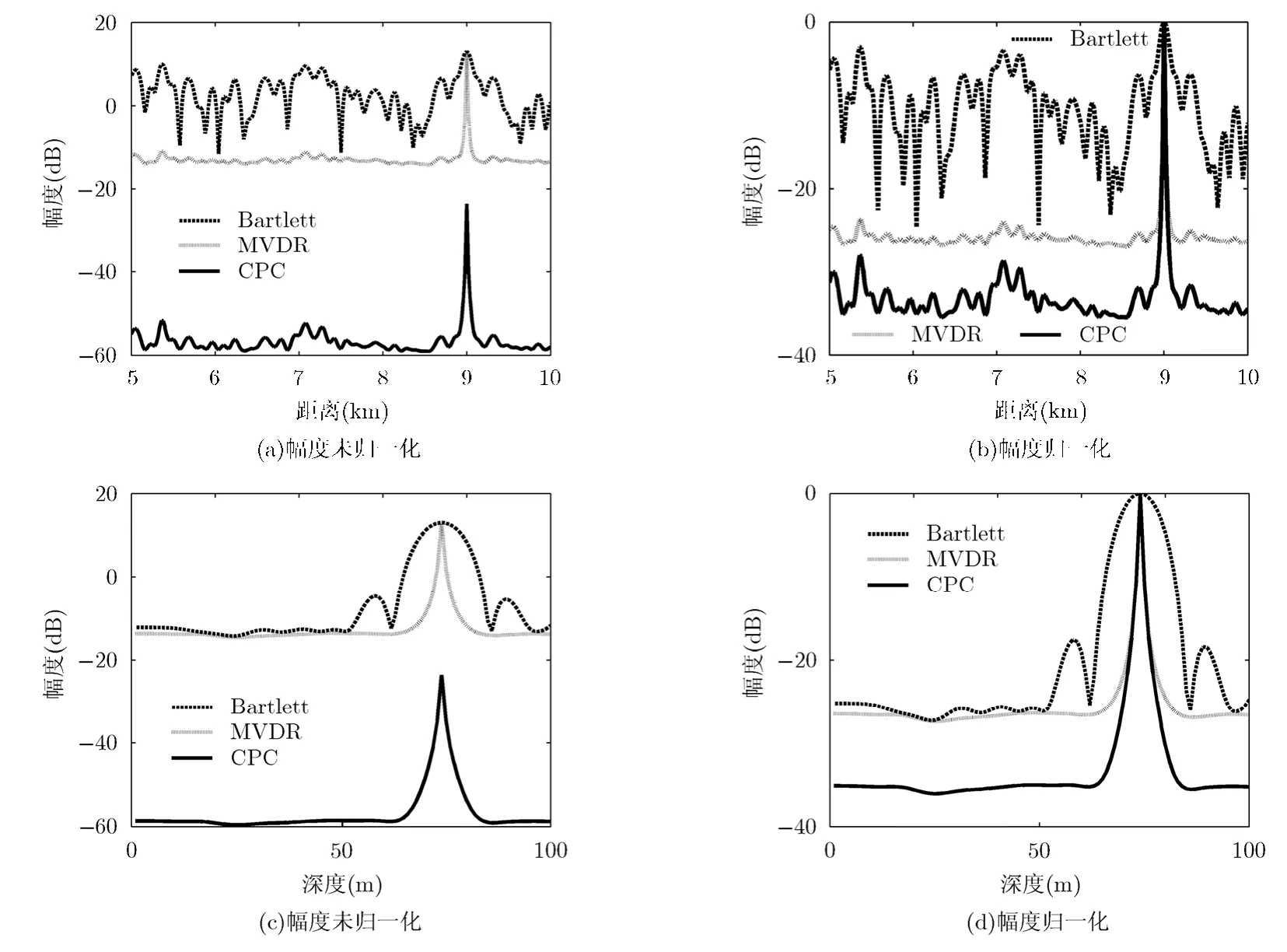
图2 3种匹配场处理器的定位切片图

图2(b)和图2(d)画出了幅度归一化后3种处理器的对比结果，从图2可看出MFP-CPC和MVDR的主瓣完全重合，二者在距离方向的-3 dB主瓣宽度约20 m，在深度方向的-3 dB主瓣宽度约1.5m，而Bartlett相应的主瓣宽度分别约为100 m和7 m。从图 2(b)可看出，距离方向上 MVDR最高的旁瓣比Bartlett低约35 dB，而MFP-CPC最高的旁瓣比MVDR又低约6 dB；从图2(d)可知，深度方向上图中的显示尺度已经无法辨别 MVDR和MFP-CPC的旁瓣，其旁瓣已经湮没在背景中，MVDR的背景比Bartlett的最高旁瓣低约24 dB，而MFP-CPC的背景又比MVDR低约8 dB。

从环境参数精确已知时的仿真结果可看出，MFP-CPC的定位性能明显优于Bartlett，其主瓣宽度和MVDR相似，且MFP-CPC的旁瓣比MVDR低约6 dB，背景低约8 dB。

3.3 参数失配时的仿真结果

测量场仍然由图1的环境模型计算，假设地声环境参数存在不确定性，无法得出图1环境参数的真实值，只能根据经验得到如图3所示的环境参数先验信息。与图1所示的真实环境模型对比可知，海面声速失配-0.1 m/s，海底声速失配-1.3 m/s，基底上表面声速失配-26 m/s，基底中部声速失配-56 m/s，基底下部声速失配-56 m/s，基底衰减失配-0.01 dB/λ，基底密度失配-0.01 g/cm3，海水深度失配4.9 m，除此之外“genlmis”的测量场数据中还存在有色噪声。

图4是genlmis环境参数失配模型下，3种匹配场处理器对3.1节中的3种声源的定位模糊度平面。按照处理器的类型分类：图4(a1)-图4(a3)是Bartlett的定位结果；图4(b1)-图4(b3)是MVDR的定位结果；图4(c1)-图4(c3)是MFP-CPC的定位结果。按照声源分类：图4(a1), 4(b1), 4(c1)对应信噪比为40 dB的声源 1；图 4(a2), 4(b2), 4(c2)对应信噪比为 10 dB的声源2；图4(a3), 4(b3), 4(c3)对应信噪比为10 dB的声源 3。图 4每幅子图的小矩形框内部的主峰是匹配场处理器估计的声源位置，真实声源位置见3.1节的描述。

当信噪比为 40 dB和 10 dB时，Bartlett和MFP-CPC都能够正确定位，但Bartlett的模糊平面中幅值接近主峰的旁瓣很多，图4(a1)中(6.2 km,92 m)处的主峰和(8.2 km, 92 m)处的最大旁瓣幅度相差小于2 dB，图4(a2)中(9.1 km, 72 m)处的主峰和(7.2 km, 70 m)处的最大旁瓣幅度相差小于1 dB，很难区分主旁瓣。而图4(c1)中MFP-CPC的主峰比最高旁瓣高约6 dB；图4(c2)中最高旁瓣位置变为(7.7 km, 16 m)，和图4(a2)中的最高旁瓣位置不一致，从图4(b2)中可看出是由于受到MVDR的影响，然而图4(c2)中(9.1 km, 71 m)处的主峰仍比最高旁瓣高约3 dB，相比之下MFP-CPC具有明显的旁瓣压缩性能。在这两种信噪比情况下，MVDR出现严重的“自抑制”现象，在海水表面处出现多个峰值，说明MVDR对失配最敏感，但较好的一点是在真实声源位置处还是可以看到峰值。当信噪比为-5 dB时，环境失配及有色噪声的影响最明显，此时3种匹配场处理器全部失效，其中MVDR定位的虚假目标也比较模糊。相比之下Bartlett和MFP-CPC虽然只是在(6.5 km, 16 m)附近出现了一个虚假的峰值，但二者虚假目标都比较清楚。对比Bartlett和MFP-CPC的处理结果还可看出，即使是在失配较严重的情况下，二者在目标附近的模糊度图也具有一定的相似度，即二者具有类似的稳健性。

4 结束语

匹配场处理时由于先验环境信息的不确定，使得构建的环境模型与真实环境极易出现失配，最终导致匹配场处理的性能严重下降，这种情况对自适应匹配场处理尤为明显。针对这种情况，本文提出了一种条件概率约束的匹配场处理方法。算法利用垂线阵接收的测量场数据计算出了位置参数的后验概率密度，在此基础上为自适应匹配场处理器提供了主瓣保护和旁瓣抑制特性。环境参数精确已知时的仿真结果表明：MFP-CPC的主瓣宽度和MVDR一致，旁瓣压缩性能比MVDR高了约6～8 dB。典型失配环境下的定位结果证明：MFP-CPC具有和Bartlett相类似的稳健性。另外，条件概率约束算法实现相对简单且表达式具有通用性和一般性，可以使用其他自适应算法来替换掉该算法中的自适应单元，从而进一步提高算法的稳健性。但该算法在计算后验概率估计时仍需要用到先验环境信息，因此失配问题同样存在，只是和该算法中用到的自适应匹配场处理器相比，稳健性有所提高。

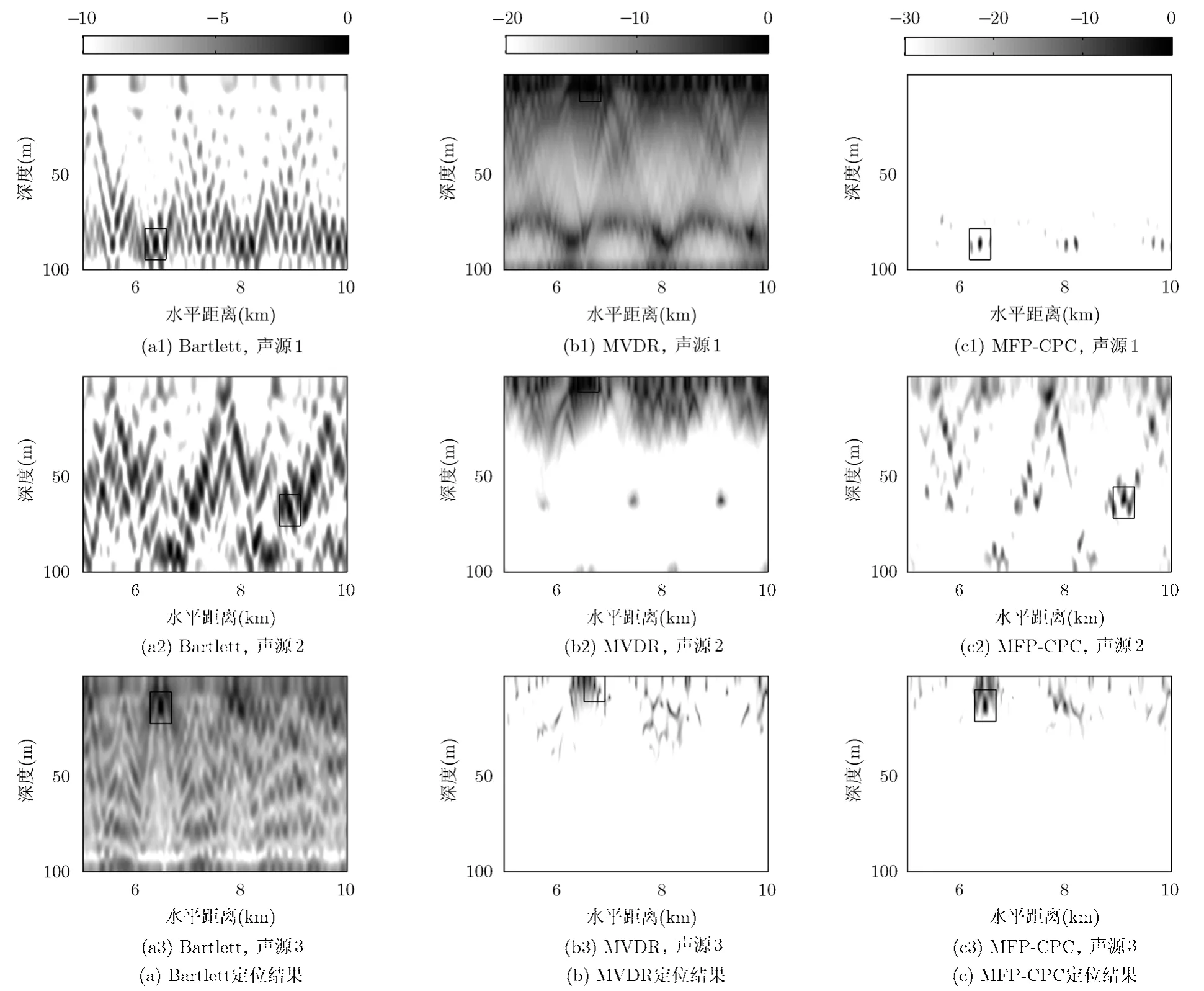
图4 genlmis环境模型下3种匹配场处理器的定位结果

[1] Porter M B. The Kraken normal mode program[R]. La Spezia Italy, 1992.

[2] Baggeroer A B, Kuperman W A, and Mikhalevsky P N. An overview of matched field methods in ocean acoustics[J].IEEE Journal of Oceanic Engineering, 1993, 18(4): 401-424.

[3] 游伟, 何子述, 胡进峰. 基于匹配场处理的天波雷达高度估计算法[J]. 电子与信息学报, 2013, 35(2): 401-405.You Wei, He Zi-shu, and Hu Jin-feng. Skywave radar altitude estimation algorithm based on matched-field processing[J].Journal of Electronics ＆amp; Information Technology, 2013, 35(2):401-405.

[4] Mantzel W, Romberg J, and Sabra K. Compressive matched-field processing[J]. The Journal of the Acoustical Society of America, 2012, 132(1): 90-102.

[5] Shorey J A, Nolte L W, and Krolik J L. Computationally efficient Monte Carlo estimation algorithms for matched field processing in uncertain ocean environments[J]. Journal of Computational Acoustics, 1994, 2(3): 285-314.

[6] Singh V, Knisely K E, Yönak S H, et al. Non-line-of-sight sound source localization using matched-field processinga[J].The Journal of the Acoustical Society of America, 2012,131(1): 292-302.

[7] Teyan C, Chunshan L, and Zakharov Y V. Source localization using matched-phase matched-field processing with phase descent search[J]. IEEE Journal of Oceanic Engineering, 2012,37(2): 261-270.

[8] Zhuan X, Wen X, and Xianyi G. Robust matched field processing for source localization using convex optimization[C]. OCEANS’09 IEEE Bremen: Balancing Technology with Future Needs, Bremen Germany, 2009: 1-5.

[9] Schmidt H, Baggeroer A B, Kuperman W A, et al.Environmentally tolerant beamforming for high-resolution matched field processing: deterministic mismatch[J]. The Journal of the Acoustical Society of America, 1990, 88(4):1851-1862.

[10] Chandler H A, Feuillade C, and Smith G B. Sector-focused processing for stabilized resolution of multiple acoustic sources[J]. The Journal of the Acoustical Society of America,1995, 97(4): 2159-2172.

[11] Porter M B, and Tolstoy A. The matched field processing benchmark problems[J]. Journal of Computational Acoustics,1994, 2(3): 161-185.

[12] 刘凤霞, 潘翔, 宫先仪. 螺旋线阵匹配场三维定位[J]. 浙江大学学报(工学版), 2013, 47(1): 62-69, 76.Liu Feng-xia, Pan Xiang, and Gong Xian-yi. Matched-field three-dimensional source localization using spiral line array[J].Journal of Zhejiang University (Engineering Science), 2013,47(1): 62-69, 76.

[13] Yang K, Zhang T, and Ma Y. Matched-field processing using time-reversal concept in a range-dependent environment[J].The Journal of the Acoustical Society of America, 2012,131(4): 3239.

[14] Krolik J L. Matched-field minimum variance beamforming in a random ocean channel[J]. The Journal of the Acoustical Society of America, 1992, 92(3): 1408-1419.

[15] Lee N, Zurk L M, and Ward J. Evaluation of reduced-rank,adaptive matched field processing algorithms for passive sonar detection in a shallow-water environment[C].Conference Record of the Asilomar Conference on Signals,Systems and Computers. United States, 1999, 2: 876-880.

[16] Bretthorst G L. The maximum entropy method of moments and Bayesian probability theory[C]. 32nd International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Garching, Germany,2012: 3-15.