自适应Alpha-beta修正的线谱检测后置处理方法

戴文舒陈新华孙长瑜余华兵

①(中国科学院声学研究所 北京 100190)②(中国科学院大学 北京 100190)

1 引言

水下目标辐射噪声中有丰富的单频分量，特别是低频段，通常线谱谱级要比连续谱高出 10～25 dB。在被动声呐信号处理中，常规宽带能量积分的信号检测方法已远远不能满足信噪比低、复杂声场环境下的检测问题。利用较高强度和稳定度的线谱已证明能够提高目标的检测性能和抗干扰能力，但存在目标辐射噪声中线谱频带未知，搜索麻烦的问题。因此宽带高斯噪声背景下，利用目标辐射噪声中线谱实现目标检测需要分频带融合，目前主要有基于线谱方位稳定性的宽带融合方法和频率稳定性的宽带融合方法，而且积累了一定的理论基础。文献[1]研究了频率域分析和时间域频率分析特征值之间的关系，即瞬时频率和有效带宽的关系；提出了具有矩形包络的单频信号时间域角度瞬时频率序列的二阶中心矩即瞬时频率方差等于频率域角度频谱的有效带宽。频域有效带宽越大，时域瞬时频率方差越大。文献[2]针对同一问题，提出了单频叠加带限干扰信号的时间域瞬时频率序列二阶中心矩和频率域频谱有效带宽的关系。证明当单频信号为零时，频率方差为带限信号的有效带宽；当只存在单频信号时，频率方差为 0；当存在多线谱分量时，频率方差会变大；单频信号的瞬时频率方差与信号的绝对幅度无关，只是信噪比的函数，信噪比降低时，瞬时频率方差变大。文献[3]基于此理论，提出了常规波束形成(CBF)频率方差线谱检测器，即在频率域用每个方位的波束谱峰值频率方差对 CBF输出的方位谱进行加权来得到线谱目标的方位。同时验证了其优越的抗干扰能力。另外也有其他相关文献从方位角度出发[4]，如方位稳定性算法，原理类似。

以上提出的宽带融合检测算法都是在信噪比相对较高时性能良好。但随着目标辐射噪声级日益降低，信噪比变得很低，无论是瞬时频率序列方差还是方位方差都会变得很大，使这些融合算法失效。因此对瞬时频率序列或方位序列进行修正很有必要。针对频率稳定性算法，已有一些方法对频率序列进行后置数据处理，例如多项式拟合[5]，Kalman滤波[6]，常规Alpha-beta滤波器等。多项式拟合法系数恒定而常规Alpha-beta方法增益矩阵恒定[7]，估计的频率序列均值误差大；Kalman滤波极容易受野值影响[8]，而且先验知识未知时，拟合后的序列和真实值误差仍然很大，从而求得的频率方差依旧很大。本文根据迹迹相关原理，基于统计时间内，线谱信噪比足够大而且稳定的假设[9]，对每个方位的波束谱多次统计结果进行求和，获得功率谱-频率曲线，并作为Alpha-beta滤波器的增益选取依据。功率谱大的频率观测值增益大，在递推过程中新息所占的权重大；功率谱小的频率观测值增益小，在递推中预测所占的权重大，从而对频率序列进行拟合，进行频率方差修正。仿真和实验数据验证了采用自适应增益的Alpha-beta修正频率峰值序列后的方位频率方差比已有算法估计的结果更准确，因此求得的方位谱加权因子也更有效，从而改善了频率稳定性算法的检测效果。

2 算法原理

2.1 Alpha-beta滤波器[10]

Kalman滤波是一组以递推关系给出的随机系统状态最优线性滤波算法，其预测过程的原理是通过现时观测值修正来得到最佳预测值，根据观测的数据自动改变它的系数并保证其同下一刻的真实值的均方误差最小。当递推充分多的步数后，增益矩阵将趋于常数矩阵。Alpha-beta滤波器使用该常数增益，它的增益参数为α, β，在本质、结构和性能上与Kalman相似，却大大降低了其计算复杂度。

线性Kalman滤波用状态转移和观测方程来描述信号模型。

时间更新：

测量值更新：

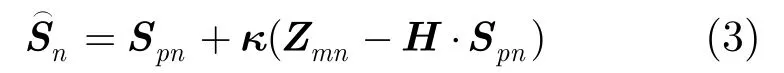
2.2 方位谱峰值频率序列

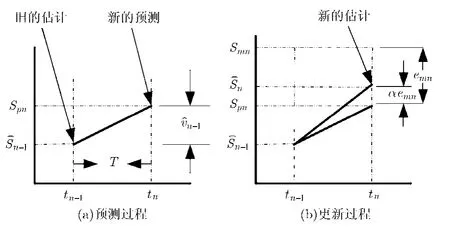
图1 Alpha-beta滤波原理

对水下目标检测通常有宽带能量积分和高强度稳定线谱检测，线谱检测的处理增益10lg2BT大于能量检测器的处理增益5lgBT[4]，其中BT为时间带宽积。但目标辐射信号中的线谱频率是未知的，因此为了利用最大输入信噪比检测信号，需要对频带内的每个频率单元进行处理，每个频率单元对应一个波束输出，需要对每个频率单元的结果循环分析判断才能得到对目标的正确检测，在工程中是不可取的。线列阵频率方差检测算法是利用线谱的高信噪比和足够大的处理增益，通过统计方位谱峰值频率序列方差，简化结果输出的一种宽带融合算法，其具体步骤如下：

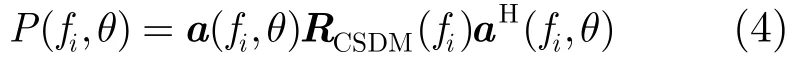
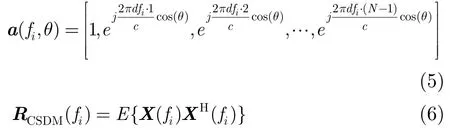
(4)在设定的统计时间T内，更新接收信号，重复进行步骤(1)～步骤(3)。统计 T 个频率峰值序列的方差，记做。

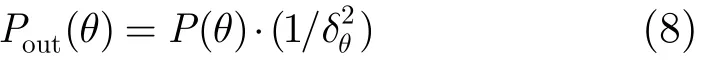
2.3 自适应增益k

分析 2.2节中频率方差检测的基本原理及引言中相关理论，步骤(4)中对某方位下频率峰值方差统计时，当信噪比下降时，统计方差增大，会导致目标检测能力下降。根据人眼视觉特性，文献[11]研究认为：显示行数每增加一倍，可以降低检测信噪比2.2 dB左右。采用文献[12]中3.2节目标运动估计的方法，得到若声呐作用距离20 km，目标以最大航速 30 kn从i号波束主极大方向运动以最近距离运动到波束主极大方向需要45 s。声呐行扫描周期小于0.5 s。因此，在求取频率峰值序列时，设定统计时间，可以认为目标方位变化很慢，在一个波束角度内。

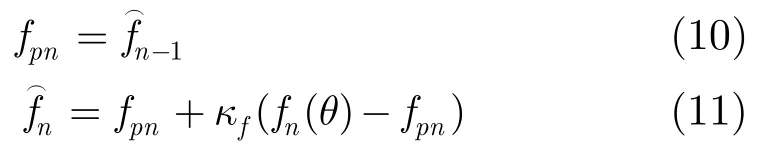
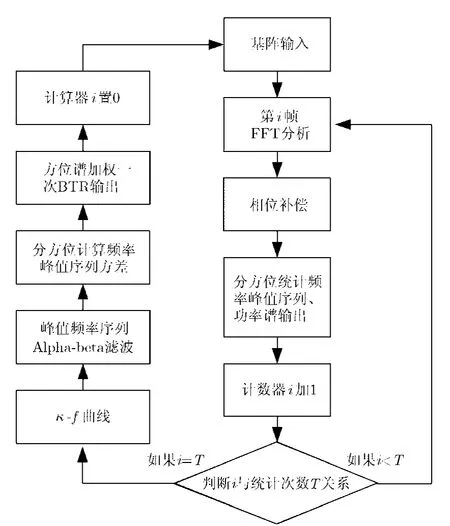
图2 自适应Alpha-beta后置拟合线谱检测算法一次波束输出流程图

2.4 目标方位输出值和其他方位输出值关系

根据引言部分，频域有效带宽越大，时域瞬时频率方差越大。当单频信号为0时，频率方差为带限信号的有效带宽；当只存在单频信号时，频率方差为0；设预成方位的最小和最大单元为1θ,Lθ，目标线谱位于0θ，共进行T帧的信号统计。在方位下有线谱信号，频率的实际估计值最小和最大值分别为，其他方位θ下，频率的实际估计值均匀分布在有效带宽内。每个方位下的频率序列方差为

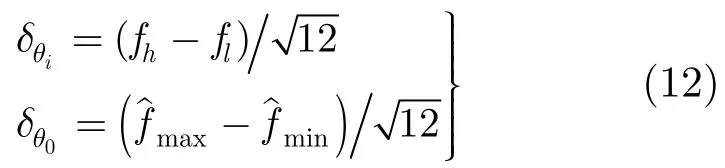
3 自适应增益 Alpha-beta后置处理算法仿真

假设基阵阵元数为32，阵间距为8 m，两目标相对于水平长线阵方位为60°和100°，一宽带干扰方位为130°，目标1辐射信号包括高斯带限白噪声和线谱成分，滤波器带宽为10～200 Hz，线谱频率为60 Hz。目标2辐射信号只包括100 Hz线谱。线谱谱级与白噪声平均谱级比为13 dB。

归一化曲线和频率序列滤波

目标辐射噪声和海洋背景噪声信噪比为-25 dB。宽带干扰与海洋背景噪声信噪比为-20 dB。则基阵接收信号的线谱谱级比背景噪声谱级低12 dB，比宽带干扰谱级高8 dB。

图3是计算得到的线谱方位100°时和非线谱方位150°的归一化曲线。可见线谱方位时，当观测的频率序列偏离 100 Hz，增益κ小，式(11)中新息所占的比重低，估计值主要由预测值决定，这就要求初始值选取准确，2.3节中对初值的处理也是合理的。而150°方位下的归一化曲线决定了递推公式中新息的比重较大，估计值主要由观测值决定。

图 4为线谱方位 100°时未拟合的频率峰值序列。图5是对图4进行滤波后的估计结果，可见线谱方位下的频率序列在后置处理后的方差变小，由此估计结果计算得到的方差权值提取效果更好。

3.2 算法仿真

目标辐射噪声和海洋背景噪声信噪比降为-30 dB。宽带干扰与海洋背景噪声信噪比为-25 dB。则基阵接收信号的线谱谱级比背景噪声谱级低17 dB，比宽带干扰谱级高8 dB。统计时间100 s，一次处理1 s数据，方位历程时间5000 s。分别采用常规能量积分、频率方差线谱检测算法、常规恒增益Alpha-beta后置滤波和自适应增益Alpha-beta后置滤波后的线谱检测算法。仿真结果如图6～图10所示。

从图6中统计后的一次方位历程图(BTR)结果可以看出，宽带干扰存在下，常规能量积分只能区分出130°的宽带目标，60°的宽带加线谱目标。而100°的线谱信号由于信噪比为-39.9 dB(13-10⋅lg190-30)，因此被宽带功率谱所淹没；而采用频率方差线谱检测器由于统计各次的频率序列的方差相近，对方位谱输出加权后丢失目标；采用后置滤波后的线谱检测器能实现所有含线谱目标(60 Hz, 100 Hz)的检测。

图7是对图6中常规能量积分进行5000 s的BTR结果，可以看出，丢失了100 Hz的弱线谱目标。图8中是图6中常规频率方差线谱检测器5000 s的BTR结果，可以看出，由于方差的随机性使目标丢失。

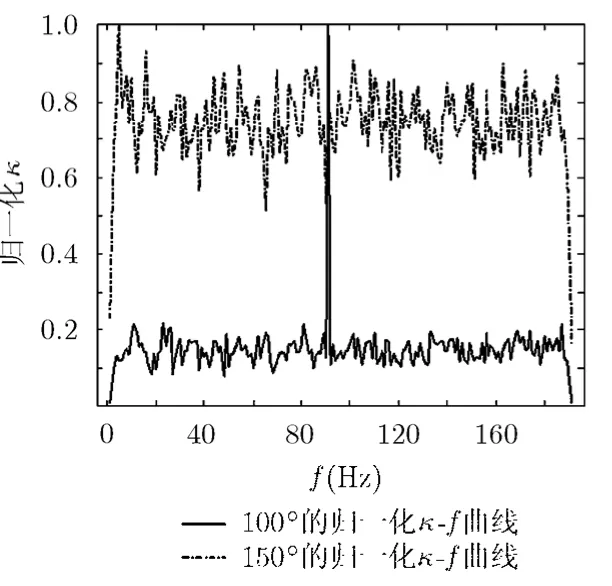
图3 线谱方位100°和非线谱方位150°下计算的κ-f归一化曲线

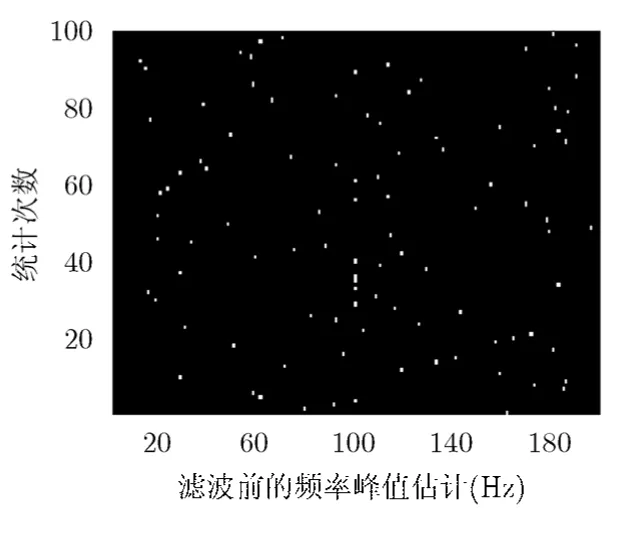
图4 线谱方位100°时未 拟合的频率峰值序列

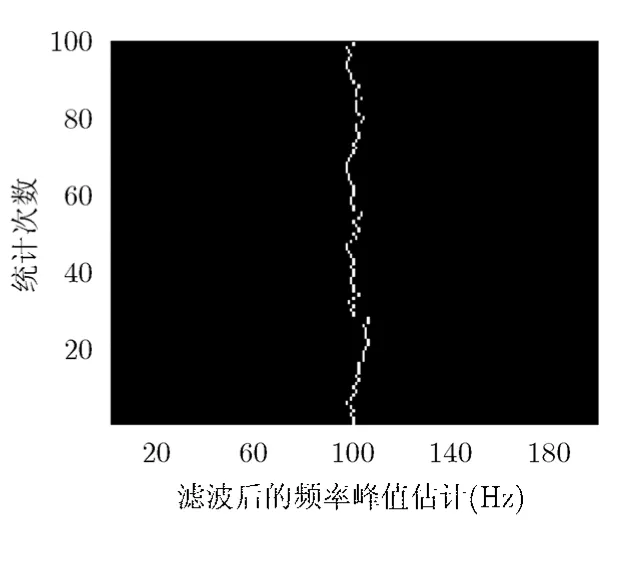
图5 线谱方位100°时拟合后 的频率峰值估值序列

图9是采用恒增益Alpha-beta滤波线谱检测算法进行5000 s的BTR结果，Kalman滤波的稳态情况即恒增益下Alpha-beta滤波并未改善由于信噪比降低后方差变大导致弱线谱目标丢失的检测结果。图10是图6中自适应增益Alpha-beta后置拟合线谱检测算法进行5000 s的BTR结果，可以正确判断60°和100°的线谱目标。

4 实验数据处理

将本文算法用在海试长线阵中去，实验采用32元阵接收信号，阵端方向设为0°，水下运动目标相对于长线阵大约在 100°左右，150°附近有一强线谱目标，分别采用常规能量积分和后置处理线谱检测方法，一次方位历程估计结果如图11所示，可以看出后置处理后的方位历程图在 100°能明显发现目标，而且干扰背景被压低。

5 结束语

自适应增益 Alpha-beta 后置滤波算法适用在信噪比很低的情况。当多次能量积分累加都无法检测到目标，线谱方位频率方差和其他方位频率方差接近的情况下，本文通过构造自适应增益，该增益是频率的函数，来对对应方位下统计后的观测频率进行拟合，大增益时频率观测在递推中占的比重大，小增益时预测频率在递推中起主要作用，用各方位拟合后的频率计算方差，对方位谱进行加权输出。仿真和实验结果验证了该后置处理算法能有效提取目标线谱，改善检测效果，有很好的工程应用前景。

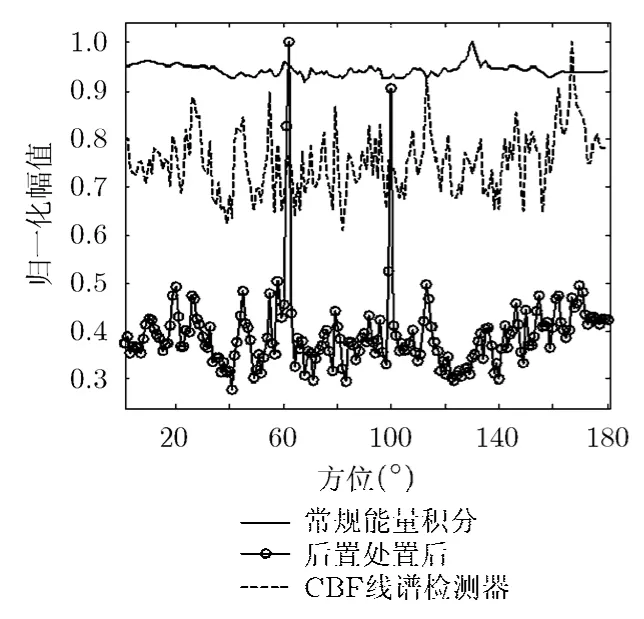
图6 常规能量积分、线谱检测及后置处理后一次波束输出

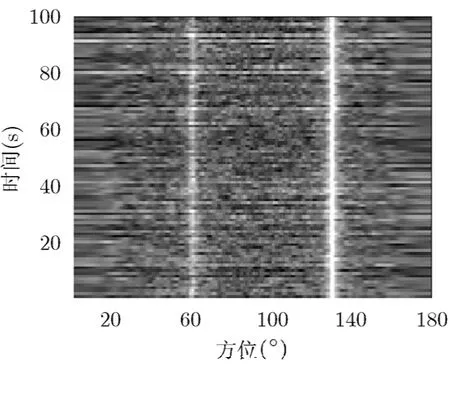
图7 常规能量检测的 方位历程图

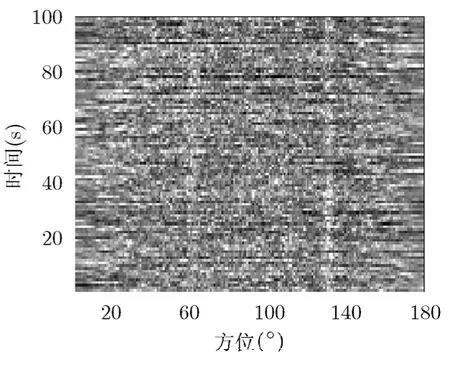
图8 未经后置处理的线谱 检测方位历程图

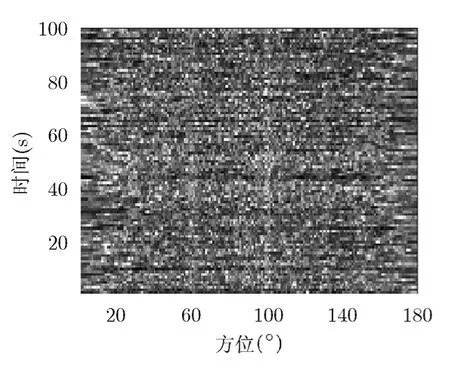
图9 常规恒增益Alpha-beta滤波后置拟合后的线谱检测方位历程图

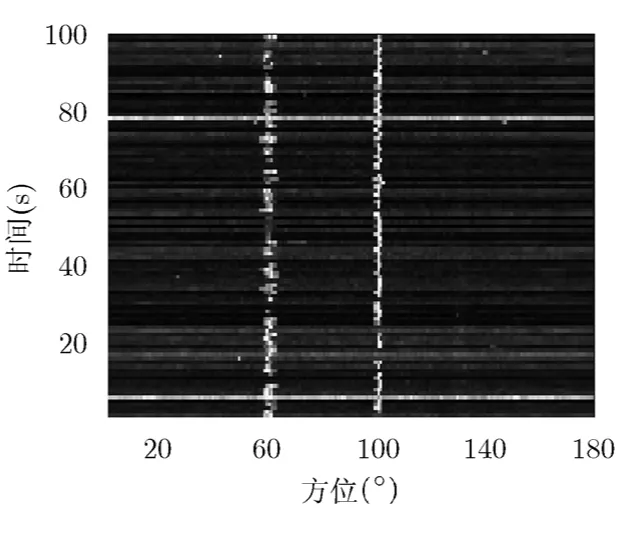
图10 经自适应增益Alpha-beta滤波后 置拟合后的线谱检测方位历程图

图11 4种弱线谱检测 算法对比

[1] 梁国龙, 惠俊英, 常明. 瞬时频率序列及其低阶矩的应用研究[J]. 声学学报, 1995, 24(4): 280-288.Liang Guo-long, Hui Jun-ying, and Chang Ming. Study on applications of transient frequency sequence and its moments[J]. Acta Acustica, 1995, 24(4): 280-288.

[2] 梁国龙, 惠俊英. 瞬时频率方差检测器及其性能评价[J]. 声学学报, 1999, 24(2): 183-190.Liang Guo-long and Hui Jun-ying. Variance of instantaneousfrequency detector and its performance evaluation[J]. Acta Acustica, 1999, 24(2): 183-190.

[3] 陈阳, 王自娟, 朱代柱, 等. 一种基于瞬时频率方差加权的线谱目标检测方法[J]. 声学学报, 2010, 35(1): 76-80.Chen Yang, Wang Zi-juan, Zhu Dai-zhu, et al.. A detecting method for line-spectrum target based on variance-offrequency weight[J]. Acta Acustica, 2010, 35(1): 76-80.

[4] 陈新华, 鲍习中, 李启虎, 等. 水下声信号未知频率的目标检测方法研究[J]. 兵工学报, 2012, 33(4): 471-475.Chen Xin-hua, Bao Xi-zhong, Li Qi-hu, et al.. Research on detection of underwater acoustic signal with unknown frequency[J]. Acta Armamentrii, 2012, 33(4): 471-475.

[5] 陈新华, 余华兵, 等. 一种水声目标信号检测和识别方法[P].中国专利, 101738611A, 2010.Chen Xin-hua, Yu Hua-bing, et al.. A detective and classify method for underwater acoustic signal[P]. Patent of China,101738611A, 2010.

[6] 沈笑慧, 张健, 何熊熊. 基于接收信号强度指示加权融合的定位算法[J]. 华侨大学学报(自然科学版), 2012, 33(6): 635-639.Shen Xiao-hui, Zhang Jian, and He Xiong-xiong. Localization algorithm based on received signal strength indication weighted fusion[J]. Journal of Huaqiao University (Natural Science), 2012, 33(6): 635-639.

[7] Kawase T, Tsurunosono H, Ehara N, et al.. An adaptive-gain alpha-beta tracker combined with circular prediction for maneuvering target tracking[C]. Proceedings of IEEE Region 10 Annual Conference TENCON,96, Speech and Image Technologies for Computing and Telecommunications, Japan,1997, 2: 795-798.

[8] 戴文舒, 陈新华, 孙长瑜, 等. 等价权修正的 Kalman抗野值滤波算法[J]. 应用声学, 2013, 32(5): 409-412.Dai Wen-shu, Chen Xin-hua, Sun Chang-yu, et al.. Modified Kalman filter algorithm using equivalent weights with immunity to outliers[J]. Applied Acoustics. 2013, 32(5):409-412.

[9] 吴国清, 李靖, 陈耀明, 等. 舰船噪声识别(Ⅱ)—线谱稳定性和唯一性[J]. 声学学报, 1996, 24(1): 6-11.Wu Guo-qing, Li Jing, Chen Yao-ming, et al.. Ship radiatednoise recognition(Ⅱ)stability and uniqueness of line spectrum[J]. Acta Acustica, 1999, 24(1): 6-11.

[10] Ogle T L and Blair W D. Fixed-Lag Alpha-beta filter for target trajectory smoothing[J]. IEEE Transactions on Aerospace and Electronic System, 2004, 40(4): 1417-1421.

[11] Tucker D G. Detection of pulse signal in noise: trace to trace correlation in visual displays[J]. The Journal of the British Institution of Radio Engineers, 1957, 17(6): 319-329.

[12] 杨晨辉. 被动声呐宽带信号检测与显示方法研究[D]. [硕士论文], 西北工业大学, 2002.Yang Chen-hui. Study on passive sonar broadband detection and display technology[D]. [Master dissertation],Northwestern Polytechnical University, 2002.