一种面向混沌时间序列预测的虚拟特征提取算法

雷 苗 彭 宇彭喜元

(哈尔滨工业大学电气工程及自动化学院 哈尔滨 150080)

1 引言

电力、水利，自动化等实际工程领域里，例如风电功率时间序列[1]，河流径流量[2]，以及间歇式反应釜釜温[3]等时间序列都具有混沌特性。混沌时间序列预测研究包括两个方面：一是改进预测模型；另一个是改进前端的特征提取算法。在模型改进方面，文献[4]采用Jaeger提出的回声状态机制，改进了贝叶斯框架。文献[5]在递归最小二乘支持向量机算法上，引入了局部模糊推理机制。文献[6]采用合作微分进化算法(cooperative coevolution)，改进了Elman递归神经网络。然而模型改进后，一般都训练繁琐，算法复杂度增加。在特征提取改进方面，文献[7]采用误差补偿的方式，把残差视为一种广义的特征。文献[1]采用集成经验模态分解算法和近似熵分析，将风电功率时间序列提取出一系列复杂度差异明显的风电子特征。文献[8]采用ARIMA模型，从混沌时间序列中提取出近似线性特征。然而，文献[9]也指出文献[8]的这类提取算法里，有两个假设前提存在问题：一是线性部分和非线性部分被默认为是加和关系未必合理；二是线性模型未必能将线性部分从原始序列中提取彻底。

本文针对文献[9]指出的线性与非线性特征算法存在的问题，利用平移不变小波算法，把线性部分与非线性部分的加和关系推广到函数关系，并在解析意义下，给出一种新颖的虚拟特征表达。

本文剩余部分结构安排如下：第2节介绍混沌序列预测基础知识；第3节介绍面向混沌时间序列预测的虚拟特征提取算法；第4节介绍仿真和实验；第5节总结全文。

2 面向混沌预测的特征提取相关知识

2.1 面向混沌预测的虚拟特征提取算法框架

下面先给出面向混沌预测的虚拟特征提取算法框架，如图1所示。

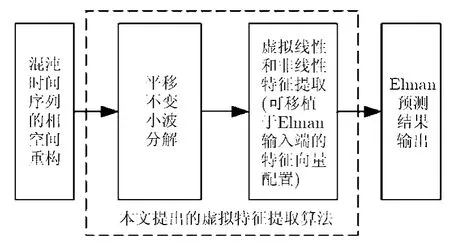
图1 面向混沌预测的虚拟特征提取框架

图1所示的框架分为3个部分。第1部分是混沌相空间重构理论。虚线框中的第2部分是本文提出的虚拟特征提取算法。第3部分，采用Elman预测实验来评估本文特征提取算法的有效性。

2.2 混沌相空间重构与直接多步预测

对于混沌时间序列Y，根据文献[10]的推导可得，存在一个映射满足：

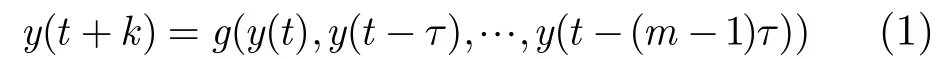
后文实验部分将采用Elman网络直接多步预测的结果，验证本文提出的虚拟特征提取算法。

2.3 Elman递归神经网络

Elman网络是一种典型的递归神经网络，由于较为常见和自身良好的动态特性，已被广泛用于混沌时间序列的预测。具体Elman网络结构、训练过程等详见文献[11]。

3 面向混沌序列预测的虚拟特征提取算法

3.1 算法基本思想

文献[8]假设时间序列Y由线性特征L和非线性特征N两部分以加和关系构成，即

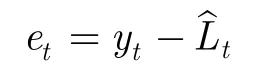
精确的线性特征Lt无法获得，文献[8]等采用ARIMA模型的预测值来近似线性特征，从而et即为ARIMA的剩余部分。文献[8]又采用神经网络模型对et进行预测，理想的映射关系如下：

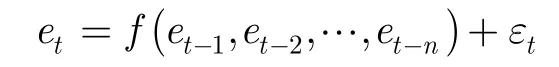
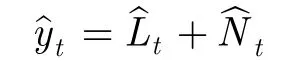
但文献[9]指出，此线性与非线性特征提取算法里，有两个假设前提存在问题：一是线性部分和非线性部分被默认为是加和关系未必合理；二是线性模型未必能将线性部分从原始序列中提取彻底。

针对以上两个问题，本文首先将线性、非线性特征与原时间序列Y的关系推广到函数关系，即

而后，对于线性和非线性特征，本文并不试图在预测过程中给出Lt和Nt显式的数值结果；而只保留它们与预测输出之间的映射关系，仅仅是把Lt和Nt视为用于预测时间序列Y的过渡特征。本文把这样的Lt和Nt定义为虚拟过渡特征，后文简记为虚拟特征(virtual feature)。事实上，虚拟特征本质就是可移植于神经网络非线性输入端的过渡特征向量。

3.2 虚拟特征提取两子部分

3.2.1 平移不变小波变换 小波分析以其良好的时频局部化特性和多分辨分析能力，被广泛应用于各种信号及图像处理研究中。

平移不变小波变换(shift invariant wavelet transform)被成功应用于各类时间序列预测问题[12]。文献[13]验证了不同形式的平移不变小波变换的等价性，文献[14]将它们统一命名为平移不变小波。

文献[15]给出了平移不变小波正、逆变换，以实现序列Y的多分辨分析， 得到Y的重构公式为

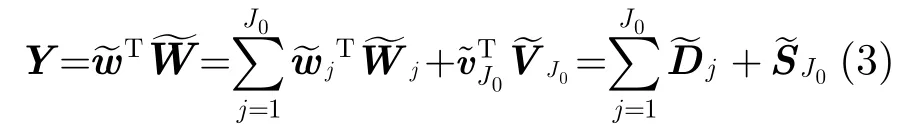
3.2.2 虚拟线性与非线性特征表达 如前所述，由原混沌序列Y经平移不变小波分解后得到若干光滑和细节子层。

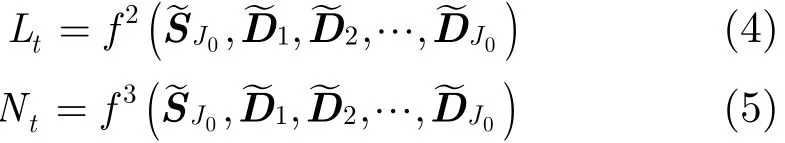
联合式(2)可得

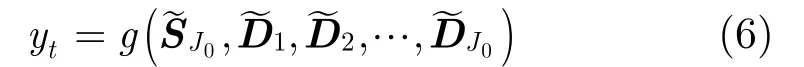
其中，g为非线性映射函数。本文采用Elman神经网络实现，假设Elman神经网络实际的预测值为ˆty，则总的预测结果为

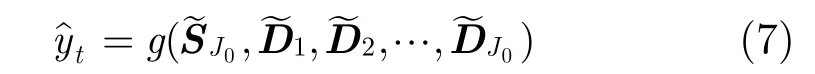
3.3 面向预测的虚拟特征提取算法步骤

下面给出面向预测的虚拟特征提取算法步骤。

步骤 1 确定混沌时间序列Y的嵌入维数m和嵌入延迟τ，进行相空间重构；

步骤 2 采用式(3)进行平移不变小波变换，获取若干个光滑和细节子层；

步骤 3 根据式(7)，采用Elman神经网络，对特征提取后的信息进行直接多步预测。

4 仿真实验和结果分析

本文采用两类典型的混沌数据，仿真和实测混沌数据，验证本文提出的虚拟特征提取算法的有效性。具体为Mackey-Glass系统仿真数据，以及美国密西西比河某监测站实测径流流量数据。

选取均方误差MSE (Mean Square Error)和规范化均方误差 NMSE (Normalized Mean Square Error)作为预测精度评价标准，将本文提出的虚拟特征提取算法用于预测实验，与Elman直接预测等其它4种预测方法进行对比。为预测值，为其对应真值，，其中M为测试数据点对数。定义：

5种预测方法均采用直接多步预测的结果进行比对。实验中，取直接多步预测的步数k =6。

4.1 仿真数据结果

Mackey-Glass预测是研究混沌时间序列预测的标杆问题。Mackey-Glass序列由式(10)微分方程产生：

实验中，取微分方程参数a=0.2, b=0.1, c=10,，同时取定初值，采样间隔，用四阶Runge-Kutta法解微分方程，可得混沌时间序列Y，如图2所示。

Mackey-Glass虚拟特征提取和预测实验中，取嵌入维数m=4，嵌入延迟5τ=。同时从Y中取500点对训练，500点对预测。

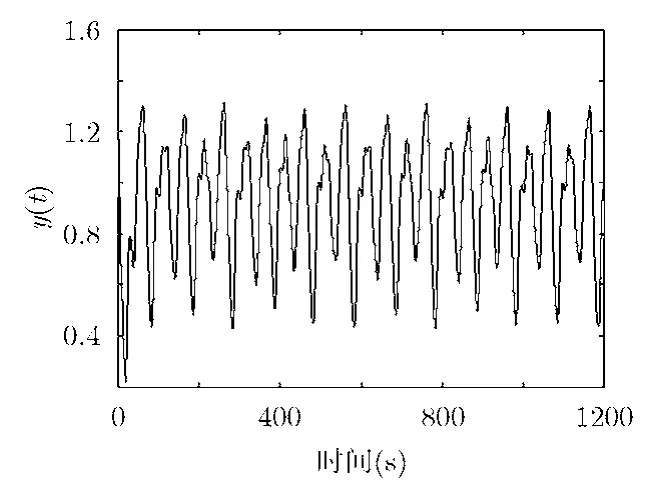
图2 Mackey-Glass混沌时间序列

图3给出Mackey-Glass的各个平移不变小波光滑和细节子层。选取Haar小波基，分解层数为2层。其中Y为原混沌时间序列，D1～D2为第1至第2个细节子层，S2为光滑子层。

图4给出本文算法应用于直接多步预测实验，预测值和真实值的对比图。

表1给出本文算法以及Elman直接预测等5种方法的预测精度指标。由表1可知，本文算法在Mackey-Glass混沌时间序列预测上，相对于其它4种方法中表现最好的Elman直接预测算法，MSE,NMSE分别降低50%和50%。

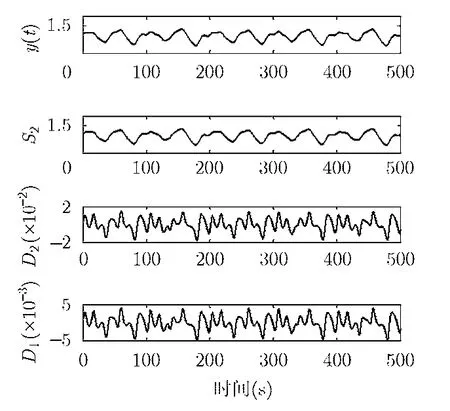
图3 Mackey-Glass序列平移不变小波光滑和细节子层

4.2 实测数据结果

为了进一步验证本文算法的有效性，下面选取2008年1月1日至2012年9月30日，美国密西西比河某监测站实测径流流量数据进行实验验证。文献[2]引证了密西西比河实测流量数据具有混沌特征。本文选取500点对用于训练，500点对用于预测。实验中取嵌入维数m=2, 嵌入延迟1τ=。

Elman直接预测以及本文算法两种不同方法预测的误差结果如图5所示。

由图5可知，虚线加号代表的Elman直接预测误差较大；实线圆圈代表的本文方法误差较小。

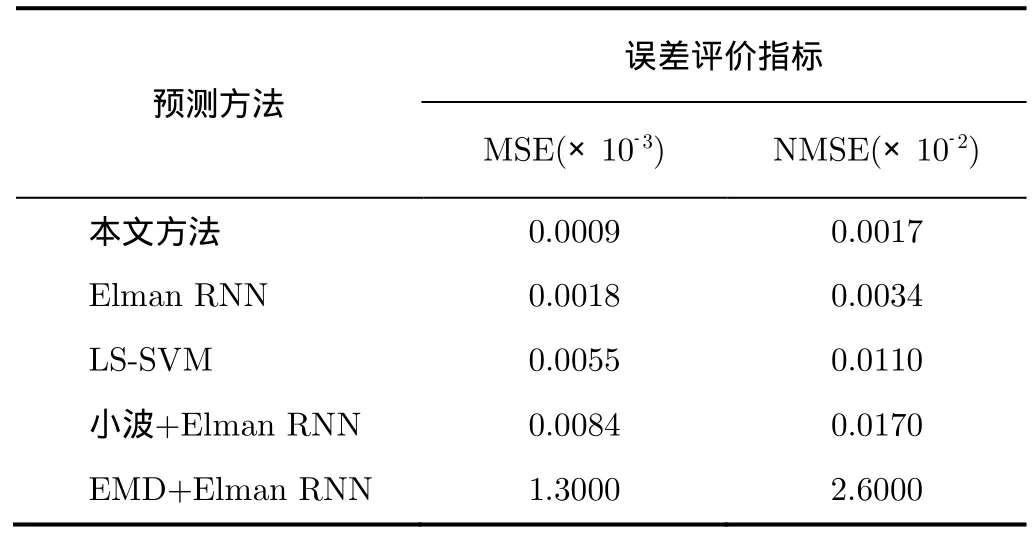
表1 Mackey-Glass预测误差对比

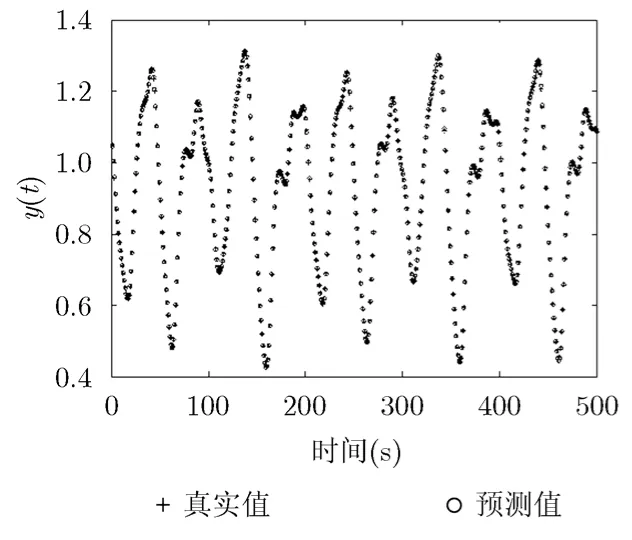
图4 Mackey-Glass虚拟特征提取多步预测结果

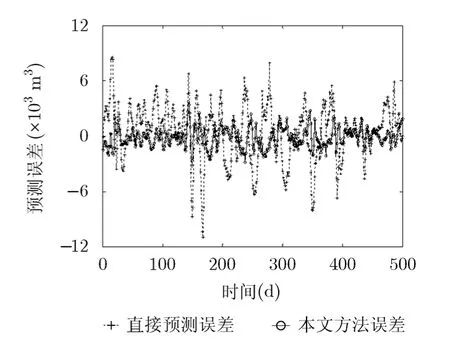
图5 Mississippi混沌时间序列预测误差对比

由表2可知，本文算法在美国密西西比河某监测站实测径流流量数据预测上，相对于其它4种方法中表现最好的小波分解加Elman模型，MSE, NMSE也分别降低36%和35%。从而也验证了本文算法在实测Mississippi混沌数据上的有效性。

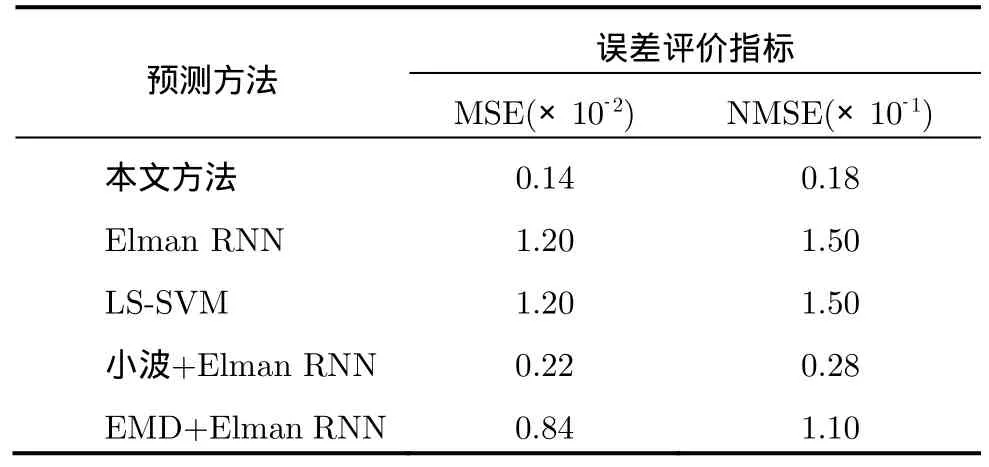
表2 Mississippi预测误差对比

5 结束语

针对混沌时间序列预测需求，本文把线性部分与非线性部分的加和关系推广到函数关系。然后，利用平移不变小波细节和光滑子层信息，给出了一种新颖的虚拟特征表达。

采用经典的Mackey-Glass仿真数据，以及美国密西西比河实测径流流量数据实验表明，本文提出的虚拟特征提取算法较Elman直接预测等其它4种方法，预测误差降低，预测精度提高。

然而，本文方法主要是利用了平移不变小波的多分辨特性和解相关特性，提取出初始子层信息。整个特征提取过程，对混沌时间序列的背景信息和先验知识考虑较少。如何利用电力、水利、自动化等实际工程领域实测混沌时间序列的背景信息反馈回小波基函数的设计，提高特征提取的针对性，是本文需要深入研究的问题。

[1] 张学清, 梁军. 基于EEMD-近似熵和储备池的风电功率混沌时间序列预测模型[J]. 物理学报, 2013, 62(5):050505-1-050505-10.Zhang Xue-qing and Liang Jun. Chaotic time series prediction model of wind power based on ensemble empirical mode decomposition-approximate entropy and reservoir[J].Acta Physica Sinica, 2013, 62(5): 050505-1-050505-10.

[2] Kourafalou V H and Androulidakis Y S. Influence of mississippi river induced circulation on the deepwater horizon oil spill transport[J]. Journal of Geophysical Research: Oceans,2013, 118(8): 3823-3842.

[3] 宋彤, 李菡. 基于小波回声状态网络的混沌时间序列预测[J].物理学报, 2012, 61(8): 90-96.Song Tong and Li Han. Chaotic time series prediction based on wavelet echo state network[J]. Acta Physica Sinica, 2012,61(8): 90-96.

[4] Li D, Han M, and Wang J. Chaotic time series prediction based on a novel robust echo state network[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012,23(5): 787-799.

[5] Miranian A and Abdollahzade M. Developing a local least-squares support vector machines-based neuro-fuzzy model for nonlinear and chaotic time series prediction[J].IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(2): 207-218.

[6] Rohitash C and Zhang M J. Cooperative coevolution of Elman recurrent neural networks for chaotic time series prediction[J]. Neurocomputing, 2012, 86(1): 116-123.

[7] 韩敏, 许美玲. 一种基于误差补偿的多元混沌时间序列混合预测模型[J]. 物理学报, 2013, 62(12): 120510-1-120510-7.Han Min and Xu Mei-ling. A hybrid prediction model of multivariate chaotic time series based on error correction[J].Acta Physica Sinica, 2013, 62(12): 120510-1-120510-7.

[8] Zhang G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50(1):159-175.

[9] Taskaya T and Casey M C. A comparative study of autoregressive neural network hybrids[J]. Neural Networks,2005, 18(5): 781-789.

[10] Han M, Xi J H, Xu S G, et al.. Prediction of chaotic time series based on the recurrent predictor neural network[J].IEEE Transactions on Signal Processing, 2004, 52(12):3409-3416.

[11] Muhammad A F and Saeed Z. Chaotic time series prediction with residual analysis method using hybrid Elman NARX neural networks[J]. Neurocomputing, 2010, 73(13):2540-2553.

[12] Peng Yu and Lei Miao. Multiresolution analysis and forecasting of mobile communication traffic[J]. Chinese Journal of Electronics, 2013, 22(2): 373-376.

[13] 潘泉, 孟晋丽, 张磊, 等. 小波滤波方法及应用[J]. 电子与信息学报, 2007, 29(1): 236-242.Pan Quan, Meng Jin-li, Zhang Lei, et al.. Wavelet filtering method and its application[J]. Journal of Electronics ＆amp;Information Technology, 2007, 29(1): 236-242.

[14] Berkner K and Wells R O. Smoothness estimates for soft-threshold denoising via translation-invariant wavelet transforms[J]. Applied and Computational Harmonic Analysis,2002, 12(1): 1-24.

[15] Mondal D and Percival D B. Wavelet variance analysis for random fields on a regular lattice[J]. IEEE Transactions on Image Processing, 2012, 21(2): 537-549.