稀疏信号重构的阈值化迭代检测估计

宋和平王国利

①(江苏大学计算机科学与通信工程学院 镇江 212013)②(中山大学信息科学与技术学院 广州 510006)

1 引言

近年来，稀疏信号处理成为信号处理和应用数学等领域的一个新研究热点，特别是新兴发展的压缩传感(Compressed sensing, CS)理论[1,2]。压缩传感为稀疏信号处理提供了一个新的方向，可以通过欠采样的线性测量重构稀疏信号。压缩传感开创了很多新的应用，为此，多个国际期刊专门为压缩传感出版了专刊，总结了当前的研究进展[35]-。

压缩传感由欠采样的线性测量重构未知稀疏信号，其稀疏信号重构是求解一个带稀疏约束的欠定线性问题即0ℓ优化问题。然而，0ℓ问题是个NP难的非凸组合问题。为此，压缩传感的奠基工作[1,2]提出用1ℓ问题代替0ℓ问题，即基追踪(Basis Pursuit,BP)问题[6]。此后，很多研究人员提出各种稀疏信号重构的计算方法[7]。一般地可以分为3种：凸松弛算法、贝叶斯推理和贪婪算法。凸松弛算法将稀疏信号重构的0ℓ问题替换为凸优化问题，如BP算法[6]等。贝叶斯推理算法由稀疏先验模型求解最大后验估计，如贝叶斯压缩传感(Bayesian Compressive Sensing, BCS)[8]等。凸松弛算法依赖于最优化算法的实现，相对来说计算比较复杂耗时；贝叶斯推理算法依赖于信号的先验假设，而且算法参数比较多。贪婪算法具有易于设计实现、计算复杂度相对低的特点，吸引了很多研究者的关注。常见的算法有正交匹配追踪(Orthogonal Matching Pursuit,OMP)[9]、子空间追踪(Subspace Pursuit, SP)[10]、压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)[11]、分阶段正交匹配追踪(Stagewise Orthogonal Matching Pursuit,StOMP)[12]和迭代硬阈值化算法(Iterative Hard Thresholding, IHT)[13]等。迭代硬阈值化是一种简单实用的稀疏信号重构方法，但其收敛速度比较慢。最近，文献[14]提出一种新的加速算法双超松弛阈值化算法(Double OverRElaxation thresholding,DORE)。DORE算法是一种基于条件期望值最大化(Expectation Conditional Maximization Either,ECME)迭代的加速算法，其中 ECME由方差未知的高斯模型推导。对稀疏度k未知情况，文献[14]提出一种自动双超松弛阈值化算法(Automatic Double OverRElaxation thresholding, ADORE)。借用文献[15]的概念，本文把这一类算法分为单阶段阈值化(One-Stage Thresholding, OST)和双阶段阈值化(Two-Stage Thresholding, TST)①阈值化(Thresholding)是一种非线性函数，如 MATLAB 函数wthresh，定义硬阈值化；软阈值化。本文所述的双阶段阈值化是文献[15]中TST概念的推广。。

鉴于单次求解 BP问题的稀疏重构结果不够理想，特别是对测量次数相对较少的情况，文献[16]提出一种迭代改进 BP的算法迭代支持集检测(Iterative Support Detection, ISD)，其思想是通过迭代支持集检测来改善 BP算法的重构结果。ISD是一个算法框架，具体实现依赖于支持集检测方法。本文借鉴ISD算法中支持集检测的思想，把ISD算法应用于贪婪算法，提出一种新的稀疏信号重构算法框架阈值化迭代检测估计(Iterative Detection Estimation with Thresholding, IDET)。IDET算法框架为设计新的贪婪算法提供了思路，设计新的贪婪算法包括两个方面：(1)选择 OST算法的迭代步作为支持集检测的参考；(2)根据稀疏信号的特征设计支持集检测方法。同时，本文提出该算法框架的实现算法。该实现算法首先检测IHT算法的迭代步得到一个支持集，然后通过求解支持集上的最小二乘问题来估计待重构的稀疏信号，迭代上述两个步骤直至满足停止条件。IDET算法的关键在于支持集检测，本文提出3种适用于快速衰减信号[16]的支持集检测方法。快速衰减信号是指信号的绝对值从大到小衰减很快，常见的有稀疏高斯信号、稀疏拉普拉斯信号和一些幂律衰减信号。

2 基于阈值化的稀疏重构算法

本文关注的是迭代贪婪算法，借用文献[15]的概念，把这一类算法分为单阶段阈值化OST和双阶段阈值化 TST算法。OST算法是本文对应文献[15]中TST提出的概念，是指对算法迭代步进行一次阈值化就能重构稀疏信号的算法。下面将分别介绍OST算法和TST算法。另外，本节将介绍相关的迭代支持集检测ISD算法。

2.1 单阶段阈值化

文献[14]由高斯概率框架推导出ECME迭代：

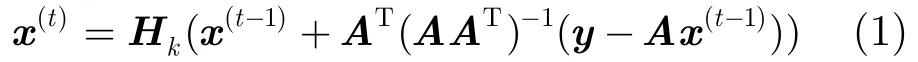
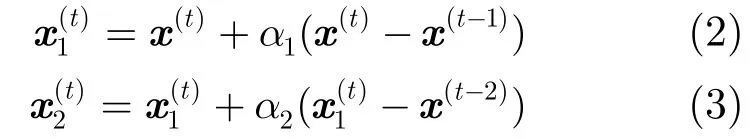
2.2 双阶段阈值化

考虑压缩传感的稀疏信号重构问题，双阶段阈值化TST算法的目的是检测一个支持集I来近似测量向量。待重构的稀疏信号初始赋值为,TST算法迭代计算下面两个步骤：

(1)支持集检测：检测信号x的支持集I，即选择测量矩阵A的哪些列去生成测量向量y，或者说确定用信号x的哪些分量来稀疏表示x。

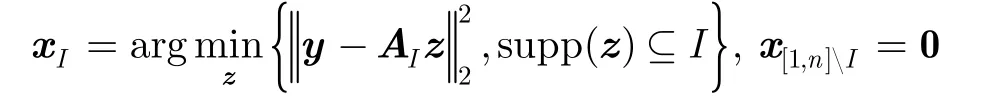
(2)信号估计：通过求解支持集I上的最小二乘问题来更新待重构的稀疏信号x，其中支持集定义为表示集合I在上的补集。TST算法的支持集检测和信号估计分别被认为是一次阈值化，不同算法在支持集检测上各不相同，如OMP, SP, CoSaMP,StOMP等算法分别采用不同的策略进行支持集检测；信号估计都采用支持集上的最小二乘法。

2.3 迭代支持集检测

迭代支持集检测 ISD算法[16]的提出是基于 BP算法的稀疏重构结果，其思想是通过迭代支持集检测来改善 BP算法的重构性能。初始一个支持集, ISD算法迭代计算下面两个步骤：

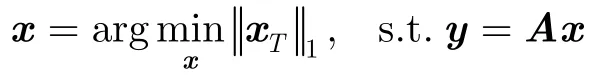
(2)支持集检测： 以第(1)步重构结果x作为参考检测得到一个支持集I。

迭代支持集检测(ISD)是一个算法框架，具体实现依赖于支持集检测方法。文献[16]针对快速衰减信号提出几种有效的支持集检测方法。这里只介绍其中一种简单实用的阈值化方法(如不作特别说明，下文中ISD算法特指由式(4)定义的方法)。

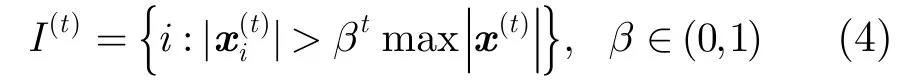
3 阈值化迭代检测估计

鉴于ISD算法在理论和应用上的成功，本文把ISD算法中支持集检测的思想应用到双阶段阈值化TST算法，提出一种新的稀疏信号重构算法框架阈值化迭代检测估计(IDET)，其算法流程如图1所示。阈值化迭代检测估计IDET属于TST算法，它利用 OST算法作为其中支持集检测的参考。IDET算法设计的关键在于：(1)选择合适的OST算法迭代步作为支持集检测的参考；(2)根据稀疏信号的特征设计支持集检测方法。由于ECME的迭代步需要计算存储逆矩阵，特别不适用于大规模应用，本文采用较为简单的IHT迭代步作为支持集检测的参考，设计IDET的实现算法。该实现算法首先检测IHT算法的迭代步得到一个支持集I，然后通过求解支持集I上的最小二乘问题来估计待重构的稀疏信号，迭代上述两个步骤直至满足停止条件。

IDET算法的关键在于支持集检测，根据文献[16]对稀疏信号特征的观察，本文相应的只设计适用于快速衰减信号的支持集检测方法，提出3种不同的方法。综上，提出的IDET实现算法描述为：

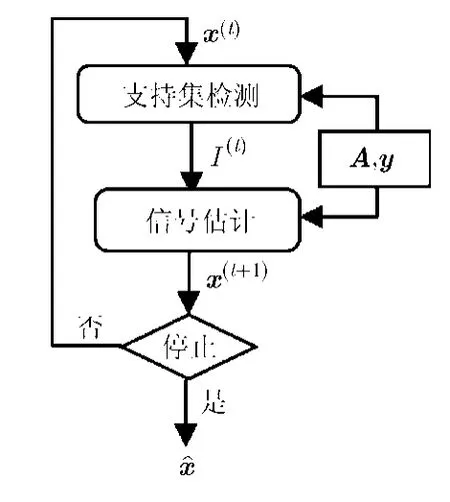
图1 阈值化迭代检测估计(IDET)的算法流程图

(2)支持集检测：更新信号估计：

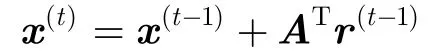
检测支持集I：

(3)信号估计：估计信号：

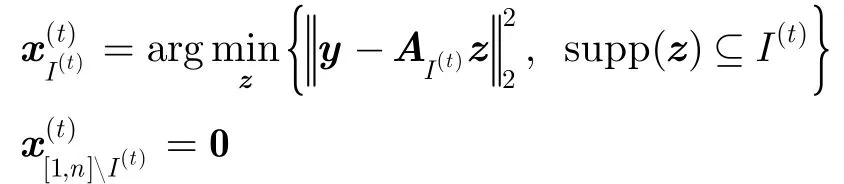
更新残差信号：。

本文提出了3种支持集检测方法，相应的IDET实现算法命名为IDET-k, IDET-β和IDET-γ，其中是阈值化参数。

评注：

(1)IDET算法是本文借鉴ISD算法思想提出的算法框架，其实现算法采用OST算法IHT的迭代步作为参考来检测支持集I。文献[20]是本文算法框架的特例，该算法由基于 Bernoulli-Gaussian模型的二值假设检验推导的迭代步也是IHT的迭代步，但其不涉及支持集检测方法的设计。OMP, SP,CoSaMP等方法采用残差信号与测量矩阵的相关度作为检测支持集的参考，而是最小二乘的负梯度。IDET实现算法中支持集检测参考的是最小二乘的梯度下降迭代步，梯度下降迭代步由于提供了稀疏信号估计在算法设计上更为灵活，可以根据稀疏信号的不同特点设计不同的支持集检测方法。

关于Beats1的运行模式研究，不仅需要分析其优势，还应分析其不足，以便形成更客观和更全面的认识，探索具有良好前景的发展途径。 例如： 目前电台产业的主要用户群体是中老年人，而使用苹果公司产品的主要是青年群体，如何进一步吸引青年群体对音乐的电台模式的兴趣已成为亟待解决的问题； 另外，网络科技的高速发展带来了音乐产品频繁的更新换代，Beats1如何适应产品的快速变化也是不容忽视的方面。 这些都是笔者下一步研究中需要深入探索的课题。

(2)IDET-β算法的支持集检测方法与ISD算法类似，都是通过与指数递减的阈值相比保留绝对值较大的分量。IDET-γ算法的支持集检测方法则保留当前检测到的支持集I，下次迭代在支持集I的补集上作检测。这两种支持集检测方法都不像IDET-k一样每次迭代确定支持集的势为k，适用于稀疏度k未知的应用。

(3)IDET算法思想与ISD算法类似，关键的区别在于支持集检测方法。它们最大的不同之处在于支持集检测参考的是不同的稀疏重构方法。IDET算法支持集检测参考的是OST，而ISD算法支持集检测参考的是BP。由此可见IDET算法比ISD算法在计算复杂度上更具优势。IDET估计信号采用的是支持集I上的最小二乘法，而ISD估计信号是在支持集I的补集上求解BP。由此可见IDET算法比ISD算法更适合于大规模应用。

(4)IDET算法可认为是一种与 DORE不同的OST加速算法。DORE先通过IHT估计稀疏信号，然后通过两步超松弛加速算法，最后进行一次硬阈值化来保证重构的稀疏信号是k稀疏的。DORE需要知道先验稀疏度k，而 IDET-β,IDET-γ不需要这个强条件，只需给定一个阈值化参数即可。采用自动双超松弛阈值化ADORE需要很多次的DORE来估计稀疏度k。

(5)阈值化迭代检测估计的IDET-β和IDET-γ跟阈值化参数有关。阈值化参数越大稀疏重构效果越好，相应地其支持集I增加地越慢，这样需要更多的迭代次数(见实验部分)。

(6)与其他贪婪算法，如OMP, SP, CoSaMP等不同，阈值化迭代检测估计的 IDET-k每次迭代确定支持集的势为k，而不是逐次增加 1或多个(k,2k)索引到支持集I后再进行一次硬阈值化。IDET-β的支持集I是非递增或嵌套的，而 IDET-γ的支持集I是递增或嵌套的。

(7)正如ISD算法所讨论，阈值化迭代检测估计的IDET-β和IDET-γ只适用于快速衰减信号，对那些信号绝对值衰减很慢甚至不衰减(如二值 0/+1、三值0/-1/+1信号)情况不适用，阈值化迭代检测估计的 IDET-k没有这个限制。总体来说，阈值化迭代检测估计IDET算法对非快速衰减信号没有显示出比1ℓ最优化更好的稀疏重构性能[15,21]，但可以通过线性或非线性映射把非快速衰减信号转化为适用于IDET算法的快速衰减信号[22]。

4 计算复杂度分析

阈值化迭代检测估计的 IDET-k, IDET-β和IDET-γ算法主要的计算步骤为矩阵向量乘法(matrix-vector multiplication)。迭代硬阈值化IHT迭代的计算复杂度为 O ( m n)，那么算法 IDET-k,IDET-β和 IDET-γ的更新稀疏信号的计算复杂度为。阈值化步骤的计算复杂度为 O ( n l gk)②)算法IDET-k的支持集检测需找出前k个最大值即计算复杂度为O(nlgk) , IDET-β和IDET-γ的支持集检测只需两次遍历查找即计算复杂度为O(2n)，求解支持集上的最小二乘所采用的近似共轭梯度法的计算复杂度为为近似共轭梯度法迭代次数)③算法IDET-β和IDET-γ支持集I变化不一，但|I|≤k，这里以|I|≤k计算。实验部分近似共轭梯度法迭代次数设为20。，更新残差信号的计算复杂度为，那么每次迭代所需计算复杂度总和为。双超松弛阈值化法(DORE)算法两次硬阈值化的计算复杂度为，两次超松弛步骤的计算复杂度为，那么每次迭代所需计算复杂度总和为。IDET算法和DORE算法需存储测量矩阵A，其所需的存储量为。OMP, SP等TST算法的计算复杂度分析参考文献[23]。

5 实验结果

本节介绍仿真实验，所有代码均由 MATLAB实现④所有代码可在https://github.com/songhp/IDET/下载。，部分采用了文献[14,21]提供的代码，运行环境为MATLAB v7.6，计算机操作系统为Windows XP, 2.53 GHz Intel Celeron CPU, 2 GB内存。实验比较算法选择 OST的加速算法 DORE算法和TST算法中性能较好的SP算法[15,21]，IDET算法不与1ℓ最优化(如ISD算法)和其他OST/TST算法(如OMP算法等)比较，这些算法已经在文献[14,15,21]中有详细的比较。算法评价有两组：相变(phase transitions)曲线和 Shepp-Logan Phantom 图像重构，更多的实验比较见文献[23]。

5.1 相变曲线

在实验中，所有测量矩阵A都采用均匀球面矩阵集(Uniform spherical ensemble)，即测量矩阵A是随机高斯矩阵并对A归一化。实验所用k稀疏的信号x是随机选择势为k的支持集，相应的元素值由高斯分布均匀生成。为公平比较算法，实验中迭代停止条件设最大迭代次数为100或相对误差为：。定义为稀疏性度量(sparsity),为不确定性度量(indeterminacy)，那么得到评价稀疏信号重构的 2维相平面。对每一个δ，通过插值找到稀疏重构概率大于0.50的所有ρ，这样得到相变曲线。曲线之下表示稀疏重构成功，反之则失败。越高的相变曲线表示算法重构能力越好。本实验采用文献[21]所用代码生成相变曲线。确定稀疏信号维数，线性选取16 对。每对实验运行 100 次。采用是真实稀疏信号)判定稀疏重构准确。

实验测试阈值化参数β对算法 IDET-β的影响，设β=0.7,0.8,0.9，选取δ=0.05, 0.20, 0.35, 0.50，阈值化参数β对算法IDET-β的影响如图2所示，相应的相变曲线如图3所示。从图中可以看出，β越大稀疏信号重构的准确重构率越高，稀疏重构性能越好。同样地，测试阈值化参数γ对算法IDET-γ的影响，设γ=0.7,0.8,0.9，选取δ=0.05, 0.20, 0.35,0.50，阈值化参数γ对算法 IDET-γ的影响如图 4所示，相应的相变曲线如图3所示。从图中可以看出，γ越大稀疏信号重构的准确重构率越高，稀疏重构性能越好。图5实验对比了DORE, SP算法与IDET-k算法的准确重构率，可以看出 IDET-k比DORE准确重构率高，稀疏重构性能更好；在m/n比较大时，SP比IDET-k稀疏重构性能更好。从图3可以看出，所有算法中DORE算法稀疏重构性能最差，阈值化迭代检测估计的IDET-β, IDET-γ依赖于阈值化参数，参数越大算法稀疏重构性能越好；SP算法在m/n＞0.4时显示出更好的稀疏重构性能。

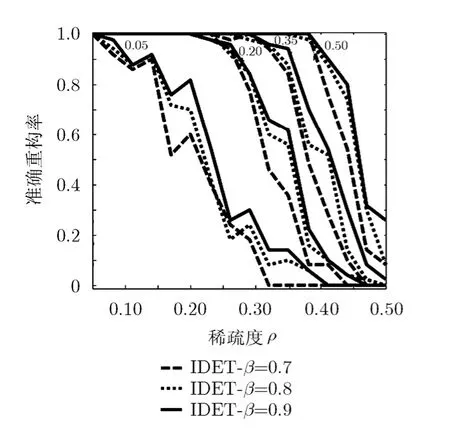
图2 算法IDET-β不同阈值化参数的准确重构率比较

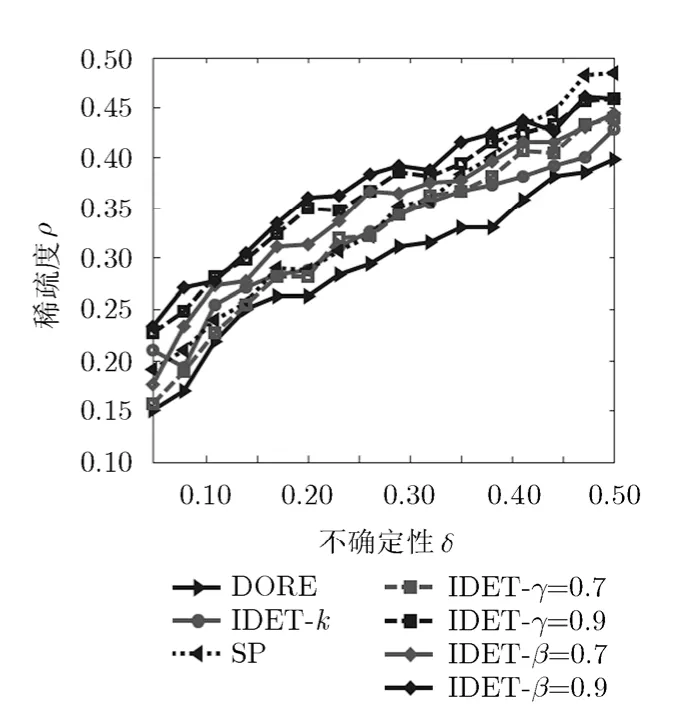
图3 算法DORE, SP,IDET的相变曲线比较

图4 算法IDET-γ不同阈值化参数的准确重构率比较

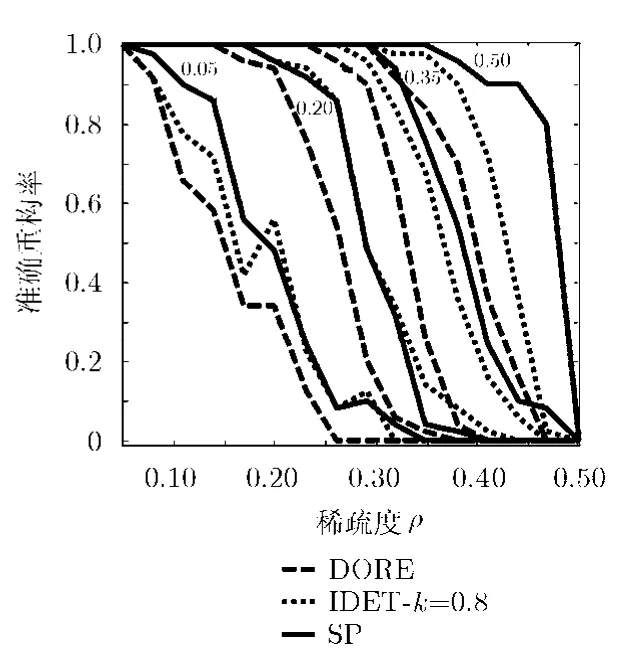
图5 算法DORE, SP与IDET -k的准确重构率比较

5.2 图像重构

本小节实验比较IDET算法与DORE, SP算法重构Shepp-Logan Phantom图像。测量向量y是2维离散傅里叶变换射线采样系数。测量矩阵是采样矩阵(部分离散傅里叶变换矩阵)，是稀疏化矩阵(逆 Harr小波变换)。Shepp-Logan Phantom图像的Harr小波变换系数是稀疏的。稀疏重构性能评价标准采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)、迭代次数和 CPU运行时间。峰值信噪比，其中0x是Harr小波变换系数，分别表示Shepp-Logan Phantom图像的最大值、最小值。为公平比较算法，实验中迭代停止条件设最大迭代次数为1000或相对误差为：。对图像大小为256×256，设e =0.01, β=0.8, γ=0.8。图 6显示的是图像射线采样数为35～50时IDET算法与DORE, SP算法的重构结果比较。IDET的3个实现算法IDET-k, IDET-β, IDET-γ重构图像的 PSNR都要比 DORE, SP算法大。算法 SP,IDET-β迭代次数要比其他算法少，IDET-k在射线采样数比较高时，其迭代次数下降很明显。算法IDET-γ和DORE在很多情况下维持比较高的迭代次数，但就 CPU 运行时间而言，IDET-γ跟 SP,IDET-β, IDET-k一样要比DORE算法少很多。

图6 重构Shepp-Logan Phantom图像的峰值信噪比PSNR、迭代次数和CPU运行时间比较

6 结束语

本文研究压缩传感的稀疏信号重构算法，把贪婪算法分为两类：OST与TST。受ISD算法思想的启发，本文提出一种结合OST和TST的贪婪算法框架IDET。IDET算法与传统的TST不同之处在于采用OST作为支持集检测的参考，可以根据稀疏信号的特征设计相应的支持集检测方法。针对快速衰减信号，IDET的实现算法设计了 3种检测IHT迭代步的方法。实验结果表明，IDET实现算法比 DORE算法、SP算法(大多数情况下)具有更好的稀疏重构性能。贪婪算法以其快速、易于实现(特别是对大规模应用)的特点在压缩传感研究领域得到广泛的关注，如国内的研究[24]。IHT之类的OST算法实现简单，但其收敛比较慢。本文提出的IDET实现算法是一种比DORE算法更具优势的IHT加速算法。根据IDET算法思想，我们可以设计更多的OST加速算法。ISD算法在理论与实践上表明重构相同稀疏度的稀疏信号所需的测量次数比 BP算法更少，为此，研究IDET算法在理论上减少测量次数成为新的方向。

[1] Candes E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[3] Bajwa W, Leus G, Scaglione A, et al.. Guest editorial: special issue on compressive sensing in communications[J]. Physical Communication, 2012, 5(2): 61-63.

[4] Allstot D, Rovatti R, and Setti G. Editorial: special issue of compressive sensing[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012, 2(3): 337-339.[5] Ahmad F, Arce G, Narayanan R, et al.. Special section guest editorial: compressive sensing for imaging[J]. Journal of Electronic Imaging, 2013, 22(2): 020901-1-020901-2.

[6] Chen S, Donoho D, and Saunders M. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159.

[7] Qaisar S, Bilal R, Iqbal W, et al.. Compressive sensing: from theory to applications, a survey[J]. Journal of Communications and Networks, 2013, 15(5): 443-456.

[8] Ji S, Xue Y, and Carin L. Bayesian compressive sensing[J].IEEE Transactions on Signal Processing, 2008, 56(6):2346-2356.

[9] Tropp T and Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655-4666.

[10] Dai W and Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249.

[11] Needell D and Tropp J. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Communications of the ACM, 2010, 53(12): 93-100.

[12] Donoho D, Tsaig Y, Drori I, et al.. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121.

[13] Blumensath B and Davies M. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3): 265-274.

[14] Qiu K and Dogandzic A. Sparse signal reconstruction via ECME hard thresholding[J]. IEEE Transactions Signal Processing, 2012, 60(9): 4551-4569.

[15] Maleki A and Donoho D. Optimally tuned iterative reconstruction algorithms for compressed sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):330-341.

[16] Wang Y and Yin W. Sparse signal reconstruction via iterative support detection[J]. SIAM Journal on Imaging Sciences,2010, 3(3): 462-491.

[17] Yin W, Osher S, Goldfarb D, et al.. Bregman iterative algorithms for l1-minimization with applications to compressed sensing[J]. SIAM Journal on Imaging Sciences,2008, 1(1): 143-168.

[18] Beck A and Teboulle M. A fast iterative shrinkage thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202.

[19] Blumensath T. Accelerated iterative hard thresholding[J].Signal Processing, 2012, 92(3): 752-756.

[20] Amini A, Babaie-Zadeh M, and Jutten C. A fast method for sparse component analysis based on iterative detectionestimation[C]. International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering,Paris, France, 2006: 123-130.

[21] Sturm B. Sparse vector distributions and recovery from compressed sensing[OL]. http://arxiv.org/pdf/1103.6246v2,2013.10.

[22] Zhang X, Wen J, Han Y, et al.. An improved compressive sensing reconstruction algorithm using linear non-linear mapping[C]. Proceedings of Information Theory and Applications Workshop, La Jolla, CA, USA, 2011: 1-7.

[23] 宋和平. 稀疏信号重构的贪婪算法及其应用[D]. [博士论文],中山大学, 2011.Song He-ping. Greedy algorithms with application to sparse signal recovery[D]. [Ph.D.dissertation], Sun Yat-Sen University, 2011.

[24] 刘记红, 黎湘, 徐少坤, 等. 基于改进正交匹配追踪算法的压缩感知雷达成像方法[J]. 电子与信息学报, 2012, 34(6):1344-1350.Liu Ji-hong, Li Xiang, Xu Shao-kun, et al.. Compressed sensing radar imaging methods based on modified orthogonal matching pursuit algorithms[J]. Journal of Electronics ＆amp;Information Technology, 2012, 34(6): 1344-1350.