基于三角多项式插值的频率和相位联合估计算法

胡景明 叶 展 张邦宁

（解放军理工大学通信工程学院，南京，210007）

引 言

完成载波（包括频率和相位）同步是相干数字接收机实现的前提，其性能好坏直接影响到接收机的误码率指标。近年来，随着Turbo码、低密度校验码（Low density parity check code，LDPC）等先进编码技术的应用，低信噪比接收技术成为现代通信发展的重要方向，但过低的信噪比给接收机载波同步带来了新的挑战，如何成功完成低信噪比条件下的载波同步，并保证足够的精度，已成为急需解决的重要课题。

载波同步过程中频率和相位估计是关键，常见的估计算法可分为时域类和频域类两大类。时域类算法中，Fitz算法［1］具有很高的估计精度，但存在适应的频率动态范围有限、运算量大、硬件实现代价高等缺点；文献［2－3］针对Fitz算法进行了改进，提升了算法适应的频率范围，但性能损失较大，同时未能克服其运算量大的缺点。频域类算法具有适应频率动态范围大的优势，由于可采用FFT降低运算量，还具有实现复杂度低、硬件开销小的优点，但由于“栅栏效应”，直接FFT运算很难获得精确的频率估计。为了提高估计精度，须在已有FFT谱线的基础上，通过插值来提高估计精度，其中典型的有 Rife算法［4－5］和 Quinn算法［6］，但 Rife算法和Quinn算法在某些频率点上的估计精度恶化严重，难以满足低信噪比通信的要求；文献［7］提出了利用三根谱线进行插值的三线幅度法，其精度较Rife和Quinn算法有了显著的改进，缺点是FFT运算长度增加了一倍，导致运算量显著增加；文献［8－11］提出了迭代的载波估计算法，估计精度逼近CRB界，但代价是增加了运算量和时延，不利于突发信号的实时接收；文献［12－15］提出了基于正弦波和实时高精度的频率估计算法，但这些算法不能满足信噪比较低的要求，而且运算复杂度也较高。

本文研究频域类载波估计算法，采用基于三角多项式插值的频率和相位联合估计，给出了对应的实现方案。与Rife，Quinn相比，本文算法的实现复杂度与其基本相当，但估计精度得到显著提高；与三线幅度法相比，本文算法运算量仅约为其一半，且性能略优；与迭代类载波估计算法相比，本文算法精度与其基本相当，但省去了迭代过程，运算量和处理延迟显著减小。

1 频率和相位估计基本模型

假设接收信号经准确位定时同步，用数据辅助法去除调制信息后可表示为

求解可得

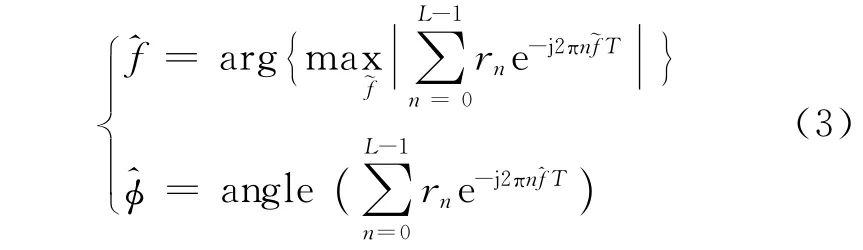
其中angle（·）表示在－π～π范围内求复数的辐角。式（3）的求解非常困难，只能用搜索最大值的办法来解决，考虑到运算量因素，该搜索过程一般用FFT运算来实现。办法是对接收序列rn做FFT运算，搜寻幅度最大的FFT谱线，其对应的频率和相位即为所求的值。但由于FFT的“栅栏效应”，其估计精度会受到严重限制，难以满足接收机对精度的要求。

从图1可以看到，有限长度的单频信号频谱呈“sinc”函数包络，直接对观察信号FFT运算后可以获得“sinc”包络主瓣内的两根谱线，这样其最大频率估计误差可达FFT谱线间隔的一半，即Rs／（2L），其中Rs表示符号速率。通过补零可在一定程度上提高搜索的精度（如图2所示），但其代价是大大增加了运算量，不适合于精度要求很高的场合。

图1 信号直接FFT运算后谱线示意图Fig.1 Signal′s spectrum after FFT

图2 信号经1倍补零FFT运算后谱线示意图Fig.2 Signal′s spectrum after FFT when appended with one time zeros

要获得精确的频率估计，须在FFT基础上再运用插值运算来提高估计精度，即通过插值估计出频率值应精确地位于FFT谱线间的何处（即图1和图2中所示的μ值）。

根据频率内插公式，FFT后频谱间任意点的值R＋μ）值都可通过FFT序列｛R（l）｝得到

这样精确的频率估计就转化为求解式（4）取最大幅度时所对应的μ值，即

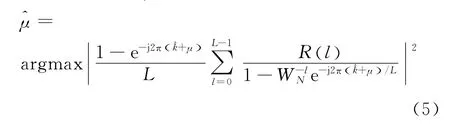
遗憾的是，该式求解同样非常困难。为了便于求解，实际运算中往往寻求各种简化的替代办法，其中最经典的属Rife算法和Quinn算法。Rife算法利用FFT谱线呈“sinc”包络的特性，根据“sinc”主瓣内两根谱线的幅度，经过插值提高估计精度；Quinn算法与Rife算法类似，不同之处在于它是利用谱线之比的实部。相对而言，Quinn算法的估计精度和稳定性均优于Rife算法，但与Rife算法一样，均存在严重的稳定性问题；三线幅度法可看做是Rife算法的改进，通过“sinc”包络内的3根谱线幅度的插值获得精确的频率和相位估计。

2 基于三角多项式插值的频率和相位联合估计算法

2.1 基本算法和求解过程

与Rife、Quinn及三线幅度法不同，本文采用新的插值方法——三角多项式插值，通过简化和求解，获得精确的频率和相位估计结果。三角多项式插值算法由文献［16］在2005年提出，其目的是用于实现位定时同步，但经过分析和仿真，发现将其用于此处的频率和相位估计，同样能获得精确的结果。

三角多项式插值算法至少需要4个样点，假定已经通过运算获得了“sinc”函数包络内的4根谱线，分别记为R（l－1），R（l），R（l＋1）和R（l＋2），如图2所示。然后要估计出实际频率位于l与l＋1间的何处，即μ值，根据文献［16］，｜R（l＋μ）｜2（0≤μ＜1）值可用四点三角多项式插值运算来近似，即

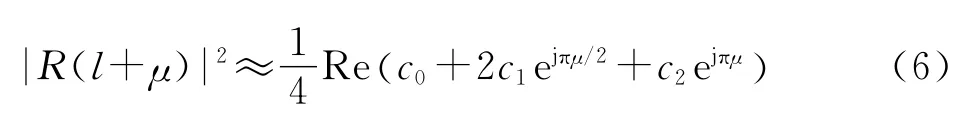
式中：c0＝｜R（l－1）｜2＋｜R（l）｜2＋｜R（l＋1）｜2＋｜R（l＋2）｜2，c1＝［｜R（l）｜2－｜R（l＋2）｜2］＋j［｜R（l－1）｜2－｜R（l＋1）｜2］，c2＝｜R（l）｜2－｜R（l＋1）｜2＋｜R（l＋2）｜2－｜R（l－1）｜2。

这样，精确的频率和相位的估计转化为μ值的估计为

式（7）仍不易求解，还需进一步简化。由“sinc”函数的对称性可知c2≈0，可将其忽略，同时由于c0是个正实数，因此式（7）求解为

这样可得频率的估计值为

获得频率估计后，根据FFT谱线与相位的对应关系式，可得到相位的估计值为

式（10）中的R（k）应选择最大幅度的FFT谱线，其取值为R（l）和R（l＋1）中的较大者。在实际估计的过程中，更关心观测序列中点所在的相位。将初始相位值转换为观测区间中点的相位，频率和相位估计可统一表示如下

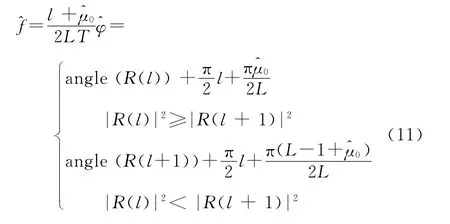
2.2 估计偏差的修正

图3是算法在无噪声时的频率估计曲线，可以看出该估计是有偏估计，即L＝128时最大的估计偏差在2×10－5以内，该精度能够满足大部分接收机的要求，但对于精度要求极高的场合尚显不足。

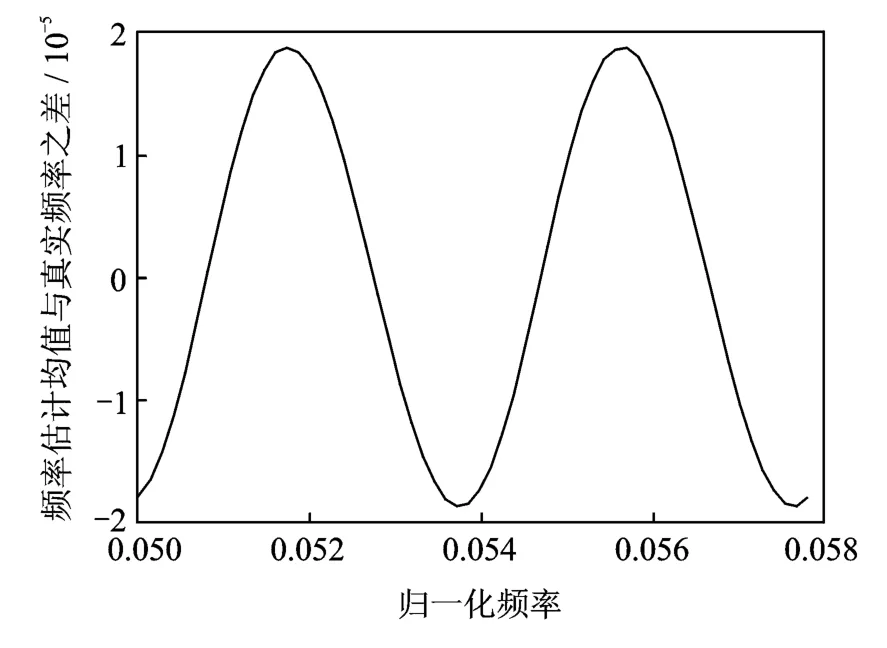
图3 L＝128无噪声时的频率估计仿真曲线Fig.3 Simulation curve of frequency estimation at L＝128with no noise

从2.1节分析可知，算法在最大似然估计基础上使用了四点三角插值公式，忽略了c2项，这些近似处理必然带来误差，直接后果是导致频率估计不能满足无偏估计的要求，图3的频率估计偏差即来源于此，具体的说来源于μ值的估计误差，即

根据式（12）可方便地绘制出无噪声时Δμ与μ值的关系曲线，如图4所示。可根据该曲线对估计偏差进行修正，提高估计精度。具体实现时可采用查找表的办法，即将无噪声条件下Δμ与μ0的曲线制作成查找表，实际进行频率和相位估计时用值去查表得到Δμ值，并用其对估计结果进行修正

相应地，式（11）的频率和相位估计值修改为

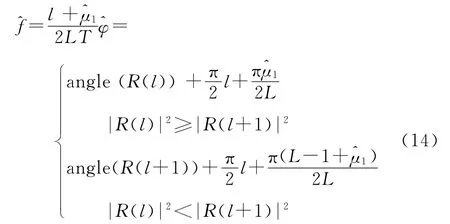
图5是修正后的频率估计误差曲线，可看出估计偏差低于5×10－9，精度极高。

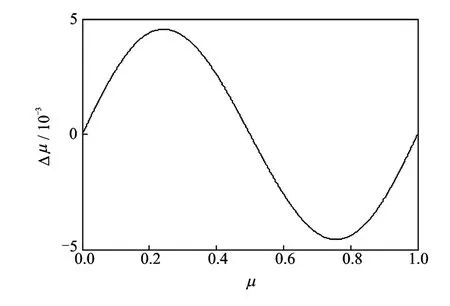
图4 式μ值的估计误差曲线Fig.4 Estimating error curve ofμ－value from Eq.（12）

图5 L＝128无噪声时修正后的频率估计仿真曲线Fig.5 Simulation curve of modified frequency estimation at L＝128with no noise

3 算法的实现方案

对于频域类载波估计算法，其主要运算量体现在FFT运算。若采用普通的基2FFT运算，Rife和Quinn算法需要做长为L的FFT运算，所需的复乘次数约为Llog2L／2。本文采用的基于三角多项式插值的频率和相位估计，需要获得“sinc”主瓣内的四根谱线，但直接对L点的观察信号做FFT运算仅可获得“sinc”主瓣内的两根谱线。故有以下两种方案。

3.1 基于补零的FFT运算（方案1）

文献［17］的三线幅度法通过对观测数据末尾补零，并做2L点的FFT运算，可将频谱分辨率提升一倍，获得“sinc”主瓣内的2根谱线。文献［10］也采用了完全类似的实现方法，本文同样可借鉴。

该实现方案的主要问题是FFT运算长度增加1倍，由于有一半为零值，实际实现时可分解为两次L长度的FFT运算。这样与Rife和Quinn算法相比，方案一的运算量近似翻番。

3.2 基于加窗的频率插值法（方案2）

另一种可行的办法是直接计算出“sinc”主瓣内的另外两根谱线R（k±1／2），可采用的计算方法有两种，一种是直接根据时域信号计算，另一种是根据FFT运算后的结果通过频率内插公式计算。

直接根据时域信号计算的思路非常简单，即直接根据傅里叶变换的定义计算频谱，其计算式为

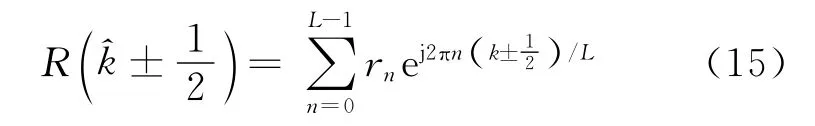
该方法需重新计算L项的复乘并相加，文献［9－11］推荐采用该计算方法，但式（15）当L较大时该运算量非常可观。

还有一种计算方法是根据FFT的结果，利用式的频率内插公式进行计算。该方法同样包括L项复数的运算，但由于信号的频谱呈“sinc”状，FFT谱线的主要能量都集中在“sinc”主瓣附近，其余处谱线接近于0，所以运算要简单的多，即利用式的频率内插公式计算R±1／2）时仅需计算k附近的若干项即可。定义窗长度参数为I，有

显然，窗口参数I取值越大则式（16）的计算越精确，用三角多项式插值估计的频率和相位精度也越高。后面的仿真表明，当I≥6估计精度已经非常接近方案1了，但其运算量要小很多。

通过计算获得主瓣内的另两根谱线R（k±1／2）后，接下来要做的是选取出“sinc”主瓣内的4根谱线做插值，如图6所示。有两种情况：当｜R（k－1／2）｜＞｜R（＋1／2）｜时，选择R－1／2），R），R（＋1／2）和R（k＋1）；反之则应选择R－1），R－1／2），R）和R＋1／2），它们分别与算法描述中的R（l－1），R（l），R（l＋1）和R（l＋2）相对应。

这样，本文算法的实现方案总结如下：

步骤1：对所观察序列做FFT运算，并找出幅度最大的谱线位置，标记为

步骤2：分别根据方案1或方案2，计算出R（±1／2），并选择出“sinc”包络主瓣内的4根谱线。

步骤3：通过式（17）估计出值。

步骤4：根据估计偏差曲线对μ值进行修正：

图6 信号FFT及频谱包络示意图Fig.6 Envelope of signal′s spectrum after FFT

步骤5：根据式（14）获得精确的频率和相位估计值。

4 算法的仿真与分析

仿真采用数据辅助并假定信号已经过准确位定时同步，观测数据长度为128个符号，每个数据点做5 000次独立试验。

图7为Es／N0为2dB数据辅助条件下，输入信号频率变化时，本文算法采用方案1与Rife，Quinn，三线幅度法（文献［7］）及A＆M算法（文献［10］）的频率和相位估计仿真曲线。可以看出，频率估计方面，Rife性能最差、Quinn算法次之；本文算法方案1与A＆M算法性能非常接近，均逼近CRB界，但A＆M算法需要多次迭代，运算量和处理延迟均显著超过方案1；三线幅度法性能略差于方案1，且其FFT运算长度为方案1的两倍。相位估计方面，方案1和三线幅度法性能接近，均显著优于Rife算法。

图8为本文算法的方案1、方案2及三线幅度法的频率和相位估计仿真曲线。可以看出，对于频率估计，本文算法的方案1性能最优；方案2随着窗口长度参数I的增大，估计误差逐渐缩小，当I＝6时其性能已经非常接近于方案1；三线幅度法误差介于方案2的I＝1和I＝2曲线之间。对于相位估计，除了I＝1的方案2外，其余曲线的最大误差非常接近。

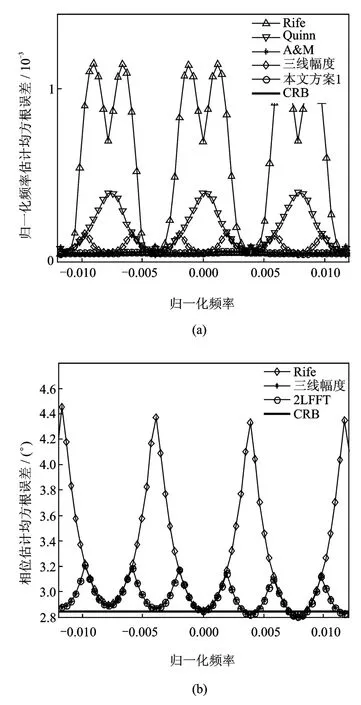
图7 本文方案1与Rife，Quinn，A＆M、三线幅度算法的频率和相位估计仿真图Fig.7 Frequency and phase simulation curves of first proposed scheme Rife，Quinn，A＆M，algorithm of 3spectrum′s amplitudes

图9给出了各种信噪比条件下，本文算法方案2的频率和相位估计仿真结果。可以看出，L＝128，I＝6时频率和相位估计所需的信噪比门限均低于－4dB，适合于极低信噪比条件下信号的接收，同时估计性能也非常逼近CRB界。

表1比较了各频域类载波估计算法的性能和运算量。

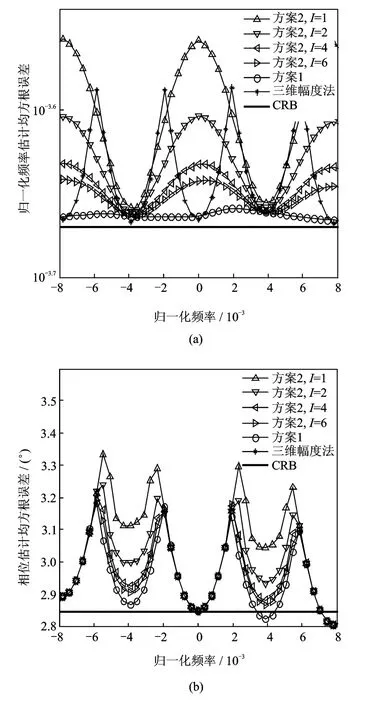
图8 本文方案1、方案2与三线幅度算法的频率和相位估计仿真图Fig.8 Frequency and phase simulation curves of first proposed scheme，second proposed scheme，algorithm of 3spectrum′s amplitudes

表1 各频域类载波估计算法比较（仿真条件：Es／N0＝2dB，L＝128，频差为0）Table 1 Comparison of frequency－domain－type carrier estimation algorithms（Simulated at L＝128，Es／N0＝2dB with no frequency offset）

本文算法及其实现方案可广泛应用于各类数字接收机中，对改善载波同步精度和提高接收机性能具有重要现实意义。由于所需的信噪比门限低（如图9所示的信噪比门限低于－4dB），本文算法及其实现方案能很好地满足低信噪比条件下通信的要求，应用前景广阔。

图9 简化实现方案（I＝6）的频率和相位估计仿真图Fig.9 Frequency and phase simulation curves of simplified scheme（I＝6）

5 结束语

本文提出了基于三角多项式插值的频率和相位联合估计算法，并给出了对应的实现方案1和方案2。本文方案1具有最优的性能，估计精度非常逼近CRB界。方案2频率和相位估计精度仅略差于方案1，但非常逼近，其主要优势是运算量约减少了一半。与三线幅度法和A＆M算法相比，方案2估计精度与其基本相当，但运算量仅约为其一半，优势明显。

［1］Fitz M P.Planar filtered techniques for burst mode carrier synchronization［C］／／IEEE GLOBECOM′91.Phenix，AZ：IEEE，1991：365－369.

［2］Mengali U，Morelli M.Data－aided frequency estimation for burst digital transmission［J］.IEEE Trans Comm，1997，45（6）：23－25.

［3］齐国清，吕健.基于自相关函数相位的频率估计方法方差分析［J］.大连海事大学学报，2007，33（4）：5－9.Qi Guoqing，Lv Jian.Variance analysis on sinusoid frequency estimators based on the argument of the sample autocorrelation function［J］.Journal of Dalian Maritime University，2007，33（4）：5－9.

［4］Rife D，Boorstyn R.Single－tone parameters estimation from discrete－time observations［J］.IEEE Trans Inform Theory，1974，20（9）：591－598.

［5］Hong D K，Kim D J，Lee Y J.A simple interpolation technique for the DFT for joint system parameters estimation in burst MPSK transmissions［J］.IEEE Trans Comm，2003，51（7）：1051－1056.

［6］Quinn B G.Estimating frequency by interpolation using Fourier coefficients［J］.IEEE Trans，1997，28（2）：113－122.

［7］龚超，张邦宁，郭道省.基于FFT的快速高精度载波参数联合估计算法［J］.电子学报，2010（4）：766－770.Gong Chao，Zhang Bangning，Guo Daoxing.A quick and accurate union carrier parameter estimation algorithm based on FFT［J］.Acta Electronica Sinica，2010（4）：766－770.

［8］罗武，刘安，梁庆林.一种迭代频偏估计算法［J］.北京大学学报：自然科学版，2008，44（4）：554－558.Luo Wu，Liu An，Liang Qinglin.An iterative carrier frequency estimation algorithm［J］.Acta Scientiamm Naturalism Universitatis Pekinese，2008，44（4）：554－558.

［9］Reisenfeld S，Aboutanios E.A new algorithm for the estimation of the frequency of a complex exponential in additive Gaussian noise［J］.IEEE Trans Letters，2003，7（11）：549－551.

［10］Aboutanious E，Mulgrew B.Iterative frequency estimation by interpolation on Fourier coefficients［J］.IEEE Trans Signal Processing，2005，53（4）：1237－1242.

［11］Minhas S，Aboutanious E.Estimation of the frequency of a complex exponential［C］／／IEEE ICASSP.Las Vegas，NV：［s.n.］，2008：3693－3696.

［12］邓阵淼，刘渝，王志忠.正弦波频率估计的修正Rife算法［J］.数据采集与处理，2006，21（6）：473－477.Deng Zhenmiao，Liu Yu，Wang Zhizhong.Modified Rife algorithm for frequency estimation algorithm of sinusoid wave［J］.Journal of Data Acquisition and Processing，2006，21（6）：473－477.

［13］陈役涛，刘渝，邓阵淼.基于相关累加的正弦波频率估计算法［J］.数据采集与处理，2008，23（4）：729－733.Chen Yishou，Liu Yu，Deng Zhenmiao.Frequency estimation algorithm of sinusoid wave based on correlative accumulation［J］.Journal of Data Acquisition and Processing，2008，23（4）：729－733.

［14］王宏伟，赵国庆，齐飞林.一种实时精确的正弦波频率估计算法［J］.数据采集与处理，2009，24（9）：208－211.Wang Hongwei，Zhao Guoqing，Qi Feilin.Real－time and accurate single frequency estimation approach［J］.Journal of Data Acquisition and Processing，2009，24（9）：208－211.

［15］吴桂波，张立军，鲁辉，等.基于多段信号融合的实时高精度频率估计算法［J］.数据采集与处理，2012，27（3）：578－582.Wu Guibo，Zhang Lijun，Lu Hui，et al.A real－time and high－precision algorithm for frequency estimation by fusing multi－section signals［J］.Journal of Data Acquisition and Processing，2012，27（3）：578－582.

［16］Fu D，Willson A N.Trigonometric polynomial interpolation for timing recovery［J］.IEEE Transactions on Circuits and Systems－I Regular Papers，2005，52（2）：289－295.

［17］Ye Zhan，Xu Guangfei，Guo Daoxing.An accurate estimation algorithm of frequency and phase at low signal－noise ratio levels［C］／／2010International Conference on Wireless Communications ＆ Signal Processing.Suzhou，China：［s.n.］，2010：482－486.