一种新型非调节隔离DC-DC变换器
陈章勇 许建平 王金平 张 斐
(西南交通大学电气工程学院 成都 610031)
1 引言
近年来,高功率密度、高效率已成为开关变换器追求的目标。随着开关频率的提高,传统硬开关PWM 变换器的开关损耗急剧增大,导致开关变换器效率的降低,限制了开关变换器开关频率和功率密度的进一步提高。软开关技术可以实现开关管的零电压开通或零电流关断,减小了开关损耗,提高了变换器的效率和功率密度。因此,软开关变换器越来越受到人们的重视。
开关变换器可分为可控变换器和不可控变换器,可控变换器一般通过脉冲宽度调制或脉冲频率调制实现输出电压的控制;不可控变换器,又称为DC-DC变压器(DCX),表现为直-直变压器的特性,输入输出电压传输比与负载、开关频率和占空比无关,可将变换器设计在最佳工作点,获得较高的效率[1-6]。
在分布式电源架构中,通常采用 DCX变换器作为中间母线变换器[7]。文献[7]研究了利用变压器二次漏感与输出电容进行谐振,获得同步开关管的ZCS,消除同步开关管的体二极管的导通损耗;同时,采用自驱动方案,减小了同步开关管的驱动损耗,提高了变换器的效率。为了进一步提高变换器的效率,文献[8-11]研究的并联功率处理方案均采用了DCX变换器,以获得高效率DC-DC变换器。
本文提出了一种新型隔离 DCX变换器,该变换器的隔离变压器一次侧为带隔直电容的不对称半桥(Asymmetric Half-Bridge, AHB),变压器二次侧为串联双谐振电路。该变换器利用励磁电感电流获得一次开关的零电压开通,同时,由变压器二次漏感和谐振电容组成的回路[12,13]实现了二极管的零电流关断,消除了二极管的反向恢复损耗,同时减小了二极管的电压应力。变压器一次侧采用半桥结构,开关管的电压钳位在输入电压,减小了开关管的电压应力,可通过选择较低导通电阻的MOSFET,以减小导通损耗。二次侧二极管的电压钳位在输出电压,不受占空比的影响。本文详细分析了该变换器的工作模式,进行了稳态分析,并给出了变换器的软开关实现条件。最后,通过一个72W输出功率,48V输入、12V输出的DC-DC变换器实验电路验证了理论分析的正确性。
2 二次侧谐振AHB变换器拓扑的提出
如图1a所示AHB-Forward变换器的二次侧为Forward结构[14],AHB-Forward变换器的输出端存在电感,二极管桥臂为电感提供续流回路。当二极管桥臂换流时,桥臂二极管均导通,换流期间存在较大的损耗。此外,二极管的寄生电容与变压器二次漏感谐振,造成较严重的振荡现象[7],需要采用吸收电路来解决这一问题;同时,半桥变换器工作于不对称脉冲调制(Asymmetric Pulse Width Modulation, APWM)模式时,二次侧二极管的电压应力与占空比有关,造成输出端二极管的电压应力不平衡,在实际应用时限制了其应用。
基于二次侧谐振的思想,本文提出了如图 1b所示的二次侧谐振 AHB变换器,在一定条件下不仅实现了二极管的零电流关断,而且二次侧不需要滤波电感,减小了变换器的成本及体积,有利于变换器小型化和轻量化。同时,二极管的电压应力均钳位在输出电压,其电压应力与占空比无关,不会造成二极管电压应力的不平衡。

图1 不对称半桥变换器拓扑电路Fig.1 Topology of asymmetric half-bridge converter
3 二次侧谐振AHB变换器分析
为了简化该二次侧谐振 AHB变换器的分析,做如下假设:
(1)开关管S1和S2工作于APWM模式,且存在一定的死区时间,开关管S1的占空比为D。除反并联二极管与输出电容外,开关管 S1和 S2是理想的。
(2)变压器模型由n:1的理想变压器、励磁电感Lm和一次、二次漏感Lr1、Lr2组成;励磁电感Lm远远大于漏感Lr1。
(3)输出电容 Co足够大,认为输出电压 Vo恒定不变;隔直电容Cb上的电压恒定。
(4)谐振电容 Cr1和 Cr2具有相同的电容值(Cr1=Cr2=Cr)。
(5)变换器工作于稳态。
由于输出电容足够大,可以忽略输出电压纹波,则流过输出端谐振电容的电流为

此外,输出电流等于二次侧谐振电流的一半,即

在分析变换器的工作模式之前,需要首先讨论二次侧谐振频率(由二次侧漏感与谐振电容构成的谐振回路)对变换器工作模式的影响,这也是实现二极管VD1、VD2零电流关断的关键因素。
3.1 二次侧谐振频率设计
图2所示为二次侧谐振频率对变压器二次电流工作模式的影响。采用APWM调制,开关管S1的导通时间为DTs,开关管S2的导通时间为(1-D)Ts,Ts为开关周期。谐振周期为Tr=,谐振频率 fr=1/Tr。二次侧谐振频率与开关频率之间,存在三种情况:①Tr/2<DTs,在这种情况下,变压器二次电流为两个正弦半波,且存在电流为零的自由工作模态;②DTs<Tr/2<Ts–DTs,在开关管 S2导通期间存在正弦半波,而开关管S1导通期间,电流为正弦状,造成了占空比的丢失;③Tr/2>Ts–DTs,两个半波均为正弦波的一部分。为了实现二极管的软开关,消除二极管的反向恢复损耗,本文研究第一种情况,即

式中,fs为开关频率,fs=1/Ts;Deff为有效占空比。

图2 二次侧谐振频率对变压器二次电流工作模式的影响Fig.2 Influence of resonant frequency of transformer secondary side on the operation of the converter
3.2 工作模式分析
在一个开关周期内,变换器存在如图3所示的8种工作模态,如图4a和图4b所示分别为变压器一次侧主要波形和二次侧主要波形。在开关周期开始时刻,二次电流is为零,变压器一次电流ip为负。



图3 变换器工作模态及等效电路Fig.3 Operation modes and equivalent circuits of the proposed converter

图4 变换器关键波形Fig.4 The key waveforms of converter primary side(a)and secondary side(b)
模态1[t0~t1]:t0时刻,变压器二次电流is为零,变压器一次电流ip等于励磁电感电流im,且为负值,开关管S1的反并联二极管导通,为励磁电感电流提供流通路径。变压器二次侧二极管VD1导通,形成谐振回路。励磁电感电压等于Vdc–VCb,励磁电感电流im线性上升。
模态 2[t1~t2]:t1时刻,开关管 S1导通,励磁电感Lm两端电压等于Vdc–VCb,励磁电感电流im线性上升;变压器二次侧二极管VD1导通,VD1为二次漏感 Lr2和谐振电容 Cr1提供回路,二极管 VD2电压钳位在输出电压。谐振电容电压vCr1上升,vCr2下降。由于漏感 Lr1远小于励磁电感 Lm,漏感 Lr2上的电压忽略不计。在此期间,励磁电感电流为
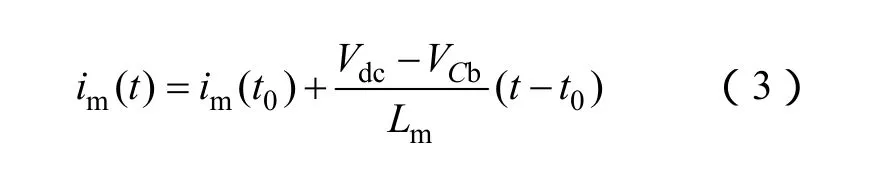
变压器二次侧Lr2和Cr1谐振,由图3中工作模态1和工作模态2的等效电路,可以得到

器二次电流is的峰值电流。
一次电流ip为励磁电感电流与二次侧折算到一次电流之和,可表示为

模态3[t2~t3]:t2时刻,流过二极管的电流iVD1变化到零,二极管VD1实现零电流关断。谐振电容Cr1、Cr2上的电压保持不变,并与输出电容Co并联为负载提供能量。此时,开关管S1继续导通,一次电流ip等于励磁电感电流im,线性上升。此阶段时间 t2–t0=Tr/2。
模态 4[t3~t4]:t3时刻,开关管 S1关断,由于励磁电感较大,励磁电感电流可认为保持不变,开关管的输出电容Cs1和Cs2分别充电和放电。由于电容Cs1和Cs2较小,励磁电感电流较大,此阶段工作时间极短。
模态 5[t4~t5]:t4时刻,开关管 S1的输出电容电压充电到 Vdc,开关管 S2的反并联二极管导通,为励磁电感电流im提供通路,为开关管S2的零电压开通创造了条件。在此阶段,隔直电容Cb上的电压加到励磁电感Lm上,变压器一次电压vp等于–VCb,im线性减小。一次电压折算到二次侧时,迫使二极管VD2导通,二次侧形成谐振回路。此时,一次电流流过开关管S2的反并联二极管。
模态 6[t5~t6]:只要开关管 S2在 t5时刻之前开通,均可以实现开关管S2的ZVS开通。t5时刻,一次电流ip过零变负,一次电流流过开关管S2,励磁电感电流 im线性下降。变压器二次侧二极管 VD2继续导通,形成谐振回路。谐振电容电压vCr1下降,vCr2上升。由图3中工作模态5、6的等效电路,可以得到
模态7[t6~t7]:t6时刻,流过二极管的电流iVD2变为零,二极管 VD2实现零电流关断。谐振电容Cr1、Cr2上的电压保持不变,并与输出电容Co并联为负载提供能量。此时,开关管S2继续导通,一次电流ip等于励磁电感电流im,线性下降。
模态 8[t7~t8]:t7时刻,开关管 S2关断,由于励磁电感较大,励磁电感电流可认为保持不变,开关管的输出电容Cs1和Cs2分别放电和充电。由于电容Cs1和Cs2较小,励磁电感电流较大,此阶段工作时间也极短。当开关管 S2的输出电容电压充电到Vdc时,开关管 S1的反并联二极管导通,为开关管S1的零电压导通创造了条件,进入下一个开关周期。
4 稳态特性分析
由工作模式分析可知,工作模态4和模态8的工作时间极短,在进行稳态特性分析时,忽略死区时间和占空比丢失对变换器工作特性的影响。根据励磁电感Lm的伏秒平衡,可得


在分析变换器的输入输出电压增益比之前,首先分析谐振电容电压最小值和最大值之间的关系。由图 4b中变压器二次侧主要波形可知,就谐振电容电压vCr1、vCr2而言,稳态工作时,开关周期结束时刻的电压等于开关周期开始时刻的电压,且谐振电容电压满足vCr1(t)+ vCr2(t)=Vo。
工作模态1~2和工作模态5~6的工作时间等于半个谐振周期(Tr/2),由式(14)可得

联立式(18)~式(20),解得

对于工作模态1~2,由式(8)和图4b的主要
工作波形可得
由式(27)可得,二次侧峰值电流为


代入峰值电流Is,peak的表达式,可得

由式(29)、式(30)和图4b中谐振电容电压波形可知,在一个开关周期内,谐振电容两端的平均电压为
由式(17)、式(21)、式(24)和式(25)联立解得变换器输入输出电压增益比


且由式(3)可得励磁电感电流峰值Im为
由式(26)可知,此变换器表现出 DCX的增益特性,输入、输出电压传输比与开关频率、占空比和负载无关。
在电压增益表达式的基础上,进一步分析谐振电感峰值电流Is,peak1与Is,peak2之间的关系。由式(7)和式(13)中Is,peak1、Is,peak2的表达式可知,并将式(21)、式(26)代入其表达式得

5 DCX的实现条件及软开关条件

5.1 DCX二次侧谐振实现条件
由前面的工作模式分析可知,要实现 DCX变换器的特性,需满足以下条件:
(1)在一个开关周期内,二次侧谐振电流存在两个完整的正弦半波,可实现二极管的零电流关断,即需要满足式(2),如图2所示。为了简化计算,认为有效占空比Deff=D。因此
由式(27)可知,变换器二次电流波形关于时间轴对称,同时也优化了输出电流的峰值电流,减小了输出电容的电流纹波。
只有在二次侧形成谐振回路时,变换器才能通过变压器一次侧向负载传送能量。由图4b的工作波形可知,在一个开关周期内,输出电流的平均值为

(2)由图4b可知,谐振电容电压始终大于零,即谐振电容电压满足


联立解得

为了满足式(34)和式(37),变压器二次漏感需满足

5.2 DCX变换器一次侧软开关实现条件
从工作模态分析可以看出,设计励磁电感时,为了实现一次侧开关S1、S2的零电压开通,需要励磁电感存储的能量足以提供Cs1和Cs2充放电所需能量。在死区时间内,励磁电感电流的峰值对开关管的结电容放电,所以满足不等式

由式(33)可知,励磁电感选得过大,将导致励磁电感电流峰值Im较小。励磁电感电流减小,开关管的关断电流减小,从而减小开关管的关断损耗,如图4a所示。当励磁电感电流很小时,可认为实现了开关管的零电流关断,此时进一步提高了变换器的效率。然而,励磁电感电流过小,为满足式(40),励磁电感很大。所以,最佳方案是取Im=2CossVdc/tdead,代入式(33),可得励磁电感应满足

式中,Coss=Cs1=Cs2,tdead为驱动脉冲的死区时间。
6 实验验证
根据软开关实现条件,选取实验参数见下表。取占空比D=0.4,负载电阻R=2Ω,实验中的关键波形如图5所示。
图 5a为变换器的开关管电压波形和变压器一次电流波形,由图可知开关管 S1和开关管 S2导通时刻,其电流均为负,致使其反并联二极管导通,将其电压钳位在零,实现了开关管S1、S2的ZVS。且励磁电感电流较小,开关管的关断电流较小,如图5a所示,近似实现了开关管的零电流关断。由变压器一次电流波形可知,在开关管关断之前,励磁电感电流等于一次电流,即二次侧二极管电流为零,实现了二次侧二极管的零电流关断。图5b为变压器二次侧的关键波形,二极管电压钳位在输出电压,谐振电容电压始终大于零,与理论分析一致,验证了参数选取的正确性。同时,证明了该变换器的可行性。

表 变换器参数Tab. Parameters of converter

图5 变换器主要实验波形Fig.5 The key waveforms of the converter
图6为变换器的实测增益曲线,其中虚线为输出电压与输入电压理想增益比。由图6可知,变压器的增益比基本上符合 DCX变换器的增益特性。如图7所示为变换器随输出功率变化的效率曲线,可知变换器具有较高的效率。

图6 变换器的增益曲线Fig.6 Transfer gain curve of the converter

图7 变换器的效率曲线Fig.7 Efficiency curve of the converter
7 结论
本文研究了一种新型隔离非调节 DC-DC变换器,利用 APWM调制策略实现了开关管的 ZVS,二次侧谐振电路实现了二极管的ZCS。同时,几乎可以实现开关管的零电流关断。与传统 AHB变换器相比,该变换器拓扑消除了输出滤波电感,输出二极管电压钳位在输出电压,减小了二极管的电压应力,且表现出 DCX变换器的特性,输入输出增益比与负载、开关频率和占空比无关。
[1] Ivensky G, Abramovitz A, Gulko M, Ben-Yaakov S.A resonant DC-DC transformer[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(3):926-934.
[2] Xianjin Zhang, Caihong Fan. Research on a novel DC-DC transformer[C]. In proceeding of IEEE Electric Information and Control Engineering, 2011: 1619-1622.
[3] Gonzalez M C, Alou P, et al. DC-DC transformer multiphase converter with transformer coupling for two-stage architecture[C]. Proceeding of IEEE Applied Power Electronics Conference, 2010: 781-786.
[4] Abramovitz A. Smedley K. A resonant DC-DC transformer with zero current ripple[C]. Proceeding of IEEE Power Electronics Specialist Conference (APEC),2005: 1299-1305.
[5] Zhilei Yao, Lan Xiao, Yangguang Yan. A family of zero voltage switching DC-DC transformers[C]. Proceeding of IEEE Applied Power Electronics Conference(APEC), 2006: 513-516.
[6] Weiyi Feng, Paolo Mattavelli, Fred C Lee. Pulsewidth locked loop(PWLL) for automatic resonant frequency tracking in LLC DC-DC transformer (LLCDCX)[J]. IEEE Transactions on Power Electronics,2013, 28(4): 1862-1869.
[7] Yuancheng Ren, Ming Xu, Julu Sun, et al. A family of high power density unregulated bus converters[J].IEEE Transactions on Power Electronics, 2005, 20(5):1045-1054.
[8] Julu Sun, Ming Xu, Reusch D, et al. . High efficiency quasi-parallel voltage regulators[C]. In Proceeding of IEEE Applied Power Electronics Conference, 2008:811-817.
[9] Ming Xu, Ya Liu, Julu Sun, Lee F C. Σ/sigma DC/DC conversion for computing and telecom applications[C]. Proceeding of IEEE Power Electronics Specialist Conference, 2008: 1190-1195.
[10] Pengjie Lai, Julu Sun, Lee F C. Control scheme and transient performance of sigma VR[C]. In Proceeding of IEEE Applied Power Electronics Conferenc, 2010:1927-1933.
[11] Ejea J B, Ferreres A, Sanchis-Kilders E, et al. Optimized topology for high efficiency battery discharge regulator[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1511-1521.
[12] Ki-Bum Park, Chong-Eun Kim, Gun-Woo Moon, et al.PWM resonant single-switch isolated converter[J].IEEE Transactions on Power Electronics, 2009, 24(8):1876-1886.
[13] Jong-Jae Lee, Jung-Min Kwon, Eung-Ho Kim, et al.Dual series-resonant active-clamp converter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(2):699-710.
[14] Yi-Hsin Leu, Chern-Lin Chen, Tso-Min Chen. Analysis and design for asymmetrical half-bridge forward mode converters[C]. Proceeding of IEEE Power Electronics and Drive Systems, 2001: 126-130.

