基于滞后补偿的PWM 逆变器控制策略研究

刘宝其 段善旭 陈昌松 方支剑

（强电磁工程与新技术国家重点实验室（华中科技大学）武汉 430074）

1 引言

大功率储能系统的建设离不开功率调节系统（Power Conditioning System,PCS）的研究。储能系统中的PCS 一般采用双向高频PWM 变换器加双向直流变换器构成双级式能量变换系统，或直接采用双向高频PWM 变换器加相应的直流滤波电感构成能量变换系统，根据用户需求变换器可以工作于并网状态或者离网状态[1-3]。当PCS 离网运行时，其工作特性与逆变器一致，针对其输出波形控制技术，国内外学者提出许多优良的数字控制方法，主要包括单闭环PID 控制、双闭环控制、无差拍控制、重复控制、状态反馈控制、滑模变结构控制、微分平滑控制和基于模糊控制和神经网络控制的智能控制等算法[4-10]。其中单闭环控制算法简单、鲁棒性强，但对非线性负载适应较弱；重复控制能够消除周期性的扰动影响而获得较好的输出电压波形，但是动态响应速度较慢[11]；状态反馈法一般只针对空载建立，需对负载扰动采取针对性的措施[12]；而智能控制算法则通常需要进行复杂的运算，运用相对较少。

基于极点配置的双闭环设计具有很好的控制性能，传统的极点配置为求简便，一般基于连续域进行设计，被控对象为二阶模型，根据“控制参数量与控制自由度相等的原则”，此时可以任意配置系统的极点以获得期望的动态响应特性[13,14]。但是采用数字控制时，由于采样、计算延时限制了系统输出占空比，甚至会引起系统的不稳定。为了防止占空比受限，通常采用滞后一拍控制，从而使逆变器控制对象由原来的二阶系统升高为三阶，此时控制系统不再满足极点配置的条件了。文献[15,16]分别通过在对象建模时考虑延时和提前时刻采样，解决了占空比受限的问题。文献[17]采用观测器预测系统的状态变量，消除滞后一拍的影响，然而由于系统模型误差和建模误差的影响存在较大的预测误差。文献[18]在观测器中加入重复控制补偿预测误差，取得较好的稳态和动态性能，却增加了控制系统的复杂度，降低了系统稳定性，尤其是针对三相系统需用到的状态观测器数目较多，在开关频率较高的系统这是难以接受的。

为此，本文通过分析了离散域下逆变器控制参数量与系统阶数的关系，引入控制器输出量作为系统状态变量，并引入相应的反馈系数，使得离散化后系统的控制自由度增加一个，从而满足任意配置极点的条件。分析表明，系统引入新状态变量且采用双环控制策略时，内、外环控制器可以选择P控制器、PI 控制器、PD 控制器或者PID 控制器的任意组合，通过配置不同的反馈系数均可获得良好的动态性能，并且该方法具有简单可靠、方便实现的特点。最后，本文设计了基于增广状态变量的电感电流内环、电容电流外环的双环控制策略，仿真和实验表明该方法具有良好的动静态特性。

2 PWM 逆变器模型

图1为三相逆变器的主电路图，交流侧为LC滤波器，rL为考虑逆变器滤波电感L 内阻、死区效应、开关管导通压降和线路阻抗等各种阻尼因素的综合等效电阻，Zload表示系统负载（输出通过一个180:380 的D11Yn 型变压器连接负载，图1 中未画出），逆变器的关键参数见表1。

图1 三相逆变器主电路结构图Fig.1 Main circuit of a three-phase inverter

由图1 可知，假设开关管均为理想器件，建立三相静止坐标系下的系统模型，并转换到同步旋转坐标系下（假设已完成dq 轴之间的解耦），则可建立d 轴分量在连续域下的状态空间表达式如式（1）所示，其连续域模型则如图2 所示（q 轴分析与d轴类似）。

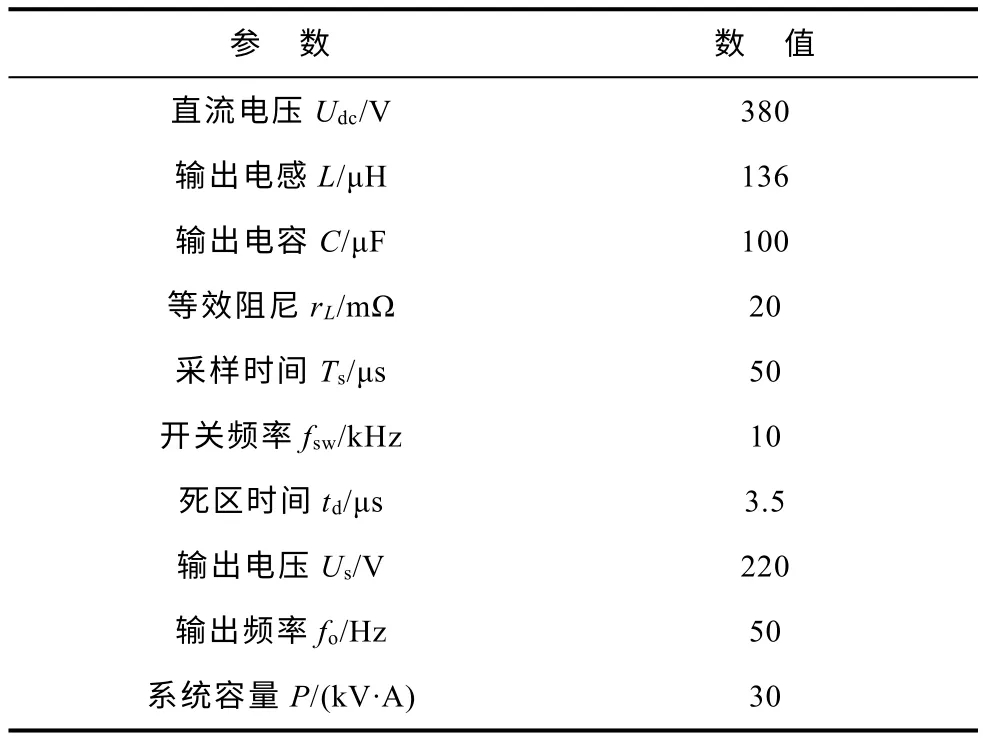
表1 逆变器电路的关键参数Tab.1 Key Parameters of the inverter

图2 逆变器系统连续域模型Fig.2 Inverter model in continuous domain

图2 中，vr为数字控制器的输出量，经过零阶保持器实现数模转换后作用于逆变器系统。由于采用直接数字化设计可以在保证系统稳定性的同时获得更宽的控制带宽，因此被广泛运用。假设系统采样时间均为Ts，则由式（1）可推出离散域下，电感电流iL到逆变器端口电压v1的传递函数为

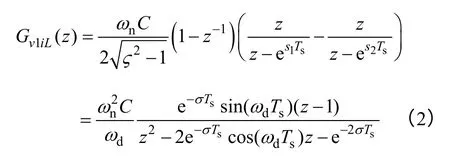
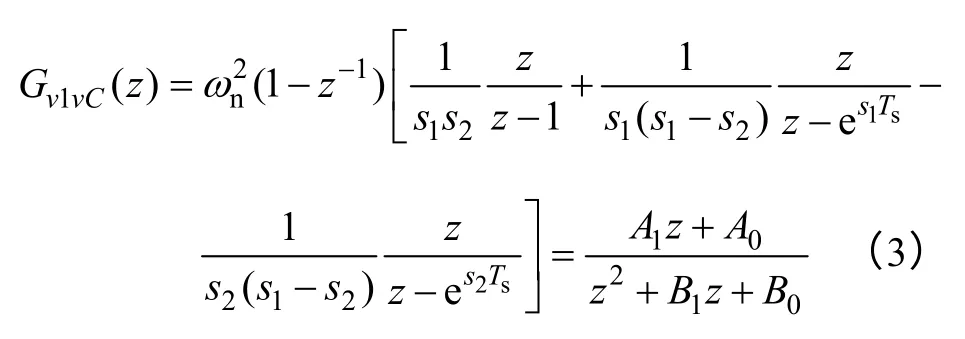
电感电流iL到电容电压vC的传递函数为

式中

则由式（3）～式（5）可得出逆变器系统离散域模型如图3 所示，KPWM为逆变器的桥臂增益，并对各反馈系数进行归一化处理。

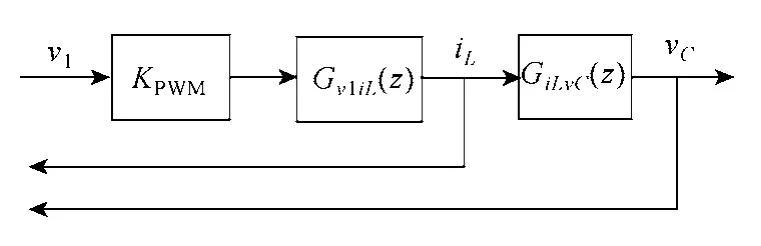
图3 逆变器系统离散域模型Fig.3 Inverter model in discrete domain

3 基于滞后补偿的控制策略

3.1 控制参数量与控制自由度关系

从前节的建模分析可知，基于LC 滤波器的逆变器，不论单环结构还是双环结构（电感电流内环或者电容电流内环），在未加控制器且采用滞后一拍控制时，其闭环传递函数可表示为

可见，滞后一拍环节的引入使得逆变器离散域模型增加为3 阶，代表系统的3个被控自由度。在此基础上，如果引入控制环节，则采用不同的离散化方法可以得到控制参数（可控自由度）与系统阶数（被控自由度）的关系见表2（采用双环控制策略，且双环均为同类型的控制器）。

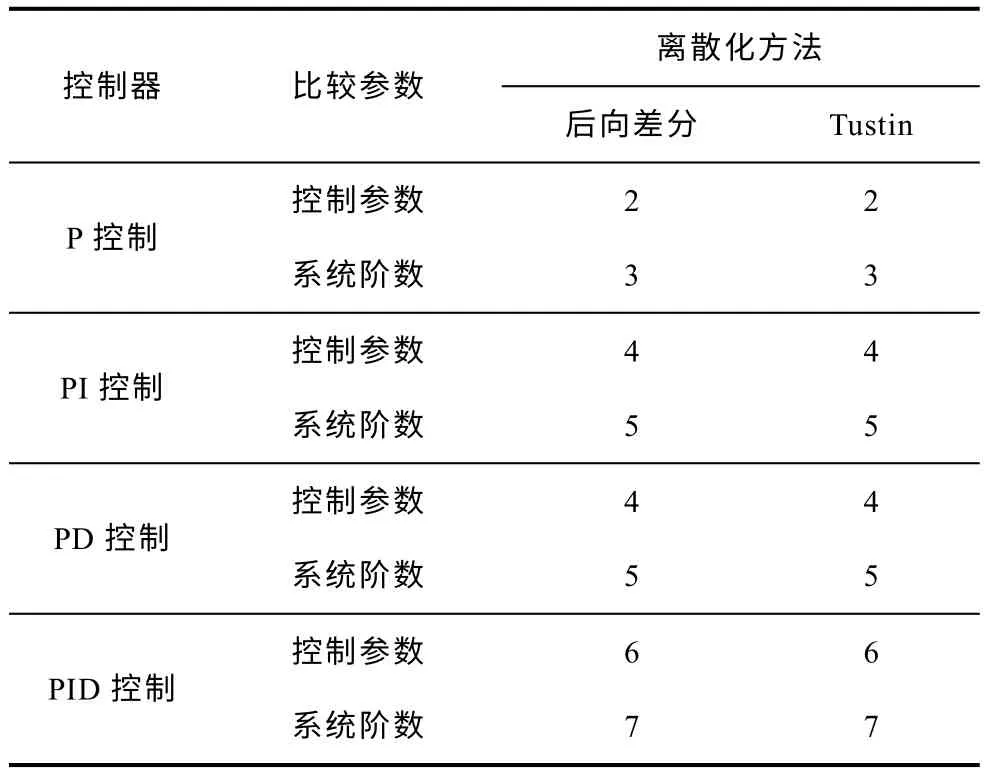
表2 考虑滞后一拍时，控制参数与系统阶数的关系Tab.2 The relationship between DOF of controller and DOF of system when one-step-delay is considered

由表2 可知，离散化逆变器系统引入滞后一拍控制环节后，系统的可控自由度和被控自由度始终相差为1。同理，当内、外双环采用不同类型控制器，或者采用其他离散化方法时也可以得到相同的结论。

3.2 增广状态变量的选取和分析

文献[13]指出系统的控制参数量（可控自由度）与系统阶数（被控自由度）相等是高性能逆变器控制实现的基础，也是实现系统极点任意配置的条件，因此，需要为系统增加一个可控自由度。针对逆变器系统，可选取电感电流、电容电流、电容电压三者的积分或者微分环节为新的状态变量。但是，在引入前述几种状态变量的同时也增高了系统的阶数，仍然不满足“控制器可控自由度与系统被控自由度相等”的约束条件。为此，本文引入控制器的输出量vr为增广状态变量，并引入Kz为其反馈系数，以构建新的逆变器离散域模型，其控制框图如图4 所示。

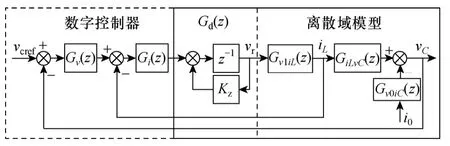
图4 基于增广状态变量的控制框图Fig.4 Control block based on augmented state-variable

图4 中，对KPWM和各采样通道的反馈系数进行了归一化处理，故均略去；z-1表示系统采用滞后一拍控制；Gv(z)和Gi(z)分别为电容电压外环和电感电流内环的控制器；Gi0vC(z)为系统的闭环输出阻抗；Gd(z)则表示由增广状态变量构成的新环节，对于离散系统，它既由控制器实现，同时也属于离散域模型的一部分。

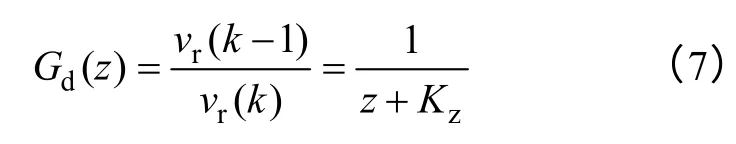
其等效于对滞后一拍环节进行了修正，画出Kz变化时Gd(z)的Bode 图如图5 所示，且由式（7）可得Gd(z)的相频特性为

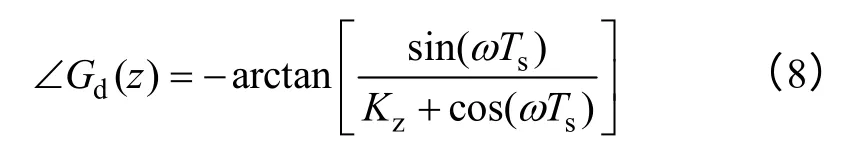
由图5 和式（8）可知

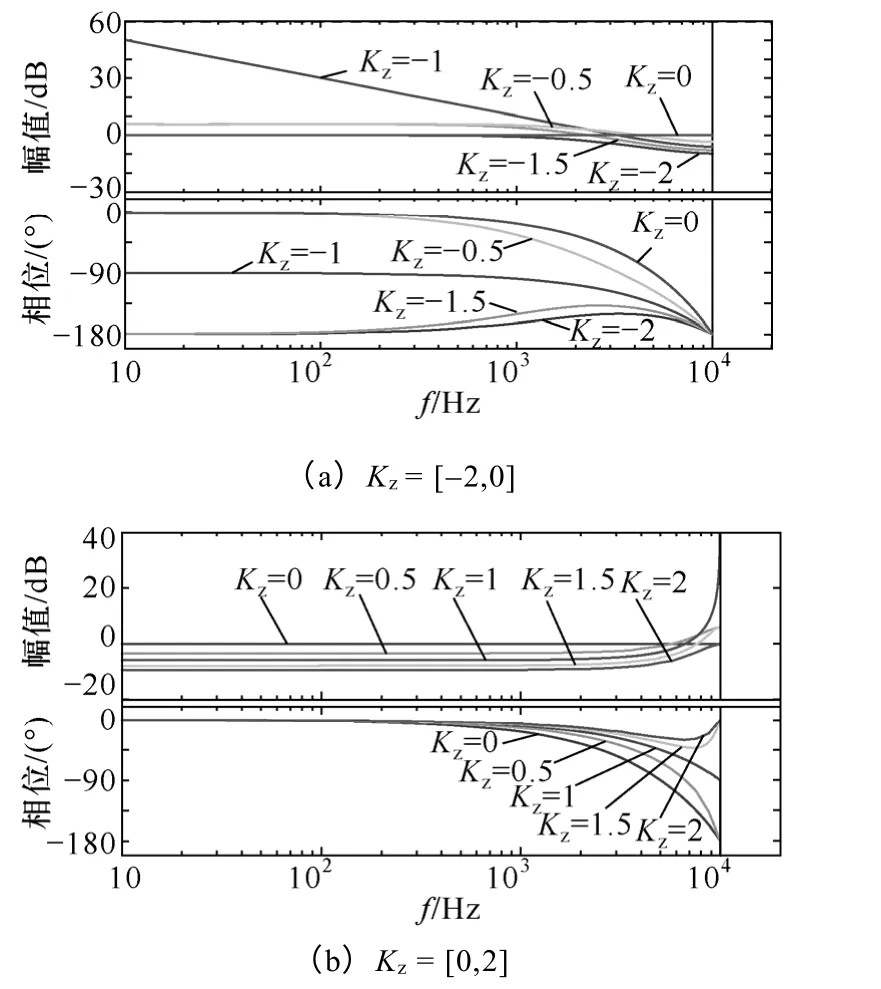
图5 延时环节的Bode 图Fig.5 Bode diagram of delay link

（1）当Kz=[-2,0)时，延时环节引入的极点位于z 域的右半平面，且随着极点的右移，Gd(z)产生的相位滞后越大，尤其是当极点右移至单位圆外后，其引入的低频段相位滞后超过90°，这对原本存在相位滞后的二阶逆变器系统是极为不利的，特别是采用传统的PI 控制时，控制器本身还会引入相位滞后，因此Kz＜0 的情况不予考虑。

（2）当Kz=0 时，延时环节退化成滞后一拍环节，其引入的相位滞后为(360fTs)°，在1kHz 处引入的相位滞后达18°，极大地降低了系统的稳定裕度，尤其是对开关频率较低的大功率逆变器系统，其引入的相位滞后更为严重。

（3）当Kz=（0,2]时，延时环节引入的极点位于z 域的左半平面，且随着极点的左移，Gd(z)产生的相位滞后越小。需要注意的是，当极点左移至单位圆外后，其引入的低频段相位滞后进一步减小，并在高频段转为上升使得乃奎斯特频率处的相位滞后减为0，即∠Gd(z)|ω=π/Ts=0。

同样，Gd(z)的幅频特性可表示为

在ω=(0,1/(2Ts))范围内，|Gd(z)|单调递增，且随着Kz的增大，|Gd(z)|减小。当Kz=2 时，直流分量的幅值增益比滞后一拍控制时降低9.54dB，但是可以很方便地通过控制器对其增益进行补偿。因此，可以通过选取Kz为合适的正数用于补偿滞后一拍控制产生的相位滞后，并通过式（8）和式（9）分别计算出其对应的相位和幅值，然后进行控制器的时域设计。此种设计方法，可以精确地计算出控制器需要补偿的相位和幅值，有利于提升系统的控制带宽，提高系统动态性能。

3.3 基于极点配置的双闭环控制策略

为了优化系统的动态特性，本文采用极点配置法对图4 所示的控制系统进行参数设计。分别求出电感电流内环的开环和闭环传递函数、电容电压外环的开环和闭环传递函数、系统闭环输出阻抗的传递函数，如下所示。

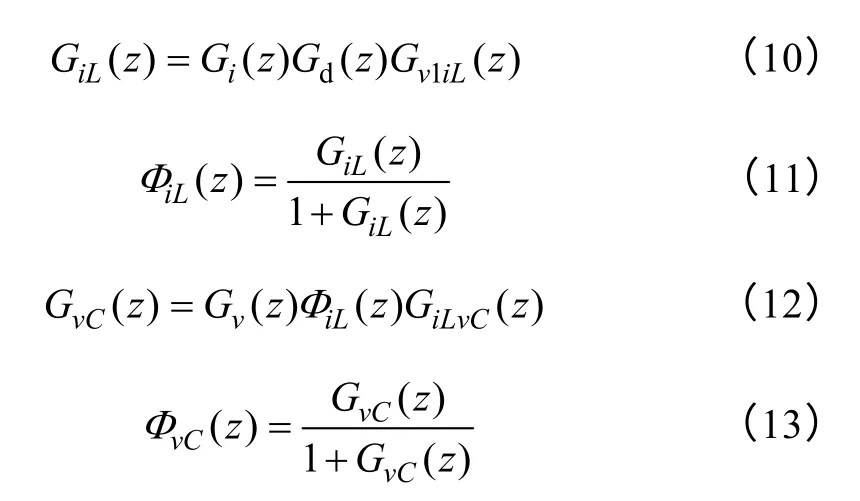
由图4 可知，输出电压同时受ΦvC(z)和Gi0vC(z)的影响，为了保证系统的稳态精度和鲁棒性，本文设计的控制器内、外环均采用PI 补偿器，即

则由式（13）可求出逆变器系统的特征方程为

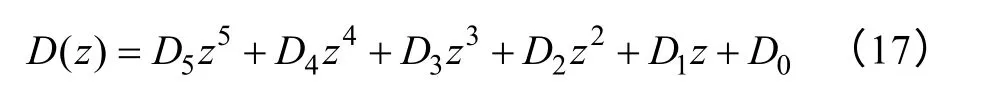
式中，Di(i=0,1,···,5)为系统特征方程的系数，其与系统参数、采样时间以及Kpi、Kpv、Kii、Kiv、Kz这5个控制参数相关。因此，引入新的状态变量后，系统阶数和控制参数量是相同的，系统的极点可实现任意配置。取系统期望的主导极点对应的阻尼比为ζλ=0.7，对应的自然谐振频率为ωλ=4 000rad/s，同时令系统的3个非主导极点相等，且都位于实轴上，其距虚轴的距离10 倍于主导极点，则此时系统的5个极点分别为

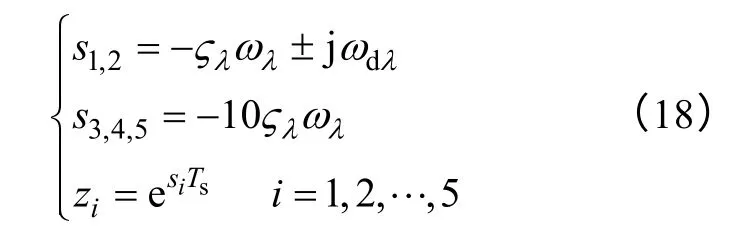
画出系统相应的Bode 图如图6 所示，系统的相位裕度为43°，闭环带宽为1.74kHz 左右，具有较好的稳定裕度和较快的响应速度。图7为系统的根轨迹图和闭环零极点分布图，通过极点配置法将原本处于不稳定和临界稳定的系统极点配置在期望的极点位置上。系统的输出阻抗Bode 图如图8 所示，其在工频处的输出阻抗为阻感性，数值为0.318Ω，可通过负载电流前馈环节消除其对系统输出电压的影响[17]。

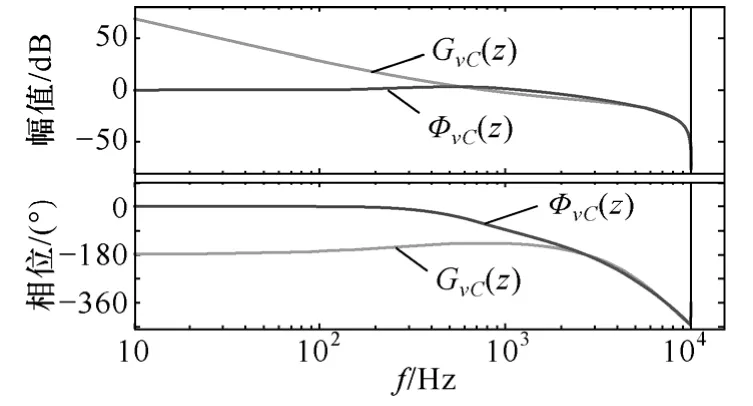
图6 逆变器系统Bode 图Fig.6 Bode diagram of the inverter system

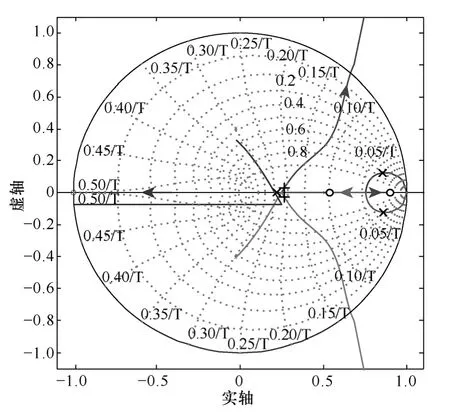
图7 逆变器系统根轨迹图Fig.7 Root locus of the inverter system

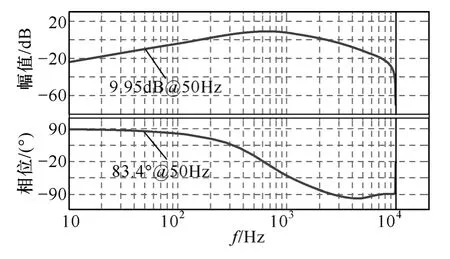
图8 逆变器系统输出阻抗Bode 图Fig.8 Bode diagram of the output impedance of the system

4 仿真与实验分析

4.1 仿真分析

根据表1 所示的参数，运用Matlab 对逆变器进行建模仿真，波形如图9 所示。图9a为系统突加、突减阻性负载时的输出电压波形，满载时THD=1.18%，空载时THD=1.23%，且空载和满载的稳态误差均小于0.2%。图9b为负载突变时A相输出电压和输出电流的仿真波形，其中卸载过程中输出电压超调为8.8%，调节时间小于2ms；突加负载过程中，输出电压的超调约为7.9%，调节时间小于3ms，系统具有较快的动态响应速度。图9c为逆变器带非线性负载（采用电容滤波的三相不控整流接电阻负载）的输出电压和电流波形。此时，由于前馈环节并不能完全消除输出阻抗的影响，输出电压上产生了与输出电流频次相同的低次谐波，其THD=3.09%，满足5%的设计要求。

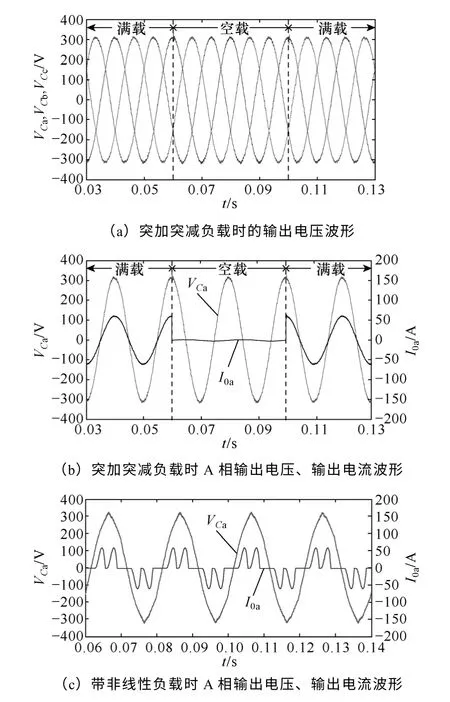
图9 逆变器仿真波形Fig.9 Waveforms of inverter by simulation

4.2 实验结果分析

为了验证本文所提的控制策略，研制了一台实验样机，其参数见表1，控制算法采用DSP（型号为TMS320F2812）实现。实验系统在图4 所示的控制框图基础上增加负载电流前馈，并且增加相应的限幅环节。

图10a～图10c 左图分别为系统空载、满载（带阻感负载，功率因数为0.75）和非线性负载（负载电流峰值达到额定负载电流峰值）时A相的输出电压和输出电流波形，三者的稳态误差分别为0.5V、0.8V 和2.2V；空载和阻感负载时系统具有很好的输出波形；非线性负载时，输出电流峰值约为61A，波峰因子为3.27，此时系统的THD 仍能限制在5%以内，可见系统对非线性负载具有很好的适应能力。图10a～图10c 右图为三种工况下输出电压对应的THD 频谱图，其THD 值分别为1.28%、1.39%和3.25%，三者的主要谐波均为频次较低的奇次谐波。图10d 中，由于空载时系统阻尼减小，谐振峰处的谐波为0.3%左右，但并不影响系统的稳定性；图10e 中，系统带阻感性负载，由于死区引起的低次谐波随功率因数的降低而增大，此时，5、7次谐波的幅值分别为0.85%和0.54%，均大于空载时对应次的谐波；图10f为非线性负载时输出电压的THD 频谱图，由于本系统采用极点配置获得了较高的系统带宽，很好地抑制了由输出电流引入的低次谐波（输出电流的THD 接近90%，主要为5次和7次谐波），此时，输出电压中5次谐波为1.82%、7次谐波为1.71%，系统具有较强的波形控制能力。

图10 逆变器输出电压和电流波形及电压THD 频谱图Fig.10 Output voltage and current waveforms and the corresponding THD spectrogram

图11为系统突加突减负载时的实验波形：图11a 中，突加负载时输出电压超调约为8.2%，经过约2.5ms 的调节过程后恢复正常；图11b为系统突卸负载时的输出波形，由于实验中采用交流断路器切断负载，负载电流下降有所减缓，此时卸载过程中输出电压基本没有超调，调节时间小于2ms。可见，采用本文所述控制策略时，系统具有良好的动态特性。

图11 负载突变时输出电压和输出电流波形Fig.11 Output voltage and current waveforms when load changing

5 结论

（1）分析了离散域下逆变器控制参数量与系统阶数的关系，由于滞后一拍的引入使得逆变器离散域模型增加了一阶，系统控制特性随之变差，并且传统的极点配置法将失效。

（2）通过引入控制器输出量作为新的状态变量，使得逆变器系统在离散域设计时实现了极点的任意配置，此时若系统采用双环控制策略，则控制器可以选择为P、PI、PD 或者PID 控制器。

（3）由于新增状态变量来自控制系统内部，无需额外的传感器和辅助算法，控制策略的实现非常简单方便，且适用于单相和三相逆变器系统。

（4）仿真和实验表明，采用本文所提控制策略，逆变器系统稳定可靠，同时具有良好的动态和静态特性，特别适合于开关频率低且需采用滞后一拍控制的大功率逆变电源系统。

[1]Carrasco J M,Franquelo L G,Bialasiewicz J T,et al.Power-electronic systems for the grid integration of renewable energy sources:a survey[J].IEEE Transactions on Industrial Electronics,2006,53(4):1002-1016.

[2]Vandoorn T L,Meersman B,Degroote L,et al.A control strategy for islanded microgrids with DC-link voltage control[J].IEEE Transactions on Power Delivery,2011,26(2):703-713.

[3]赵彪,于庆广,王立雯,等.用于电池储能系统并网的双向可拓展变流器及其分布式控制策略[J].中国电机工程学报,2011,31(Sup.l):244-251.Zhao Biao,Yu Qingguang,Wang Liwen,et al.Bidirectional extensible converter and its distributed control strategy for battery energy storage gridconnected system[J].Proceedings of the CSEE,2011,31(Sup.l):244-251.

[4]郭卫农,陈坚.基于状态观测器的逆变器数字双环控制技术研究[J].中国电机工程学报,2002,22(9):64-68.Guo Weinong,Chen Jian.Study on digital dual-loop control for inverters based on state-observer[J].Proceedings of the CSEE,2002,22(9):64-68.

[5]Ryan M J,Brumsickle W E,Lorenz R D.Control topology options for single-phase UPS inverters[J].IEEE Transactions on Industry Applications,1997,33(2):493-501.

[6]Ide T,Yokoyama T.A study of deadbeat control for three phase PWM inverter using FPGA based hardware controller[C].IEEE Power Electronics Specialists Conference,2004:50-53.

[7]Mattavelli P.An improved deadbeat control for UPS using disturbance observers[J].IEEE Transactions on Industrial Electronics,2005,52(1):206-212.

[8]Houari A,Renaudineau H,Martin J,et al.Flatness-Based Control of Three-Phase Inverter With Output LC Filter[J].IEEE Transactions on Industrial Electronics,2012,59(7):2890-2897.

[9]熊健,史鹏飞,张凯,等.基于积分环节电压微分反馈的逆变器重复控制策略[J].电工技术学报,2007,22(1):85-90.Xiong Jian,Shi Pengfei,Zhang Kai,et al.Voltagedifferential-feedback with integral control plus repetitive control for PWM inverters[J].Transactions of China Electrotechnical Society,2007,22(1):85-90.

[10]Yokoyama T,Kawamura A.Disturbance observer based fully digital controlled PWM inverter for CVCF operation[J].IEEE Transactions on Power Electronics,1994,9(5):473-480.

[11]刘新民,邹旭东,康勇,等.带状态观测器的逆变器增广状态反馈控制和重复控制[J].电工技术学报.2007,22(1):91-95.Liu Xinmin,Zou Xudong,Kang Yong,et al.An inverter based on state-feedback integral control and repetitive control technology with state-observer[J].Transactions of China Electrotechnical Society,2007,22(1):93-98.

[12]Zhang K,Peng L,Kang Y,et al.State-feedback-withintegral control plus repetitive control for UPS inverters[C].IEEE Applied Power Electronics Conference and Exposition,2005:553-559.

[13]彭力.基于状态空间理论的PWM 逆变电源控制技术研究[D].武汉:华中科技大学,2004.

[14]彭力,张凯,康勇,等.数字控制PWM 逆变器性能分析及改进[J].中国电机工程学报,2006,26(18):65-70.Peng Li,Zhang Kai,Kang Yong,et al.Performance analysis and improvement of digital controlled PWM inverter[J].Proceedings of the CSEE,2006,26(18):64-68.

[15]Mattavelli P,Polo F,Dal Lago F,et al.Analysis of control-delay reduction for the improvement of UPS voltage-loop bandwidth[J].IEEE Transactions on Industrial Electronics,2008,55(8):2903-2911.

[16]Deng H,Oruganti R,Srinivasan D.Adaptive digital control for UPS inverter applications with compensation of time delay[C].IEEE Applied Power Electronics Conference and Exposition,2004:450-455.

[17]孔雪娟.数字控制PWM 逆变电源关键技术研究[D].武汉:华中科技大学,2005.

[18]唐诗颖,彭力,康勇.脉宽调制逆变电源数字双环控制技术研究[J].中国电机工程学报,2009,29(15):55-60.Tang Shiying,Peng Li,Kang Yong.Research on dual-loop digital control technique for pulse width modulation inverters[J].Proceedings of the CSEE,2009,29(15):55-60.