无刷直流电机无位置传感器转子位置辨识策略

李凤祥 徐 浩 袁 野 李天宁

（江苏大学电气信息工程学院 镇江 212013）

1 引言

无刷直流电机因其高效率、长寿命、低噪声及其良好的机械特性等优点，在航空、军事、汽车和办公自动化等行业得到了广泛地应用。传统无刷直流电机控制系统的正常运行，需要位置传感器[1]来确定转子相对位置。但位置传感器增大了电机的体积和成本，维修困难，且传感器的连线较多，容易受外界信号干扰。因此，无刷直流电机无位置传感器控制[2-8]成为当前研究热点之一。由于无刷直流电机的反电动势一般难于直接检测，因此通常采用间接方法得到反电动势过零点[9-14]。文献[9-13]使用端电压法得到反电动势过零点，这种方法虽然结构简单，但是需要重构电机中点，滤波电路的使用也会导致检测到的反电动势过零点信号产生相移，需要额外的硬件或者软件对其进行补偿。文献[14]采用三次谐波检测反电动势的过零点，通过虚构电阻网路中点，得到三次谐波过零点与相反电动势过零点的关系。但实际上由于电阻网路的加入，三次谐波的波形失真。同时，对于实际的无刷直流电机，由于电机设计，漏磁[15,16]的存在，反电动势波形平顶宽度往往小于120°。

针对以上方法的不足，本文提出了提出适用于任意平顶宽度梯形波的线反电动势转子位置辨识策略，以期满足无刷直流电机无位置传感器控制。

2 无位置传感器控制原理

无刷直流电机主电路及等效电路如图1 所示。

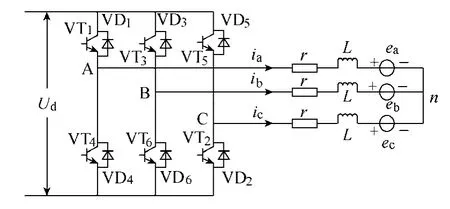
图1 无刷直流电机主电路及等效电路Fig.1 Brushless DC motor main circuit and equivalent circuit

假设无刷直流电机三相绕组对称，忽略齿槽效应和磁路饱和，不计涡流和磁滞损耗，不考虑电枢反应，则无刷直流电机的数学模型

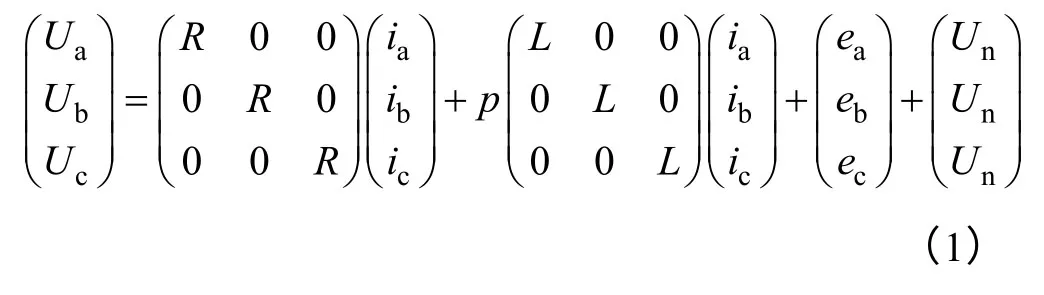
等效为

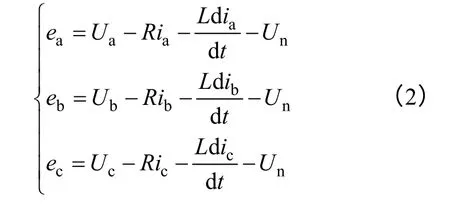
式中，Ua、Ub、Uc分别为三相绕组端电压；R分别为三相绕组等效电阻；ia、ib、ic分别为三相绕组相电流；L为有效电感；p为微分算子；ea、eb、ec为三相绕组的反电动势；Un电机中点电压。

3 传统无位置传感器控制策略

对于反电动势波形为 120°平顶宽度的梯形波的无刷直流电机来说，反电动势、电流与功率器件导通关系如图2 所示。

图2 电机反电动势，电流与功率器件导通关系Fig.2 Relationship between back-EMF,current and on-off of power device

图2 中，G1～G6为三相反电动势过零点，经过30°延迟后，K1～K6为换相时刻，从而实现了功率器件依次换相导通，电机正常运行。但是，该方法只是适用于反电动势波形为平顶宽度为 120°梯形波的无刷直流电机。由于电机的设计制造工艺等问题，反电动势波形往往不是理想的120°平顶宽度梯形波。同时，该方法需要重构有一定误差的电机中性点和导致相反电动势过零点检测延迟的深度滤波电路，限制了无刷直流电机的发展应用。

3 改进的无位置传感器控制策略

3.1 波形定性分析

参照线电压和相电压，现定义三相线反电动势

联立式（2），可得

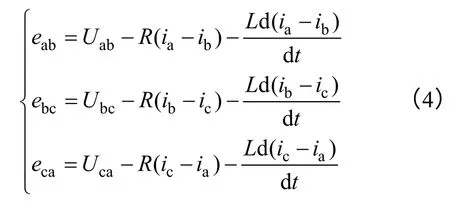
对于反电动势波形为任意平顶宽度梯形波时，假设电机三相对称，则三相梯形反电动势波形相同，且在相位上互差120°。以a 相为例，a 相反电动势波形如图3 所示，反电动势平顶宽度为π-2θ。θ=［π/6，π/2］时，平顶宽度小于120°。

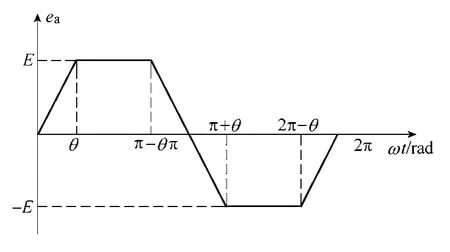
图3 任意平顶宽度的梯形波反电动势波形Fig.3 Arbitrary flat top width trapezoidal waveform of back-EMF

根据图3，得到三相反电动势的表达式

令k1=E/θ，k2=Eπ/(3θ)，代入式（4），得

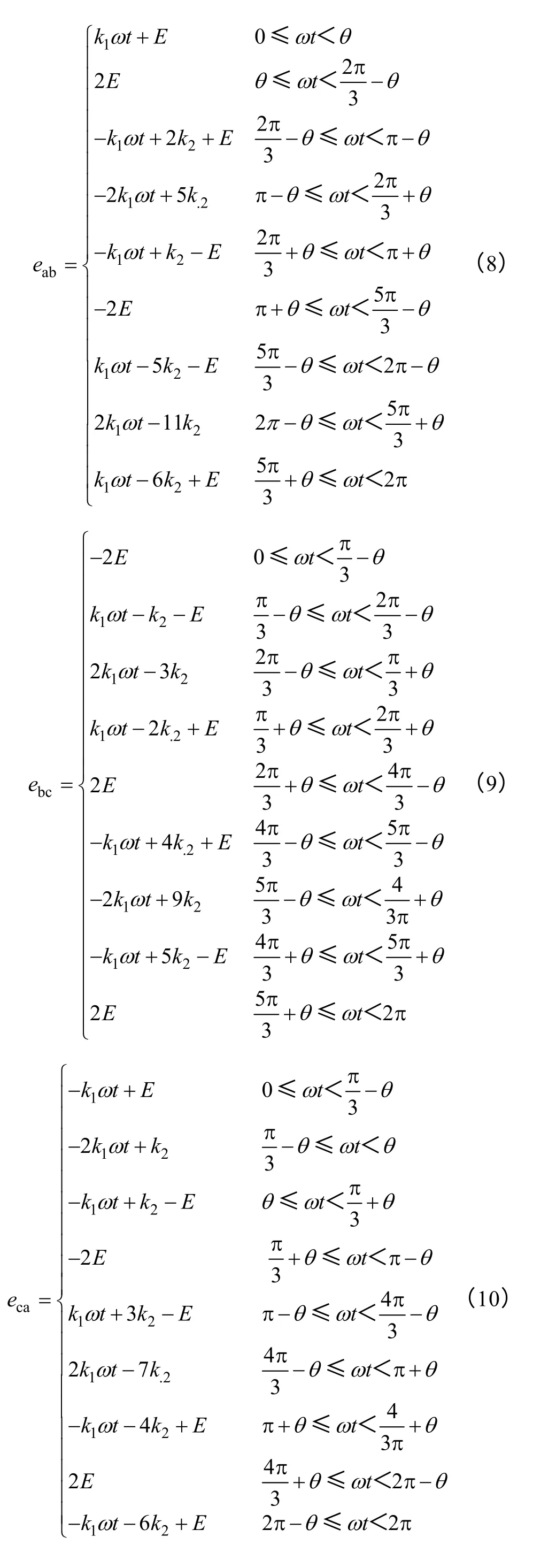
得到相应线电动势波形如图4 所示。

图4 任意平顶宽度相、线反电动势波形Fig.4 Phase and line back-EMF waveforms

对波形进行定性分析，得到结论：eab的两个过零点时刻S3=5π/6、S6=11π/6 为实际的换相点。同理ebc、eca的过零点也是对应相的换相点。

3.2 理论证明

根据图3 可知，相反电动势是周期为的奇函数。根据傅里叶级数展开理论，其傅里叶级数是只含有正弦波的正弦级数

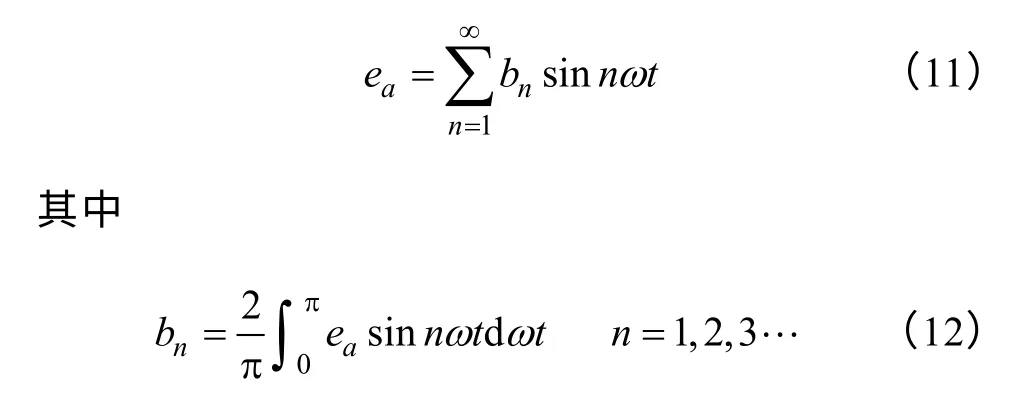
将式（5）代入（12），可以得到

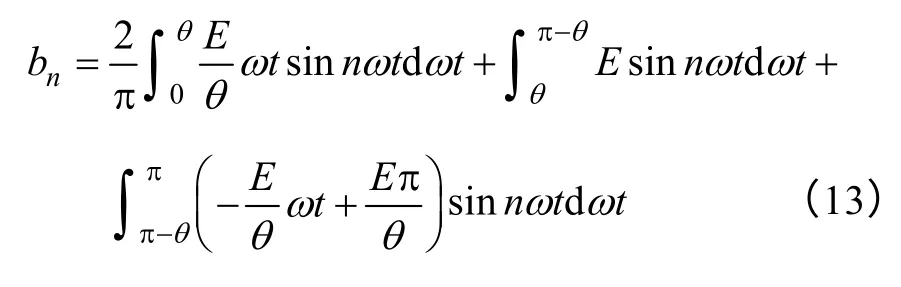
令x=tω，则

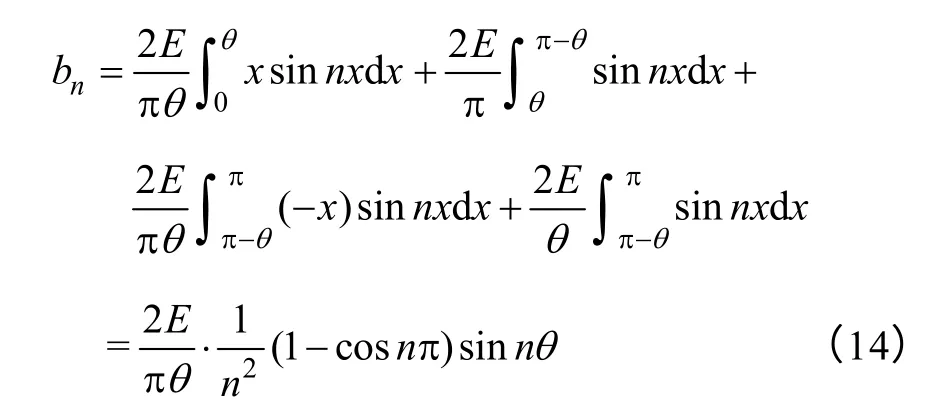
当n为偶数时，bn=0

n奇数时候，

得到相反电动势ea的傅里叶级数表达式

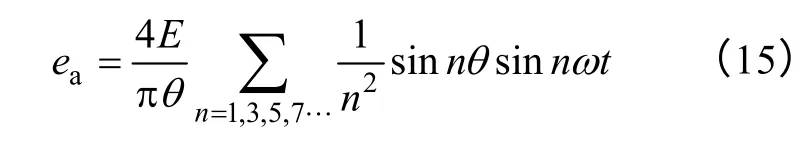
同理，得到b 相的反电动势

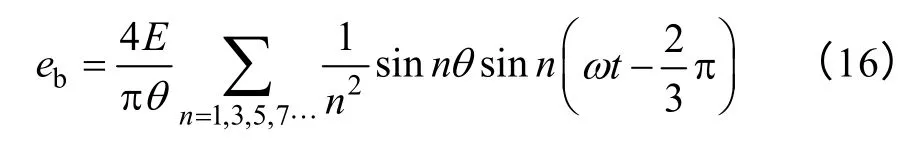
明显，上述表达式只包含了基波、3 次谐波和高频奇次谐波。

结合式（15）与式（16），得到eab傅里叶表达式

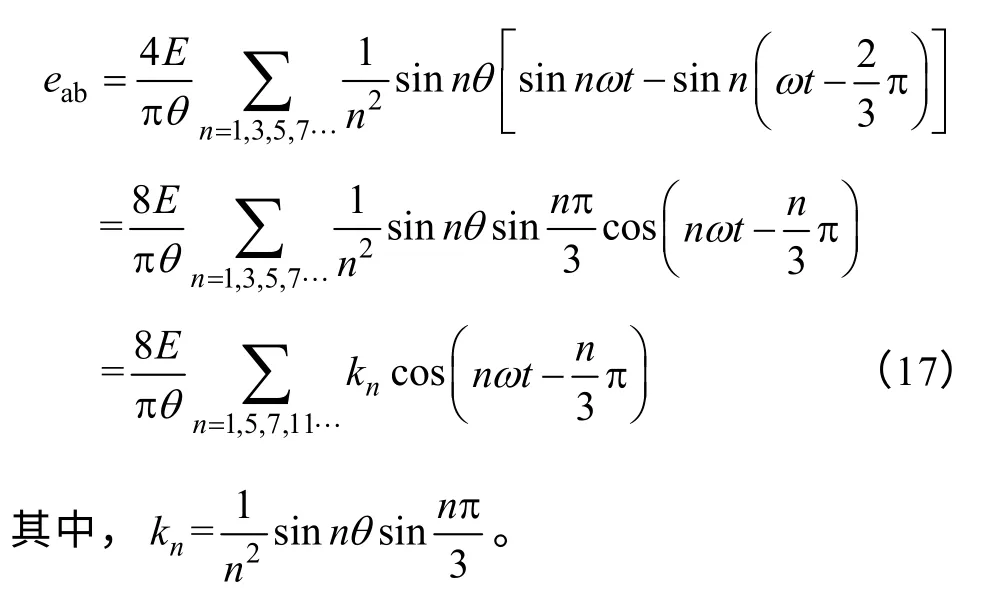
显然，线反电动势中也只含有基波和奇数次谐波成分，不含3n（n=1，2，3…）次谐波。同时，谐波系数kn与n成反比，n越大，kn越小。因此，忽略高次谐波，得到eab的简化表达式为

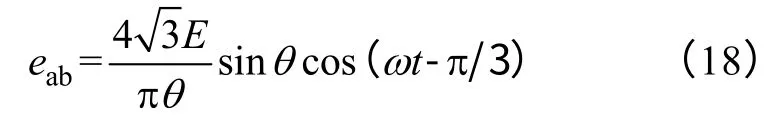
在一个电周期内，eab的过零点为5π/6、11π/6。与波形定性分析得到的结论一致。

从而进一步证明了对于任意平顶宽度梯形相反电动势波形的无刷直流电机，其线反电动势过零点就是实际换相点。

4 实验验证

实验平台采用额定功率为700W，额定电压为60V，额定转速为600r/min 的电动车用轮毂式无刷直流电机搭建，电源采用0～100V 连续可调的直流稳压电源。

4.1 无位置传感器模拟霍尔波形

正确检测转子位置不仅可以保证无刷直流电机的正常换向，而且可以保证产生正确的速度控制量。图5和图6 分别为电机启动与稳态过程中，与电机内部实际安装的转子位置霍尔传感器输出信号与采用无位置传感器检测方案输出的模拟霍尔信号的对比图。由图5和图6 可知，无论电机启动还是稳态过程，无位置传感器检测方案输出的转子位置信号都能准确反映出电机转子的实际位置，与实际物理传感器检测结果一致，实验结果验证了本文检测方案的有效性。

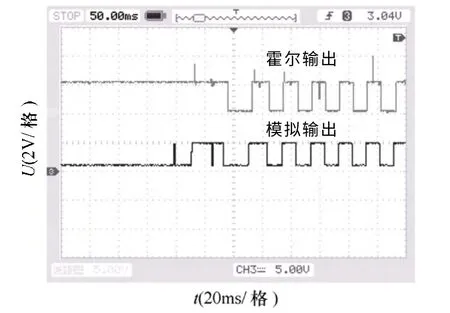
图5 启动过程中霍尔信号与模拟霍尔信号对比Fig.5 Comparison of actual Hall signal and analog Hall signal during the starting process

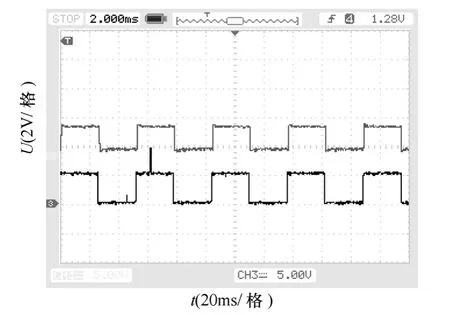
图6 稳态过程中霍尔信号与模拟霍尔信号对比Fig.6 Comparison of actual Hall signal and analog Hall signal during the steady state process

4.2 无位置传感器电机相电流波形

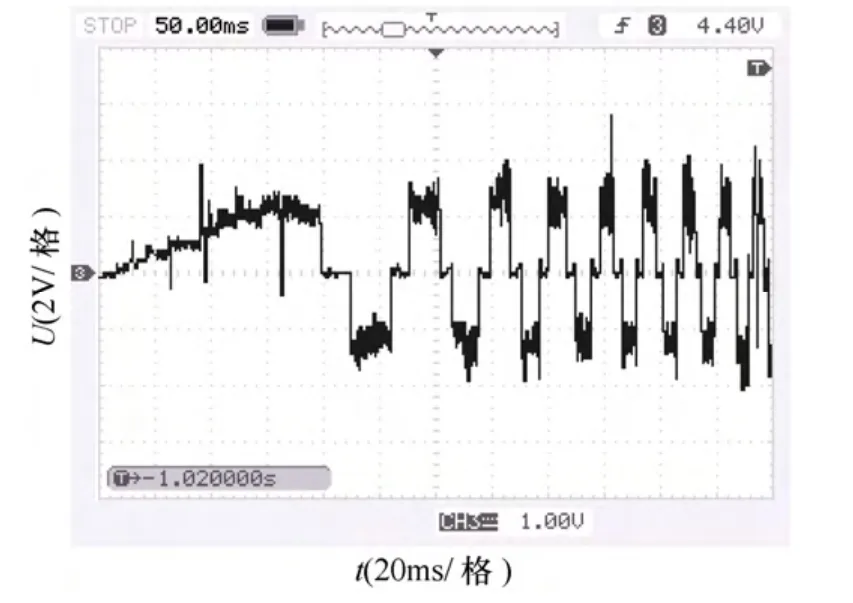
图7 启动过程中的相电流波形Fig.7 Waveforms of phase current during the starting process

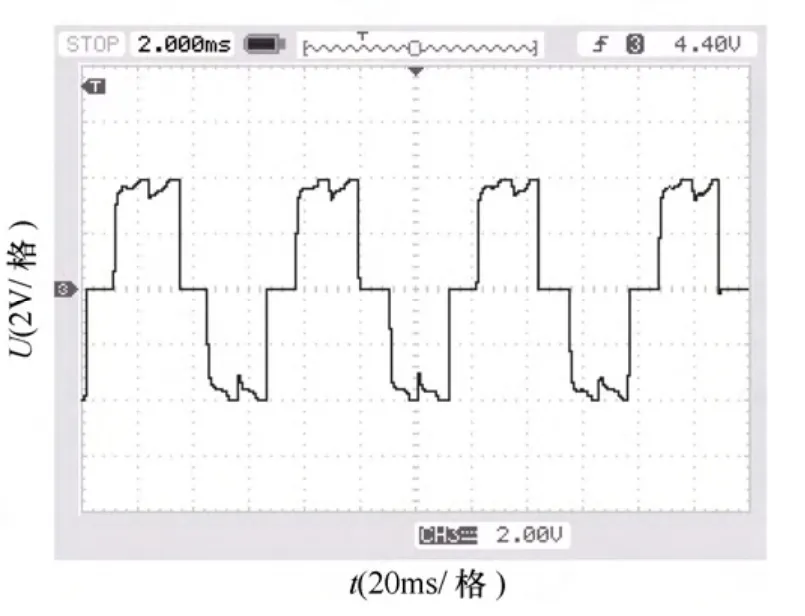
图8 稳态下的相电流波形Fig.8 Waveforms of phase current during steady state process

图7和图8 为启动过程和稳态过程下的电机相电流波形，由于无刷直流电机需要根据转子位置确定电机电流的控制方式，从这两个图可以看出，电机电流波形为方波形状，基本实现了控制目的，这也从另一个方面表明了本文提出的检测方案适用于无刷直流电机的转子位置检测。

5 结论

为了降低传统无位置控制方法的复杂性，提高确定换相时刻的精确度，提出了无刷直流电机无位置传感器任意平顶宽度梯形波转子位置辨识策略，通过线反电动势波形定性分析和傅里叶级数定量推导，证明了对于任意反电动势波形的无刷直流电机，其线反电动势过零点就是换相点，无需重构电机中性点，无需相位补偿电路。实验验证了方法的有效性，具有一定的理论和工程应用价值。

[1]Tae-Hyung Kim,Ehsani M.Sensorless control of the BLDC motors from near-zero to high speed[J].IEEE Transactions on Power Electronics,2004:1635-1645.

[2]谭建成.永磁无刷直流电机技术[M].北京:机械工业出版社,2011.

[3]Liu Y,Zhu Z Q,Howe D.Commutationtorque-ripple minimization in direct-torque-controlled PM brushless DC drives[J].IEEE Transactions on Industry Applications,2005,43(4):1012-1021.

[4]谭博,马瑞卿,刘卫国.一种永磁无刷直流电动舵机四象限控制[J].电工技术学报,2011,26(9):73-79.Tan Bo,Ma Ruiqing,Liu Weiguo.Afour-quadrant control for permanent magnet brushless DC electric actuator[J].Transactions of China Electrotechnical Society,2011,26(9):73-79.

[5]Xia Changliang,Guo Chen,Shi Tingna.A neural network identifier and fuzzy controller based algorithm for dynamic decoupling control of permanent magnet spherical motor[J].IEEE Transactions on Industrial Electronics,2010,57(8):2868-2878.

[6]Xia Changliang,Li Zhiqiang,Shi Tingna.A control strategy for four-switch three-phase brushless DC motor using single current sensor[J].IEEE Transactions on Industrial Electronics,2009,56(6):2058-2066.

[7]Shi Tingna,Guo Yuntao,Song Peng,et al.A new approach of minimizing commutation torque ripple for brushless DC motor based on DC-DC converter[J].IEEE Transactions on Industrial Electronics,2010,57(10):3483-3490.

[8]Qi G,Chen J T,Zhu Z Q,et al.Influence of skew and cross-coupling on flux-weakening performance of permanent-magnet brushless AC machines[J].IEEE Transactions on Magnetics,2009,45(5):2110-2117.

[9]Kim D K,Lee K W,Kwon B I.Commutation torque ripple reduction in a position sensorless brushless DC motor drive[J].IEEE Transactions on Power Electronics,2006,21(6):1762-1768.

[10]Lai Y S,Lin Y K.A unified approach to back-EMF detection for brushless DC motordrives without current and hall sensors[J].IEEE Transactions on Power Electronics,2003,18(6):1293-1298.

[11]Xia Changliang,Song Peng,Li Hongfeng,et al.Research on torque calculation method of permanentmagnet spherical motor based on the finite-element method[J].IEEE Transactions on Magnetics,2009,45(4):2015-2022.

[12]Maurisso V,Luk P C K,Alukaiday T.Sensorless control of a brushless DC motor on the ADMC330 DSP[C].Proceedings of IEE Colloquium on DSP Chips in Real Time Measurement and Control,Leicester,1997:1-5.

[13]Chen C H,Cheng M Y.Implementation of a highly reliable hybrid electric scooter drive[J].IEEE Transactions on Industrial Electronics,2007,54(5):2462-2473.

[14]Wu H X,Cheng S K,Cui S M.A controller of brushless dc motor for electric vehicle[J].IEEE Transactions on Magnetics,2005,41(1):509-513.

[15]李凤祥,袁野.基于动态柔性变结构的控制系统优化设计[J].电子学报,2013,41(5):1025-1029.Li Feng Xiang,Yuan Ye.Optimized design of control system based on dynamic soft variable structure[J].Chinese Journal of Electronics,2013,41(5):1025-1029.

[16]李凤祥,朱伟进.无刷直流电机双模控制技术研究与应用[J].电机与控制学报,2013,17(3) :70-75.Li F X,Zhu W J.Research and application of dualmode operation technology of brushless DC motor[J].ElectricMachines and Control,2013,17(3):70-75.