三相四桥臂逆变器的非数字化控制策略
1 引言
三相四桥臂逆变器由于能够克服不平衡和非线性负载造成的输出电压不对称和畸变问题,在三相逆变器的研究中备受青睐[1-4]。
近年来出现了许多三相四桥臂逆变器的控制策略。文献[5-9]采用了三维空间矢量控制策略,其基本思路是通过坐标变换实现正序、负序和零序分量的独立控制,可以实现逆变器的无静差控制,直流母线电压利用率也较高,是三相四桥臂逆变器研究较多的一种控制方法。文献[10,11]采用了开关点预置的控制策略,其基本思路是利用矩形波傅里叶分解的思想,通过计算开关时刻的角度,控制波形奇对称和正负半周中心对称,从而消除特定的谐波,使逆变器具有输出电压波形失真小的优点。由于三维空间矢量控制策略需要进行坐标变换,而开关点预置控制策略需要计算开关点,因此这两种控制方法的实现都离不开复杂的数学计算,必须依靠数字处理器来实现,属于数字化控制。
虽然数字化控制是变换器控制未来研究的一个方向,但就目前的现状来看它的发展必然会受到客观条件的限制。主要体现在两个方面:①特殊的数字信号处理器很难购买,例如国内很难买到高速的军用级DSP芯片,这就直接导致数字化控制无法在军用和航天等特殊领域应用。②数字化控制的控制效果受处理器运算速度、控制的复杂程度及被控对象频率等因素的影响。在DSP处理速度不高、控制较复杂和被控对象频率较高的情况下,数字化控制就很难实现其预期的控制效果。因此研究三相四桥臂逆变器的非数字化控制具有一定的意义。
非数字化控制可采用滞环和PWM等控制方法。文献[12]采用三态电流滞环控制策略,但由于使用了最大误差电流调节方案,最终还是依靠DSP来实现其控制。文献[13-16]采用PWM控制策略,在电压调制波中加入三次谐波,但这种控制方法实际上属于开环控制,逆变器的动、静态性能不会太高。
本文研究了一种三相四桥臂逆变器的非数字化控制策略,该控制方法控制简单不需要借助复杂的计算,因此可以不依赖DSP,完全通过模拟电路实现,克服了数字化控制目前存在的缺点。同时又由于是闭环控制,逆变器动静态性能也较为优越,且具有良好的带不平衡负载能力。
2 三相四桥臂逆变器数学模型
三相四桥臂逆变器主电路拓扑如图1所示。

图1 三相四桥臂逆变器结构图Fig1 Configuration of three-phase four-leg inverter
假设直流电源为E,电源电流为ii,三相输出滤波电感均为Lf,第四桥臂电感为Ln,电感电流分别为iLa、iLb、iLc和iLn,三相输出滤波电容均为Cf,三相负载为Ra、Rb、Rc,三相输出电压分别为uoa、uob和uoc。
三相四桥臂逆变器有S1~S8八个开关器件,可用Sa、Sb、Sc、Sn表示每个桥臂的开关函数。当桥臂上管开通,下管关断时,定义此桥臂的开关方式为=1(i=a,b,c,n);当桥臂上管关断,下管开通时,定义此桥臂的开关方式为Si=0(i=a,b,c,n)。令=Sa-Sn,=Sb-Sn, Scn=Sc-Sn,则桥臂输出电压(A,B,C三点相对于N点的电压)与直流侧电源电压之间的关系为

根据以上定义对图1列写电压和电流方程可得

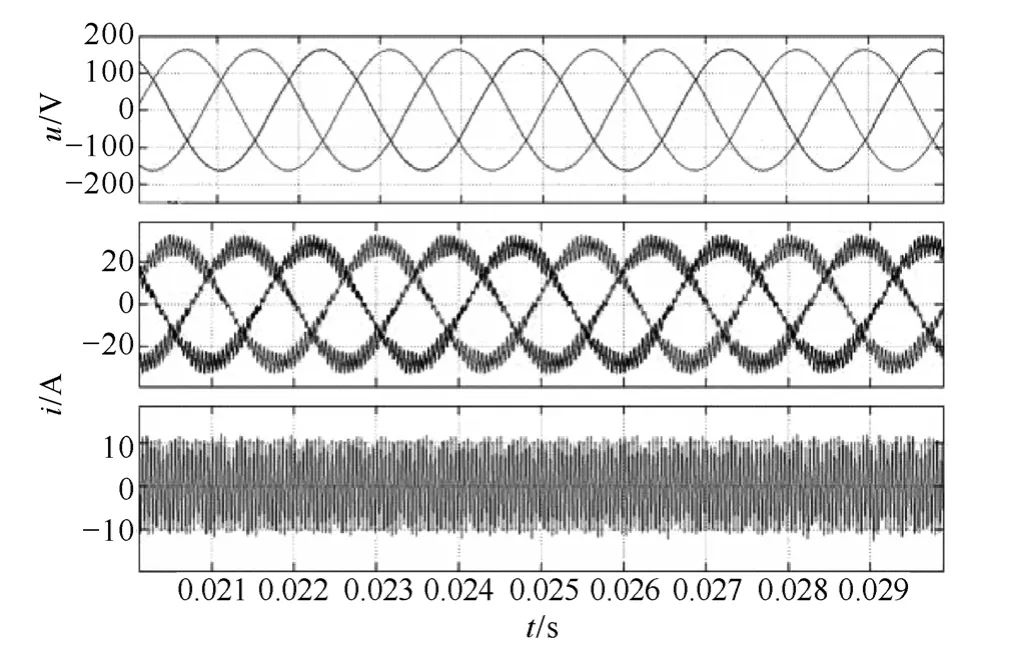
为了减小三相之间的耦合以及 Ln对三相输出电压的影响,通常的做法是:①减小Ln的数值,使得Ln< 由于式(2)、式(6)中开关函数San、Sbn和 Scn为不连续函数,可采用开关周期平均法进行分析,于是可以得到 定义各相桥臂和第四桥臂的合成占空比矩阵为d,则很显然有下面的关系 将式(11)代入式(7)、式(8)和式(10),得到三相四桥臂逆变器的开关周期平均模型数学表达式 由上面三表达式可以得到三相四桥臂逆变器的开关周期平均模型等效电路如图2所示。由此可以看出,三相四桥臂电路的每一相都是独立的,相互之间不存在耦合关系,可以把三相四桥臂逆变器分解成三个独立的单相全桥逆变器进行控制。 图2 三相四桥臂逆变器开关周期平均模型Fig.2 Average switching period model of three-phasefour-leg inverter 根据上文的分析,虽然三相四桥臂逆变器可等效为三个相位互差120°的单相逆变器,但其控制与单相逆变器并不相同,因为每个等效的单相逆变器两个桥臂所采用的控制方法并不相同。因此可以将三相四桥臂逆变器的控制分为两个部分:a、b、c三相桥臂的控制和第四桥臂的控制。很显然只有当各相桥臂和第四桥臂的控制互相配合,才能使逆变器获得良好的控制效果。 本文研究的三相四桥臂逆变器相桥臂的控制方法如图3所示,图3中只给出了a相桥臂的控制原理,由于b、c相的控制方法跟a相相同,只是相位差120°,因此可以a相为例进行说明。 图3 相桥臂控制框图Fig.3 Control block diagram of phase leg 为了使三相四桥臂逆变器能具有较好的动静态特性且易于非数字化实现,a、b、c三相采用了改进的电压电流瞬时值反馈控制。输出电压uoa经电压反馈电路得到uaf,uaf和电压给定信号uar比较后经过PI控制器和谐振控制器,得到电流给定信号iar,之所以在PI控制器后加谐振控制器,是因为电压环如采用传统的PI控制并不能实现逆变器的无静差控制,将谐振控制器引入电压环,利用内模控制原理可实现了逆变器输出电压的无静差,其效果相当于空间矢量控制方法里在dq坐标系下的PI控制。而保留PI控制器可在不改变原控制参数的基础上,突出加入谐振控制器取得的优化效果。电感电流iLa经电流反馈电路得到iaf,iaf与电流给定信号iar比较后,经过电流控制器生成调制波信号uat,这里电流控制器采用P控制或PI控制皆可。最后给uat补偿零序谐波u0r后,与三角载波信号交截产生a相桥臂上下两个管子的开关信号。很显然在调制过程中由于补偿了零序谐波电压,降低了相零序电流对相电压产生的畸变影响,使得三相输出电压更接近正弦波。另外零序谐波补偿有利于降低调制波的峰值,相当于提高调制比,因此采用该控制方法的三相四桥臂逆变器比三相半桥逆变器直流母线电压利用率可以提高约15%。由于本控制方法将零序谐波补偿到双闭环之后,因此适合用于电压电流双闭环控制方法中,而双闭环控制较开环的PWM控制具有更好的动静态性能,克服了文献[13-16]的缺点。 那么如何得到补偿的零序谐波电压呢?本文通过将 a、b、c三相电压调制信号 uat、ubt和uct分别经正、负半波整流电路整流后相加。由于m脉波整流电压经傅里叶分解可得到直流分量和谐波次数为mk次(k=1,2,3…)的谐波分量,很显然三相电压调制信号分别经正、负半波整流电路整流后相加直流分量可抵消为零,而剩下的只有3k次谐波,从而得到所需的零序谐波分量u0r。 第四桥臂的控制只能对零序电压分量进行控制[6]。将得到的零序谐波电压u0r作为第四桥臂的调制信号,跟三角载波交截后,即可产生第四桥臂上、下两管的控制信号,第四桥臂控制原理框图如图4所示。 于是逆变器8个开关器件的控制信号都能得到,从而实现了三相四桥臂逆变器的控制。 图4 第四桥臂控制框图Fig.4 Control block diagram of the fourth leg 由图3逆变器的相桥臂控制框图和图4逆变器的第四桥臂控制框图可以看到,图中的电压、电流反馈电路、PI控制器、P控制器、三相调制电压的正负半波整流电路以及载波交截电路都很容易通过模拟电路实现,只有谐振控制器较难实现。因此本控制策略的硬件实现的关键在于谐振控制器的模拟电路实现。 谐振控制器的传递函数为 式中,ω为谐振角频率;A0为谐振频率ω处的放大倍数,主要决定谐振控制器的增益;Q为品质因数,主要决定谐振控制器的带宽。 图5为谐振控制器的伯德图,由其幅频特性曲线可以看出,该谐振控制器在谐振点400Hz处,控制器增益最大,如果频率偏离谐振点,控制器增益逐渐减小,最终增益变为零,即幅值增益有一定带宽。这一特性使该控制器可以克服器件参数变化或逆变器频率变化带来的谐振点偏差,进而造成的控制效果变差的不利因素。也就是说,如果逆变器的输出频率和谐振控制器的谐振频率存在误差,那么只需要通过合理设计谐振控制器的增益A0和品质因数Q,保证在逆变器的输出频率处,谐振控制器能产生足够大的增益,就能实现谐振控制。概括起来谐振控制器的参数设计原则主要为两点:①根据逆变器的性能指标选择适当的A0。②根据控制元器件的精度选择Q。 图5 谐振控制器伯德图Fig.5 The Bode chart of resonant controller 实际上可认为式(15)给出的谐振控制器是一带通滤波器。从这一思路出发,不难构建图6的模拟电路。图中运放A1、电阻R1~R4和电容C1~C2构成二阶带通有源滤波器,主要完成谐振控制器放大倍数和带宽等参数的设置,是谐振控制器的核心电路。其传递函数为 图6 谐振控制器的模拟电路Fig.6 Analog circuit of resonant controller 运放A2和电阻R5~R7实现反向的比例环节,其传递函数为 运放A3、电阻R8~R11构成反向加法器,实现比例环节和二阶带通有源滤波器的组合,其传递函数为 于是可以得到整个模拟电路的传递函数为 对比式(15)和式(19)可以看到,只需合理选择 C1、C2和 R1~R10的值,令其满足式(20)的关系,即可用该模拟电路来实现谐振控制器的控制。 为了验证上述方案的可行性,本文设计了一台原理样机,进行了仿真和实验验证。样机参数如下:直流母线电压290V,交流输出电压有效值115V,输出电压频率400Hz,三相额定负载6kV·A,每相2kV·A,输出滤波电感每相240μH,输出滤波电容每相 14μH。 图7和图8分别给出了逆变器在三相平衡阻性额定负载情况下的仿真和实验波形。图7中给出了三相电压波形、三相电感电流波形和中线电感电流波形。 图7 平衡负载仿真波形Fig.7 Simulation waveforms of balance loads 图8 平衡负载实验波形Fig.8 Experimental waveforms of balance loads 图8中波形为a相电感电流波形和三相输出电压波形。从仿真和实验都可以看到输出电压波形正弦度较高,畸变很小,因此该控制方法可以有效的实现三相四桥臂逆变器的控制。 图9给出了逆变器引入谐振控制器和不引入谐振控制器两种方案下的外特性实验对比曲线。可以看到加入谐振控制器后,逆变器输出电压基本不变,外特性非常硬。 图9 逆变器外特性曲线Fig.9 External characteristic of inverter 下表给出了逆变器带三相不对称负载情况下的实验数据。 表 不对称负载下的实验数据Tab. Data of unbalanced loads 图10为2/3不平衡负载条件下的三相电感电流波形和中线电流波形。 上表和图10的实验结果表明,采用本文研究的控制策略的三相四桥臂逆变器当负载功率出现不平衡时,输出电压仍能保持平衡,因此该逆变器具有较强的带不平衡负载能力。 图10 不平衡负载实验波形Fig.10 Experimental waveforms of unbalanced loads 图11给出逆变器a相突加额定负载的动态实验波形,图中波形分别为a相电感电流波形和三相输出电压波形,可以看出当电流突然发生变化时,三相输出电压在突变时刻产生畸变,但仅用了约200μs输出电压就恢复了正常,这说明逆变器具有较好的动态性能。 图11 动态实验波形Fig.11 Dynamic experimental waveforms 本文通过构建了三相四桥臂逆变器的开关周期平均模型,将三相四桥臂逆变器等效为三个单相逆变器来控制。每个单相逆变器由相桥臂和第四桥臂组成。相桥臂采用加入谐振控制器和补偿零序谐波的改进型电压电流双闭环控制策略,第四桥臂采用零序谐波电压PWM控制。该控制策略不但使逆变器具有输出波形质量好、动静态性能良好等优点,还具有简单易于实现,可不借助数字处理器,仅用模拟电路就可实现其控制的特点。克服了数字化控制目前存在的一些缺点,使得三相四桥臂逆变器具有更广泛的应用前景,有较好的工程应用价值。 [1] 孙驰,马伟明,鲁军勇.三相逆变器输出电压不平衡的产生机理分析及其矫正[J].中国电机工程学报,2006,26(21):57-64.Sun Chi, Lu Junyong, Ma Weiming. A novel controlmethod for three-phase four-leg inverter[J]. Transactionsof China Electrotechnical Society, 2007, 22(2):57-63. [2] 孙驰,鲁军勇,马伟明.一种新的三相四桥臂逆变器控制方法[J].电工技术学报,2007,22(2):57-63.Sun Chi, Lu Junyong, Ma Weiming. A novel controlmethod for three-phase four-leg inverter[J]. Transactionsof China Electrotechnical Society, 2007, 22(2):57-63. [3] 孙驰,毕增军,魏光辉.一种新颖的三相四桥臂逆变器解耦控制的建模与仿真[J].中国电机工程学报,2004,24(1):124-130.Sun Chi, Bi Zengjun, Wei Guanghui. Modeling andsimulation of a three-phase four-leg inverter based ona novel decoupled control technique[J]. Preceedingsof the CSEE, 2004, 24(1): 124-130. [4] 陈凯.6kV·A三相四桥臂逆变器的研究[D].南京:南京航空航天大学,2011. [5] Zhang Richard, Pasad V H, Dushan Boroyevich.Three-dimensional space vector modulation for fourlegvoltage source converter[J]. IEEE Transactions onPower Electronics, 2002, 17(3): 314-320. [6] Michael J Ryan, Rik W De Doncker, Robert D Lorenz.Decoupled control of a four-leg inverter via a new4×4 transformation matrix[J]. IEEE Transactions onPower Electronics, 2001, 16(5): 694-701. [7] Olorunfemi Ojo, Parag M Kshirsagar. Concise modulationstrategies for four-leg voltage source inverter[J].IEEE Transactions on Power Electronics, 2004, 19(1):46-53. [8] Dhaval C Patel, Rajendra R Sawant, Mukul Cchandorkar. three-dimensional flux vector modulationof four-leg sine-wave output inverters[J]. IEEE Transactionson Industrial Electronics, 2010, 57(4): 1261-1269. [9] 龚春英,熊宇,郦鸣,等.四桥臂三相逆变器电源的三维空间矢量控制技术研究[J].电工技术学报,2004,19(12):29-36.Gong Chunying, Xiong Yu, Li Ming, et al. Study ofspace vector modulation of four-legged three-phaseinverter[J]. Transactions of China ElectrotechnicalSociety, 2004, 19(12): 29-36. [10]王慧贞,丁勇,张方华,等.开关点预置的四桥臂三相逆变器[J].中国电机工程学报,2008,28(3):73-76.Wang Huizhen, Ding Yong, Zhang Fanghua, et al.Four-leg three-phase inverter based on switchingnodepreset[J]. Preceedings of the CSEE, 2008, 28(3):73-76. [11]张方华,丁勇,王慧贞,等.四桥臂三相逆变器的特定谐波消除控制[J].中国电机工程学报,2007,27(7):83-87.Zhang Fanghua, Ding Yong, Wang Huizhen, et al.The SHE control strategy on three-phase four-leginverter[J]. Preceedings of the CSEE, 2007, 27(7):83-87. [12]阮新波,严仰光.四桥臂三相逆变器的控制策略[J].电工技术学报,2000,15(1):61-64.Ruan Xinbo, Yan Yangguang. The control strategy forthree-phase inverter with four bridge legs[J]. Transactionsof China Electrotechnical Society, 2000, 15(1):61-64. [13]Kim Jang Hwan, Sul Seung Ki. A carrier based PWMmethod for three phase four-leg voltage source converter[J]. IEEE Transactions on Power Electronics, 2004,19(1): 66-75. [14]万山明,吴芳,黄声华.三相四桥臂电压源高频链逆变器[J].中国电机工程学报,2005,25(12):47-51.Wan Shanming, Wu Fang, Huang Shenghua. Threephase four-leg voltage source high frequency linkinverter[J]. Preceedings of the CSEE, 2005, 25(12):47-51. [15]刘秀翀,张化光,陈宏志.四桥臂逆变器中第四桥臂的控制策略[J].中国电机工程学报,2007,27(33):87-92.Liu Xiuchong, Zhang Huaguang, Chen Hongzhi.Control strategy of the fourth leg in four-leg inverter[J]. Preceedings of the CSEE, 2007, 27(33): 87-92. [16]陈宏志,刘秀翀.四桥臂三相逆变器的解耦控制[J].中国电机工程学报,2007,27(19):74-79.Chen Hongzhi, Liu Xiuchong. Decoupling control ofthree-phase four-legged inverter[J]. Preceedings ofthe CSEE, 2007, 27(19): 74-79.



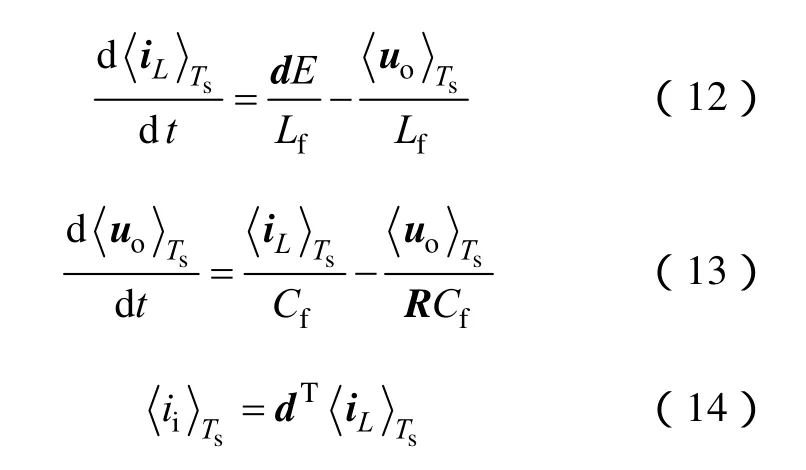

3 逆变器非数字化控制策略


4 非数字化控制硬件实现








5 仿真与实验验证





6 结论

