一次北印度洋海啸的数值模拟研究

陈飞，张芳苒，薛彦广，白志鹏，王颖

（中国人民解放军61741部队,北京 100094）

1 引言

海底的地震和火山喷发，可能引起海水中形成巨大的海浪，并向外传播，这就是海啸[1-2]。海啸的英文“Tsunami”来自日文，是港湾中的波的意思。大部分的海啸都产生于深海地震。深海发生地震时，海底发生激烈的上下方向的位移，某些部位出现猛然的上升或者下沉，产生了其上方的海水巨大的波动，海啸于是就产生了。海啸与一般的海浪不一样，海浪一般在海面附近起伏，涉及的深度不大，而深海地震引起的海啸则是从深海海底到海面的整个水体的波动，其中包含的能量惊人。地震几分钟后，原生的海啸分裂成为两个波，一个向深海传播，一个向附近的海岸传播。向海岸传播的海啸，受到岸边的海底地形等影响，在岸边与海底发生相互作用，速度减慢，波长变小，振幅变的很大(可达几十米)，在岸边造成很大的破坏。海啸是一种海洋表面重力波，波长数十至数百千米，周期2—40 min(比潮汐波周期短，比风浪周期长)，在大洋中传播速度高达每小时720—900 km。海啸波在水域传播时，受水深变化的影响，其传播方向、大小以及剖面形状都要随传播距离而变化。当水深沿波向线逐渐变浅，波能传播速度逐渐减慢，使从后面输入能量的速率大于前面把能量传走的速率，引起波能沿程累积，使波幅逐渐增大。这一现象称为波浪的浅水效应(shoaling)。海啸在大洋中传播能量损失很小，浪高几十厘米到一米左右，不易觉察，到岸时由于浅水作用浪高攀升至数米至数十米，有的可向岸上推进300多米，常常带来巨大破坏。

当前，海啸数值模拟已经成为海啸研究的主要方向[3-5]，各国都建立了自己的海啸研究模型。COMCOT[6]是美国Cornel大学开发的一个成熟的长波模拟数值模式。该模式采用浅水差分方程组模拟海啸传播过程，有线性和非线性两种形式，分别应用于深海和浅海不同的情况。

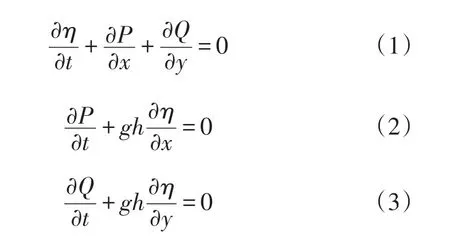
线形浅水方程组的具体表达式如式（1—3）所示，式中的η表示海洋自由表面的扰动，P与Q分别表示x和y方向上按深度平均的体积通量，g为重力加速度，h表示静止状态下的水深。在近海地区水深变浅，非线性对流项增大，科氏力项很小可忽略不计，海底摩擦增大，因此近海海啸采用非线性浅水方程加上底摩擦项，在直角坐标系表示为式（4—6）中的η表示海洋自由表面的扰动，P与Q分别表示x和y方向上按深度平均的体积通量，g为重力加速度，h表示静止状态下的水深，H表示总水深，τx和τy分别表示x和y方向上的海底摩擦项，n是宁曼粗糙系数。海底摩擦影响着爬高过程和浅水区传播过程的水动力特性。

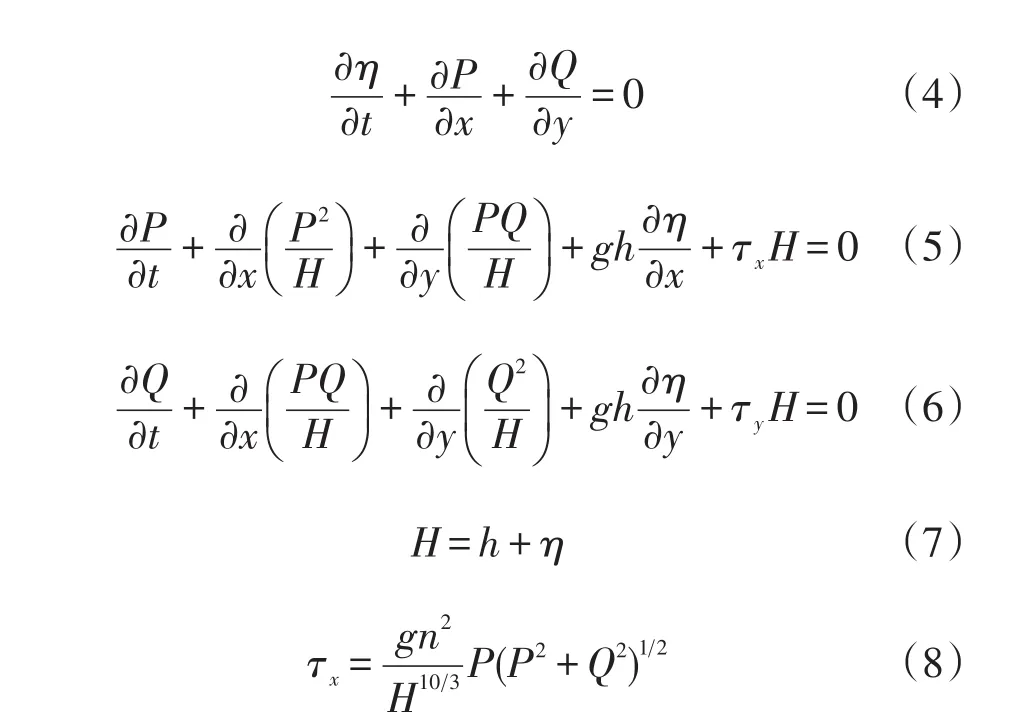
对于地震海啸的模拟，COMCOT模式的初始条件采用基于弹性错移理论的Okada断层模型[7]生成。Okada模型已经包含在COMCOT模式当中。该断层模型一共需要输入9个参数，分别是：震中纬度、震中经度、震源深度、破裂面长度、破裂面宽度，平均滑移量、走向角、倾角和滑移角。有了这些地震参数，我们就可以生成COMCOT模式的初始场。

2 北印度洋海啸过程模拟分析

2.1 海啸波监测及地震参数的获取

世界时2012年4月11日08时39分，在北印度洋印尼苏门答腊北部近海发生了8.6级（M）海底地震。地震引发了海啸，印度洋周边多个国家监测到了海啸波（见图1）。图1中01—12所标注的圆点表示各个测站所在的位置，图中还标注了引发海啸的海底地震震中所在的位置。表1给出了通过气象报报文收集到的12个测站测得的海啸波的波幅等参数。

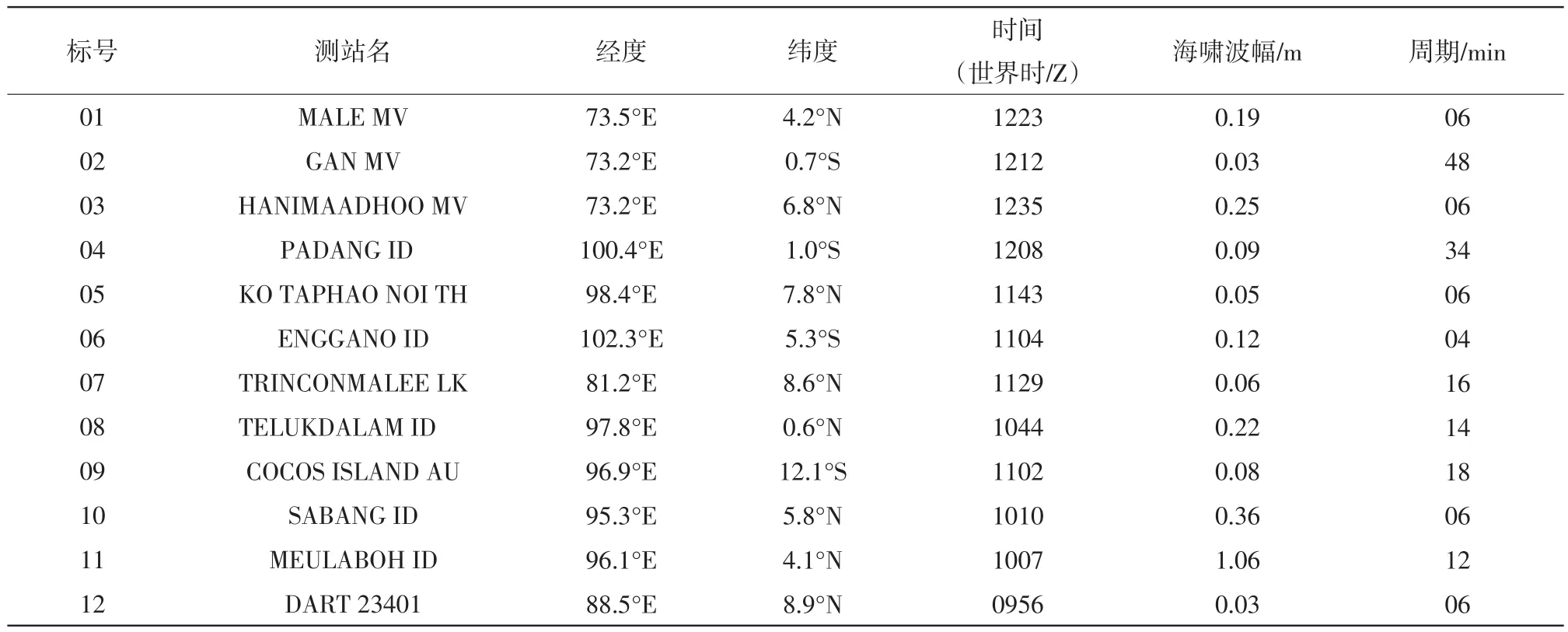
表1 各测站测得的海啸波参数

COMCOT模式的启动需要一个初始场，通过Okada断层模型生成初始场需要以下九个地震参数[8]：

震中纬度、震中经度、震源深度、破裂面长度、破裂面宽度、平均滑移量、走向角、倾角、滑移角。

上述参数的获取可以参考Harvard CMT地震目录，下面列出了其中关于此次北印度洋海底地震的地震参数：

矩震级： Mw=8.6

震中纬度：Lat=2.35N

震中经度：Lon=92.82E

震源深度：Depth=45.6km

走向角: Strike=20°

倾 角: Dip=76°

图1 印度洋海啸模拟区域图（单位/m）

图2 基于弹性错移理论的Okada断层模型计算得到的海啸波的初始场（单位/m）

滑移角: Slip=5°

Harvard CMT地震目录中没有给出关于破裂面长度、破裂面宽度、平均滑移量三个参数的具体值，这三个参数的获取有两种方式。

一种是根据Wells和Coppersmith[9]给出的关于矩震级Mw、破裂面长度L、破裂面宽度W的经验式（10—13）得到。式中L为破裂面长度，W为破裂面宽度，D为平均滑移量，a、b分别为参考系数，μ为介质的刚性系数，一般取值3×1010N m2—5×1010N m2之间，M0为地震矩，Δσ为应力降，位于10—100之间，一般取Δσ=50。如此即可根据矩震级Mw得到破裂面长度L、破裂面宽度W和平均滑移量D的值。

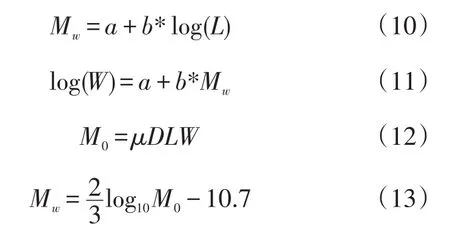
另一种是根据Geller scaling law[10]计算破裂面的长宽及平均滑移量，Geller根据历史地震资料选择 L=2W ，推导出经验式（14），结合式（12），即可得到破裂面长度L、破裂面宽度W和平均滑移量D的值。

我们采用第二种方法，取 μ=3.5×1010，Δσ=50，得到地震参数：

破裂面长度：L=230.792 km

破裂面宽度：W=115.396 km

平均滑移量：D=9.5614 m

2.2 海啸过程模拟分析

得到了相关的地震参数，我们就可以对这次海啸过程进行模拟。模拟需要的水深数据选用ETO⁃PO1.dat数据，模拟区域为（20.0°S—25.0°N ，60°E—110°E），见图1。由于模式运算中使用的地形分辨率为4'×4'，这里我们通过对ETOPO1.dat数据进行双线性差值得到。考虑到模拟区域较大，我们所关心的是海啸波的越洋传播过程，水深较大，所以应该采用线性球坐标系，不计底摩擦的影响。通过基于弹性错移理论的Okada断层模型计算得到的海啸波的初始场见图2。

根据Okada断层模型计算得到的海啸波的初始场，进行了28800 s（8 h）时间长的模拟。为了验证模拟结果的准确性，分别选择了03、09、12三个站点（见图1），对这三个位置上海啸波幅随时间的变化进行了模拟。其中03号测站在海啸发生236 min后测得0.25 m的海啸波；09号测站在海啸发生143 min后测得0.08 m的海啸波；12号测站在海啸发生77 min后测得0.03 m的海啸波。图3分别为模式计算得到的三个位置上的海啸波幅图，从图中可以看出模式模拟的海啸波的传播时间和波幅与实际观测值基本上相吻合，模式模拟结果能够反映出海啸波的真实传播过程。

图3 模拟的海啸波高曲线图

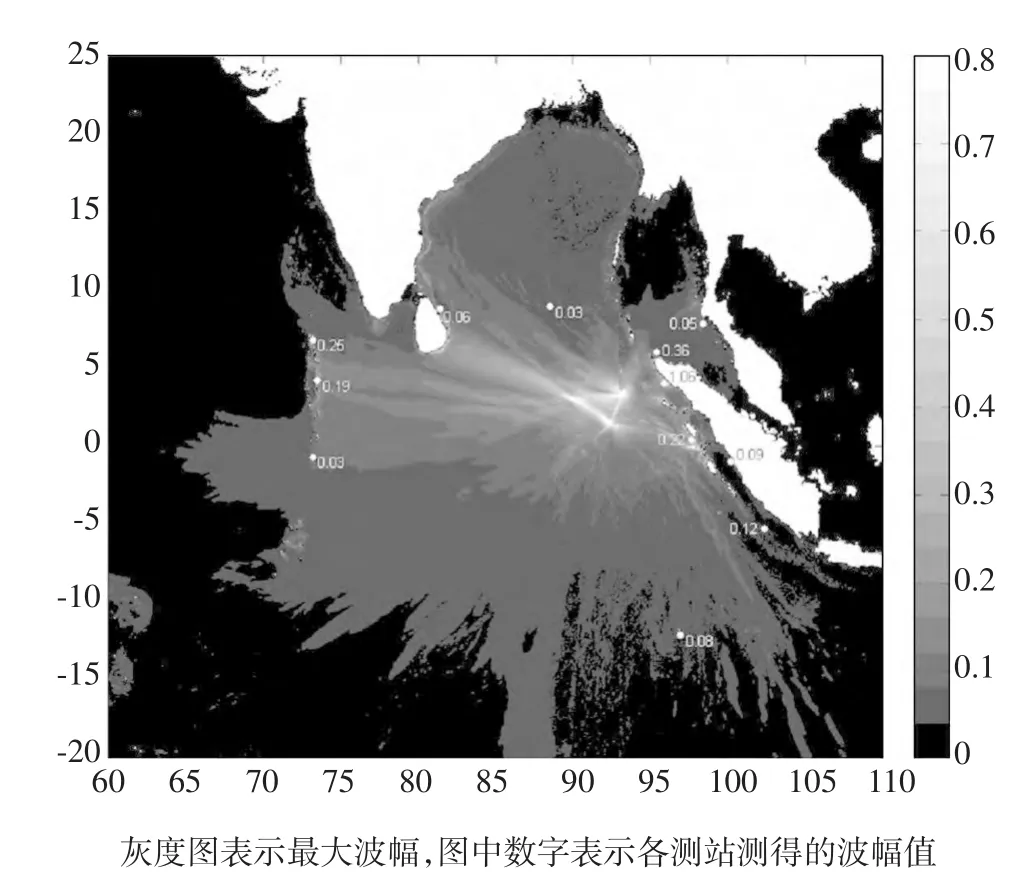
图4 海啸波传播最大波幅分布图（单位/m）

图4为模拟的海啸波传播最大波幅分布图。图中给出了海啸发生后传播8 h的最大波幅分布情况，灰度图表示模拟区域各点的最大波幅值，颜色越亮，波幅越大。从图中可见，此次海啸能量的主体向东、西两个方向传播，01、03号测站位于西部马尔代夫群岛沿海一带，海啸波到达该地区需要传播大约3h 40 min（见表1），但是监测到的波幅相对要大一个量级，因此该方向上能量要比其它方向大的多，这也说明了该方向上能量主体的存在。东部苏门答腊岛沿海距离震源中心较近，影响也较大，由08、10、11号测站实况可知，海啸波到达该区域，只需要1—2 h，该区域也是此次海啸最先影响的区域。

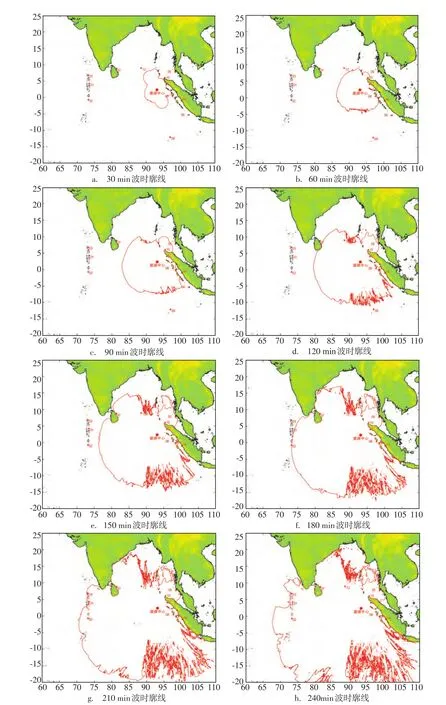
图5 海啸波0.03 m波幅传播波时图，时间间隔30 min

图5给出了海啸波0.03 m波幅传播波时图，从海啸发生起，传播4 h，每间隔30 min绘制一次。海啸波最先影响苏门答腊岛北部沿海；由于能量主要集中在东西两个方向上，南北方向能量传播较少，因而南北向波幅较小，而且能量随着时间逐渐衰减，当海啸波传播到120 min时，受到网格分辨率的限制，南北方向已经无法得到完整的海啸波时廓线。在能量较集中的偏西方向上，当前分辨率能够描绘出完整的波时廓线。由于图5给出的是0.03 m海啸波幅的波时廓线，各测站测量的时间是测站所在位置的最大波时间，因而这两者是不一致的，但是我们可以根据测站实况定性判断海啸波时廓线的走向。

3 结论

本文对世界时2012年4月11日发生在北印度洋的一次地震海啸进行了模拟分析。给出了海啸波监测数据和地震参数的获取途径，以及海啸波初始场的构造方法。根据模拟结果绘制了海啸波传播最大波幅分布图，此次海啸的能量主体是沿东西两个方向传播。文章还绘制了海啸波传播波时图，并对单点测站的海啸波高曲线进行了模拟，与测站实况进行对比可知，模式模拟的海啸波传播过程是合理的。分析可见，海啸波的能量传播方向是不均匀的，在能量传播集中的方向，波幅较大，造成的危害也较大。

[1]包澄澜.海啸及风暴潮灾害简介[J].东北地震研究,2005,21(2):9-15.

[2]魏柏林,何宏林,郭良田,等.试论地震海啸的成因[J].地震地质,2010,32(1):150-161.

[3]祝会兵,于颖,戴世强.海啸数值计算研究进展[J].水动力学研究与进展A卷，2006,21(6):714-723.

[4]温燕玲,朱元清.海啸传播模型与数值模拟研究进展[J].地震地磁观测与研究,2007,28(5):143-150.

[5]姚远,蔡树群,王盛安.海啸波数值模拟的研究现状[J].海洋科学进展,2007,25(4):487-494.

[6]潘文亮,王盛安.COMCOT数值模式的介绍和应用[J].海洋预报,2009,26(3):45-52.

[7]Okada M.Surface deformation due to shear and tensile faults in a half-space[J].Bull Seism SocAm,1985.75(4):1135-1154.

[8]Mansinha.The displacement fields of inclined faults[J].Bull Seism SocAm,1985,61:1433-1440.

[9]Liu P L F,Wang X M,Salisbury A J.Tsunami hazard and early warning system in South China Sea[J].Journal of Asian Earth Sciences,2009,36(1):2-12.

[10]Geller Robert J.Scaling relations for earthquake source parameters and magnitudes[J].Bulletin of the Seismological Society of America,1976,66(5):150l-1523.