东中国海大浪频率和极值波高统计分析

刘成，郑崇伟，李荣波，贾云龙

（1.91550部队，辽宁大连 116023；2.92538部队气象台，辽宁大连 116041）

1 引言

恶劣海况对航、海洋工程等有着重要影响，大风大浪能致使舰船失速、转向、上浪和摇荡，导致航行与操纵困难，严重时甚至造成灾害。深入研究我国近海的大浪频率具有重要的实用价值。邓兆青等[1]利用RAMS模式输出的20年风场驱动SWAN（Simulating WAves Nearshore）模式，对渤海近20年的海浪场进行了模拟研究，研究发现渤海极值波高的大值区位于渤海东南部海域（38°—39°N，119.5°—120.5°E），百年一遇极值波高能达到6.7 m。郑崇伟等[2]曾利用QN（QuikSCAT/NCEP）风场驱动WW3（WAVEWATCH-III）模式，对南海近10年的海浪场进行数值模拟，发现南海海浪场受季风影响显著，极值波高的大值区分布于南海北部海域。郑崇伟等[3-6]还曾利用WW3模式对南海的海浪场进行模拟，并统计了南海的浪级频率，研究发现1月份南海5级以上的浪出现频率较高，4月、7月、10月，大浪基本都只在南海北部、中部出现。本文以QN混合风场驱动目前国际先进的第三代海浪数值模式SWAN，对东中国海的浪级频率和极值波高进行模拟研究，为防灾减灾、航海、海洋工程等提供科学依据。

2 风场资料

本文以QN混合风场驱动SWAN模式，所谓QN混合风场，就是对美国国家环境预报中心（NCEP）分析数据和卫星散射计（QuikSCAT）观测数据进行时空混合分析的结果，其空间分辨率为0.5°×0.5°，空间范围覆盖全球，时间范围从1999年8月—2009年7月，每6 h一次数据，该风场具有很高时空分辨率和精度，被广泛用作海浪模式的驱动场[7-8]。

3 模拟方法、资料验证

3.1 模式简介

SWAN模式是由荷兰Delft理工大学在WAM模式的基础上发展起来的。通常用于近岸、湖泊以及江河口区，对谱型不做事先假定[9]。

在笛卡尔坐标系下，其控制方程通常采用如下形式：

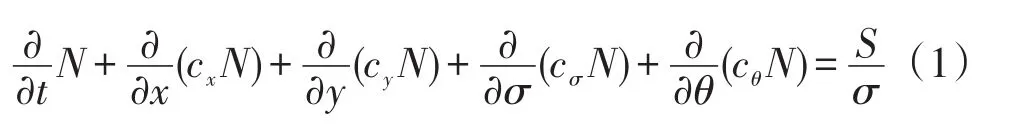
式（1）中，θ为波向，cx、cy分别为 x方向和y方向上的传播速度，cθ为波向空间的群速度，cσ为频率空间的群速度，S为源函数，它包括风能输入的线性增长和指数增长、白冠破碎引起的能量耗散、底摩擦耗散、波浪深度诱导破碎、三阶波-波相互作用和四阶波-波相互作用。近岸海浪由于海底地形复杂多变，因此一般需要考虑三波和四波之间的相互作用。从理论上讲，SWAN模式更适合于浅水区域。

3.2 模拟方法

以QN风场驱动SWAN模式，对近10年东中国海的海浪场进行数值模拟。选取计算范围为25°—41°N，117°—130°E，为了消除边界效应带来的影响，根据海浪具有“失忆”的特点，将计算范围在中国海的基础上稍微扩大，再从中截取所需要的东中国海范围。模式分辨率取0.15°×0.15°，计算时间从1999年08月01日00:00时—2009年07月31日18:00时，积分步长取300 s，每1h输出一次结果。

3.3 资料验证

本文将模拟结果与T/P高度计观测的有效波高（SWH——Significant Wave Height）进行比较，发现模拟的SWH具有很高的精度，这种方法也被前人广泛运用，证明是可行的[10-11]，本文通过验证发现模拟的海浪数据与观测资料较为接近，在此不再赘述具体验证过程。

4 大浪频率

利用模拟的近10年逐3h的SWH数据，对东中国海2、5、8、11月及全年的波浪等级频率进行了统计，主要列出了2.5 m以上大浪出现的频率，见图1、图2。波浪等级为国家海洋局公布的划分标准（见表1）。

2月（见图1a）：由低纬向高纬，大浪频率逐渐递减，长江口以北的等值线大致呈南北向分布，长江口以南的低纬度海域的等值线大致呈东北-西南向带状分布。渤海、黄海北部，以及我国近岸的大浪频率基本在3%以内，黄海中南部的大浪频率在3%—12%，到了东海，大浪频率迅速增加，并在琉球群岛附近海域达到最大，基本在21%以上，高值中心可达24%以上。

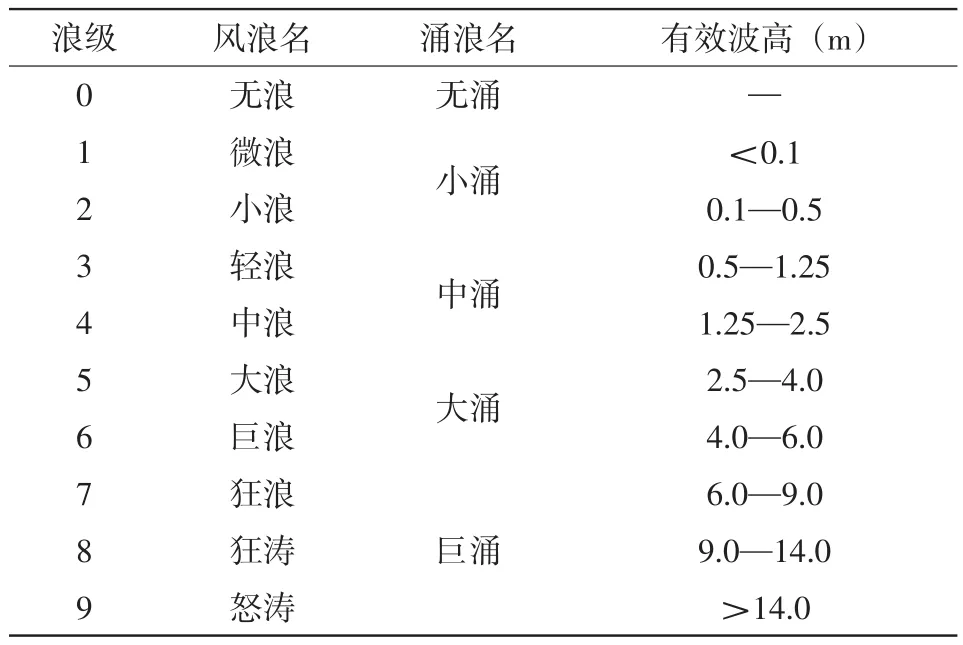
表1 波浪等级表

5月（见图1b）：各个海域的大浪频率在4个代表月中最低，基本在2.4%以内，这应该是由于该月冷空气已经明显变少，且强度很小，而偏南向的季风尚未盛行，导致该月的风速整体偏小。渤海和黄海大范围海域的大浪频率在0.3%以内，琉球群岛附近海域为相对高值中心。

8月（见图1c）：大浪频率较5月明显增加，但低于2月和11月，黄渤海的大浪频率较低，基本在2%以内，在东海，大浪频率的等值线大致呈圆形分布，高值中心分布于琉球群岛附近海域，中心可达14%以上。

11月（见图1d）：该月的大浪频率为4个代表月中最大，渤海、黄海北部，以及我国近海的大浪频率基本在5%以内，黄海中南部海域的大浪频率在5%—10%；等值线在东海大致呈东北-西南走向，大值区仍分布于琉球群岛附近海域，在20%以上，高值中心分布于台湾岛以东和东北部近海，可达35%以上。

从全年的大浪频率来看：高纬的大浪频率小于低纬，近岸的大浪频率小于离岸，西部海域的大浪频率小于东部海域。渤海、黄海北部、我国近海的全年大浪频率基本在2%以内，黄海中南部的全南大浪频率在2%—6%；东海的全年大浪频率在6%—20%，等值线呈东北-西南走向，大值区分布于琉球群岛附近海域，高值中心分布于台湾岛以东及东北部近海，达到16%以上。

5 最大波高、极值波高

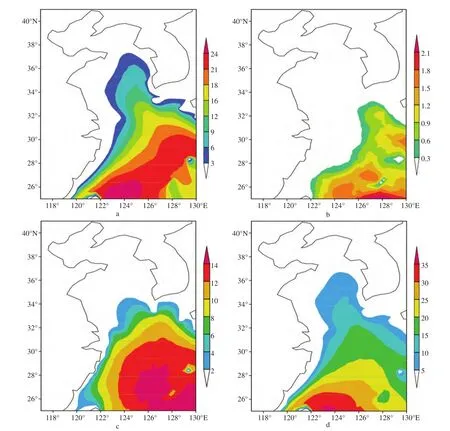
图1 东中国海2、5、8、11月的大浪频率（单位/%）

在海洋开发、航海等活动中对极值风速、极值波高都较为关注，郑崇伟等[12]曾利用CCMP（Cross-Calibrated,Multi-Platform）风场，采用Gumbel曲线法，推算了中国海的极值波高，发现五十年一遇和百年一遇极值风速的大值中心主要分布于琉球群岛附近海域、台湾以东洋面、南海北部海域；张德天等[13]曾利用QN混合风场资料，推算了中国海的极值波高，发现极值风速的大值中心都主要集中在台湾以东洋面、琉球群岛附近海域、海南岛以东和东沙群岛附近海域。

本文利用模拟的逐3h的SWH统计了近10年东中国海的最大波高分布特征，见图3；此外还参考郑崇伟、张德天等的计算方法，推算了东中国海30年一遇、50年一遇的极值波高，见图4。

5.1 最大波高

近10年期间，东中国海的最大波高整体表现出南大北小、离岸大近岸小的分布特征。沿岸的最大波高基本在3 m以内，渤海的最大波高在5 m以内，黄海北部的最大波高在6 m以内，在南黄海的西部近岸存在一相对大值区，最大波高在5—7 m，到了东海，最大波高明显增大，基本在5 m以上，琉球群岛附近海域基本在7 m以上，高值中心可达11 m，详见图3。琉球群岛附近海域的大浪应该是由于台风和冷空气的影响所致，该海域在夏季经常遭受台风袭击，冬季冷空气在海域相对开阔的海域，海浪也更容易充分成长，形成大浪。

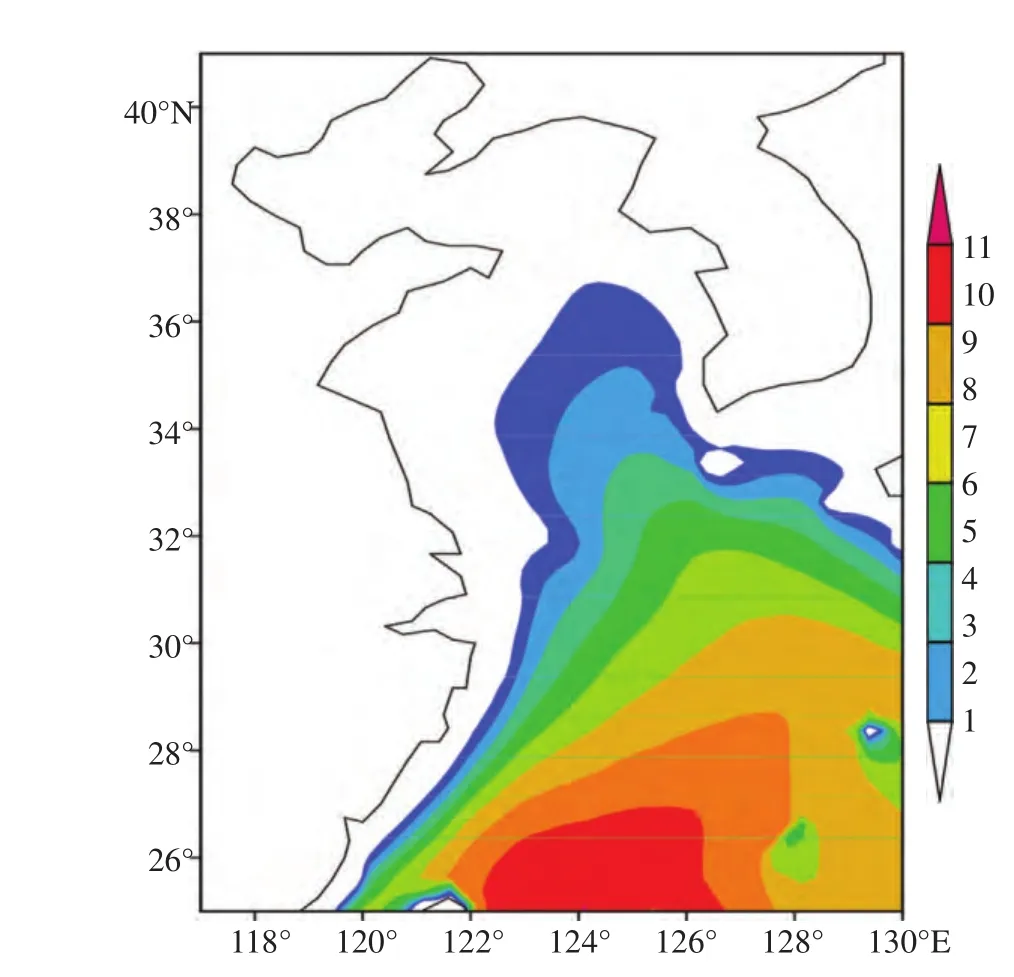
图2 东中国海全年的大浪频率（单位/%）

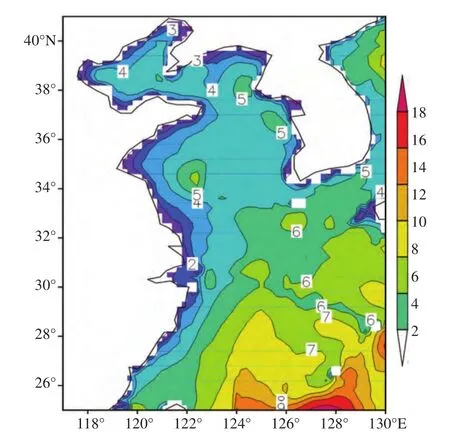
图3 近10年中国海的最大波高分布特征（单位/m）

5.2 极值波高

采用Gumbel曲线法[14-18]计算了东中国海的30年一遇、50年一遇极值波高，具体计算方法如下：

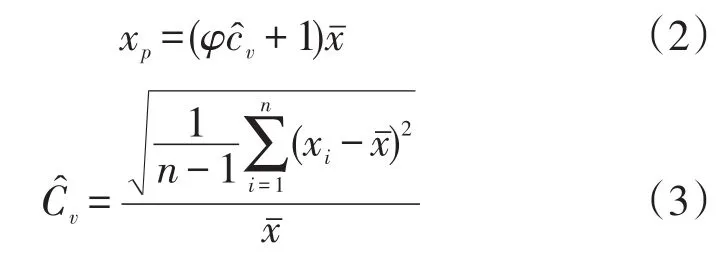
式（2）中，xp为所求多年一遇的极值，xˉ为均值，φ为离均系数，表2中P′为设计频率。

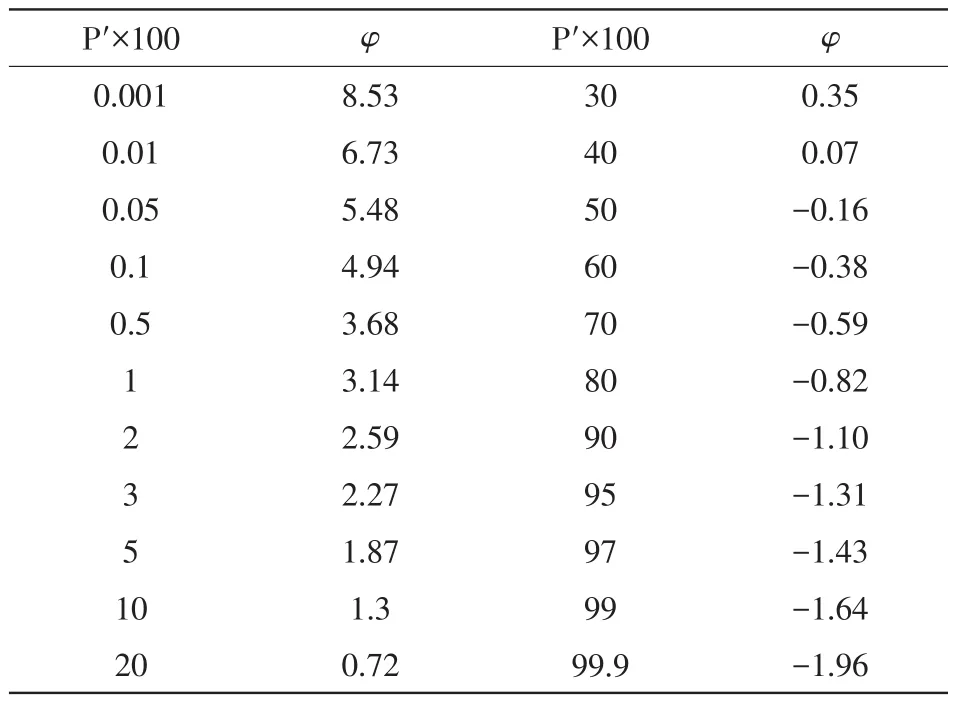
表2 耿贝尔曲线的离均系数

30年一遇极值波高（见图4a）：渤海的极值波高在5 m左右，等值线大致呈东北-西南走向；黄海的极值波高在4—8 m，等值线呈南北向带状分布，近岸小，离岸大；东海的极值波高明显大于黄渤海，该海域基本在9 m以上，大值区分布于琉球群岛附近海域，基本在11 m以上，高值中心可达13—15 m。

50年一遇极值波高（见图4b）：渤海中部的极值波高在5—7 m左右，近岸在3—5 m，等值线大致呈东北-西南走向；黄海北部的极值波高在5—7 m，等值线呈东西向带状分布，黄海中南部海域的极值波高在5—9 m，等值线呈南北向带状分布，近岸小，离岸大；东海的50年一遇极值波高等值线大致呈东北-西南向分布，基本在11m以上，大值区分布于琉球群岛附近海域，基本在13 m以上，高值中心可达15—17 m。

6 结论

（1）东中国海的大浪频率具有较为明显的季节特征和区域性差异：11月出现频率最高，基本在35%以内，2月稍次之，基本在34%以内，5月出现频率最低，在2%以内。高纬的大浪频率小于低纬，近岸的大浪频率小于离岸，西部海域的大浪频率小于东部海域；

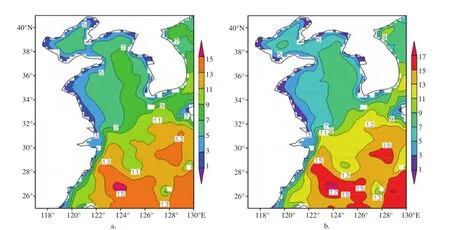
图4 中国海30年一遇、50年一遇极值波高（单位/m）

（2）近10年期间，沿岸的最大波高基本在3 m以内，渤海的最大波高在5 m以内，黄海北部的最大波高在6 m以内，在南黄海的西部近岸存在一相对大值区，最大波高在5—7 m，到了东海，最大波高明显增大，基本在5 m以上，琉球群岛附近海域基本在7 m以上，高值中心可达11 m；

（3）渤海的30年一遇极值波高在5 m左右，等值线大致呈东北-西南走向；黄海的极值波高在4—8 m，等值线呈南北向带状分布；东海的极值波高明显大于黄渤海，该海域基本在9 m以上，大值区分布于琉球群岛附近海域，基本在11 m以上，高值中心可达13—15 m。50年一遇极值波高的分布特征与30年一遇极值波高的分布特征较为相似，在数值上偏大。

[1]邓兆青,周良明,吴伦宇,等.渤海重现期波高的数值计算[J].海洋湖沼通报,2007(s):8-14.

[2]郑崇伟,周林.近10年南海波浪特征分析及波浪能研究[J].太阳能学报,2012,33(8):1349-1356.

[3]郑崇伟,李训强,潘静.近45年南海-北印度洋波侯统计分析[J].台湾海峡,2012,31(3):317-323.

[4]郑崇伟,周林.西沙、南沙海域波浪及波浪能季节变化特征[J].海洋科学进展,2011,29(4):419-426.

[5]郑崇伟,林刚,孙岩,等.近45年太平洋波浪特征分析[J].热带海洋学报,2012,31(6):6-12.

[6]郑崇伟,林刚,孙岩.近22年南海波浪能资源模拟研究[J].热带海洋学报,2012,31(6):13-19.

[7]徐艳清,尹宝树,杨德周,等.东中国海海浪数值模式研究[J].海洋科学,2005,29(6):42-47.

[8]李明悝,候一筠.利用QuikSCAT/NCEP混合风场及WAVEWATCH模拟东中国海风浪场[J].海洋科学,2005,29(6):9-12.

[9]李燕,薄兆海.SWAN模式对黄渤海海域浪高的模拟能力试验[J].海洋预报,2005,22(3):75-82.

[10]周兆黎,杨显宇.WAVEWATCH-III有效性检验[J].热带海洋学报,2008,27(2):1-6.

[11]齐义泉,朱伯承,施平,等.WAVEWATCH模式模拟南海海浪场的结果分析[J].海洋学报,2003,25(4):1-9.

[12]郑崇伟.基于CCMP风场的近22年中国海海表风场特征分析[J].气象与减灾研究,2011,34(3):41-46.

[13]张德天,郑崇伟,石岭琳,等.1999-2009年QN风场对中国海海表风场的研究[J].海洋预报,2011,28(4):58-64.

[14]郑崇伟,潘静,田妍妍,等.全球海域风浪、涌浪、混合浪波候图集[M].海洋出版社,2012.

[15]Zheng C W,Zhuang H,Li X,et al.Wind Energy and Wave Energy Resources Assessment in the East China Sea and South China Sea[J].Science China Technology Sciences,2012,55(1):163-173.

[16]Zheng C W,Zhou L,Huang C F,et al.The long-term trend of a sea surface wind speed and a(wind wave,swell,mixed wave)wave height in global ocean during the last 44 a[J].Acta Oceanologica Sinica,2013,32(10):1-4.

[17]Zheng C W,Shao Long-tan,Shi Wen-li,et al.An assessment of global ocean wave energy resources over the last 45 a[J].Acta Oceanologica Sinica,2014,33(1):92-101.

[18]Zheng C W.Assessing the China Sea Wind Energy and Wave Energy Resources from 1988 to 2009[J].Ocean Engineering,2013,65:39-48.