估价模型对新股估价的比较分析
李 博,燕 波
(汕头大学商学院,广东 汕头 515063)
一、引 言
在企业上市前,首先需要量化企业的价值,即对上市企业进行估价。新股定价是新股发行中最为核心的问题,也是投资银行等证券机构的核心任务所在,其涉及到新股发行过程中诸多参与方的利益。与已上市交易的股票价格是由市场所决定的价格形成机制不同,新股在一级市场的定价需要对二级市场的预期市场价格进行估计,为新股合理定价具有较大的难度,一个好的估价模型显得尤为重要。
由于各国证券市场环境的不同,将估价模型应用到新股定价中会碰到是否适用的问题。据笔者所知,国内缺乏对各种估价模型在我国应用的适用性分析,更缺乏将估价模型应用到新股发行中来的研究。多数研究直接采取拿来就用的做法,缺乏对我国股票市场实际情况和估价过程可能碰到的问题的分析。我们知道,新股定价是一个市场化定价的过程,何种估价模型的估价更能反映新股的预期市场价值,更能反映二级市场价格的变动,这些都是判断一个估价模型在实际应用中优劣的标准。我国长期以来使用固定价格定价模式,行政管制很大程度上造成了一、二级市场定价脱节,新股首日收益率极高。在新股定价市场化改革的今天,提供关于定价模型在应用性方面以及估价精确性方面的经验证据,具有很重要的现实意义。
二、相关文献综述
关于新股估价的研究可以回溯至资产定价这一课题。资产定价的核心思想为金融资产的价值或价格等于其预期收益的现值。按照这一思想,资产定价理论的发展可以大致划分为两个方向:第一个方向是寻求资产的绝对价格,即通过衡量某一资产的风险和预期收益而确定其价值。代表性的模型有股利贴现模型和现金流贴现模型。第二个方向是相对估价,即通过替代资产或其他衍生产品的价格来推断某一资产的价格。国内关于新股估价模型的研究很少,只有少数研究结合影响新股定价的因素建立回归模型对新股定价和首日收益进行预测,如白仲光和张维[1]应用随机边界模型实证检验了中国新股市场发行定价与新股上市后的市场定价是否存在定价过高或过低的现象。他们发现中国新股发行定价不存在类似于国外市场发现的随机上边界,相反从新股发行定价的统计分布上却可以得出存在着显著的下边界的现象,同时发现新股上市后市场定价同样存在显著的下边界,显示有部分新股上市后被市场高估。张岚[2]把定性分析和定量分析结合起来,在综合考虑新股上市定价的影响因素的基础上给出了三类新股定价模型,藉此对新股上市首日定价和上市后的合理定价进行预测。冯涛和王永明[3]在回顾以往定价理论的基础之上,试图通过对影响IPO定价的诸多因素的回归分析,建立一个IPO定价模型,并对之进行检验。其检验结果表明,该模型具有统计学意义,且可以有效地降低中国股市IPO折价率。总体而言,这些研究并未对相关估价模型进行深入分析和探讨,而国外关于股价模型的研究文献较多。
关于相对估价法和现金流贴现法在估价精确性方面的比较研究中,一方面,一部分研究认为一个好的现金流贴现模型在估价上与相对估价法都是有效的,具有相同程度的精确性,如Kaplan等[4]、Gilson等[5]。另一方面,Barker[6]认为,由于未来收益的不确定性和需要决定一个合理的折现率(资本成本),这会使得现金流贴现模型或股利贴现模型的应用变得很困难。Bradshaw[7]发现财务分析师很少使用计算现值的方法来估算权益资产的价值。Asquith等[8]对美国财务分析师的报告进行研究发现,几乎所有的分析师在使用基于收入的相对估价法,只有12.8%的分析师报告中使用了现金流贴现法。
除了讨论估价模型的选择和估价精确性的研究外,也有将估价模型应用到新股定价中来的研究。Kim等[9]基于美国新股发行样本对相对估价法进行了研究,他们发现如果采用历史数据来估算新股价值,所带来的精确性很差。但如果使用预测数据,如采用预期收益来计算市盈率(P/E),则会大大提高估价的准确性。Berkman等[10]以新西兰的45家上市公司作为样本发现,一个好的现金流贴现模型的精确性和基于市盈率(P/E)的相对估价模型的精确性是一样的。Purnanandam等[11]发现IPO公司相对于同行业的配对公司,其发行价被高估的程度达到14-50%,发行价被高估的IPO公司其首日收益率较高,其长期市场收益率较低。但Zheng[12]指出Purnanandam等[11]使用的相对估价法在计算IPO公司的内在价值时存在一些问题,致使IPO公司的内在价值被低估,当纠正估价模型的估价偏差后,新股的发行价并没有被高估。
Roosenboom[13]研究了法国的承销商如何定价新股,发现承销商会根据上市企业的特征、企业上市前整个股票市场的收益率和整个股票市场的波动率来选择新股估价方法。此外,承销商会根据企业特征对不同估价方法得出的估价结果赋予不同的权重来最终决定IPO企业的内在价值。最后,承销商往往会结合实际情况来制定一个低于企业内在价值的发行价。Roosenboom[14]同样通过分析228份法国承销商的报告,研究承销商如何来确定IPO企业的内在价值。研究结果表明,承销商通常使用乘数估价法、股利贴现模型和现金流贴现模型来决定IPO企业的内在价值,但这些模型估计出来的内在价值相对于IPO企业的实际市场价值存在一个正的偏差。但承销商在决定IPO发行价时,会故意设定一个低于内在价值的发行价格,IPO首日超额收益主要来源于承销商的故意低价发行。Aggarwal等[15]的研究发现在IPO企业定价时,企业盈余与其价值并不是一种简单的线性关系,亏损较多的企业相对亏损较少的企业其估价更高,盈利较多的企业相对盈利较少的企业其估价更高。研究结果表明IPO企业亏损可能是互联网企业成长能力的一个代理指标,是构成IPO企业价值的重要组成部分。Shu等[16]以台湾的287家IPO公司为样本,发现大多数IPO公司的发行价定价过高,发行价相对内在价值的定价水平与首日收盘价的定价水平成正相关关系。此外,IPO企业的盈余管理水平尽管和发行价的定价水平无相关关系,但和首日收盘价的定价水平和新股的长期市场表现弱势正相关。
三、估价模型介绍与研究假设
(一)相关估价模型介绍
本文主要介绍和比较的两个具有代表性的估价模型:剩余收益模型和相对估价模型。其中,剩余收益模型寻求资产的绝对价值,而相对估价模型则计算资产的相对价值。
1.剩余收益模型
剩余收益模型是从股利贴现模型推导出来的衍生模型。由于现金流贴现模型和股利贴现模型在现实应用中,会碰到难以预测未来的自由现金流和股利的问题,而剩余收益模型能将企业的价值与会计数据联系起来,从而给估价带来了方便。
剩余收益模型的表述如下:
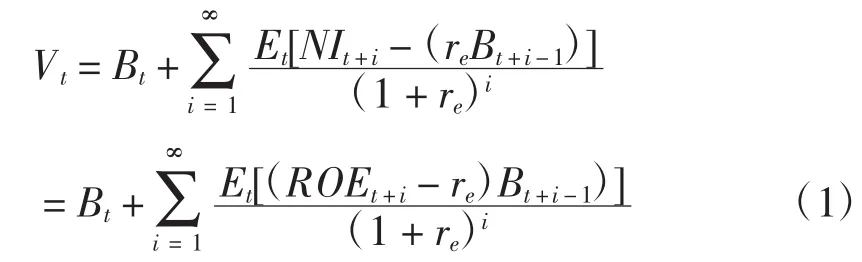
其中,Bt为企业在时期t净资产的账面价值,Et[.]是基于时期t所能获得的信息而得到的期望值,NIt+i是企业在t+i期的净收益,re是权益资本成本,ROEt+i是企业在t+i期的净资产收益率,即净收益除以净资产的账面价值。
在实际模型估计中,公式(1)中的无限期未来剩余收益的现值可以用固定期数(i)的剩余收益的现值加上一个永续年金终值来代替。Lee等[17]发现当固定期数(i)超出三年时,模型的估计精度对固定期数的选择不敏感。即当固定期数为3年或三年以上,模型期数的选择不会显著影响内在价值的估计。按照Lee等[17]和Dong等[18]的做法,公式(1)可以表述成一个三年期的估价模型:
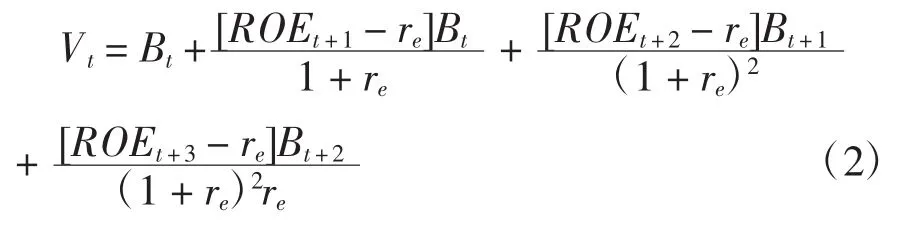
其中,ROEt+i是预期在第t+i期的净资产收益率;Bt+i是第t+i期的净资产账面价值;re为权益资本成本;式(2)中最后一项是以永续年金形式计算的第t+3期后的剩余收益的折现值。
本文采用CAPM模型来估计新股的权益资本成本,即:

在CAPM计算过程中,采用两种风险系数(β)来计算权益资本成本(re)。首先使用上市后个股的风险系数来计算权益资本成本。每家IPO公司的风险系数由上市后三年的月收益率计算。同时也使用行业平均风险系数来计算IPO公司的权益资本成本。即取IPO公司所在行业的公司的风险系数的平均值,其中IPO公司所在行业的公司风险系数由IPO公司上市前12个月的行业公司日收益率计算。
由于缺少关于我国市场风险溢价的研究,本文按照Kaplan等[4]、Lee等[17]和Dong等[18]的做法,使用1992-2010年的股票市场收益率减去相应5年期国债年收益率的平均值作为市场风险溢价(E(rm)-rf),计算得到的年市场风险溢价为8.06%。
2.相对估价模型
相对估价法又称乘数估价法,是指在市场上找出一个或几个与目标企业相同或相似的参照企业,分析、比较目标企业和参照企业的相关财务指标,在此基础上,修正、调整参照企业的价值,最后确定目标企业的价值。
本文基于企业的规模、盈利能力和成长性三个基本面来选择参照企业。具体而言,对于每家IPO企业,首先选择与其在相同行业的公司,然后剔除上市时间少于三年的公司,在剩余的可选择公司中,选择那些与IPO企业在销售额(规模)和销售收益率(盈利能力)这两项指标上绝对误差小于30%的公司,最后再在这些剩下的可选择公司中,选择一个在净利润增长率(成长性)方面最相近的公司作为参照公司。之所以选择同行业的公司作为参照公司,是因为同行业的公司中最有可能找到在营运风险、盈利能力和成长性方面与IPO公司相近的公司。而选择上市时间不少于三年的公司则是为了尽量避免选择新股作为参照企业。如果30%的选择误差过于严格导致相应的IPO企业不能找到与之配对的参照企业,则将这绝对误差放松到50%。
在为IPO公司选取了相应的参照公司后,本文按照Purnanandam等[11]的方法,分别计算参照公司的三个定价乘数比:每股价格对每股销售收入的比率(P/S)、每股价格对每股总利润的比率(P/T)和每股价格对每股净利润的比率(P/E)。IPO公司的内在价值可以表示为参照公司的定价乘数乘以IPO公司的相应财务指标。比如,当使用P/S比率计算IPO公司的内在价值时,IPO公司的内在价值为参照公司的P/S比率乘以IPO公司的每股销售收入。基于三个定价乘数的新股估价公式具体计算如下:


其中,(P/S)Match是参照公司在IPO公司上市前两个月的平均市场价格除以在IPO上市年度的每股销售收入,其中每股销售收入为销售收入除以总股本。SIPO是IPO公司预期在上市年份的每股销售收入。之所以使用预测数据是因为Kim等[9]发现使用预测数据估价的精确性比使用历史数据估价的精确性更高。以此类推,基于其他两个定价乘数的估价公式与此类似。
(二)研究假设
新股估价过程就是通过了解二级市场的信息,制定一个尽量和二级市场接轨的发行价格的过程。所以,在一定程度上,判断一个估价模型的估价是否精确,可以通过分析其估价是否和实际市场价格相接近而得到。一个好的估价模型其对新股的估价应当与新股的实际市场价值相差较小,估价结果集中在实际市场价值附近,即估价的无偏性和有效性程度均较高。
由于我国的证券市场是一个处于转轨中的新兴资本市场,在二级市场是否达到弱势有效这一问题上,许多学者对此仍存在争议。我国证券市场发展的初期定位于为国企服务的融资市场而非投资市场,在机构投资者的培育和制度的建设方面均起步较晚,故在相关法律法规保障、市场投资者结构以及投资者素质等方面,与成熟资本市场相比均还存在不足。我国的证券市场一度被贴上“投机市”的标签,股市的高市盈率现象长期存在,A股的价格明显高于相应的B股价格和H股价格,许多学者认为我国证券市场的股价水平存在系统性泡沫,即上市公司的市场价格长期大幅度偏离于其内在价值(或理论价值)。在这种情况下,由于市场泡沫的存在,而相对估价法使用可比公司的价值来估算新股的价值,将比剩余收益模型的估价更贴近市场价值,估价偏差最小。而基于股利贴现模型推导出来的剩余收益模型衡量的是新股的理论价值,其估价很可能小于新股的预期市场价值,估价偏差最大。故我们提出以下研究假设1:
假设1:与剩余收益模型相比,相对估价模型对新股上市后的市场价值的估价偏差最小,有效性最高(估价区间相对集中)。
一个好的估价模型不仅在估价上的偏差很小,同时其估价也应该随着预期市场价格的波动而波动。由于相对估价模型采用可比公司的价格来估算新股的价值,其更能反应二级市场行情对新股预期市场价格的影响。所以,我们提出假设2:
假设2:与剩余收益模型相比,相对估价模型的估价更能解释新股上市后市场价格的变动。
四、相关模型对新股估价的实证分析
(一)样本选取
本文所用到的财务数据的时间跨度为1996-2011年,由于要用到上市后三年的市场数据和财务数据,故以1996-2008年发布上市公告的公司为样本。之所以选取从1996年开始的IPO公司为样本是为了保证有足够的可选择公司来进行配对,以确保在使用相对估价法估价时能找到相应的配对公司。同时,1996年前我国的股票市场刚建立不久,市场不够成熟,新股的发行以国家配给为主,许多新股以面值发行,剔除这部分数据有利于保证样本的一致性和可对比性。此外,由于需要用到上市后三年的数据,本文选择到2008年年底为止发布上市公告的IPO公司。本文初始样本为1253家在A股主板市场上市的企业,剔除曾发行过B股和H股的公司和金融保险行业类公司,再剔除数据缺失的公司,最终样本为1148家IPO公司。数据主要来源于CSMAR和RESSET数据库。
(二)模型对新股估价的精确性分析
1.估价精确性的描述性分析
由于新股的估价是以二级市场的期望市场价格为基准,新股估价过程就是通过了解二级市场的信息,制定一个尽量和二级市场接轨的价格的过程。在一定程度上,判断一个估价模型的估价是否有效,可以通过分析其估价是否和实际市场价格接近而得到。此外,由于新股上市后的短期市场价格可能受非理性因素(如:异质信念)的影响而产生偏离,故本文选择新股从上市后第三个月至第六个月这三个月的平均市场价格作为模型估价的参照价格。具体而言,对每一家上市企业,分别计算模型估价值相对于新股上市后平均市场价格的比率来衡量模型的估价偏差,如果该比率大于1,表明模型估价高估了新股的价值;如果该比率小于1,则表明模型估价低估了新股的价值。模型估价偏差用DIF表示,即:DIF=模型估价值/平均市场价格。表1列出了新股发行价、上市后平均市场价格和两个估价模型的估价偏差(DIF)的中值,括号内为模型估价偏差(DIF)的中值是否等于1的Wilcoxon检验Z值。
表1的结果表明,在整个样本区间内,基于剩余收益模型和相对估价模型对新股的估价的中值均显著小于新股上市后的平均市场价格。基于两个风险系数的剩余收益模型的估价偏差的中值分别为0.17和0.16,远远小于1,表明剩余收益模型的估价大大低估了新股的价值。而基于三个定价乘数的相对估价模型的估价偏差的中值在0.9以上,与1较为接近,表明相对估价模型的估价与新股上市后的市场价值较为接近。此外,从各IPO年份的统计值来看,剩余收益模型的估价偏差亦明显大于相对估价模型的估价偏差,而相对估价模型的估价与新股上市后市场价格较为接近。
为进一步分析两个模型的估价偏差,本文按照Kaplan等[4]的方法,通过对模型的估价偏差比率(DIF)取自然对数来减少极值的影响。我们知道,log(模型估价值/平均市场价格)=log(模型估价值)-log(平均市场价格)。如果偏差比的自然对数大于0,则表明,相对于上市后市场价格,估价模型的估价过高,反之则估价过低。表2报告了相对于上市后市场价格,两个估价模型的估价偏差的自然对数的统计值。
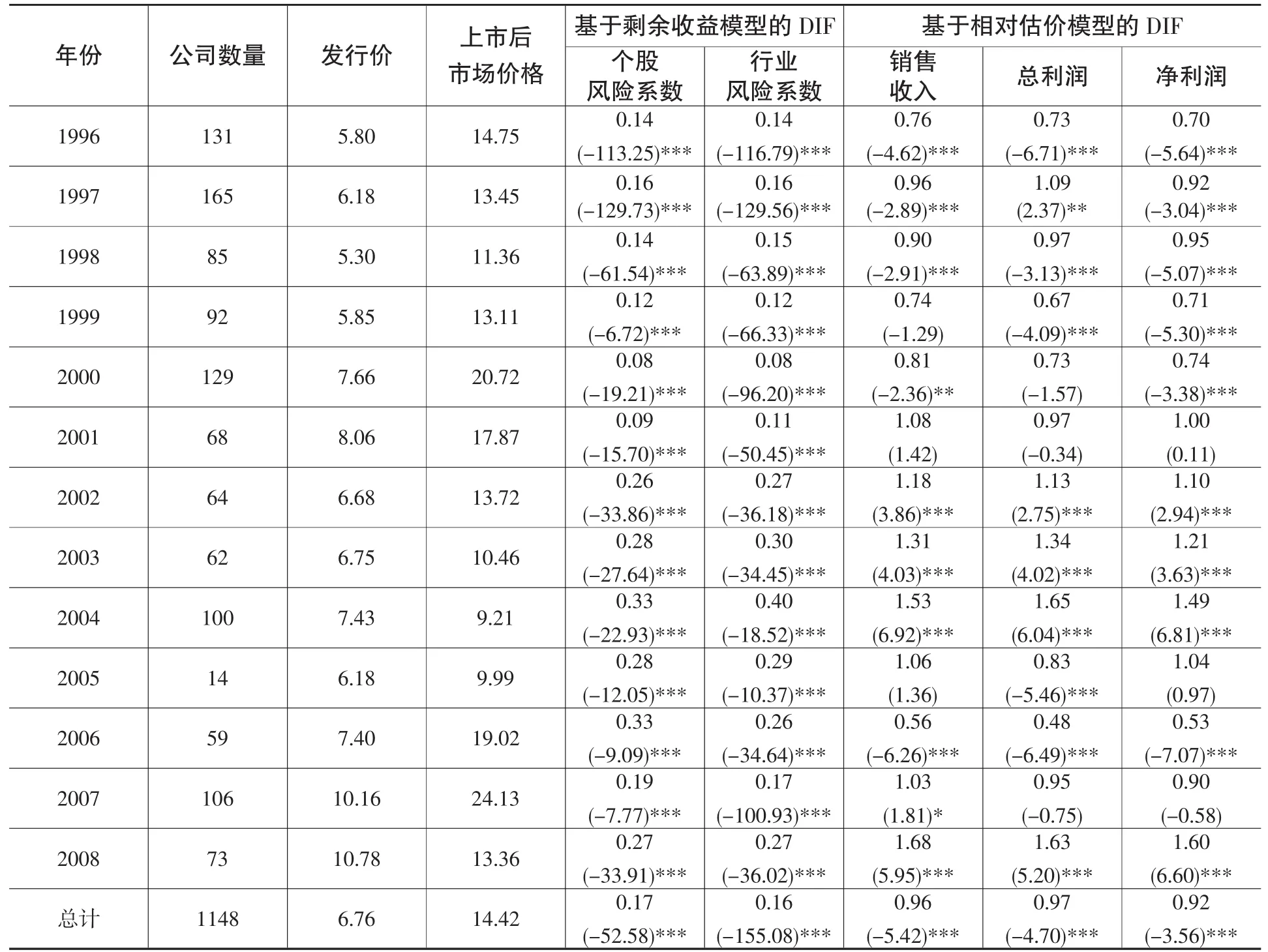
表1 新股发行价、上市后市场价格和模型估价偏差的年度中值统计
如表2所示,当使用基于个股风险系数的剩余收益模型来估计新股价值时,相对于上市后市场价格,模型估价偏差的自然对数的均值为-1.932,其中值为-1.801,意味着模型在很大程度上低估了新股的市场价格。当使用行业平均风险系数来计算剩余收益模型时,估价偏差没有明显变化,其均值和中值分别为-1.943和-1.804,估价偏差仍然很大。相对于上市后市场价格,相对估价模型的估价精确性最高,其中又以销售收入为定价乘数的估价最为准确。基于销售收入的相对估价模型,其取对数后的估价偏差的均值和中值分别为-0.052和-0.042,远低于剩余收益模型的估价偏差。
从估价偏差的均值和中值,我们可以看出估价的偏差。而从估价的标准差和四分位距可以看出估价的有效性,即样本公司的模型估价是否向市场价格靠拢。从表2可以看出,剩余收益模型的估价有效性最差,其估价偏差的标准差为1.054,四分位距为1.071。同时,使用行业风险系数时,估价的有效性有所提高,估价偏差的标准差和四分位距有所降低。估价有效性最高的估价模型为相对估价模型,相对估价模型的估价更趋向于上市后的市场价格,其估价误差的标准差为0.574,小于剩余收益模型的值。
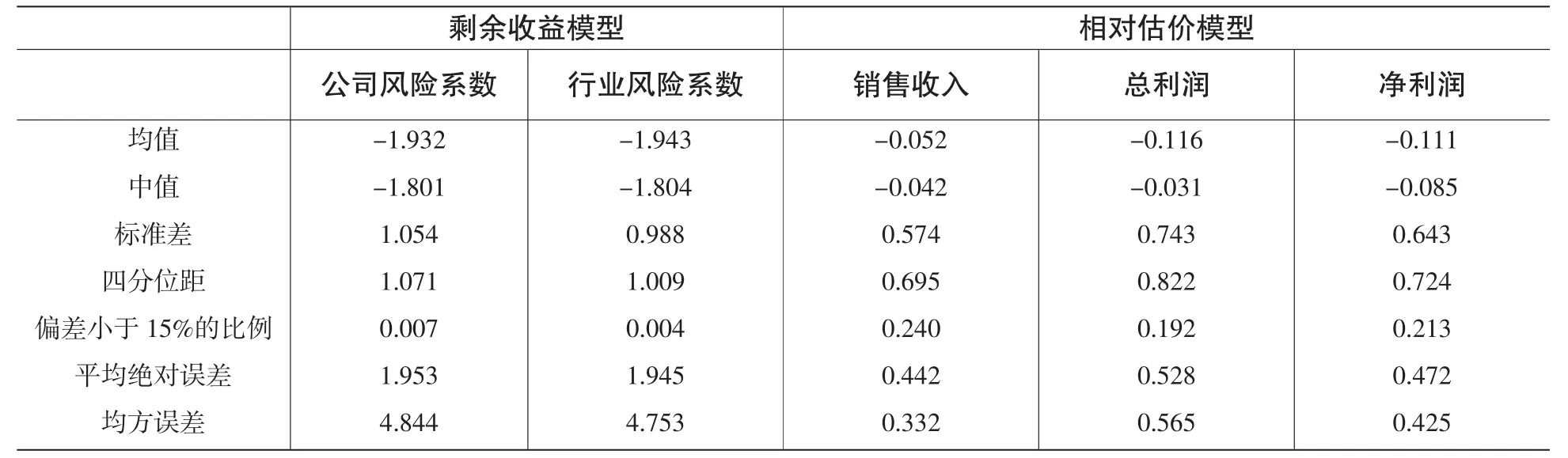
表2 模型估价偏差的描述性统计
同时,本文计算了样本公司中去自然对数后的估价偏差的绝对值小于15%的样本占总样本的比例。在系统偏差相近的情况下,一个好的估价模型其大部分估价应当集中分布在上市后市场价格左右。如表2所示,对于剩余收益模型,当使用个股风险系数时,只有0.7%的样本的估价位于15%的偏差范围内。而使用相对估价模型时,有近20%的样本公司的估价偏差小于15%,尤其当使用销售收入作为定价乘数时,有24%的样本公司估价偏差小于15%。
最后,表2给出了估价绝对误差的平均值和均方误差。这两个统计量基于不同的误差成本假定。平均绝对误差假定估价误差的成本与误差之间的关系是线性的,而均方误差则假定误差成本是估价误差的平方。两个统计量的结果表明,剩余收益模型的误差成本最大,其样本均方误差值大约在4.8左右,而相对估价模型的均方误差最小,在0.4左右。
总之,以上的结果支持假设1,对于上市后市场价格的估价,剩余收益模型在估价的整体偏差,有效性等方面的表现最差,其估价的偏差最大,估价分散,而相对估价模型的表现相对与剩余收益模型有明显改善。同时,在一定程度上,使用行业平均风险系数有利于提高模型的估价表现,而使用销售收入为定价乘数的相对估价法的表现最好。
2.估价精确性的回归分析
前面的分析比较了两个估价模型的估价与上市后市场价格之间差异。然而,一个估价模型在估算上市后的价格时可能是无偏的,但并不意味着其估价能很好地解释上市后市场价格的变动。一个好的估价模型不仅在估价上的偏差很小,同时其估价也应该随着预期市场价格的波动而波动。所以,下面将对上市后市场价格对模型估价做回归分析,分析比较模型估价对上市后市场价格的解释能力。
本文通过下面的回归模型分析模型对新股的估价对上市后市场价格变动的解释能力:

如果模型估价是对新股上市后价格的无偏估计,则上述回归的截距项(α)应当等于0,而回归系数(β)应当接近于1。考虑到回归模型中的截距项和残差项可能受极值的影响,首先对模型估价和上市后市场价格做自然对数转换,再进行回归。
表3报告了上市后市场价格的自然对数对各模型估价的自然对数的回归结果。由于截距项是否等于0和斜率项是否等于1的检验t值可以由回归系数与回归系数的标准误差计算得到,回归系数的标准误差更有助于判断模型估价的准确程度,故表中选择报告了回归系数的标准误差。如当使用基于个股风险系数的剩余收益模型来估计新股价值时,模型估价对市场价格的回归截距为2.585,截距的标准误差为0.018,则截距项是否等于0的检验t值为143.6,表明截距显著大于0。回归系数为0.157,回归系数的标准误差为0.013,则回归系数是否等于1的检验t值为-64.8,表明回归系数显著小于1。从结果可见,两个模型估价的回归截距项显著不等于0,且回归系数显著不等于1。但与前面的结果一致的是,在两个估价模型的比较中,剩余收益模型估价的回归截距项的t值(检验截距系数是否等于0)最大,表明其估价的系统偏差最大。同时剩余收益模型估价的回归斜率项的t值(检验斜率系数是否等于1)亦显著大于相对估价模型的相应t值,这表明剩余收益模型的估价在解释上市后市场价格波动时的解释能力较差。两个估价模型中,相对估价模型的估价能较好地解释上市后市场价格的变动,其回归系数为0.440(以销售收入为定价乘数),大于剩余收益模型的回归系数。同时,其调整后的R方为0.275,表明其估价能解释上市后市场价格27.5%的变动,明显大于剩余收益模型的解释能力。

表3 模型估价的回归结果分析

表4 经公司规模调整后的回归结果分析
Kaplan等[4]认为在使用模型估价时,回归模型中的截距项和残差项还可能受公司规模的影响。本文按照他们的做法,对上市后市场价格和模型估价进行规模调整,即除以上市前一年的销售收入,然后分别取自然对数,再进行回归分析。其相应的回归模型如下所示:
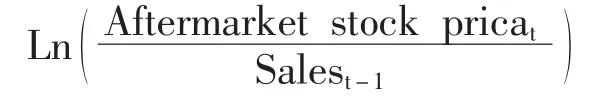

表4的结果表明,经规模调整后,两个模型估价的回归结果有明显改善,其模型估价对上市后市场价格的解释能力有明显提高,剩余收益模型的估价的解释能力在45%左右,而相对估价模型的估价对上市后市场价格的解释能力在70%以上,高于剩余收益模型的解释能力。此外,相对估价模型估价的回归系数为0.866,大于剩余收益模型的回归系数值,接近于1。以上结果表明,相对于剩余收益模型,相对估价模型的估价效果更好,假设2得到实证结果的支持。
五、结论
本文比较分析了相对估价模型和剩余收益模型的估价与上市后市场价格的差异。研究结果表明,尽管两个模型都存在一定的估价偏差,但是基于会计数据的剩余收益模型对新股的估价与新股上市后的市场价格差异较大,相对估价模型对新股的估价与新股上市后的市场价格较为接近。在对比分析中,相对估价模型的估价不仅偏差小、有效性较高,且能较好地解释上市后市场价格的变动。关于剩余收益模型在新股估价过程中精确性较低的结论可能是由于下述原因引起的:我国是一个处于高速发展中的新兴国家,投资者对未来企业发展前景较为看好,二级市场的市盈率较高。这样,基于会计数据的剩余收益模型很可能低估新股的上市后价格,给估价带来偏差。
总之,由于不需要事后财务和价格数据,相对估价模型在新股定价中应用更为方便,具有较高的可操作性。从估价的目的来看,新股定价的主要目的就是预测和估计新股在二级市场的价格,进而制定一个合理的发行价。而相对估价模型的估价与上市后市场价格最为接近,估价有效性较高,是估价模型中表现最好的模型。
[1]白仲光,张维.基于随机边界定价模型的新股短期收益研究[J].管理科学学报,2003(6):51-67.
[2]张岚.新股上市首日定价及上市后合理定价模型介绍[J].当代财经,2003(4):59-62.
[3]冯涛,王永明.中国证券市场IPO定价模型及其实证研究[J].统计与信息论坛,2009(24):58-61.
[4]Kaplan,S.N.and R.S.Ruback.The Valuation of Cash Flow Forecasts:an Empirical Analysis[J].Journal of Finance,1995,50(4):1059-93.
[5]Gilson,S.C.,E.S.Hotchkiss and R.S.Ruback.Valuation of Bankrupt Firms[J].Review of Financial Studies,2000,13(1):43-74.
[6]Barker,R.The Role of Dividends in Valuation Models Used by Analysts and Fund Managers[J].The European Accounting Review,1999,8(2):195-218.
[7]Bradshaw,M.The Use of Target Prices to Justify Sell-Side Analysts’Stock Recommendations’[J].Accounting Horizons,2002,16(1):27–41.
[8]Asquith,P.,M.Mikhail and A.Au.Information Content of Equity Analyst Reports[J].Journal of Financial Economics,2005,75(2):245-82.
[9]Kim,Moonchul and Jay R.Ritter.Valuing IPOs[J]. Journal of Financial Economics,1999,53(3):409-437.
[10]Berkman,Henk,Nichael E.Bradbury and Jason Ferguson.The Accuracy Of Price-Earnings And Discounted Cash Flow Methods Of IPO Equity Valuation[J].Journal of International Financial Management and Accounting,2000,11(2):71-83.
[11]Purnanandam A.K.and B.Swaminathan.Are IPOs Really Underpriced[J].Review of Financial Studies,2004,17(3):811-848.
[12]Zheng,StevenX.AreIPOsReallyOverpriced[J]. Journal of Empirical Finance,2007,14(3):287-309.
[13]Roosenboom,Peter.How Do Underwriters Value Initial Public Offerings?An Empirical Analysis Of The French IPO Market[J].Contemporary Accounting Research,2007,24(4):1217-1243.
[14]Roosenboom,Peter.Valuing And Pricing Ipos[J]. Journal of Banking&Finance,2012,36(6):1653-1664.
[15]Aggarwal,Rajesh,Sanjai Bhagat and Srinivasan Rangan.The Impact Of Fundamentals On IPOs Valuation[J],Financial Management,2009,38(2):253-284.
[16]Shu,Pei-Gi,Sue-JaneChiangandHsin-YuLin. Earnings Management,Managerial Optimism,And Ipo Valuation[J].Journal of Behavioral Finance,2012,13 (2):147-161.
[17]Lee,Charles M.C.,James Myers and Bhaskaran Swaminathan,What Is The Intrinsic Value Of The Dow[J].Journal of Finance,1999,54(5):1693-1741.
[18]Dong,Ming,David Hirshleifer,ScottRichardson and Siew Hong Teoh.Does Investors Misvaluation Drive The Takeover Market[J].Journal of Finance,2006,61(2):725-762.

