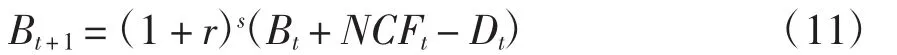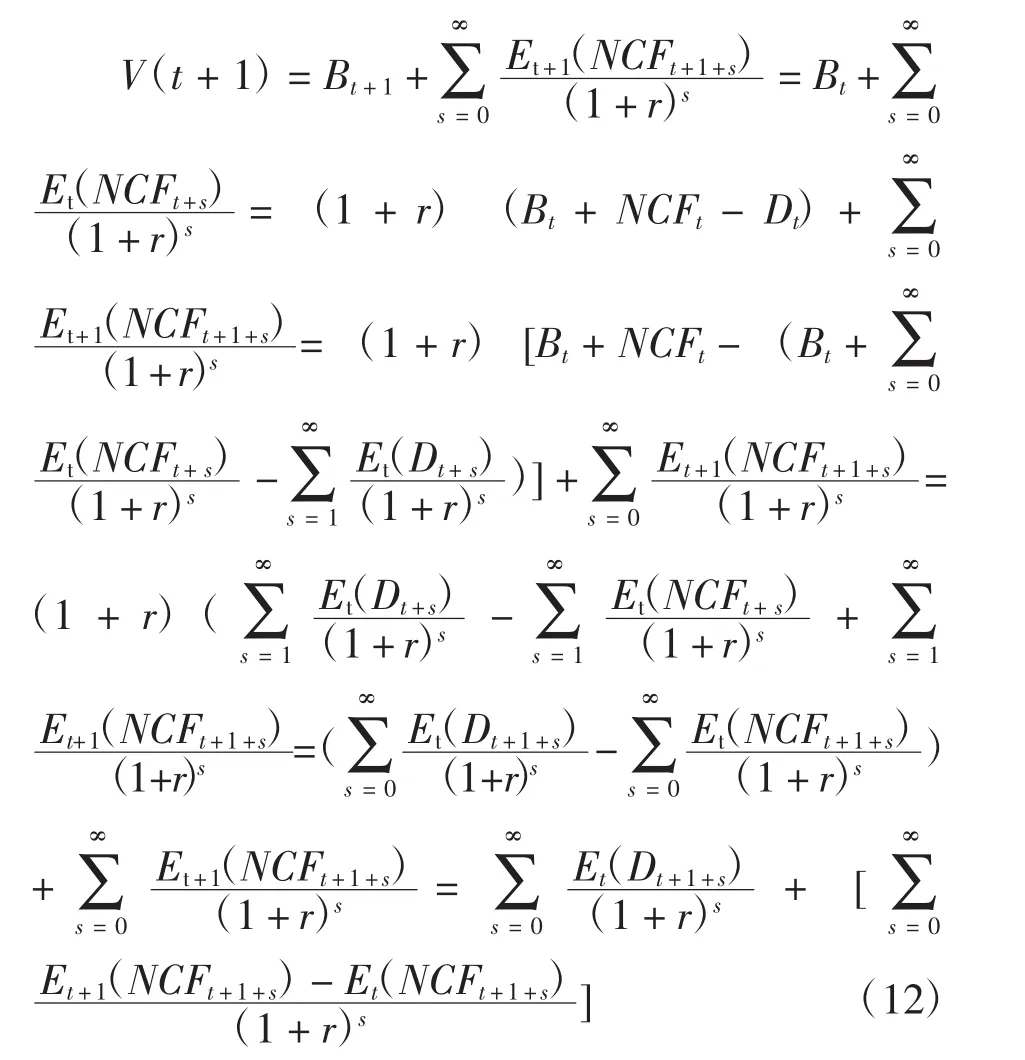股票价格波动的价值回复模型
林 祺,林 僖
(1.中山大学岭南(大学)学院金融系,广东 广州 510275;2.中国工商银行上海市分行,上海 200120)
一、引 言
股票价格决定理论一直都是现代金融经济学理论研究的核心问题之一。股票价格的波动遵循何种分布、有无规律可循,关系到股票价格的确定及股权类金融衍生产品的定价问题。因此,对股票价格波动行为问题展开深入研究具有重要的理论与现实意义,它将为各种以股票为标的资产的金融衍生工具的运用提供重要的定价参考依据。
关于股票价格波动行为的研究由来已久,国内外学者已对股票价格的波动行为提出了各种理论解释。对股票价格波动行为的文献,最早是从Cootner[1]对股票价格的“随机游走假说”的模型描述开始的。自Cootner这一开创性的研究之后,股票价格的波动服从“几何布朗运动”这一假设在现代金融经济学的分析中得到广泛应用。Fama[2]的研究得出,股票价格收益率序列在统计上不具有“记忆性”,所以投资者无法根据历史的价格来预测其未来的走势。Black and Scholes[3]在此基础上提出了著名的Black-Scholes微分方程及欧式看涨期权的解析解,为股权类衍生工具的定价开启了先河。Richardson and Smith[4]对股票收益率服从多元正态分布进行了实证研究,其认为股票收益率和市场模型参差是非正态分布的,这种非正态分布既出现在资产收益率的边际分布中,也出现在资产收益率的联合分布中。Trabelsi和Oueslati[5]使用突尼斯证券交易市场的数据,对股票价格基于新信息的动态调整现象进行了研究,结果表明基于 Amihud和 Mendelson(1987)、Damodoran(1993)、Brisley和Theobald(1996)的股价行为模型不能很好地解释新兴证券市场不同时期各种证券对新信息的过度反应现象。Vagnani[6]研究了基于Black-Scholes模型的隐含波动率微笑的问题,并在不确定世界中对Black-Scholes模型的机构化含义进行了深入的分析,同时运用模型模拟、实证研究和数学推导等方法,得出波动率微笑与交易者的行为有关的结论。
国内关于股票价格的波动性质的研究起步较晚,且国内现有的大部分研究主要集中在股票价格波动分布的研究上。翟爱梅等[7]借助力学领域中的塑性理论,建立了基于价格和成交量的股价塑性模型,得出被锁定的流通股数量越大,股价塑性系数就越大。根据对个股不同时段塑性系数的比较,可以识别流通股有无被锁定的现象。赵巍和何建敏[8]在股价收益的时变性和波动的长记忆性两个方面的基础上,得到了分数市场环境中的期权定价模型,并证明了布朗运动和Ornstein-Uhlenback过程驱动的期权定价模型均是分数市场环境中的期权定价模型的特例,并通过算例验证了长记忆参数H是期权定价中不可忽略的因素。余文利等[9]提出一种新的基于HMM的股票价格预测的方法,采用CBIC算法自动确定HMM隐状态数,并建立相应的HMM以进行单步值预测。通过与Hassan等人的HMM fusion model方法、ARIMA方法进行了比较,实证表明所提出的预测算法在股票价格预测中,比现有的不更新模型的方法能得到更好的结果。此外,代表性的还包括林勇和郭林军[10]、范申等[11]、顾钰[12]和马永亮等[13]等人的研究。
从现有文献来看,大部分文献主要集中在研究股票价格波动分布上,对有关股票价格与其内在价值相关关系的深入研究仍然较少。因此,对于股票价格与其内在价值相关关系问题做进一步深入研究就具有十分重要的理论和现实意义。这将有助于加深我们对股票价格波动性质的深入理解。有鉴于此,本文尝试着在传统金融经济学股票价格波动服从几何布朗运动的假设基础上进行修正,力图使股价的波动有一个更完整的理论基础。本文摒弃了传统股价波动模型关于股价期望收益率恒定不变的假定,建立了股票价格波动的价值回复模型,并在此基础上对股票价格的期望收益率进行了内生化处理,并推导了上市公司价值的波动模式,以便更好地理解现实中股票的价格波动现象和为现实中的股票和股权类金融衍生产品进行定价。
二、传统股票价格波动遵循几何布朗运动假设的局限性
长期以来,我们研究股票的价格波动时总是习惯从经典的假设开始,即股票价格的波动服从几何布朗运动。正是由于股票价格的波动是遵循Markov过程,因此股票价格的波动是无自相关的,当前的股票价格无助于预测未来的股票价格。Markov性质隐含了在将来任一特定时刻股价的概率分布与股票过去特定的运动路径无关的假定,因此Markov过程其实与证券市场是弱势有效是相一致的。
首先,在Markov过程的前提下,我们假设股票价格的期望收益率为μ,波动率为σ,则股票价格的波动可以表示为dS=μSdt+σSdz。由于股价的增长率服从均值为μ,标准差为的正态分布,因此其波动具有随机性。然而,假设股价存在长期的增长趋势,即股价以期望收益率μ增长,这一假设存在局限性,因为其只考虑了影响股票价格的一些外生因素,而忽视了股票价格的基本决定因素——股票的内在价值。股票的内在价值是公司基本面决定的本身所固有的价值,可表示为VP(t)=,V(t)为公司的价值,其等于公司的权益价值与公司的负债价值之和,即V=E+ L。因此,股票的价格绝不会长久地偏离其公司的每股价值,否则有效市场上的套利活动就会将股票的价格拉回到其合理的价格水平上,即股票的价格会不断地向其价值回复,本文把这种现象称之为股票价格的价值回复(value reversion)。而在dS=μSdt+σSdz中,我们看不到任何有关公司价值的信息,更看不到任何股票价格的价值回复的信息。
其次,虽然股票的价格会随着经济大趋势的波动而上下波动,甚至会出现暴涨暴跌的极端情况;但是,如果我们把时间放得长一点,就会发现股票的价格并不是在没有规律地上下波动,而是稳定地围绕着公司的价值上下波动。当公司的价值上升时(如超过预期的盈利,开发了某种至今还未被发现的潜在需求来满足消费者的需求等),股票的价格会趋于上升。相反,当公司的价值下降时,股票的价格也会跟着趋于下降。从长期来看,随着公司的成长,公司的价值是不断增长的,所以股票的价格也会跟着公司价值的增长而不断地上升,围绕其价值波动(虽然期间可能会由于外生的因素影响而出现短暂的偏离),并不断向其价值回复。
根据dS=μSdt+σSdz,假定其他因素不变时,当期望收益率μ上升时,股价S也会有上升的趋势。为了简化起见,我们先不考虑股票价格的波动率,即我们先假设股票价格的波动率为0的极端情况:
由dS=μSdt+σSdz和σ=0,我们可得dS= μSdt。两边同时除以S,得=μdt。在0~T的时间段内求积分,即可得。两边除以S0,结果为

由(1)可知,当S0给定时,μ的上升会使ST也随之上升。但是,当一个公司走过其成熟期而进入到衰退期时,此时公司的经营风险将会随着经营时间的延长而不断增长,盈利会减少,成长性的投资机会(PVGO)会趋于零,此时投资者会要求一个较高的预期回报率(这是因为这时的公司对系统性风险的反应灵敏度增加,对系统性风险的抵抗力下降所致),来弥补其所承担的风险,因此公司的价值也会跟着减少,股价下跌。这就出现了矛盾,根据,μ上升,eμT会跟着上升,0也上升,即预示着未来股价会比现时股价更高。但随着衰退期的持续,公司只会越来越亏损,其价值只会不断减少,直至最后资不抵债而完全退出市场或被其他公司兼并。所以,dS=μSdt+ σSdz中假定漂移率μ恒定是存在局限性的,一旦将μ内生化我们就会发现股价比并不是以恒定不变的期望收益率μ增长的,而是由股票的内在价值决定的。因此,更确切地说,我们需要改变以往的观点,以“回复”的新观点重新看待股票价格的波动问题。
三、股票价格的价值回复理论
根据公司金融理论可知,股票的价格由其所代表的公司的每股价值(公司的价值=公司的权益价值+公司的负责价值,即V=E+L,每股价值决定的。
由价值可加性原理和价值守恒定律,我们知道一个公司的价值应等于其所投资的各个投资项目的未来期望现金流现值的总和。
因此,可以得出一个公司的价值在第0期应等于
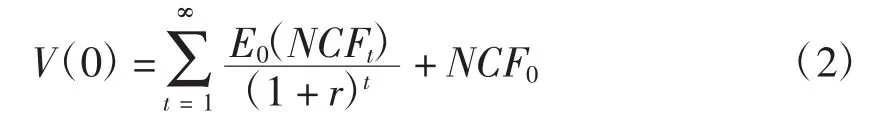
其中,E0(NCFt)为投资者在第0期对第t期公司的净现金流的期望值。而第t期的期望现金流净现值应为投资者在第0期对第t期公司投资的m个项目的期望现金流的净现值之和,即

这里的第0期只是一个记号,并不一定是指公司刚成立的时期。
同样,在第1期时该公司的价值可以用下式表示:

以此类推,在第n期时我们有

我们知道,股票的价格由于受到供求双方对未来股票价值不同预期的共同影响而围绕其价值上下波动。当股票价格偏离其价值时,在有效市场上由于套利活动的进行,其价格会不断地向其价值回复。且当市场均衡时我们有VP(t)=S(t)。因此,股票价格的变动可以用下式重新表示为:

其中,VP(t)是第t期股票的每股价值,VP(t)=假设公司不发行优先股)。
σ是股票价格的波动率,它是服从几何布朗运动的。研究表明,σ也存在均值回复的现象,可以用EWMA(不考虑其均值回复现象)或GARCH(p,q)(考虑其均值回复现象)等方法回归得到。但是,有证据表明股票的价格与其波动率呈负相关关系。Rubinstein[14,15],Jackwerth和Rubinstein[16]研究过权益性期权的波动率微笑问题,发现其波动率会出现倾斜情况(volatility skew)。
为了进一步研究股票价格的均值回复现象,我们假设a为股票价格向其价值回复的速率,即当VP(t)≠S时,股价以a的速度向VP(t)回复。因此,一国的证券市场越有效,证券价格一旦偏离其内在价值时应该以更快的速度向其内在价值回复,即a应是E的函数,记为a(E),这里E为证券市场有效性指标。证券市场越有效,E的取值应该越大。因此,a(E)越大,则证券市场越有效。所以a′(E)>0。
一个公司的盈利能力决定了一个公司的股东可以从公司获得回报的多少,同时也决定了其股票的内在价值。由于存在规模报酬效应和受边际报酬递减规律的制约,一个公司的价值不可能趋向于∞,公司经过一个高速增长期之后,必然会进入一个相对稳定的增长期,并最终步入衰退期。因此,一个公司的价值增长轨迹可以由图1表示:
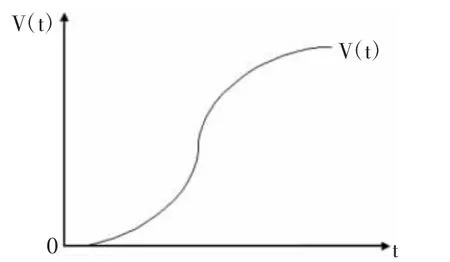
图1 公司总价值V(t)的时间增长趋势图
假设公司不增发股票,且不付红利(无此假设也不影响下文结论)。例如当一个公司流通中的普通股股份↑→VP(t)↓,继而S↓。虽然股票价格的波动依然遵循几何布朗运动,但是当S>VP(t)时,股票的价格有下降的趋势;当S 图2 股票价格的价值回复现象注:图中的大括号为正态分布概率密度函数,下同。 在传统金融经济学研究股票定价问题时所采用的dS=μSdt+σSdz中,我们假定股票价格的波动服从几何布朗运动,且期望收益率μ是恒定不变的。图3所示的是当μ恒定不变时,股票价格随时间增长的变化趋势。根据,μ上升,eμT也会跟着上升,继而也上升,即未来股价将会比现时的股价还要高。但是公司一旦进入衰退期,其经营只会越来越亏损,期望的现金流量会大幅缩水,公司的内在价值也会减少,以至最后完全退出市场。所以,这种恒定不变的漂移率是值得商榷的。因此我们将期望收益率进行内生化。将期望收益率内生化可以使我们得出μ与现实更符合的一些新结论。 图3 μ恒定不变,股票价格随时间增长的趋势图 我们知道,股东对公司要求的期望回报率应该与该公司面临的其所不能分散的系统性风险正相关。回顾公司成长的历程,在公司起步并进入成长期时,此时的公司对系统性风险的反应灵敏度较大,股东对公司要求的回报率也应该较高。相反,当公司进入成熟期后,经营稳定,风险也较小,股东此时的期望回报率也应相应减少。当公司进入衰退期后,由于风险的加大,此时投资者会要求一个较高的预期回报率来弥补其所承担的风险,因此公司的价值也会跟着减少,从而引起股价的下跌,见图4。 图4 每股价值与股东对公司要求的期望回报率趋势图 由于V(t)与VP(t)呈正比例关系,因此V(t)也可以用VP(t)代替。由此,VP(t)↑→μ↓,且μ始终大于rf。但现实中的μ不仅受公司所处生命周期阶段的影响,也受宏观经济状况(或市场组合期望收益率rm)变动的影响。 现代宏观经济学认为,经济的运行并不存在任何规律性或周期性的形式。不同类型和大小的扰动,以随机的方式影响实体经济,产出的增长大致对称地围绕其均值分布,经济周期并不存在(Romer[17])。 假设一个社会的生产函数可由柯布道格拉斯生产函数表示: 其中0<α<1,0<β<1,At=λAt-1+εt,0<λ<1。εt是一个随机扰动项,它以随机的方式来影响全要素生产率A。因此,我们可知Yt是一个维纳过程。如果证券市场是完美市场(perfect market),即证券市场上的信息是充分且对称的,则任何的总供给冲击或外生的技术冲击必然会以最快的速度在证券价格上表现出来。由于产出的变化是随机扰动的,因此证券市场的价格也应是随机扰动的,即证券价格的变动遵循随机游走过程,故证券市场的期望收益率rm也应遵循随机游走过程。但是证券市场的价格并不是机械地随着Yt的变动而变动,其反应的是整个系统性风险的变动。因此,其它系统性风险中组成要素的变动(如总需求冲击、未预期到的财政货币政策干预等)也会引起证券市场价格的变动,见图5。 图5 每股价值与ε(rm)变动的情况 假设rm以函数ε(rm)的方式影响0,则我们可以把每股价值表示为下式: 其中Fu<0,Fε>0,εrm<0 令Eε(rm)=0,Var[ε(rm)]=σ2,当市场效率不变时,我们有 因此,我们可以得到a(E)·ε(rm)的维纳过程表达式: 由于证券市场的价格并不是机械地随着Yt的变动而变动,而是反映整个系统性风险的变动,因此,证券市场的价格有时会与Yt的变动不同步,甚至相背离,即出现证券市场价格指数涨跌幅度与GDP不同步的现象。 由以上的分析可知,图2可修正为图6。 图6 股票价格的修正价值回复现象 此外在有效市场上上市公司的价值也是随机游走的。根据金融经济学和公司理财学的基本观点,我们知道公司的价值是由其所发放的股利的现值总和决定的。 设V(t)为在第t期时公司的价值,Dt为第t期公司发放的股利总和,Bt为第t期时公司已有的净现金流量,Et(NCFt+s)为在第t期预期的第t+ s期公司的净现金流量,Et+1(NCFt+s)为在第t+1期预期的第t+s期公司的净现金流量,r为公司的WACC,且假定为常数。 则公司在第t期时公司的价值为 且 故,公司在第t+1期时的价值可以表示为 根据上面的推导和理性预期理论的观点,我们可以看出在任何一个时点上,金融市场的参与者都会根据现在对未来公司净现金流量的无偏估计来预期他们所投资的公司的价值。随着时间的推移,他们改变对公司价值的预期仅仅是因为他们得到了使他们修正其预期的信息。 如果金融市场的参与者都是具有理性预期的投资者,那么 由(13)可知,在第t+1期,公司的价值是由金融市场的参与者在第t期对公司在第t+1期及以后各期股利发放预期的基础上,加上在第t+1期对公司在本期及以后各期净现金流量的预期与在第t期对公司在第t+1期及以后各期净现金流量的预期的差共同决定的。由于在第t+1期是不变的,因此,公司的价值从V(t)到V(t+1)的变动是由基于理性预期的投资者所获得的第t+1期的新信息和利用这些新消息所做出的关于公司价值最优预期的变化引起的。即由于金融市场的参与者只对完全未预期到的信息作出反应,因此,公司价值的变动也是无法预期的。只有金融市场上未被预期到的信息才会引起市场参与者修正其对公司价值的判断。这也进一步证明了在有效市场上反映公司价值的股票价格也应该是随机游走的。 股票价格的波动服从几何布朗运动是现代金融学常用的经典假设之一。正因为股票价格的波动是Markov过程,因此股票价格彼此之间是不相关的。传统的金融学理论把股票价格的波动表示为dS=μSdt+σSdz。本文正是在这基础上进行了新的修正,从而建立了股票价格波动的新理论模型,即价值回复模型,力图使股价的波动有一个更完整的理论基础。 本文研究分析的价值回复模型也可应用于股权类金融衍生产品的定价、B-S微分方程的修正及外汇的均衡汇率回复现象的研究等领域。 [1]Cootner,P.,1964,“TheRandom CharacterofStock Market Prices”[M].Cambridge,Mass:MIT Press. [2]Fama,and Eugene F.,“The Behavior of Stock Market Prices”[J].The JournalofBusiness(Chicago,Ill.),1965,38(1):34-105. [3]Black F.,and M.Scholes,“The Pricing of Options and Corporate Liabilities”[J].Journal of Political Economy,1973,81(3):637-659. [4]Richardson M.,and T.Smith,“A Test for Multivariate Normality in Stock Returns”[J].Journal of Business(Chicago,Ill.),1993,66(2):295-321. [5]Trabelsi,A.,and Oueslati,A.,“The Dynamics of Stock Price Adjustments to New Information:Empirical Evidence from the Tunisian Stock Exchange Market”[J]. Finance,2004,18(2):23-52. [6]Vagnani,G.,“The Black-Scholes Model As A Determinant of the Implied Volatility Smile:A Simulation Study,”[J].Journal of Economic Behavior&Organization,2009,72(1):103-118. [7]翟爱梅,王雪峰,冯英浚.股票价格的塑性理论模型[J].哈尔滨工业大学学报,2005(9):1277-1279. [8]赵巍,何建敏.股票价格遵循分数Ornstein-Uhlenback过程的期权定价模型[J].中国管理科学,2007(3):1-5. [9]余文利,廖建平,马文龙.一种新的基于隐马尔可夫模型的股票价格时间序列预测方法[J].计算机应用与软件,2010(6):186-189. [10]林勇,郭林军.有效市场假设与分形市场假设[J].预测,2002(2):34-38. [11]范申,王晓天,文志雄.重分式Poisson过程——一个新的股票价格运动模型[J].武汉大学学报:理学版,2005(1):15-19. [12]顾钰.我国股票市场价格波动与成交量关系的实证分析[J].现代商业,2010(32):36. [13]马永亮,叶昕,姜国华.价格波动性与股票预期回报——基于中国市场的初步证据[J].上海立信会计学院学报,2011(1):57-66. [14]Rubinstein M.,“Non-parametric Teats of Alternative Option Pricing Models Using All Reported Trades and Quotes on the 30 Most Active CBOE Option Classes from August 23,1976,through August 31,1978”[J].Journal of Finance,1985,40(2):455-480. [15]Rubinstein M.,“Implied Binomial Trees,”[J].Journal of Finance,1994,49(3):771-818. [16]Jackwerth J.C.,and M.Rubinstein,“Recovering Probability Distributions from Option Prices,”[J].Journal of Finance,1996,51(5):1611-1631. [17]Romer,D.“Advanced Macroeconomics”[M].McGraw-Hill Education,4th Edition,2011.
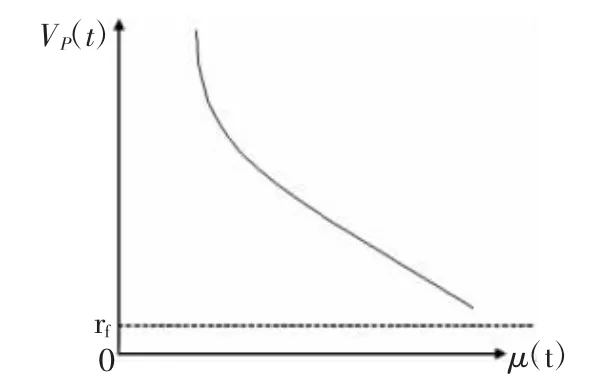
四、期望收益率μ内生化和上市公司的价值波动