甲板开口围缘扁钢加强方式研究

李霞丽，张世联，李敏

上海交通大学船舶海洋与建筑工程学院，上海 200204

0 引 言

因总体布置需要，甲板通常具有较大的矩形开口。而开口容易破坏结构的连续性，使甲板变成间断构件，致使甲板剖面上的应力重新分配，特别是在开口角隅处，会引起应力的高度集中，因而是船舶设计者十分关注的问题。为降低开口处的应力集中，通常采取的措施有：增加开口角隅板厚或贴板加强［1-2］、增大角隅圆弧半径［3-4］或改善角隅形状［5-10］，以及加设围缘扁钢［11-12］等。对于前两种措施，已有较多文章探讨过，而对围缘扁钢加强方式的研究则相对较少，尤其是在甲板大开口但没有使用甲板端梁的情况下，围缘扁钢的尺寸参数对加强效果的影响明显。本文将采用有限元法研究不同甲板尺寸和角隅半径时，扁钢尺寸参数的变化对开口处应力集中的影响，并基于最小应力集中系数（SCF）和最小结构重量的原则，进行开口处围缘扁钢加强方式的优化设计。

1 甲板开口模型

本文以某船主甲板上一矩形开口为研究对象，根据对称性取半宽模型，沿船长方向取一个舱段范围，甲板尺寸为24.8 m×15.3 m。考虑到在总纵弯曲作用下甲板受到的主要是面内载荷作用，此时，加强筋主要提供承载面积；而且通过对比同样板厚情况下有甲板骨材和没有甲板骨材两种甲板开口受外力作用后的应力分布及应力集中效应，发现热点应力集中在甲板骨材之间的甲板开口角隅边缘上，骨材对应力集中的影响比较小；因此，将甲板上的骨材等效为板厚。等效后，甲板厚度td=14 mm，开口位于距中纵剖面6 m位置处，尺寸为2a×2b=7.7 m×2.7 m，开口角隅处采用圆弧过渡，半径r=300 mm。甲板的材料为Q235钢，弹性模量E=206 GPa，泊松比 μ=0.3。有限元计算模型如图1所示，模型中横剖面约束x和z向位移，中纵剖面处约束y和z向位移。模型两端施加σ0=120 MPa的拉应力。甲板采用四边形壳单元模拟，对开口周围网格进行局部细化，尺寸为50 mm×50 mm，外围区域网格尺寸为800 mm×800 mm。

2 未加强时的计算结果

根据计算，甲板开口未加强时的应力分布如图2所示，其分布特点是：短边上受压，应力较小；长边上受拉，应力较大，并逐渐向外递减；4个开口角隅处会产生较大的应力集中，最大应力位置为圆弧与长边的相切点。Von Mises应力最大值σmax=369 MPa，取甲板上远离开口处的平均拉应力σ0为基准应力，则应力集中系数为

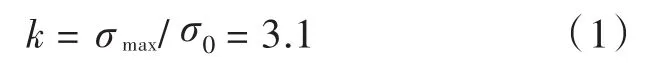
3 全范围围缘扁钢加强

当外载荷以及开口尺寸一定时，对开口全范围采用围缘扁钢加强。开口处的应力值主要与甲板的厚度td、扁钢的宽度br及厚度tr相关，可将开口处的应力集中系数表达为

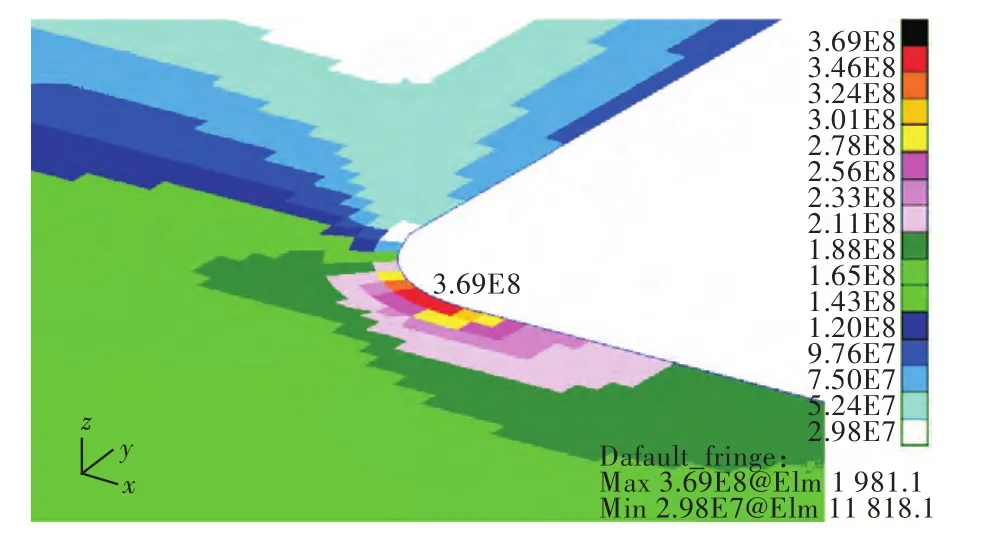
图2 未加强时开口角隅处应力分布Fig.2 Stress distribution on deck around the opening corners without reinforcement

可将围缘扁钢的应力集中系数k定义为最大应力与甲板平均应力进行无量纲化作为其应力集中的度量，以便与甲板上的应力集中系数做横向比较。

所谓全范围加强，即绕开口内缘贴一整圈扁钢取br=100～500 mm，每隔100 mm计算一个模型；取tr=10～30 mm，每隔1 mm计算一个模型。扁钢单元大小取为50 mm×50 mm，研究开口处应力集中系数k随br和tr变化的规律。

围缘扁钢加强时开口角隅处的应力分布如图3所示。短边上应力较小，长边上应力较大，远离角隅处的应力值逐渐减小；开口4个角隅仍出现较大的应力集中，但全局应力最大值的位置发生了变化，出现在了圆弧边缘靠近转角点处。

图3 围缘扁钢加强时开口角隅处应力分布Fig.3 Stress distribution on deck around the opening corners attached ring plate

上述现象的原因可以通过其受力进行分析。围缘扁钢加强时，由于扁钢对于甲板开口周围的变形产生了约束，开口相连处除了沿开口的周向应力之外，还会产生较大的径向应力，从而由单向应力状态变为双向应力状态［12］。此时，最大应力不再只出现在最大周向应力位置，而是在周向应力与径向应力共同形成的最大相当应力位置点，此位置偏离圆弧与长边的切点处，更靠近转角点，其具体位置与甲板和扁钢的刚度相关。

3.1 扁钢厚度、宽度的影响

在开口处采用围缘扁钢加强，应依据使开口区域应力集中系数k最小的原则确定最适宜的扁钢尺寸（tr-opt，br-opt）。

在td和br一定时，甲板和扁钢上的应力集中系数k随扁钢厚度比tr/td的变化趋势如图4所示，随着tr的增加，围缘扁钢上的k逐渐减小，甲板上的k则是先减小后增大；开口区域的k先减小后增大，最大应力位置由甲板过渡到扁钢上，k在tr/td=1.43，即tr-opt=20 mm时最小，kmin=2.16，应力集中水平降低约30%。

td一定时，不同扁钢宽度br下开口处的应力集中系数k随tr/td的变化趋势如图5所示，br越大，k越大；最佳tr-opt随br的增加而逐渐减小。

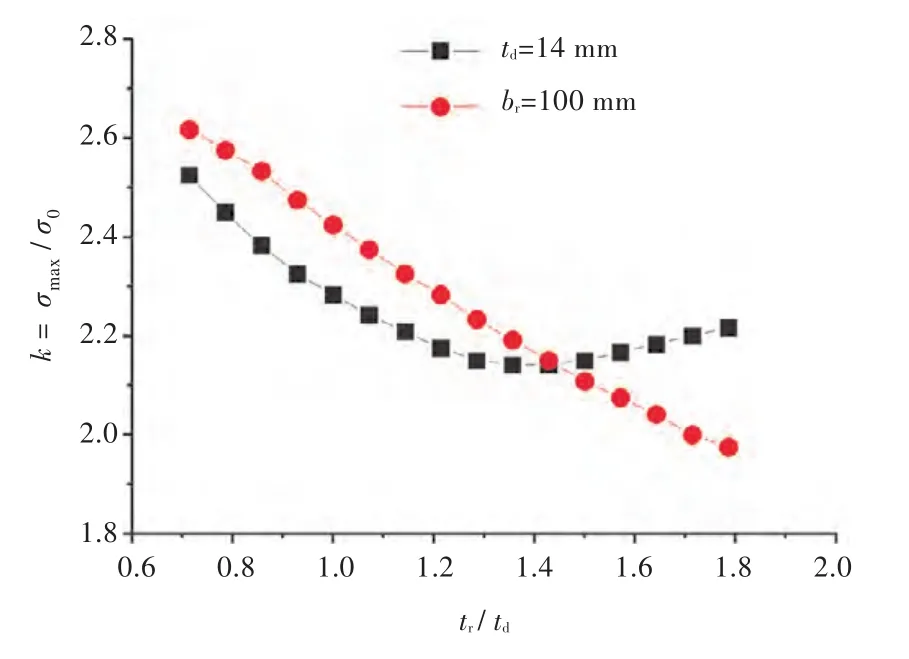
图4 甲板及围缘扁钢上应力集中系数k随tr/td的变化曲线Fig.4 Stress concentration factor（SCF）k on deck and ring plate versus tr/td

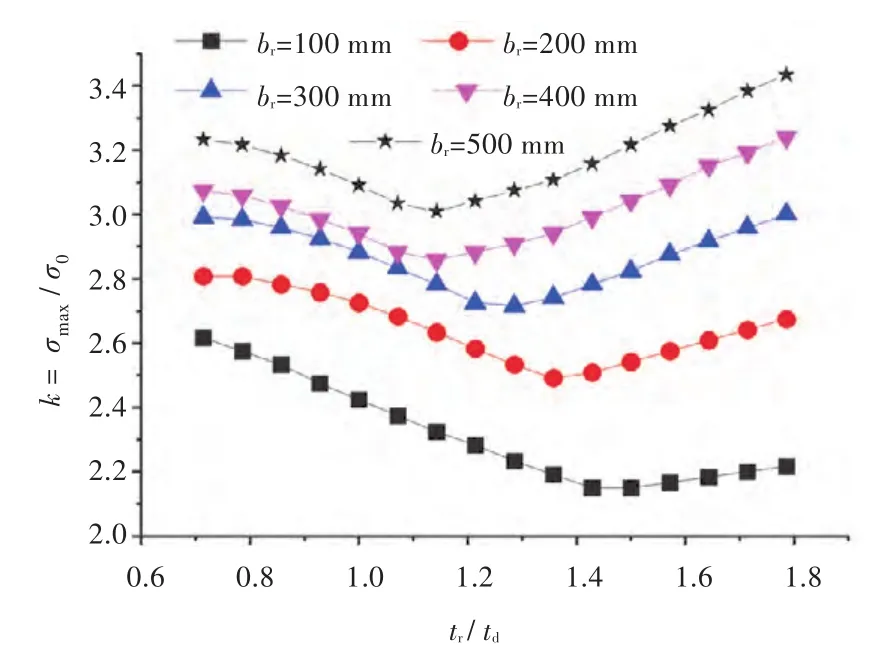
图5 不同br时开口处k随tr/td的变化曲线Fig.5 SCF k versus tr/tdwith br=100～500 mm

不同td和tr下，开口处k值随br变化的趋势如图6所示。可以看出最佳br-opt受tr和td影响不大，均在br-opt=100 mm时取得最小的应力集中系数。

图6 不同td和tr时，开口处k随br的变化曲线Fig.6 SCF k versus brwith different td，tr

从其受力变形进行分析，甲板受到面内拉应力作用时，角隅处的围缘扁钢变形如图7所示。扁钢在与甲板连接处随甲板一起发生了拉伸变形，上、下边缘为自由边，不受外力作用，相对于连接处便发生了受压作用的皱折现象。这种皱折变形在圆弧止端达到最大，使扁钢不能有效承担外载荷，扁钢及与其相连的甲板上应力分布发生变化，应力值大幅提高。

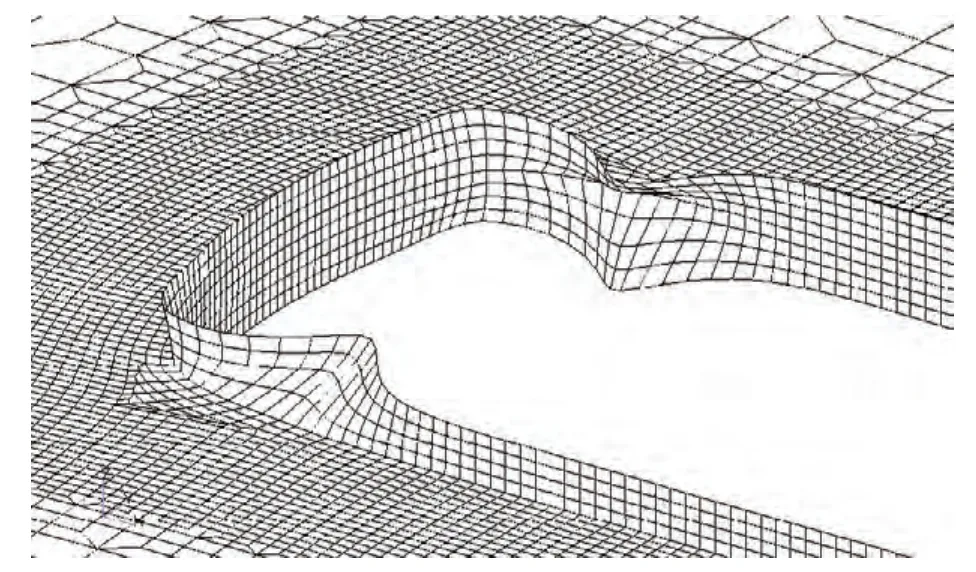
图7 开口处变形示意图Fig.7 Deformation around the opening corners

当tr/td超过一定数值后，扁钢越厚，刚性越强，甲板受到共同变形的牵引作用便越大，应力值反而增加。扁钢越宽，其柔性越大，皱折现象越严重，对应的应力值便越大，当宽度超过一定值后，不仅不能改善应力集中，反而会出现负效应，使得应力集中更显著（图6中虚线以上部分）。

由现有的经典结构力学知识可知，甲板开口的应力集中与r/a以及r/b数值相关［1］。本文保持角隅圆弧半径r不变，变换开口长宽a和b值，研究不同开口尺寸下，开口处应力集中系数k随扁钢宽度br的变化规律，如图8所示。由图8可以看出，应力集中系数均在br-opt=100 mm时达到最小，说明最佳扁钢宽度受开口尺寸的影响不大。通过进一步变换扁钢宽度值（在0～100 mm（间隔10 mm）之间），发现扁钢宽度在50～100 mm之间时应力集中系数最小，此时既不会产生明显的皱折增加应力值，又能减小应力集中。随着不同的开口尺寸变化，发现最佳扁钢宽度在50～100 mm之间变化，但应力集中变化不大，此时扁钢厚度是比较大的影响因素。实际应用中，可将br-opt=100 mm作为最佳扁钢宽度设计值。

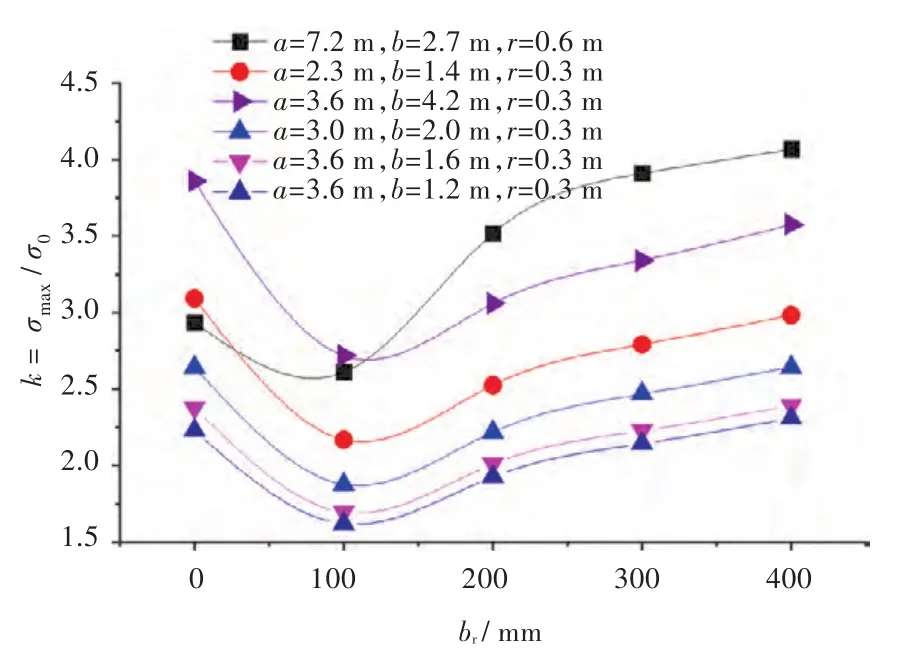
图8 不同开口尺寸时，开口处k随br的变化曲线Fig.8 SCF k versus brwith different opening sizes

3.2 扁钢宽度、厚度的优化设计

由第3.1节的分析可知，增加扁钢的宽度和厚度不一定能减小开口处的应力集中，应从最小应力集中系数出发对围缘扁钢进行优化设计，选取合适的扁钢尺寸，以便获得最佳的应力集中改善效果。

由文献［1］可知，当未加强时，甲板开口时影响应力集中系数的主要因素是角隅半径r与开口宽度b之比，r/b增大时应力集中系数急剧减小。扁钢最佳板厚是r/b和甲板板厚td的函数。

确定tr-opt的方法有图谱法和经验公式计算法。

变换角隅圆弧参数 r/b（0.14～0.5）时，开口处应力集中系数k关于td和tr的曲线图谱如图9所示。确定扁钢宽度后，根据甲板开口角隅圆弧参数r/b和甲板板厚td，再结合图谱便可以确定最佳扁钢厚度tr-opt，并可通过线性插值得到敷设该尺寸的围缘扁钢加强时能达到的最小应力集中系数。

此外，通过参数化分析发现，当r/b一定时，tr-opt与td基本呈线性关系，如图10所示。线性拟合可得到tr-opt计算式（3），式中，参数m和n查表1得出。在最佳扁钢厚度下，不同甲板厚度td时开口处的最小应力集中系数kmin随r/b的变化趋势如图11所示。可以看出，kmin基本不随td变化，仅由角隅圆弧参数r/b决定，随着r/b的增大，应力集中系数迅速降低。可以认为kmin是r/b的单值函数，其关系可由式（4）表达。

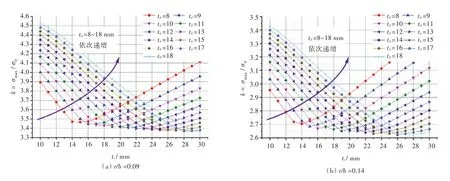
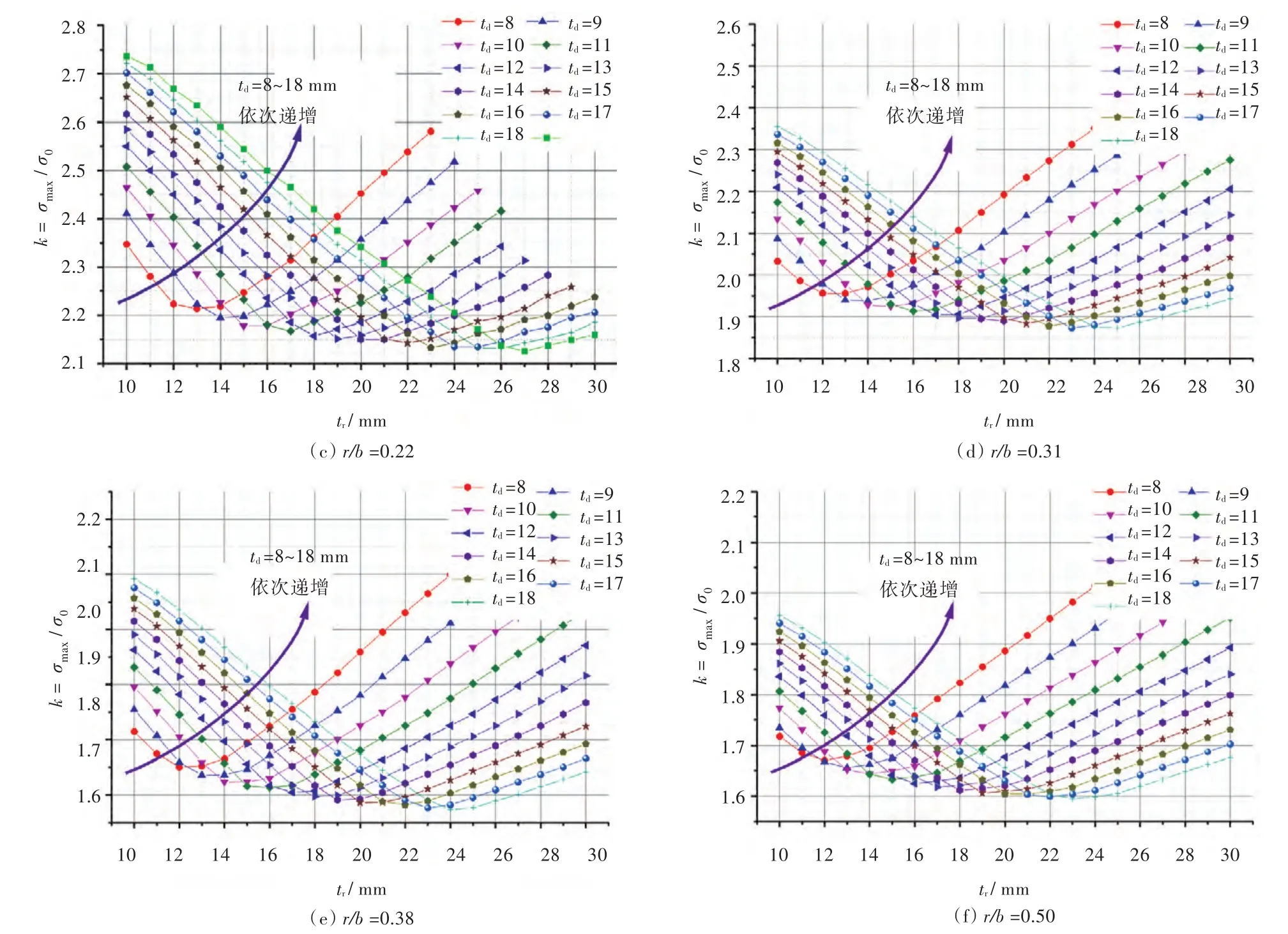
图9 不同角隅圆弧参数r/b下，开口处应力集中系数k关于td，tr图谱Fig.9 SCF k versus tr，tdwith different r/b

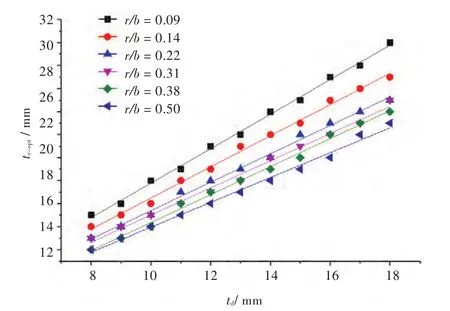
图10 不同r/b时tr-opt关于td的曲线图Fig.10 tr-optversus trwith different r/b

表1 不同r/b时的m和nTab.1 m，n with different r/b

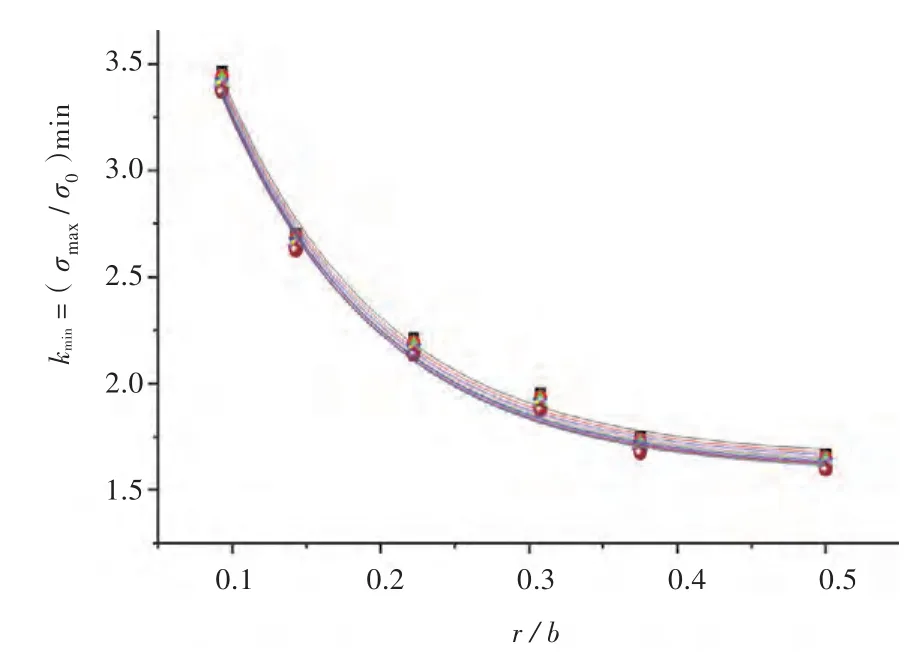
图11 不同td时开口处kmin关于r/b的变化曲线Fig.11 SCF k versus r/b with different td

3.3 实例验证

为验证式（3）和式（4）以及图谱的适用性，选取一块21.6 m×14.7 m的甲板，板厚为12 mm，甲板开口尺寸为2a×2b=4.5 m×1.4 m，角隅处圆弧半径r=300 mm，r/b=0.43，扁钢宽度为br-opt=100 mm，施加140 MPa的拉应力作用，进行计算分析。通过式（3）和式（4），计算得到扁钢板厚（m和n分别通过线性插值取得）以及对应的应力集中系数为：

围缘扁钢最佳板厚为16.6 mm，此时应力集中系数为1.66，即最大应力值为232 MPa，同样由图9（e）和图9（f）也可以估算出对应值。通过有限元数值计算，得到开口处最大应力值σmax和应力集中系数k随扁钢厚度tr的变化如表2所示。通过计算，得到tr=16 mm时应力集中系数最小，为1.71。最佳板厚和应力集中系数与提出的设计公式以及图谱所得值吻合较好，误差在3%左右。

表2 不同tr时开口处的k，σmaxTab.2 k，σmaxaround corner with different tr

4 局部围缘扁钢加强

由图2～图3的应力云图可以看出，不管是加强还是未加强时，都仅在开口角隅处出现了应力集中，在远离角隅的位置应力迅速衰减，扁钢加强效果较小。从节省钢料的角度出发，可以考虑只在应力集中的局部位置进行围缘扁钢加强的优化设计。

4.1 短边局部加强

甲板和开口尺寸不变，角隅圆弧和长边均增设围缘扁钢，扁钢尺寸取100 mm×20 mm，这是全范围加强的最佳扁钢尺寸。以开口角隅圆弧与短边切点为起点，在短边上依次取围缘扁钢长度lb=0～1 m，间隔0.1 m，计算甲板和围缘扁钢上的应力。开口局部加强时，在角隅处以及扁钢止端均有应力集中现象，最大应力值出现在角隅圆弧与长边连接相切处，应力集中系数随短边扁钢长度变化的趋势如图12所示。由图可知，随着开口短边上围缘扁钢长度的变化，开口处应力集中系数几乎不变。由此可以得出，短边上的围缘扁钢对改善角隅应力集中贡献比较小，可以根据实际结构设计和布置的需求，进而进行适当的截断处理，进行优化设计。

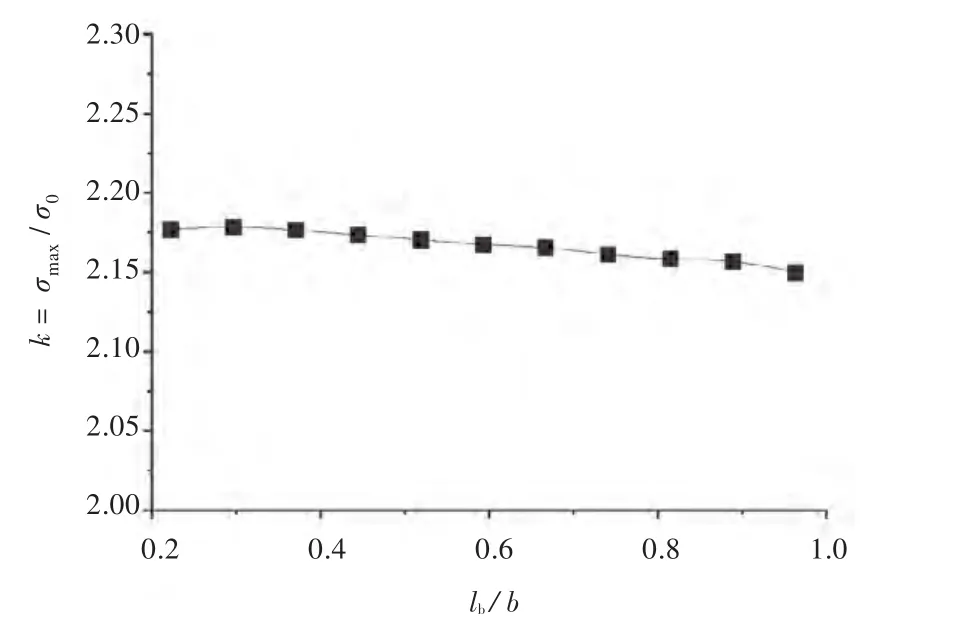
图12 开口处k随短边长度lb的变化曲线Fig.12 SCF k versus lb

4.2 长边局部加强

在同样的开口尺寸和甲板尺寸下，以开口角隅圆弧和长边切点为起点，在长边上取围缘扁钢长度la=0～3 m，间隔0.2 m，计算甲板和扁钢上的应力。开口区域的应力分布如图13所示，从中可见，在开口角隅处和和扁钢止端均出现了较大的应力集中现象。

图13 围缘扁钢长边局部加强时开口区域应力分布Fig.13 Stress distribution on deck around the opening with local reinforcement on the long side

开口区域和角隅处的应力集中系数k随la/a的变化趋势如图14所示。由图可见，长边局部加强时，随着扁钢长度的增加，开口角隅处k逐渐增大，扁钢止端k逐渐减小。

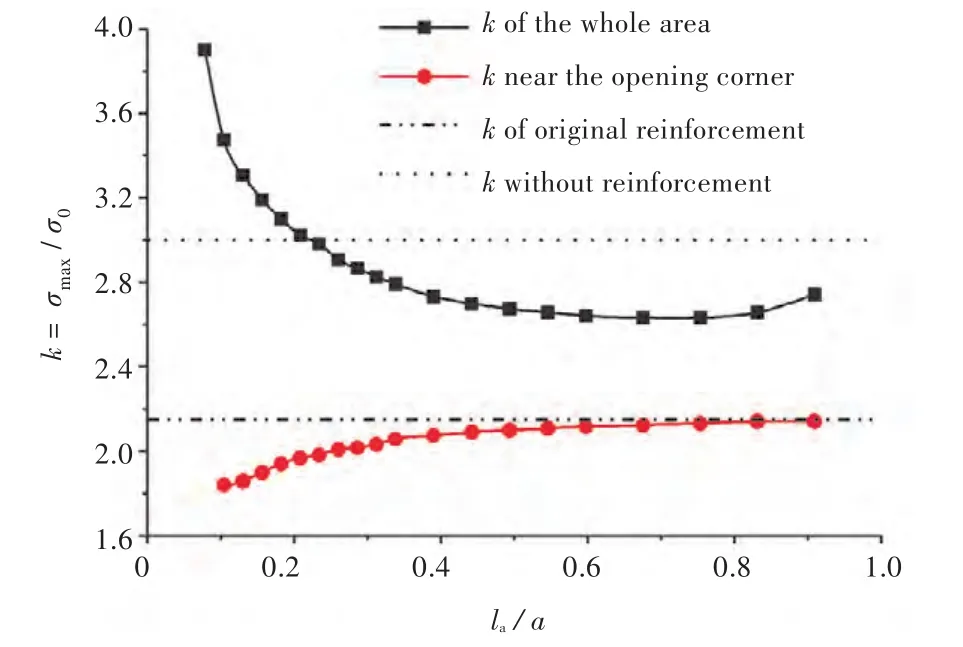
图14 开口角隅处和扁钢止端k随扁钢长度la/a变化曲线Fig.14 SCF k around the corner and at the end of the ring plate versus la/a

扁钢止端k始终大于开口角隅处的k值，说明最大应力值始终出现在扁钢长边止端与甲板相连处。当开口长边上扁钢长度较短，即扁钢止端接近角隅时，由角隅本身形状突变引起的应力集中和由围缘扁钢中断引起的应力集中叠加，会产生很大的应力；当围缘扁钢止端延伸至远离角隅处时，两种应力集中因素错开，分别在角隅处和扁钢止端产生应力集中，从而使得整体应力集中水平下降。

由以上分析可知，采用围缘扁钢进行局部加强时，应避免在开口的长边上断开。扁钢在长边上断开，形成的新的间断构件会产生附加的应力集中，不仅不能增强开口处的结构强度，反而会增加应力集中水平。在实际应用中，即使需要在长边上打断围缘扁钢，也应避免在开口角隅附近终止。适当地延长扁钢长度至开口长度的20%（图14中，la/a=20%时应力集中系数达到最小并趋于平稳），便能有效降低应力集中水平。

5 结 论

通过研究对不同尺寸的甲板及其矩形开口采用围缘扁钢加强时，扁钢尺寸参数对开口处应力集中的改善效果，得到以下结论：

1）通过敷设适当尺寸的围缘扁钢加强可以有效降低甲板开口角隅处的应力集中。

2）敷设扁钢使开口处的应力变为双向应力状态，扁钢尺寸并非越大越好，当宽度和厚度增加到一定数值后反而会造成更大的应力集中，应力集中系数随扁钢尺寸的增大是先减小后增大，需要从最小应力集中的角度出发对围缘扁钢进行合理设计。

3）扁钢的最佳宽度值通常在50～100 mm之间，最佳厚度是甲板厚度和角隅半径参数的函数，采用式（3）和式（4）或设计图谱，可以简便、快速地得到合理的扁钢厚度以及相应的应力集中系数。

4）从应力分析的角度来看，短边上的围缘扁钢对改善应力集中的贡献比较小，在实际结构布置允许的情况下，可以在圆弧切点处截止以优化设计。

5）围缘扁钢在长边上中断会产生较大的应力集中，应在全部长度范围上连续敷设。若因布置的需要需在长边上打断围缘扁钢时，也应避免在开口角隅附近终止。扁钢应延长至距离圆弧切点20%开口长度的位置以外，以避免产生过大的应力集中。

［1］杨代盛.船体强度与结构设计［M］.北京：国防工业出版社，1986.

［2］中国船级社.钢质海船入级与建造规范［S］.北京：人民交通出版社，2010.

［3］赵建华，吴剑国，俞铭华.舰船甲板大开口应力集中的理论分析［J］.华东船舶工业学院学报（自然科学版），1996，10（4）：15-19.ZHAO Jianhua，WU Jianguo，YU Minghua.Theoretical analysis of stress concentration in a large deck opening［J］.Journal of East China Shipbuilding Institute（Natural Science Edition），1996，10（4）：15-19.

［4］王林，吴剑国，俞铭华，等.船体甲板和侧壁大开口应力集中及其加强形式［J］.华东船舶工业学院学报（自然科学版），1998，12（3）：59-64.WANG Lin，WU Jianguo，YU Minghua，et al.Stress concentration of large opening in the deck and the sideboard of ship and its strengthening measures［J］.Journal of East China Shipbuilding Institute（Natural Science Edition），1998，12（3）：59-64.

［5］FRANCAVILLA A，RAMAKRISHNAN C V，ZIENKIEWICZ O C.Optimization of shape to minimize stress concentration［J］.The Journal of Strain Analysis for Engineering Design，1975，10（2）：63-70.

［6］KRISTENSEN E S，MADSEN N F.On the optimum shape of fillets in plates subjected to multiple in-plane loading cases［J］.International Journal for Numerical Methods in Engineering，1976，10（5）：1007-1019.

［7］王承先，陶政国.船舶甲板开口角隅形式的研究［J］.舰船科学技术，1984，（11）：10-14.

［8］俞铭华，徐昌文.船舶舱口角隅最佳形状的研究［J］.华东船舶工业学院学报（自然科学版），1988（4）：1-8.

［9］俞铭华，徐昌文.甲板矩形开口角隅形状优化设计和光弹性试验［J］.中国造船，1991（2）：45-55.

［10］蔡乾亚，杨永谦，裘泳铭.集装箱船舱口角隅的应力集中及其结构形式［J］.上海交通大学学报，1996（8）：125-129.

［11］吴家龙，何颖强，吴群益.纯弯梁加环孔边应力分析［J］.同济大学学报，1983（3）：83-95.

［12］夏志皋.加强孔口应力集中系数的合理定义［J］.上海力学，1990（1）：81-84.