基于PSO算法的船用永磁电机齿槽转矩优化

连军强，孙宏坤

1 海军驻桂林地区军事代表室，广西桂林 541000

2 海军驻黄埔造船有限公司军事代表室，广东广州 510715

0 引 言

随着舰船综合电力和稀土永磁技术的发展，永磁电机已被广泛应用于舰船推进领域。与传统的励磁电机相比，永磁电机具有低损耗、高功率密度等优点。然而，齿槽转矩作为永磁电机的固有特点会引起电机的振动、噪声和控制困难；因此，削弱永磁电机齿槽转矩成为永磁电机研究的重要方面。永磁电机齿槽转矩的产生来自永磁体与电枢齿之间的切向力，是永磁体与电枢齿槽相互作用的结果［1-3］，它受电机极弧系数、永磁体厚度、气隙长度、定子槽口宽度等多个设计参数的影响。这些设计参数与齿槽转矩之间呈现出既相互影响又相互制约的关系。所以在齿槽转矩参数优化时，需要在允许的参数空间内寻找一组最优的参数。采用有限元方法可以精确分析计算永磁电机的齿槽转矩，但该方法计算耗时长，且无法给出永磁电机设计参数与齿槽转矩之间的显性关系。本文拟提出一种基于粒子群算法的参数优化方法。该方法将建立齿槽转矩解析模型，并根据参数实际的取值范围确定约束条件，以齿槽转矩最小为目标函数，使用粒子群算法对该解析模型在设计约束的多维参数空间内进行参数寻优，从而得到最优的参数组合。

1 齿槽转矩解析模型及改进

目前，齿槽转矩的计算方法可以分为两类：解析方法和数值方法。其中，解析法的物理概念清晰。齿槽转矩的解析模型很多，主要分为基于能量法的齿槽转矩解析模型和基于麦克斯韦张量法的齿槽转矩解析模型两大类［4-7］。齿槽转矩参数优化对齿槽转矩解析模型有以下要求：

1）解析模型中要包含所有需要优化的设计参数，这样才能求得全局最优解；

2）解析模型要能精确计算齿槽转矩，且计算过程耗时要短，以减少粒子群寻优的时间。

由于基于能量法的齿槽转矩解析模型能直观地体现各设计参数与齿槽转矩的关系，且求解简单，所以选取基于能量法的解析模型，在参数选择时，取对齿槽转矩影响最大的极弧系数ap、永磁体厚度hm和定子槽口宽度b等参数为优化设计参数。齿槽转矩参数优化可描述为：

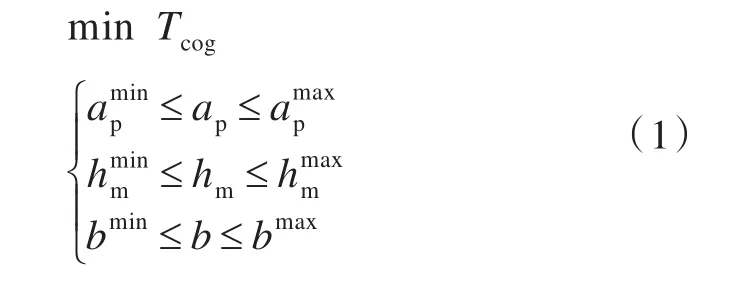
由于采用基于能量法的齿槽转矩解析模型，为便于计算，根据能量法［8］，齿槽转矩解析模型可进行以下化简：

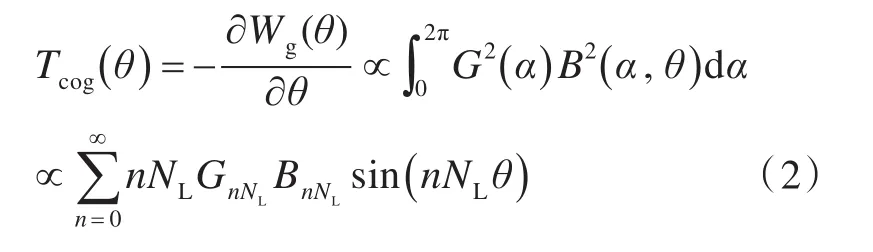
式中：θ为永磁体相对某一指定齿的中心线旋转的角度；Wg(θ)为电机在角 θ时的储能；G(α)为定转子相对机械角为α的气隙磁导；B(α，θ)为气隙磁密；NL为磁极数与定子齿数的最小公倍数；n=1，2，…，N ；GnNL为磁导的NL的整数次谐波；为磁密的NL的整数次谐波。

从上式可以看出，建立齿槽转矩解析模型的关键是推导出气隙相对磁导GnNL和气隙磁密BnNL的表达式，气隙相对磁导GnNL的表达式为

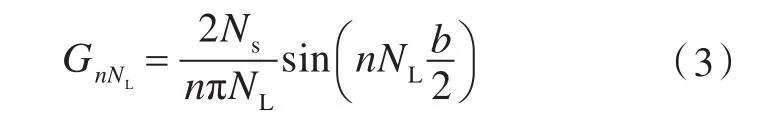
现对BnNL进行推导。在齿槽转矩模型中，一般都是将气隙磁密理想化为矩形，根据拉普拉斯和准泊松方程可得到精确的气隙磁密表达式［9-12］。本文选取径向充磁表贴式永磁电机为研究对象，在图1所示的表贴式永磁电机模型中，Rs为定子半径，Rr为转子铁心半径，Rm为转子外半径，永磁体厚度表示为：hm=Rm-Rr，气隙轴线的位置选在r==，对气隙磁密径向分量表达式进行变形，得

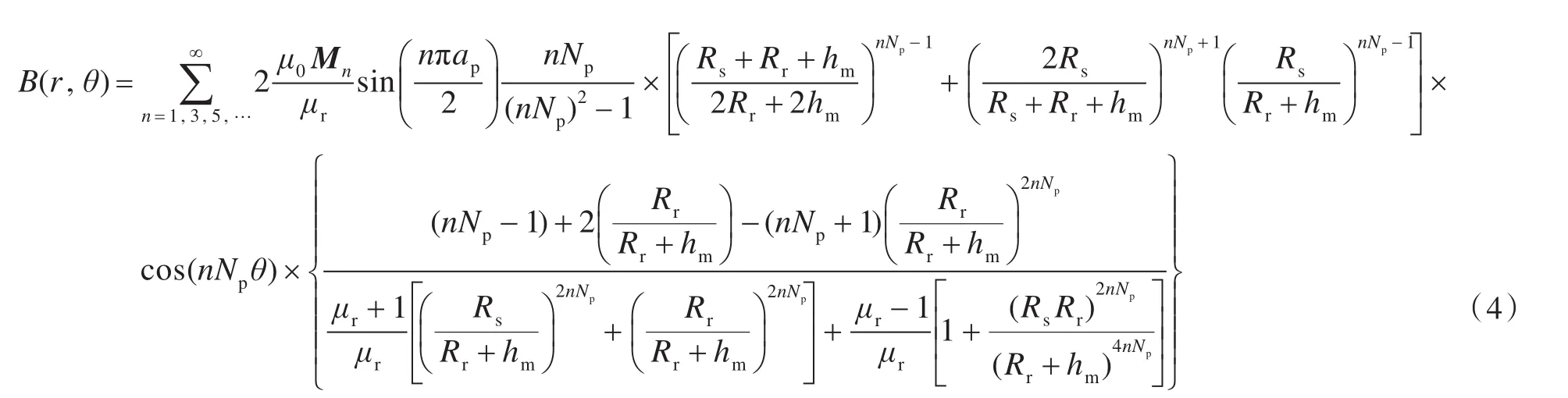
式中：Mn为磁化强度矢量；μ0为真空磁导率；μr为永磁体相对磁导率；Np为转子极对数。

在一个磁极范围内对式（4）积分，得

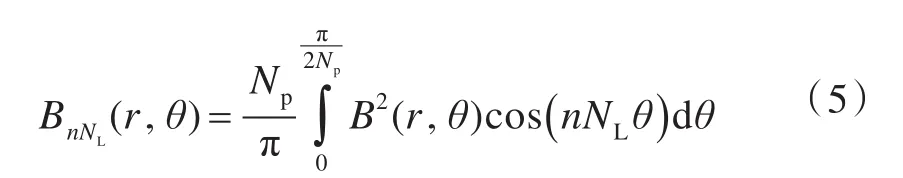
将式（5）和式（3）代入式（2），得到齿槽转矩的解析模型。解析模型中只有极弧系数ap、永磁体厚度hm和定子槽口宽度b为未知参数，其余均为已知量。

2 粒子群优化算法

粒子群算法（Particle Swarm Optimization，PSO）最早由Eberhart和Kennedy于1995年提出，基本概念源于对鸟群觅食行为的研究［13-15］。

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量：

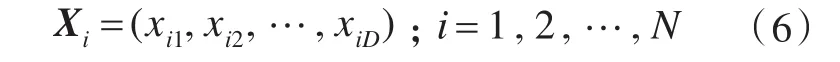
第i个粒子的“飞行”速度也是一个D维的向量，记为

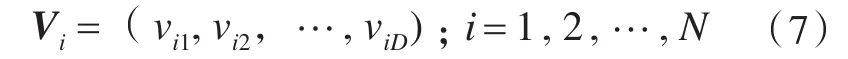
第i个粒子迄今为止搜索到的最优位置称为个体极值，记为

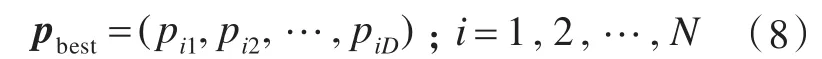
整个粒子群迄今为止搜索到的最优位置为全局极值，记为

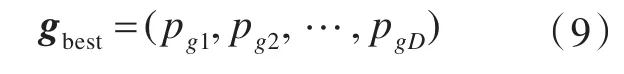
在找到这两个最优值时，粒子根据式（10）和式（11）来更新自己的速度和位置。

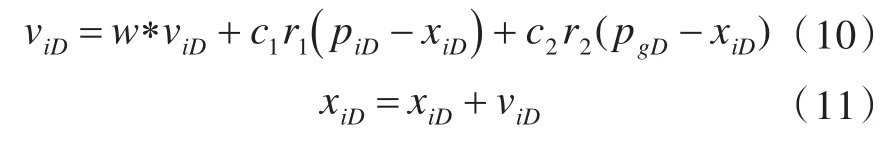
式中：c1和c2为学习因子，也称加速常数（acceleration constant）；r1和 r2为［0，1］范围内的均匀随机数［16］。算法流程如图2所示。

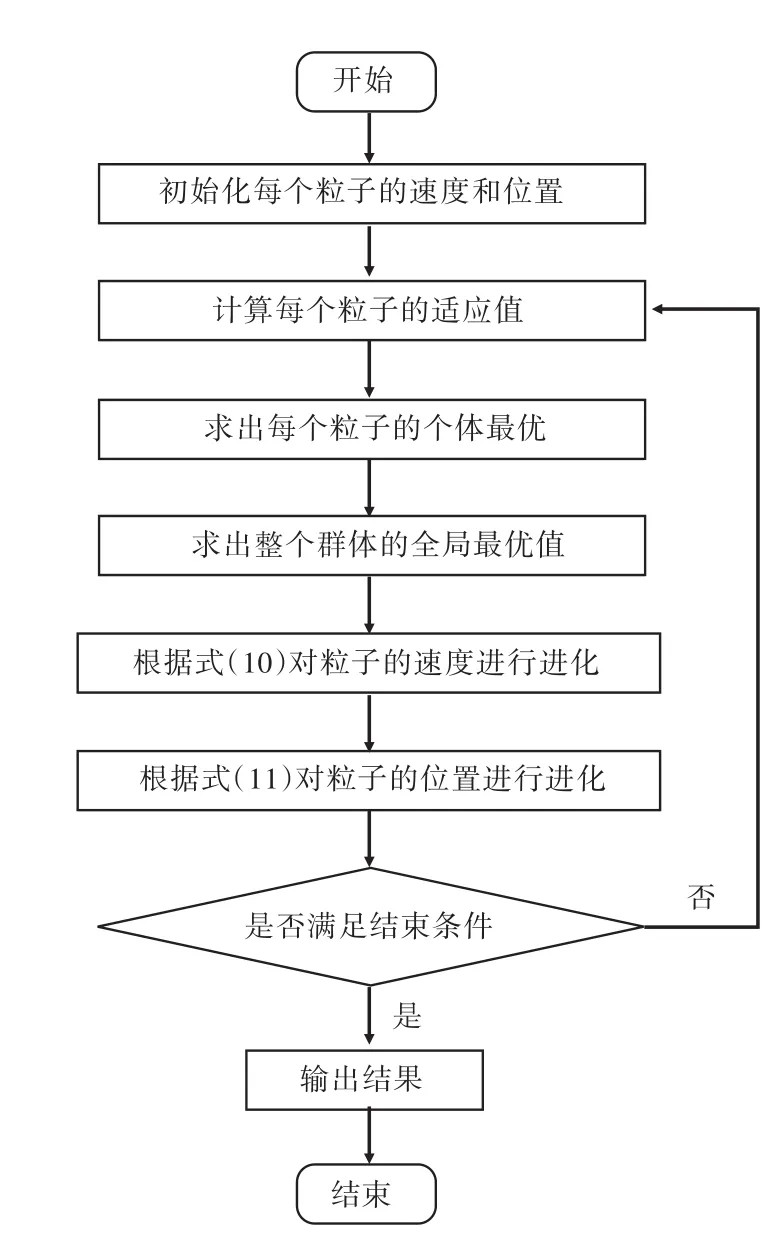
图2 PSO算法流程图Fig.2 The flow chart of PSO

3 齿槽转矩解析模型参数寻优及优化结果分析

以图1所示的表贴式永磁电机为研究对象，电机轴长94 mm，电机参数见表1。永磁电机极弧系数ap的取值范围[0 .6，0.9]，永磁体厚度hm（单位：mm）的取值范围[3 .5，6.5]，定子槽口宽度b（单位：mm）的取值范围[2 .25，2.75] ，解析模型中傅里叶级数迭代次数取20。将电机已知参数代入式（4）并进行化简，可得到电机径向磁场强度表达式：

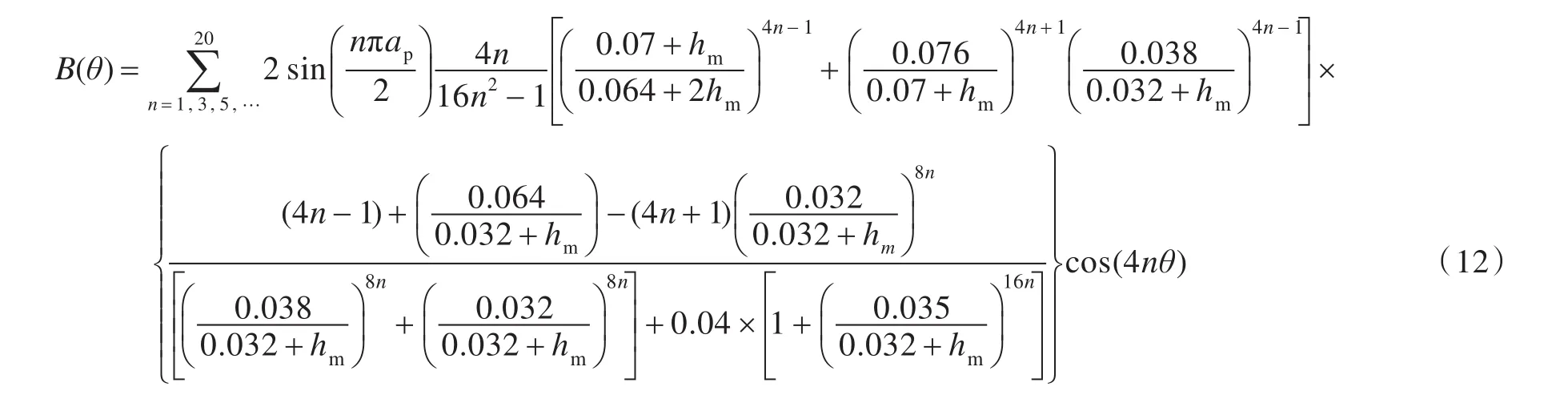
表1 电机参数Tab.1 Parameters of permanent magnet motor

由式（2）、式（3）、式（4）和式（12），可得到齿槽转矩的解析表达式

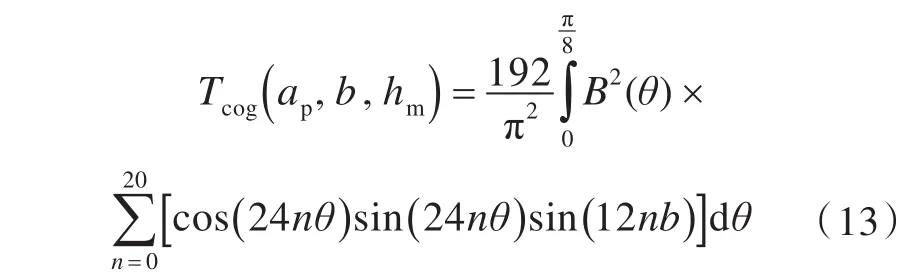
由式（13）所得的计算结果为沿气隙轴线分布的多个点的齿槽转矩值，而在电机设计过程中是将齿槽转矩的峰值作为性能指标，所以优化目标函数为

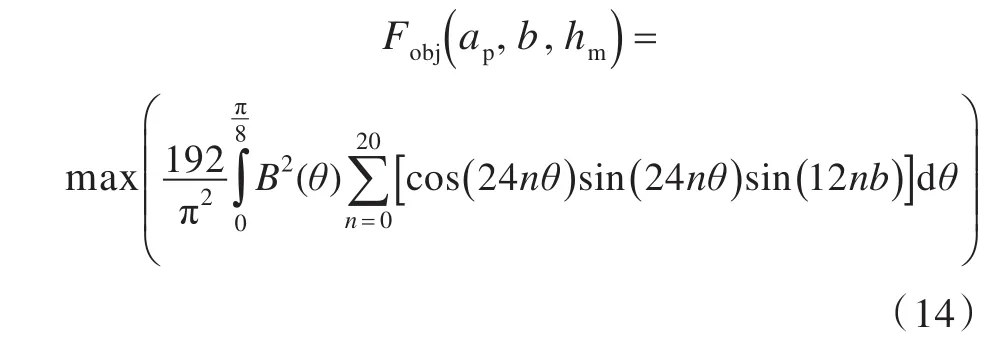
使用Matlab软件对齿槽转矩解析模型（式（14））进行编程，粒子群优化算法的参数选取为：种群数为50；最大迭代次数分别取50，100和200。图3所示为参数优化过程和优化函数收敛曲线。其中：图3（a）和图3（c）为迭代次数分别取50和200时，表贴式永磁电机3个对齿槽转矩影响较大的参数，即极弧系数ap、永磁体厚度hm和定子槽口宽度b在粒子群寻优过程中的变化；图3（b）和图3（d）为优化目标函数，即电机齿槽转矩峰值在迭代过程中的收敛曲线。迭代50次时，目标函数值为0.23 N·m；粒子群算法迭代100次时，目标函数值为0.13 N·m；粒子群算法迭代200次时，目标函数值仍为0.13 N·m；所以，粒子群算法在迭代100次已寻到全局最优值。

4 优化方法的有限元验证

Ansoft软件为专门的电机有限元计算软件，使用Ansoft软件自带的优化功能对文中所提出的优化算法进行验证，选择Optimetrics选项中的GA选项，即遗传算法优化选项，Ansoft软件中GA选项的数据样本是大量的有限元分析数据，因此优化结果可信，可作为本文所提出的优化算法的验证手段。GA选项的参数设置如图4所示，遗传算法寻优图和优化结果分别如图5和图6所示，迭代52次时取得全局最优值。

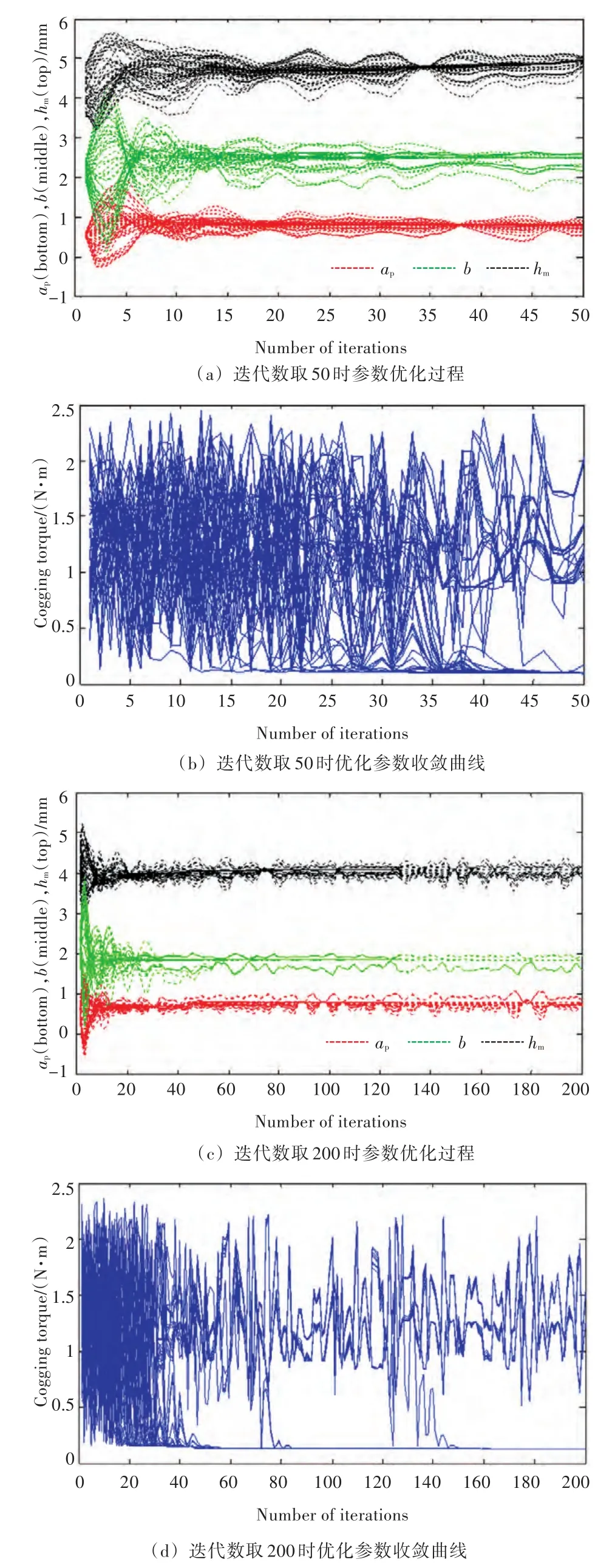
图3 参数优化过程和优化函数收敛曲线Fig.3 Progress of optimization of parameters and optimization function convergence

粒子群优化结果与Ansoft软件中GA选项优化结果的对比见表2。从中可见，粒子群优化后齿槽转矩值为0.13 N·m，遗传算法优化后齿槽转矩值为0.132 N·m，两者非常接近，但本文所提优化算法的优化时间要比Ansoft软件中GA选项优化时间少得多。这是由于基于粒子群算法的齿槽转矩优化方法是对齿槽转矩解析模型进行优化，它的样本数据由解析模型计算得到，而Ansoft软件中GA选项的样本数据是由有限元计算得到的，耗时较长。

图4 遗传算法参数设置Fig.4 The parameter setup of Genetic Algorithm

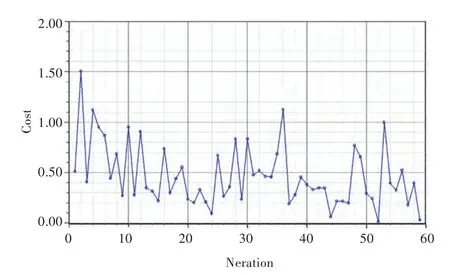
图5 遗传算法寻优图Fig.5 The progress of Genetic Algorithm search for optimistic result

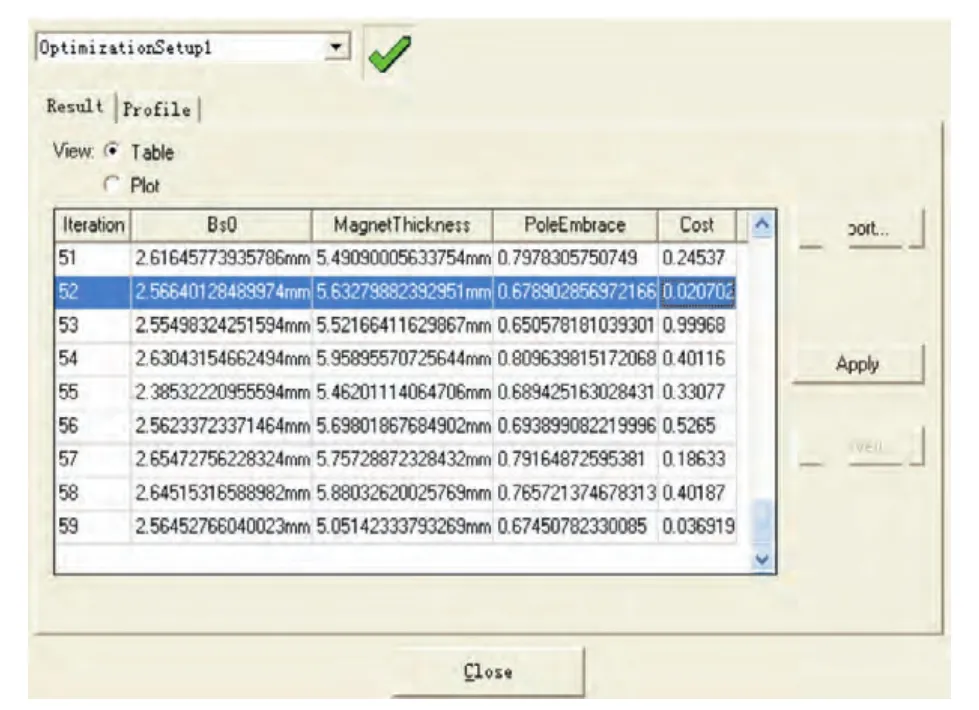
图6 遗传算法优化结果Fig.6 The optimization result by using Genetic Algorithm

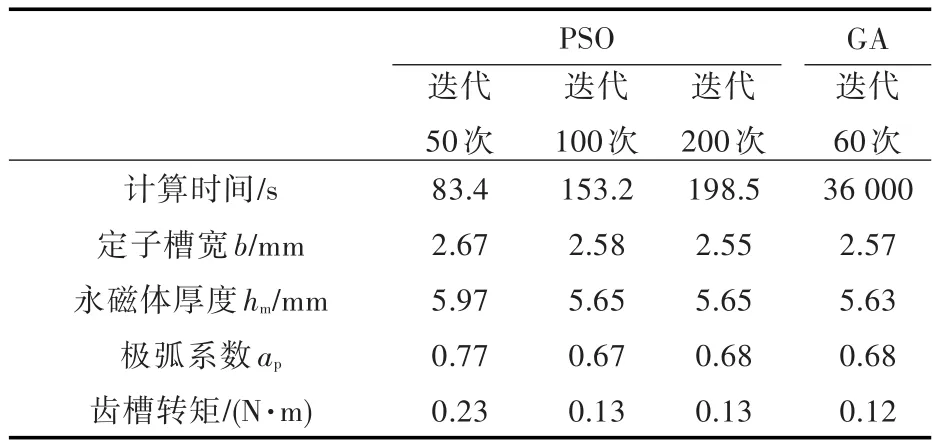
表2 优化结果对比Tab.2 Comparison of the optimization results

使用粒子群优化后的参数建立表贴式永磁电机的有限元模型，进行有限元分析，结果如图7所示。在进行仿真时，设置电机角速度为1（°）/s，故每秒对应机械度1°。电机参数优化前齿槽转矩值为1.23 N·m，使用粒子群算法对电机参数优化后，齿槽转矩值降为0.13 N·m，降低了近90%，说明基于粒子群算法的齿槽转矩优化方法能够有效对电机参数进行优化，达到大幅度削弱齿槽转矩的目的。

5 结语

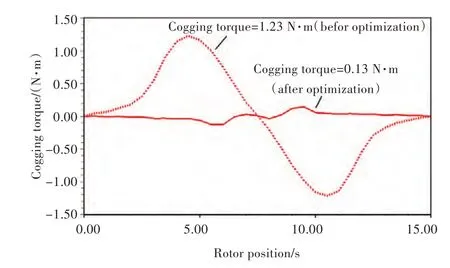
图7 PSO算法优化前后齿槽转矩对比图Fig.7 Cogging torque before optimization and after optimization

本文在对齿槽转矩解析模型进行变形和简化的基础上，选取对齿槽转矩影响较大的3个参数作为优化变量，以齿槽转矩峰值为优化目标量，使用粒子群算法进行优化，经有限元验证，该方法取得了较精确的优化参数，且计算时间大大缩短，说明基于粒子群算法的齿槽转矩优化方法能够有效对电机参数进行优化，达到大幅度削弱齿槽转矩的目的。

［1］SWANN S A.Effect of rotor eccentricity on the magnetic field in the air-gap of a non-salient-pole machine［J］.Proceedings of the Institution of Electrical Engineers，1963，110（5）：903-915.

［2］LORIMER W，HARTMAN A.Magnetically induced vibrations in brushless DC magnet motors［C］//28th Annual Symposium Proceedings of Incremental Motion Control Systems and Devices，1999：299-308.

［3］冀溥，王秀和，王道涵，等.转子静态偏心的表面永磁电机齿槽转矩研究［J］.中国电机工程学报，2004，24（9）：188-191.JI Pu，WANG Xiuhe，WANG Daohan，et al.Study of cogging torque in surface-mounted permanent magnet motors with static eccentricity［J］.Proceedings of the CSEE，2004，24（9）：188-191.

［4］张冉，王秀和，杨玉波，等.基于等效剩磁法的永磁电动机转子偏心磁场解析计算［J］.电工技术学报，2009，24（5）：7-12.ZHANG Ran，WANG Xiuhe，YANG Yubo，et al.Analytical prediction of magnetic field in permanent magnet motors with rotor eccentricity based on the method of equivalent remanence［J］.Transactions of China Electronics Society，2009，24（5）：7-12.

［5］HARTMAN A，LORIMER W.Undriven vibrations in brushless DC motors［J］.IEEE Transactions on Magnetics，2001，37（2）：789-792.

［6］章名涛，肖如鸿.电机的电磁场［M］.北京：机械工业出版社，1988：182-201.

［7］HWANG S M，KIM K T，JEONG W B，et al.Comparison of vibration sources between symmetric and asymmetric HDD spindle motors with rotor eccentricity［J］.IEEE Transactions on Industry Applications，2001，37（6）：1727-1731.

［8］KIM U，LIEU D K.Effects of magnetically induced vibration force in brushless permanent-magnet motors［J］.IEEE Transactions on Magnetics，2005，41（6）：2164-2172.

［9］LI J T，LIU Z J，NAY L H A.Effect of radial magnetic forces in permanent magnet motors with rotor eccentricity［J］.IEEE Transactions on Magnetics，2007，43（6）：2525-2527.

［10］NIAZI P，TOLIYAT H A.Online parameter estimation of permanent magnet assisted synchronous reluctance motor［J］.IEEE Transactions on Industry Applications，2007，43（2）：609-615.

［11］BURTH M，VÉLEZ-REYES G C.Subset selection for improved parameter estimation on on-line identification on a synchronous generator［J］.IEEE Transactions on Power Systems，1999，14（1）：218-225.

［12］程树康，宫海龙，柴凤，等.永磁轮毂电机齿槽转矩研究［J］.中国电机 工程学报，2009，29（30）：47-51.CHENG Shukang，GONG Hailong，CHAI Feng，et al.Study on cogging torque of permanent magnet in-wheel motor［J］.Proceedings of the CSEE，2009，29（30）：47-51.

［13］KATHIRAVAN R，GANGULI R.Strength design of composite beam using gradient and particle swarm optimization［J］.Composite Structures，2007，81（4）：471-479

［14］FAN S K S，ZAHARA E.A hybrid simplex search and particle swarm optimization for unconstrained optimization［J］.European Journal of Operational Research，2007，181（2）：527-548.

［15］DE FALCO I，DELLA C A，TARANTINO E.Facing classification problems with particle swarm optimization［J］.Applied Soft Computing，2007，7（3）：652-658.

［16］阮旻智，李庆民，王红军，等.人工免疫粒子群算法在系统可靠性优化中的应用［J］.控制理论与应用，2010，27（9）：1253-1258.RUAN Minzhi，LI Qingmin，WANG Hongjun，et al.Application of artificial immune particle swarm optimization algorithm to system-reliability optimization［J］.Control Theory and Application，2010，27（9）：1253-1258.