Stirling公式的进一步拓展

张丽颖

(健雄职业技术学院软件与服务外包学院，江苏太仓215411)

詹姆斯·斯特林(James Stirling)于1730年给出了:n!～C·n(n+12)·e－n，并求出了近些年，Stirling公式还多次被推广．其研究不断地深入．

1999年，徐利治［1］给出了n!的二重级数表达式并推出其双边不等式为

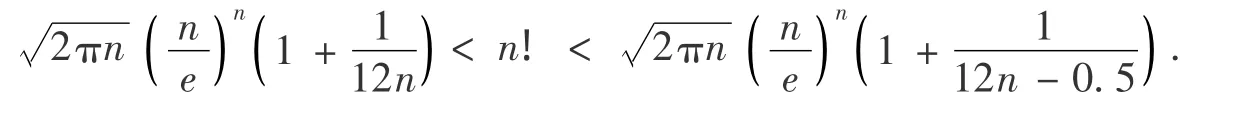
2004年，匡继昌［2］对Stirling公式做了进一步推演:

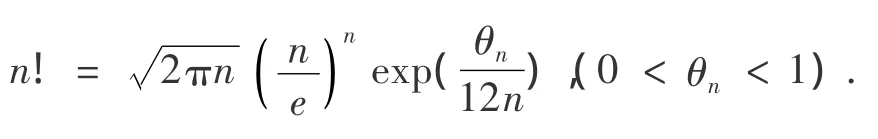
并指出，经常使用的n!近似估计式有:

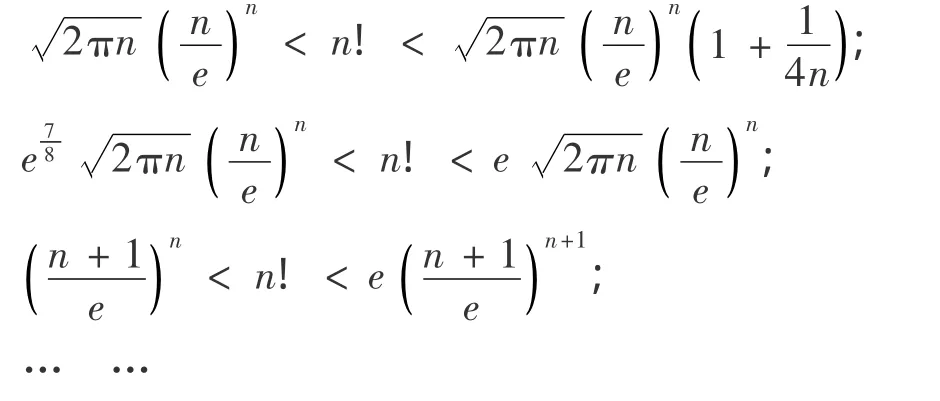
文献［3］、［5］、［6］也对 Stirling公式进行了论证:

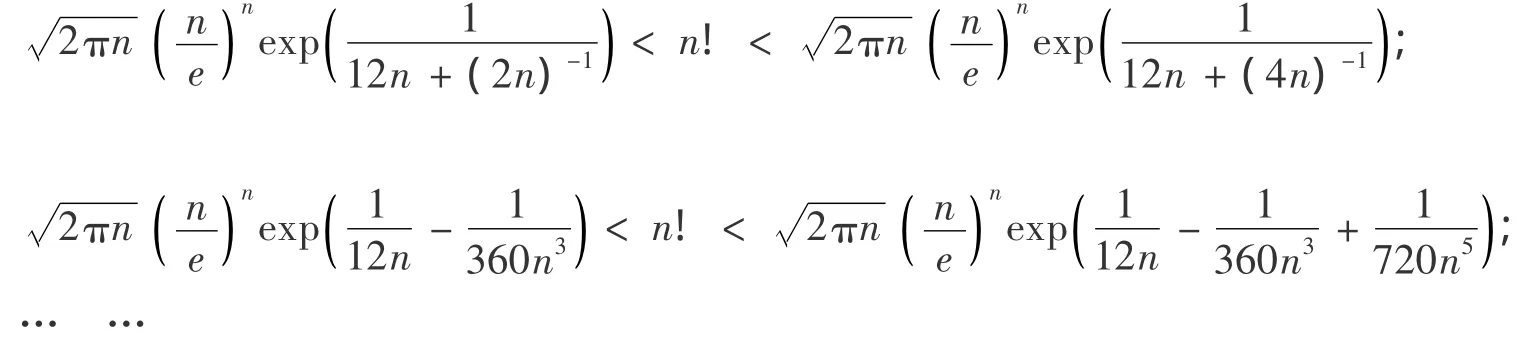
在文献［3］中还有如下结果为

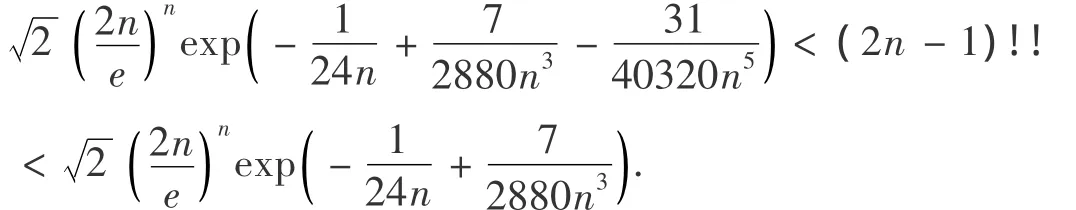
在文献［4］中有如下结果:

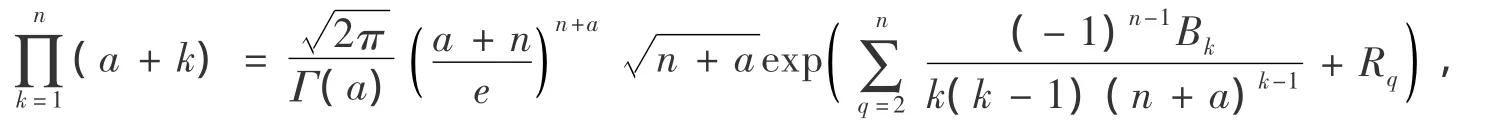
kk函数的最大值．

将Stirling公式再进一步拓展，以期得到等差数列乘积的数值逼近表达式．

1 等差数列乘积的数值逼近

首先把Stirling公式中的自然数乘积n!=1·2…n拓展为等差数列乘积:

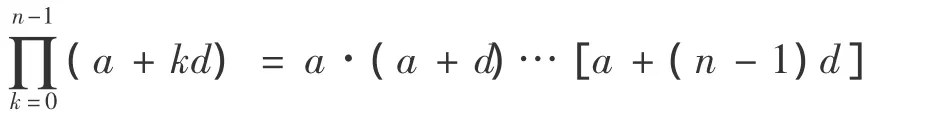
1．1 等差数列乘积的表达式

定理1 设a ＞0，d ＞0，n∈N*，则:

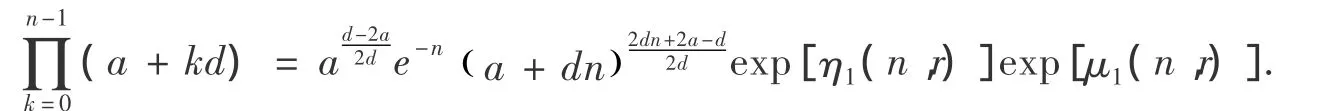
其中:

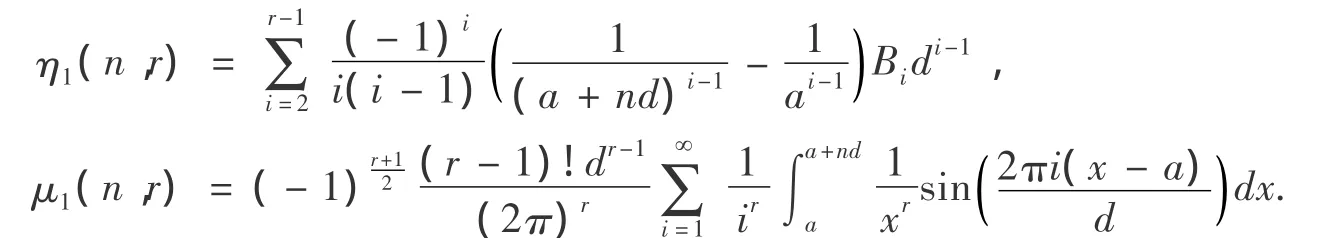
证明:根据Euler-Marclaurin公式，又由f(x)=ln x的n阶导数:

在［a，+∞)是绝对连续的，再取t=0，h=d，b=a+nd，又根据Bernoulli函数性质中的Bk(0)=)，Bernoulli数中的 B2k+1=0，则取 r为某一奇数，有Br(0)=0．可得:

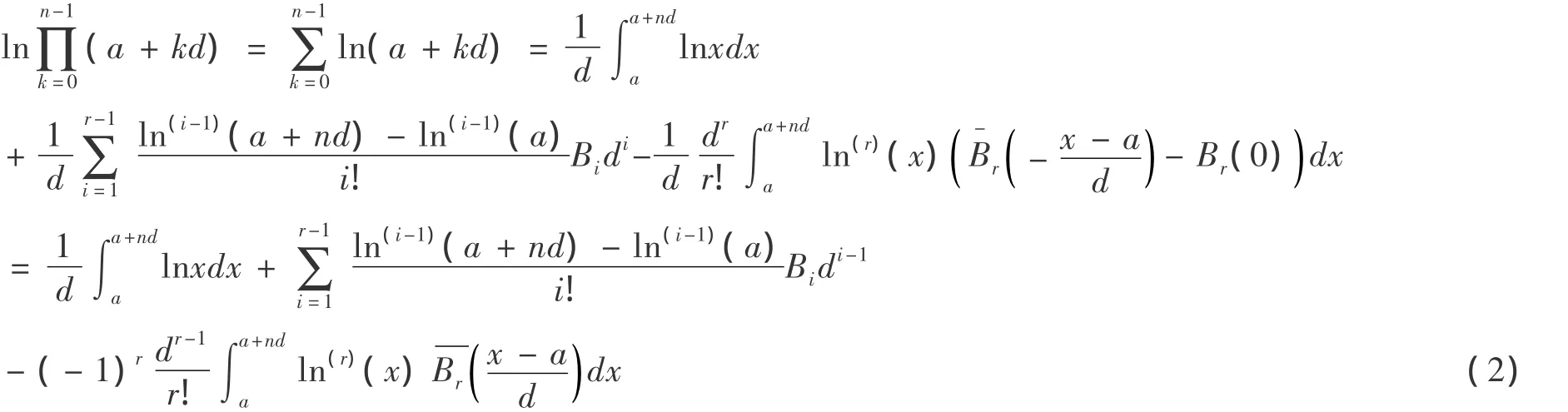
分别对(2)中的3个表达式变形得:

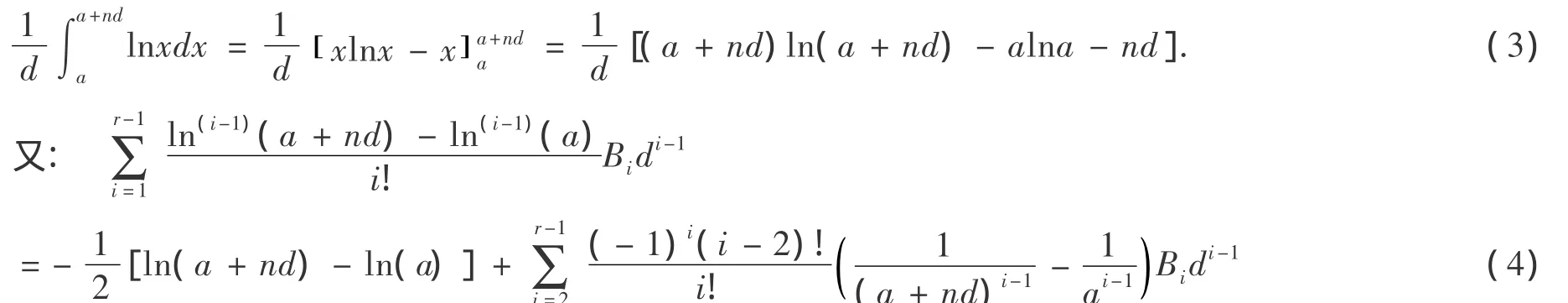
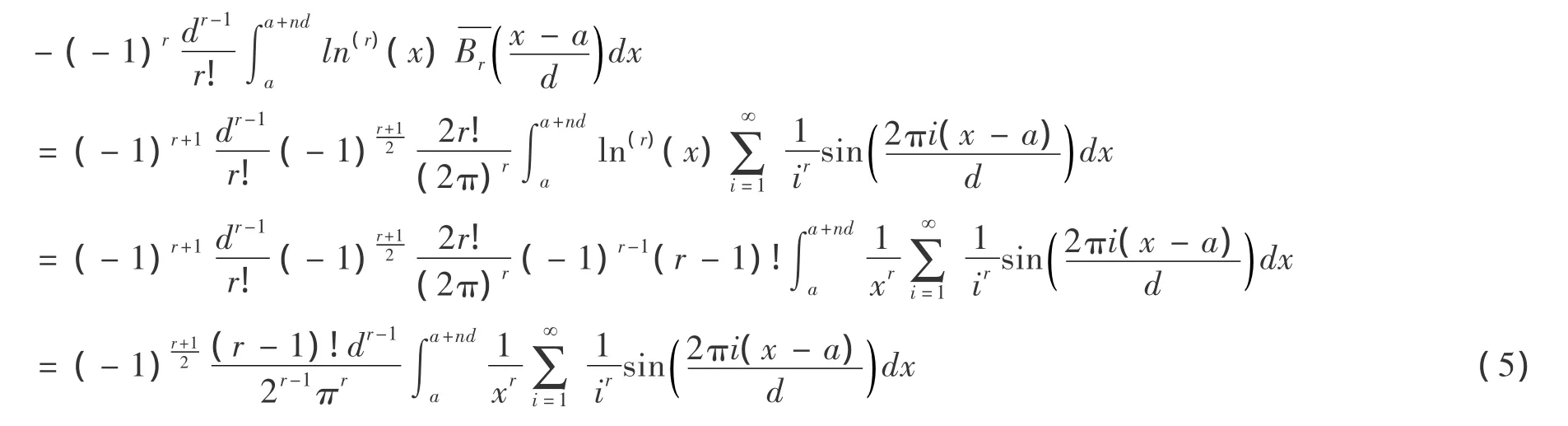
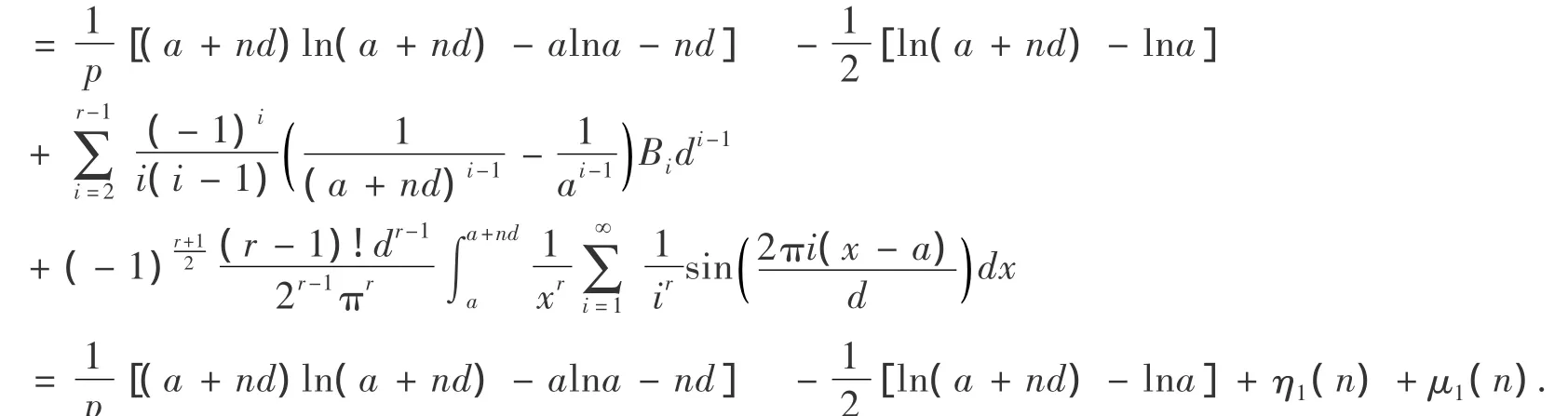
即证:

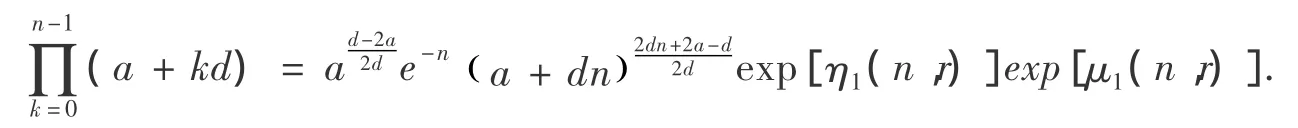
由于μ1(n)含有积分式，需要简化，有下面结果．可以作为当等差数列乘积的近似表达式的一个误差估计．

证明:

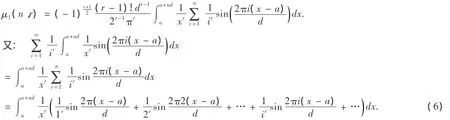
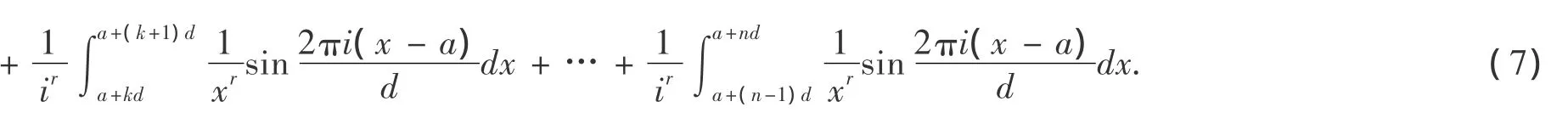
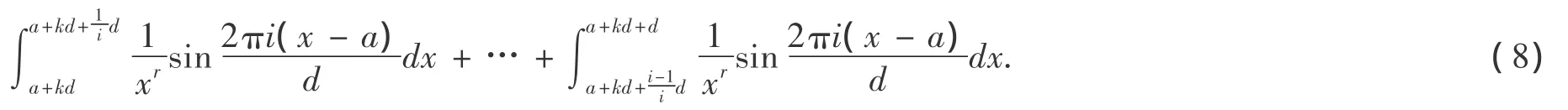
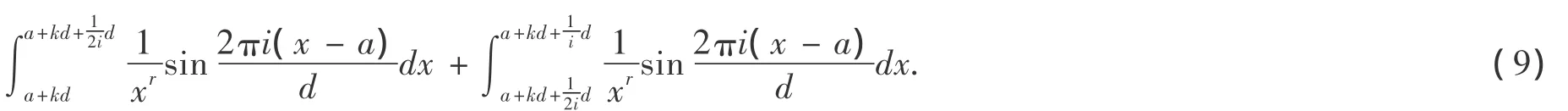
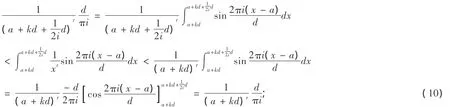
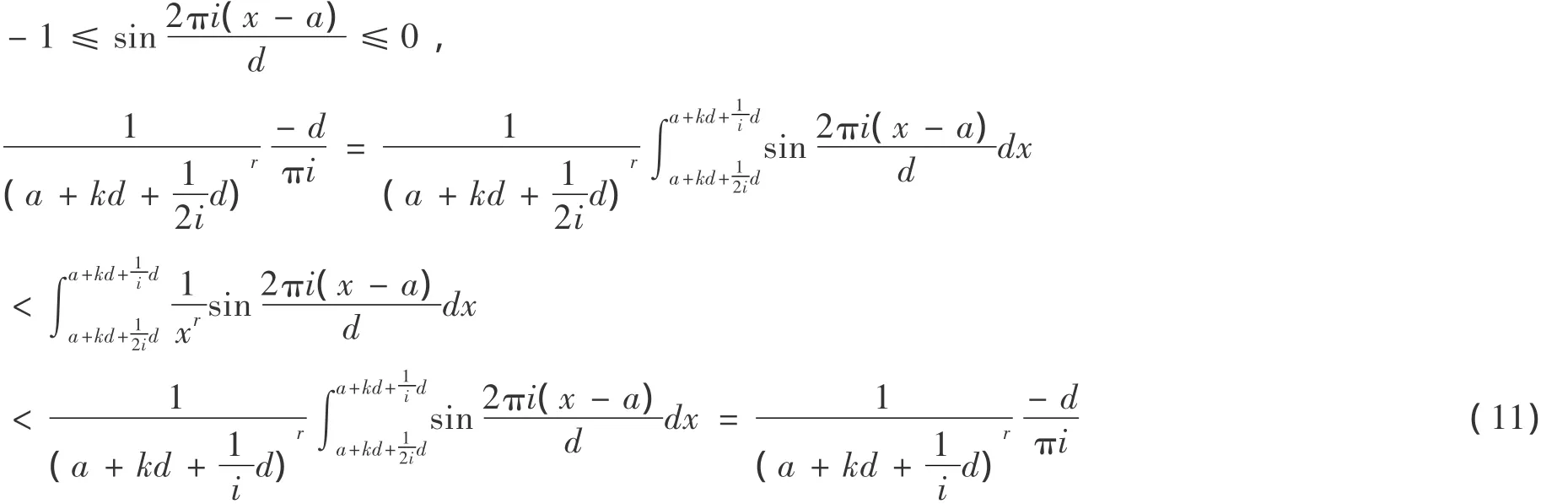
将(10)，(11)代入(9)得:

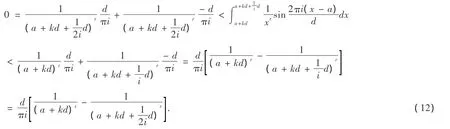
同理，依次可以推得i个不等式，最后一个为:

将(12)(13)等i个不等式相加得:

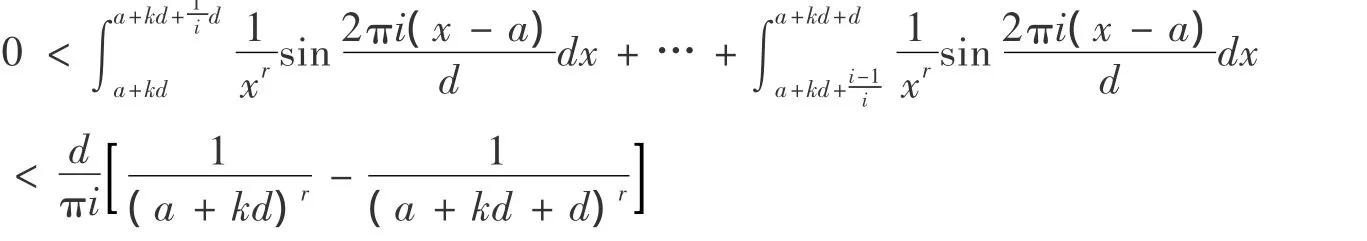
由(7)，对(14)中k相加，得:

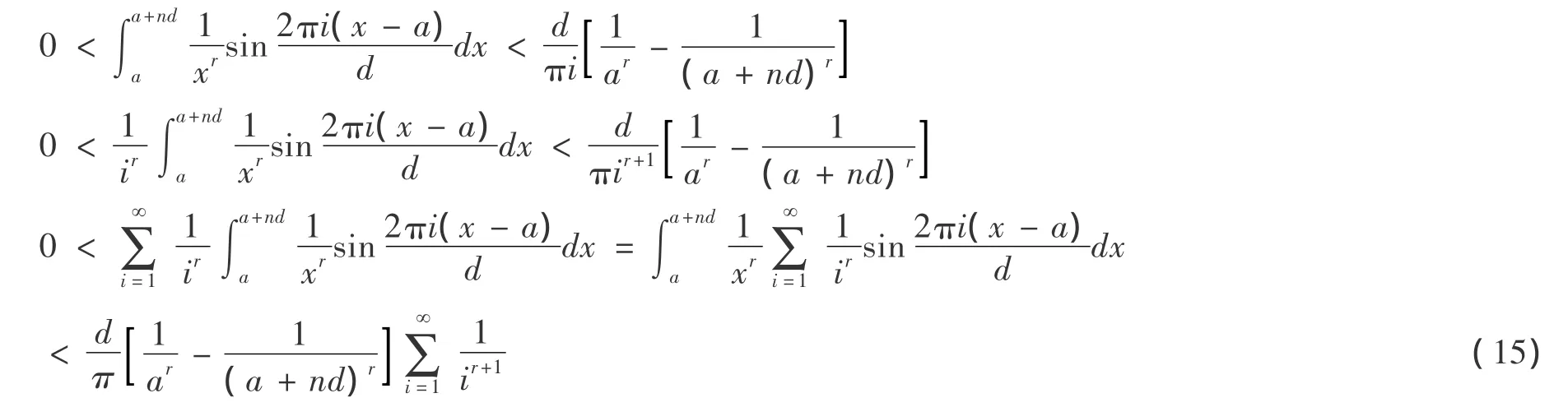
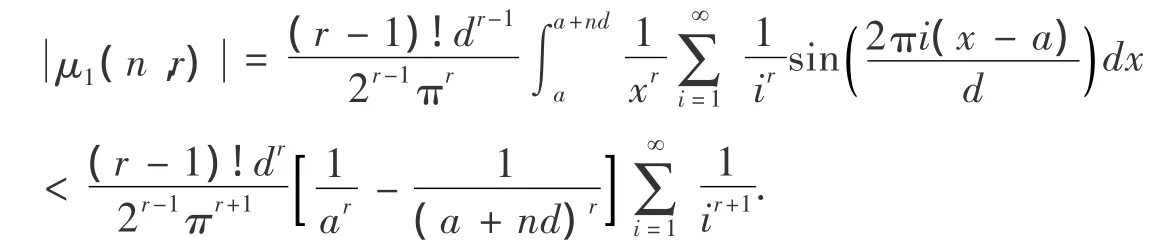
1．2 相关推论

为了将定理1的公式变成另一简洁形式．有下面推论1．

推论1 设a ＞0，d ＞0，n∈N*，则:

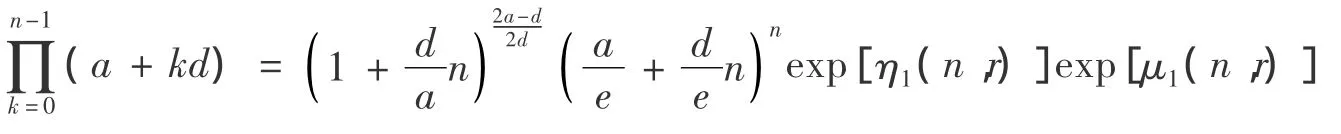
推论2 设a ＞0，d ＞0，n∈N*，则:

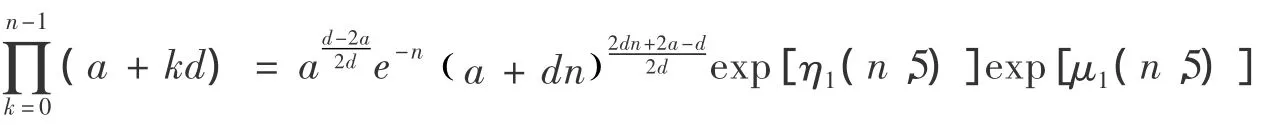
证明:在定理1，2．2 中，对于:

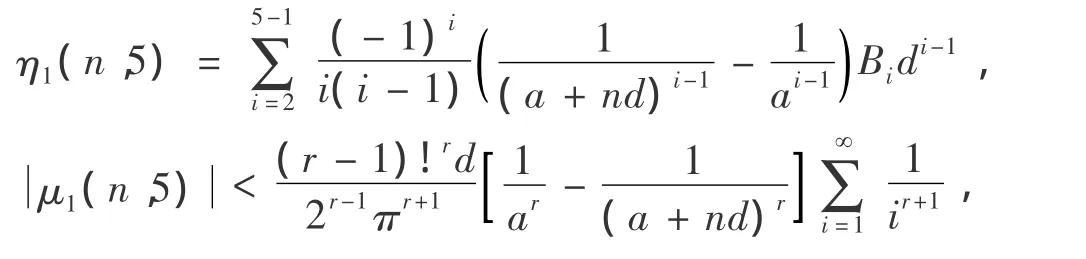
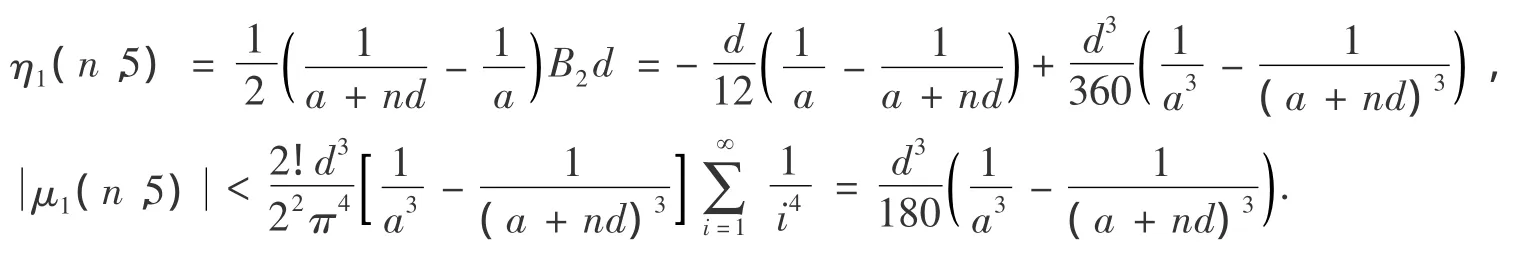
由定理2推导过程的(15)，r=5，下式:

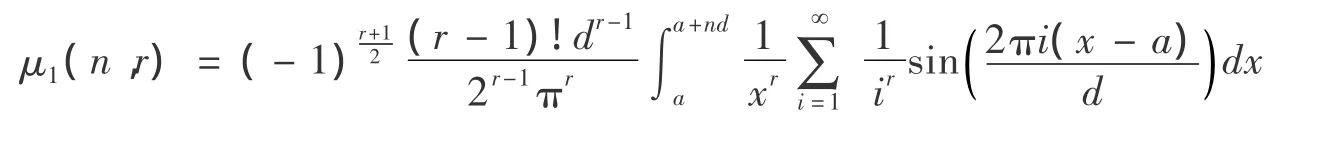
推论3设a ＞0，d ＞0，n∈N*，则:

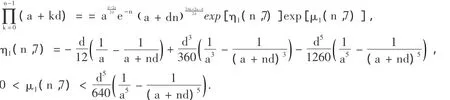
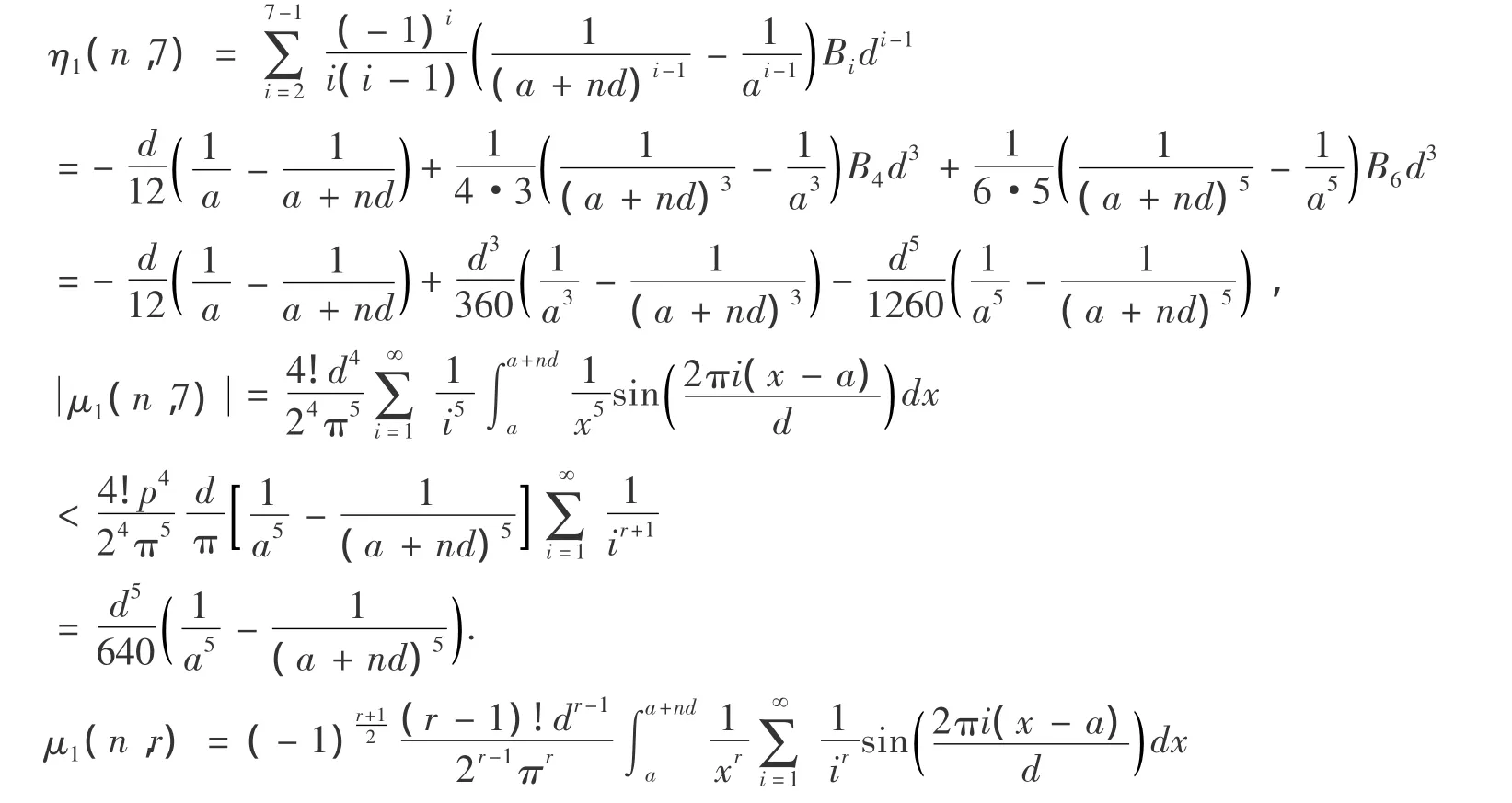
有关a，d可取整数之外的其它任意正数，比如是小数或无理数，会得到大量代数式，其例子不再列举．

因此，定理1推广了n!估计式，拓展了Stirling公式的应用范围．

2 数值逼近表达式的实例检验

对于推论3的数值逼近的精度，采用数学软件:MATHEMATICA8．0，编写程序检验精确度．取:数值原值表达式:

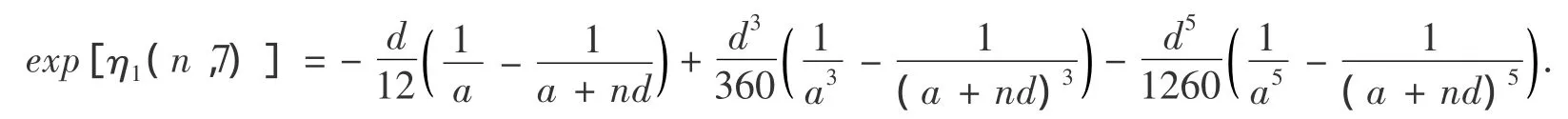
相对误差:H1=(A-B1)/A，H2=(A-B2)/A．

表1 数值逼近表达式B1中变量n对精度的影响

表1说明数值逼近表达式B1中，随变量n的增大，相对误差在增大，基本达到1/10000．

表2 数值逼近表达式B2中变量n对精度的影响

表2说明数值逼近表达式B2中，随变量n的增大，相对误差在增大，基本达到1/1014．

3 结 论

定理1中给出的等差数列乘积的数值逼近表达式，拓展了Stirling公式．在适用范围方面是最宽泛的一个结果．

定理2中给出的等差数列乘积的数值逼近表达式的误差估计表达式，是经过较细致严密的缩放，因此数值精度在理论上有一个较优的估计．

通过计算机编程验证，举出实例说明文中结论可靠实用．对于如何精简近似表达式、提高数值逼近精度、推导其它类型数列乘积的数值逼近表达式将是继续探索的方向．

Stirling公式在数学分析、数论、概率论及相关领域有着诸多的重要应用，二项分布和超几何分布的计算问题都可归结为阶乘的计算问题，在产品抽样验收与(n，c)方案中有具体应用．在数学物理方程、计算数学、工程数学应用中的方程问题，通过运用本结论给出的近似表达更为简洁．另外，在代数式推导过程中也有一定的重要应用．按照文中思路，对幂指数列的数值逼近等具有推广借鉴意义．

［1］ L．C．Hsu，LUOXiaonan．OnaTwo-sideInequalityInvolvingStirlingformula［J］．JournalofMathematicalresearchandexposition．1999，19(3)．

［2］ 匡继昌．常用不等式［M］．3版，济南:山东科技出版社．2004．

［3］ 杨必成．关于阶乘的一些新不等式［J］．广东教育学院学报，2002(2):1-4．

［4］ 谢子填．Stirling公式的一个推广［J］．数学实践与认识，2006(6):331-333．

［5］ Stirling＇sFormula［DB/OL］．http://www．sosmath．com/calculus/sequence/stirling/stirling．html

［6］ Problem2-Stirling＇sFormula．1999，19(3)［EB/OL］．http://web．yl．is．s．u-tokyo．ac．jp/～ affeldt/examination/examination/node97．html．