限制李超代数环面秩的一个重要性质
高孝成,姚 艳
(黑河学院数学系,黑龙江黑河164300)
李超代数是在李代数的基础上发展起来的一个代数学分支,而李代数这一概念是由挪威数学家M.S.Lie在19世纪后期研究连续变换群时引进的.拓扑学中的李超代数通常是特征p域上的李超代数(即模李超代数),尤其是有限域上李超代数[1].目前,模李代数与非模李超代数都已经有相对完整的结构理论.在1977年,李超代数理论的奠基人之一,著名的数学家V.G.Kac在有限维、特征零情形,给出了单李超代数的完全分类,1998年,Kac又完成了特征零代数闭域上无限维单的线性紧致李超代数的分类[2],无限维线性紧致李超代数也有完全分类[3];典型模李代数和代数群的表示[4],特征零典型李超代数、另外李超代数的表示也都取得了长足的发展.这样自然要考虑到素特征域上的有限维单李超代数(模李超代数)的情况,即模李超代数的分类问题.
限制李代数的概念在模李代数理论中起着非常重要的作用,有限维模李代数的分类和表示首先是基于限制李代数上的[5-6].因此,将模李代数限制理论平行推广到模李超代数中是十分必要的,见文献[7-10].首先,每个模李超代数都可以嵌入到它的一个包络中,从而利用映射研究结构问题.其次,容易证明模李超代数的任何有限维不可约表示均具有唯一性特征.这样,我们可以象模李代数情形一样对表示问题进行深入细致的研究.对于模李代数而言,环面、环面秩是限制理论中非常重要的概念,将它们推广到限制李超代数中进行研究,对于限制李超代数理论的作用也是基础性的.本文中,Z表示整数集,没有特殊说明时,F表示特征为素数p>2的域.
1 预备知识
在一般的域F上:
定义1.1 设A是域F上的线性空间,A称作F上的代数,如果除了数乘和A的加法运算外,A还有一个乘法运算(用xy表示x与y的乘积,∀x,y∈A),并且满足以下条件:
(i)x(y+z)=xy+xz,(y+z)x=yx+zx,
(ii)λ(xy)=(λx)y=x(λy),∀x,y,z∈A,∀λ∈F.
如果代数A是F上的有限维线性空间,则称A为F上的有限维代数.
如果代数A的乘法满足结合律,则称A为结合代数;如果代数A的乘法满足交换律,则称A为交换代数.
如果代数A的乘法满足以下条件:
(i)x2=0,∀x∈ A,
(ii)x(yz)+y(zx)+z(xy)=0,∀x,y,z∈A,(Jacobi等式),
则称A为李代数.
定义 1.2[11]设 L=L0-⊕ L1-是域 F 上的一个Z2-阶化代数,L中的乘法用方括号[,]表示,对于L中任意齐次元素a,b,c,若以下条件被满足:
(1)[a,b] = - (- 1)|a||b|[a,b] (超反对称)
(2)(- 1)|a||c|[a,[b,c]]+(- 1)|a||b|[b,[c,a]] +(- 1)|b||c|[c,[a,b]] =0 (超Jacobi-恒等式)
则称L是一个李超代数.
在素特征的域F上:

其中Si(a,b)是由如下公式唯一确定的:
p-1

定义1.4 设(L,[p])与(L',[p]')是两个限制李超代数,φ:L→ L'是李超代数同态.若φ|L-
0:→是一个李代数限制同态,则称φ是限制李超代数(L,[p])到(L',[p]')的限制同态(p-同态).
(1)一个包含限制李超代数(G,[p])和一个李超代数的单同态l:L→G的(G,[P],l)叫做L的一个限制包络,
(2)L的一个限制包络(G,[p])叫做泛限制包络,如果下面的泛性质成立:对于每一个限制李超代数(H,[p]')和每一个李超代数同态f:L→H,刚好存在一个限制同态 g:(G,[p])→ (H,[p]'),使得g◦l=f限制包络也称为p-包络.
为了计算的方便,给出以下引理:
引理1.1 设限制李超代数(L,[p])的子代数为K,K[p]为包含K的(L,[p])的最小的p- 子代数,则有

其中,αi∈ F,ki∈ ℕ ,xi∈ K0-,y ∈ K1-,y ∈是由生成的的限制李子代数.
在李超代数中,也有类似李代数限制包络的结论.
引理1.2 每一个有限维李超代数都有一个有限维的限制包络.
2 环面秩
下面,设L是有限维李超代数.
定义2.1 设T是限制李超代数(L,[p])的一个子代数,若满足:
(1)T是L的Abel p-子代数,
(3)对于任意x∈T,x为L的p-半单元,即存在 αi∈F,使得
则称T为L的一个环面.
定义2.2 设K是李超代数L的子代数,(G,[p],l)为 L 的 p - 包络,K[p]=(l(K))[p],T 是K[p]/K[p]∩ C(G)的环面,称

为K在L中的环面秩,tr(L):=tr(L,L)为L的绝对环面秩.
注记2.1设H与K是有限维李超代数L的子代数,且H⊂K,则
(1)L的p-包络选取不影响子代数K或H在L中的环面秩,
(2)tr(H)≤tr(K)
(3)tr(H,K)≤tr(H,L)≤tr(K,L)
(4)不考虑中心的影响,环面秩最大的环面即为维数最大的环面.
3 结 论
定理3.1 设H,K分别是有限维限制李超代数(L,[p])的子代数,且 H ⊂ K.
若 tr(H,L)=tr(L),则 tr(H,K)=tr(K).
证明:根据引理1.1,可设L[p]为L的有限维p- 包络.由引理1.2,
取 H[p]/(H[p]∩ C(L[p]))的 p-理想:
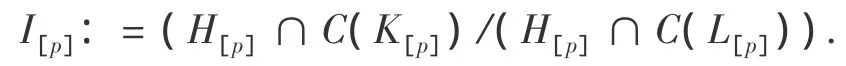
易见,
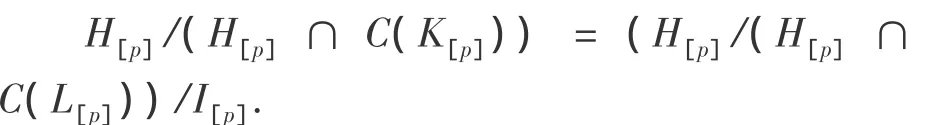
方便起见,对于有限维李超代数L,记mt(L)为L的环面的最大维数,即
mt(L):=max{dim T|T为L的环面}
则

从而,

即

这样,
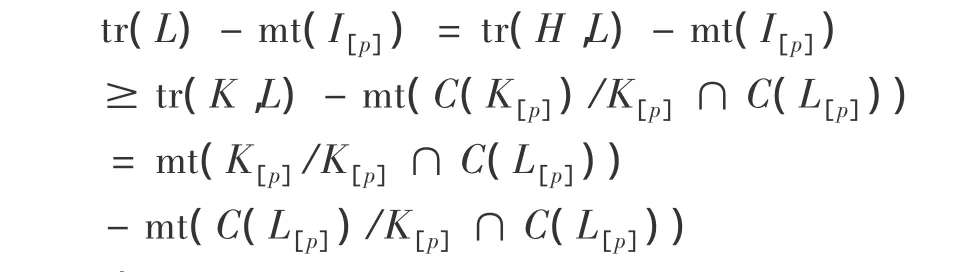
由(6),

应用(5)可得,
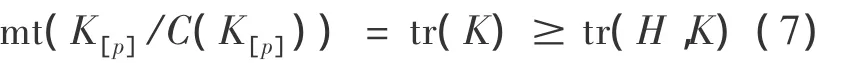
最后,由(4)与(7),知 tr(H,K)=tr(K).结论得证.
本文将环面、环面秩概念推广到限制李超代数中进行研究,给出了限制李超代数环面秩的一个重要性质,为限制李代数的研究奠定了理论基础.
[1] S.Berman,Y.Gao,Y.S.Krylyuk.Quantum Tori and the structure of elliptic quasi-simple Lie algebras[J].J.Funct.Anal,1996,135:338-339.
[2] Y.Su,R.Zhang.Cohomology of Lie superalgevras sl(m-n)and osp(2 -2n)[J].Proc.London Math.Soc,2007,94:91-136.
[3] W.D.Liu,Y.Z.Zhang.X.L.Wang.The derivation algebra of the Cartan type Lie superalgebra HO[J].Comn.Algebra,2005,33:2131-2143.
[4] J.C.Jantzen.Representations of Lie algebras in positive characteristic[J].Representation Theory of Algebraic Groups and Quantum Groups,2002,1:1-8.
[5] Walterde Gruyter,Berlinand H.Strade.Simple Lie Algebras over Fields of Positive Characteristic[M].New York:Die Deutsche Bibliothek,2004.
[6] H.Strade,R.Farnsteiner.Modular Lie Algebras and Their Representations[M].New York:Monographys and Texbooks Pure Appl.Math,1988:116.
[7] Yu.Kochetkov,D.Leites.Simple Lie algebras in characteristic 2 recovered from superlgebras and on the notion of a simple finite group[J].Contemp.Math,1992,131(2):59-67.
[8] LY Chen,DJ Meng,YZ Zhang.The Frattini subalgebra of restricted Lie superalgebras[J].ActaMath Sin.,EnglishSer,2006,22(5):1343-1356.
[9] WD. Liu. Induced modules of restricted Lie superalgebras[J].Northeast Math.,2005,21(1):54-60.
[10] V.M.Petrogradski.Identities in the enveloping algebrasJP for modular Lie superalgebras[J].Algebra,1992,145:1-21.
[11]刘冬丽.Cartan型模李超代数的环面及导子代数[D].哈尔滨:哈尔滨师范大学,2008,6.

