以“惑”为诱教学方法在八年级数学教学中的应用研究
张建飞
(重庆市第八中学,重庆,400030)
新课程理念倡导数学教学,以学生为本,关注学生学习动机的激发,关注学生学习兴趣、信心及创造力的培养,以“惑”为诱教学方法正是在此背景下应运而生,这种方法注重授予学生在课堂教学中的话语权,注重以学生为本,可有效提高教学效率,达成教学目标。
一、以“惑”为诱教学方法概念阐述
“惑”在认知心理学领域中是指在外在因素作用下个体产生心理迷乱的一种心理状态,但它是一种不稳定的过渡状态,个体会在原有心理水平与可能达到的心理水平之间达到平衡,并在这一平衡状态下逐渐产生趋向于可能水平的思考和行为。因此,以“惑”为诱的教学方法,正是教师利用“惑”这一外界刺激,通过主动发现、制造惑去刺激学生,让学生产生求知欲,并理清、辨析惑,进而解答疑惑达成教学目标的一种教学方法,在具体应用中一般有“设惑”“厘惑”“解惑”“思惑”四个步骤。
二、八年级数学应用以“惑”为诱教学方法的要求
认知发展心理学认为,“个体学习与其心理发展水平有相互依存、促进的关系,八年级学生正处于经验背景下的逻辑抽象思维阶段,学习的方式方法有潜在规定性”,教师应用以“惑”为诱教学方法需遵循以下要求:
(一)创设有效的“惑境”
有效的“惑境”主要表现在情感性和动力性方面。一方面,教师在情感性上需要引发学生的困惑心理,使学生面对“惑”时能有足够的信心,让学生实现由“惑”而“知”的可能性飞跃;另一方面,教师在动力性上需按照最近发展区理论中强调的“跳一跳,摘果子”原则为学生创设难度适中的惑,激发学生内在的求知欲,让学生既不会因“惑”太难而放弃,也不会因太容易而失去兴趣。
(二)关注“惑”的个体性
由于学生原有的知识结构、认知水平存在差异,在同一“惑境”中,不同学生对“惑”呈现出不同的个体性。如就产生“惑”的原因来说,有些学生会因原有知识准备不足而困惑,有些学生会因学习能力不足而困惑,更有些学生会因审题出现偏差而困惑。教师面对学生“惑”的个体差异性,在应用以“惑”为诱教学方法时,需尽量照顾到每一位学生,与他们交流,了解学生的“惑”,了解学生产生“惑”的具体原因,并采取一些措施指导每一位学生解决他们所面临的“惑”,使学生达成由“惑”至“知”的目的。
(三)倡导学生的探究
学生自我在以“惑”为诱的教学方法实施过程中起着十分重要的作用,自我解惑重视的是个体自主学习的过程,设置“惑”的目的是通过引发学生认知的失效与学生与之俱来的认知欲形成冲突,而自我解惑正是学生在求知欲的驱动下主动探究“惑”的过程,这能进一步激发学生的求知欲望,提高学生的学习兴趣。欲达此目的,教师一方面需要降低学生探究的“危险系数”,让学生享受自主探究的乐趣及自我解惑的成就感;另一方面,在学生探究失败时,需采取有效措施使学生不因此而萎靡不振,同时引导学生总结失败的经验教训,避免犯同类的错误。
(四)重视方向的引导
解惑的过程中,教师应允许学生试误,但当学生反复试误无果时,教师需充分发挥引导者的作用。教师对学生思维的引导,需要蹲下身,放下架子,站在和学生一样的高度上,去发现、满足学生至“知”的需要,和学生一起探索。只有这样,教师才能与学生平等对话,进行无障碍交流,实现学生顺利解“惑”至“知”的教学目标。
三、以“惑”为诱教学方法在八年级数学教学中的应用案例
以梯形面积的计算为例,从四个步骤去分析此教学方法在八年级数学中的应用。
(一)“设惑”,即创设教学情境,使学生产生困惑
师:甲、乙两村合修一长80米、高5米的水坝,甲村修到一半时乙村接着修。现县水利局要给这一工程以每方50元的补贴,两村因图纸丢失而无法确定补贴金额而焦头烂额。在座的同学若是村长,能否解决这一难题?
(生听完问题后相互讨论,一致认为条件不够,无法解决)
师:为什么不能解决?
生1:要算总金额,需算出拦水坝的体积,拦水坝的长80米是已知的,只需计算出拦水坝的横截面——梯形的面积即可,梯形的面积=(上底+下底)×高÷2,但在此处只有高5米是已知的,故不能解决。
师:其他同学同意吗?
(生们一致表示同意)
师:同学们据已学数学知识推断这问题无法解决,可这问题又必须解决,这该如何是好?其实这问题可解,同学们可设法攻破这一难题吗?
这时,学生们脸上露出疑惑,感到难以置信。不少学生还在嘀咕:明明是条件不够,老师怎么说问题可解,这是怎么个解法呢?可见,这一问题引发了认知上的冲突,学生产生了困惑。
(二)“厘惑”,即与学生一起辨析惑
师:解决这一问题的关键在哪呢?
生2:知道上、下底的长度。
师:同学们还有其他不同意见吗?
生3:知道上、下底之和也可。
其他同学纷纷表示赞同。此时,学生已将思考的焦点从“能不能”的困惑转移到“怎么做”与具体解惑问题上了。
(三)“解惑”,即启发、引导学生解决惑
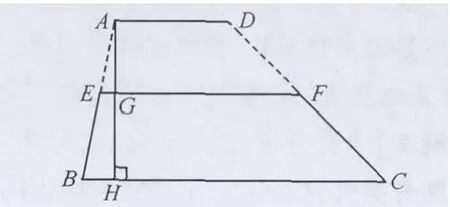
图1
师:同学们可画出梯形的草图,标明已知量,想想上、下底的长度或上、下底之和。同学们可相互交流讨论。
师:找到解决的办法了吗?
(几分钟后,同学们都说没有,但眼中闪烁着渴望)
师:请学生4上讲台画出草图并标明已知量。
(生4画出的草图如图1所示。梯形ABCD是水坝的拦截面,CD为拦水坡,实线为甲村完成的部分,虚线为乙村完成的部分,高AH为5米,是已知的,线段EF可量)
师(夸生4画得好):还有其他遗漏的条件吗?同学们赶紧阅读题目。
生5:甲村修到高度的一半,即AG=GH=2.5米。
师:还有其他被遗漏的条件吗?
(同学们摇头示意没有)
师(用书遮住梯形的虚线部提示):这是个什么形?
生齐:梯形。
师:一共有几个梯形?梯形有什么性质?
生齐:共3个,梯形的两底相互平行。
(此时,不少同学暗喜大声说:梯形中有3条平行线,即AD∥EF∥BC)
师:将条件AD∥EF∥BC与AG=GH放在一起,你们想到什么呢?
(正在思考的同学们恍然大悟,异口同声说:平行线等分线段定理)
师:谁能将这一个定理解释一下?
生6(自告奋勇):如果一组平行线在一条直线上截得的线段相等,那么它在其他线段上截得的线段也相等。
师:据此定理,我们能推出什么呢?
学生一起答:AE=BE,DF=CF,即E、F分别为线段AB、CD的中点,线段EF为梯形的中位线。由以上条件,可算出梯形的面积,S梯形ABCD=1/2(AD+BC)·AH=1/2·2EF·AH=EF·AH。
师:至此,我们顺利帮村长们解决了难题,也学会了梯形面积的另一种计算方法——中位线×高。
(四)“思惑”,即反思解惑的过程
在此教学案例中,教师将生活中的稍有难度的问题作为切入点,使学生产生困惑,产生认知冲突,从而激发学生思考和探究的积极性,且课堂气氛活跃。
[1]林崇德.发展心理学[M].北京:人民教育出版社,1995.
[2]黄晓学.从“惑”到“知”——数学教学重学术认识的发生原理[D].南京:南京师范大学教育科学学院,2006.
[3]莎婷婷.美国数学探究式教学案例特点研究[D].长春:东北师范大学教育科学学院,2010.
[4]何建安.探究式数学在中学数学课堂中的应用和创新[D].兰州:西北师范大学教育科学学院,2004.

