涡环物理特征的研究

向 阳，刘 洪，吴镇远

（1.上海交通大学 航空航天学院，上海 200240；2.上海交通大学 吴镇远空气动力学中心，上海 200240）

0 引 言

鱼的游动和昆虫等动物的飞行所产生的非定常流动中，涡的形成和脱落是一种非常重要的现象。根据Helmholtz原理，由于涡管封闭而形成的涡环是一种最基本的涡结构。针对涡环的流体动力以及在生物推进中的作用，流体力学学者和生物学学者进行了大量的研究。Shariff［1］对涡环的形成、传输以及产生装置对涡环的影响做了全面的回顾和总结，同时Dabiri［2］进一步揭示了涡环的生长模式在生物推进中的作用以及指出在生物推进过程中存在涡环的最佳形成时间。除此之外，Dickinson［3－4］和 Fish［5］都指出鱼和鸟运动过程中是不断产生涡环的过程并进一步分析涡环的形成和传输过程。所以基于涡环的研究能揭示非定常流体动力的机理和本质。

Ruiz［6］通过实验研究涡环形成过程中产生的力，分析非定常力的增强主要是因为涡环从周围流体中不断夹带流体以及涡环本身的附加质量。所以涡环的形成尤其是其夹带流体的过程一直是研究的重点。Maxworthy［7］通过活塞装置证实了涡环的形成过程不断夹带流体，Dabiri［8］通过外流动减缓涡环的传输速度研究涡环的夹带过程，发现形成时间比较小的涡环的夹带流体占涡环总体积的30%～40%。Olcay［9］通过实验进一步研究了不同形成时间下涡环的夹带体积的比例，发现当形成时间比较小时，随着形成时间的增大，涡环夹带体积的比例在减小。但是当形成时间进一步增大所带来涡环的夹带体积的变化还没有得到深入的分析。

针对涡环的形成和传输模式，Fraenkel［10］和Saffman［11］基于无粘条件下提出薄核模型，并给涡环的运动学参数（涡环半径、涡核半径、传输速度）与动力学参数（环量、动量、能量）之间的关系。Sullivan［12］根据实验的结果和理论分析，改进了无粘下的薄核理论，提出了有粘下的薄核理论，对涡环物理特征参数之间的关系进行了修正。Didden［13］根据涡页卷起模型分析了活塞装置生成涡环的过程，指出涡环的环量主要来自于活塞出口的剪切作用，并对涡环的能量、动量等物理特征的变化进行分析提出Slug模型。由于无法合理的确定涡环的物理特征参数，进而无法定量的分析涡环物理特征参数随涡环形成的变化。Akhmetov［14］通过实验的方法研究涡环的半径、涡核半径等参数随形成时间的变化规律，获得一些不同于 Gharib［15］结论，同时 Akhmetov［14］没有进一步分析涡环物理特征发生变化的原因。

Gharib［15］发现当涡环的形成时间达到一个数值后，涡环的环量不再进一步增加，也叫涡环发生夹止（Pinch－off）。Gharib［15］利 用 Kelvin－Benjamin 变 分原理存在的能量极值原理解释，并把涡环发生夹止对应的形成时间称为最佳的形成时间。Dabiri［2］、Linden［16］等人认为当涡环达到最佳形成时间后，其推进效率最高。其中Krueger［17］通过实验发现最佳形成时间下涡环所产生的无量纲平均推力最大，该研究从力的角度回答了涡环的最佳生长时间的意义，从能量的角度研究涡环的最佳形成时间意义还需要进一步的研究。

在研究涡环的过程，不能明确的确定涡环的边界限制了进一步定量研究涡环的物理特征。Didden［13］、Gharib［15］等人在确定涡环的物理特征参数，主要是根据涡环的涡量分布情况，模糊的确定涡环的边界。该方法在定量化处理涡环的物理特诊参数存在严重的不足。Dabiri［18］根据拉格朗日拟序方法（LCS）确定涡环的边界，通过该方法确定的涡环不包括涡环的虚拟质量部分。在确定涡环的形成过程所对应的非定常瞬时力，LCS是一种很好的方法，而对于研究涡环的物理特征参数的变化，该方法存在一些不足。

综合上述分析，由于涡环自身物理特征的研究还缺乏深入地研究，进而无法分析涡环形成、演化过程以及相对应的流体动力，也无法解释涡环最佳形成时间的普遍存在性以及最佳形成时间对应的能量最优利用率。为了定量化分析涡环的形成和演化过程，本文采用流函数方法确定涡环的边界并根据涡环的随体坐标系下的流场信息确定涡环的物理特征参数。进一步分析涡环的物理特征参数随形成时间的变化规律以及涡环的夹止所带来的物理参数的变化。同时为了研究涡环的形成和演化所带来流体动力的变化，本文根据Saffman［19］的冲量定理理解涡环形成过程瞬时力的变化，并基于能量分配的观点，分析不同形成时间涡环的传输能和涡旋能的分配比例。

1 研究方法

本文通过数值模拟涡环的形成和演化过程，进而获得涡环的速度和涡量分布。基于涡环随体坐标系，采用流函数方法确定涡环的边界和其它物理特征参数。通过与Gharib［15］等人的实验对比验证计算和参数确定的准确性和合理性。

1.1 数值计算

由于涡环的各向同性的特点，采用不可压轴对称N－S方程求解，获得一个截面的流场信息即可分析整个涡环的特性。

1.1.1 计算条件

计算域的设置如图1。活塞的半径Rp＝1／2D＝7.5mm，L1＝400mm，L2＝50mm，L3＝950mm，H＝200mm。根据UDF定义活塞的运动速度函数Up＝0.1583m／s，采用动网格使活塞沿着轴向方向运动，在活塞的移动距离到达规定的数值后，活塞的速度变为0，进而生成的涡环将继续向下游传输。在FLUENT6.23下进行计算，网格点的总数为61197，计算采用PISO格式，选择层流，时间步长为0.5ms。本文验证了网格的无关性，和时间步长的选取对计算结果的影响，差别都小于1%。

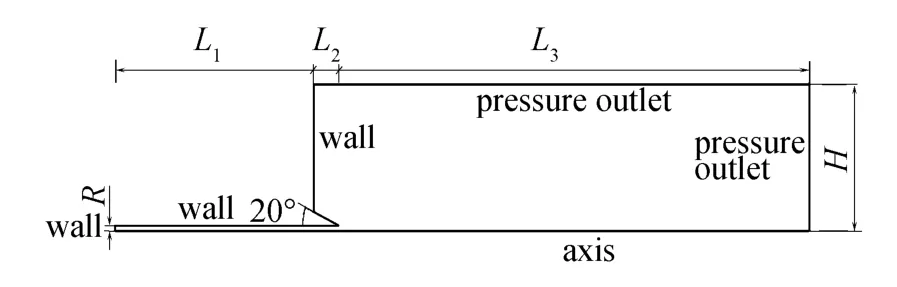
图1 计算域Fig.1 The domain of computation

1.1.2 计算的准确性分析

Gharib［15］研究涡环的形成过程指出，涡环的无量纲环量的计算为：Γ＊＝。图2是在涡环的形成时间为6时，数值计算的结果与Gharib［15］实验获得的结果的对比。从图2中可以看出计算的误差小于5%，是可以接受的。

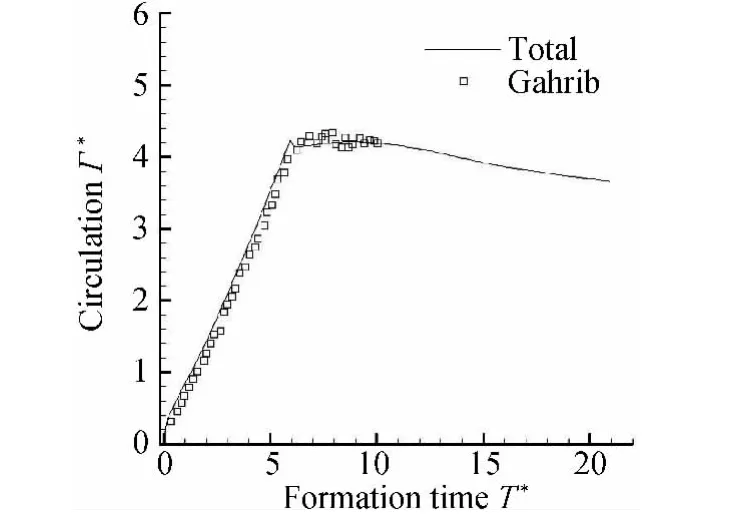
图2 数值计算和实验下的环量对比Fig.2 Comparison of the circulation evolution of the numerical and experimental results

1.2 流函数原理

1.2.1 流函数的计算

根据 Akhmetov［14］在文中的介绍，取柱坐标（r，θ，z），使z轴为涡环的对称轴线，由于涡环存在轴对称特点，所以＝0，＝0，进而涡环内部每一个点的速度只有两个分量即：V（r，z）＝ver＋uez。在固定坐标系下引入流函数ψ，使u＝－，v＝，所以r进一步可知：ψ＝（udr－vdz）。在涡环的随体坐标上，根据 Akhmetov［14］的方法引入流函数ψ0＝［（u－u0）dr－vdz］＝（udr－vdz）－ru0dr＝ψ－u0r2，u0是涡环的传输速度，根据涡核内部涡量最大值处在单位时间移动的单位距离确定。同时进一步定义在r＝0处即涡环的对称轴上（z轴）流函数ψ0的值都为0。在计算流场中任意一点（z1，r1）的流函数ψ0（z1，r1）值时，积分线程L的起点为该点在z轴的投影点（z1，0），故线程L即为点（z1，0）和点（z1，r1）之间的直线线段，所以ψ0（z1，r1）＝［（uu0）dr－vdz］＝r·（u（z1，r）－u0）dr。进而利用该方法可以计算出随体坐标系下流场中各点流函数的值。并画出在涡环随体坐标系下，涡环区域的流函数等值线，如图3。

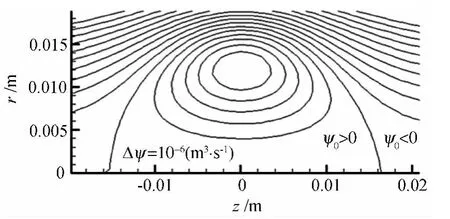
图3 随体坐标下的流函数等值线Fig.3 Streamline pattern

图3可以看出ψ0＝0的等值线包括z轴和一条半圆线，该半圆线把整个区域分成两个部分，ψ0＞0的区域流线封闭，而ψ0＜0的区域流线不封闭，那么把ψ0＝0的封闭曲线包括一条半圆线和z轴的一部分当做涡环切面的边界，改边界绕z轴旋转一周即得涡环的边界。

1.2.2 流函数方法的合理性

在 Gharib［15］、Maxwothy［7］等人在处理实验数据时，大部分都是根据涡环涡量的轮廓来直观确定涡环的边界，图4是同一个涡环的两种不同方法确定的边界。

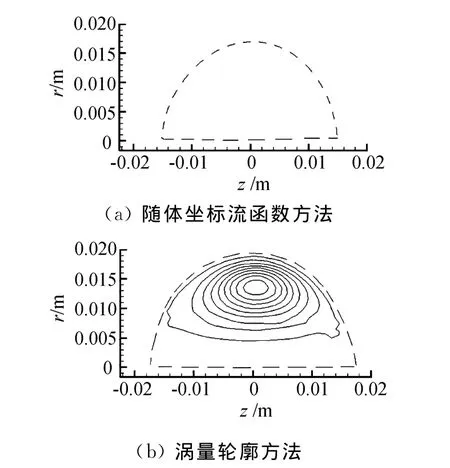
图4 两种不同确定涡环边界方法的比较Fig.4 The comparison of two different methods to define the boundary of vortex ring

图4中的虚线为两种方法确定涡环的边界，图4（a）是根据流函数方法定量的确定涡环的边界，而图4（b）是根据涡量的分布人为画出涡环的边界。从涡量的轮廓和坐标可以看出流函数方法具有合理性，但是直观方法无法定量确定涡环的边界，存在缺陷。

1.2.3 涡环最佳生长时间的确定

Gharib［15］在1998年的实验中分析长冲程活塞的运动产生的涡环，发现涡环的形成时间存在一个极值点，达到该点之后，涡环的环量不再进一步增加，涡环开始形成尾迹，如图5。

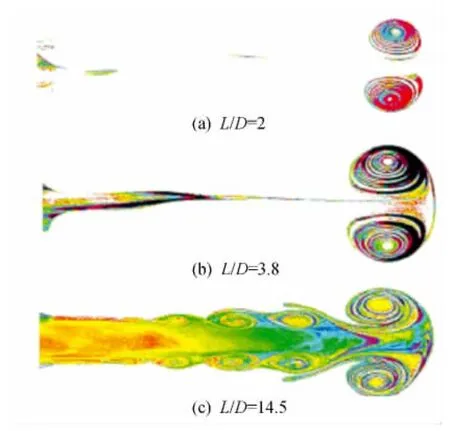
图5 不同形成时间下涡环的形成情况Fig.5 The visualization of vortex rings with different formation time

从图5可以看出当L／D达到4左右时，前缘涡环的大小不再变大，即涡环在此刻发生了夹止，Gharib［15］在确定涡环发生夹止的时间，是根据夹断后的涡环的环量向前延长与总环量增长趋势线的交点，下面采用相同的方法在定义涡环的边界后进一步确定涡环的最佳形成时间。如图6以涡环的总形成时间6为例，其中纵坐标为无量纲环量Г＝，横坐标为涡环的生长时间T＊，其计算方法为T＊＝，t为绝对的物理时间，单位为s。当T＊达到6时活塞不再继续推进，而涡环还在形成和传输的过程，故需要持续观察，而使T＊的值增加。由于涡环的总生长时间为6，故当生长时间达到6之后，流场中总的环量不再进一步增加，由于停止涡［13］的形成，总环量有小幅度的下降。而此时前缘涡环与其尾迹没有分开，所以不能容易地计算出涡环的环量，在涡环继续向下游传输的过程中，与其尾迹分开，而进一步利用流函数方法确定涡环的边界，并计算出其环量。当涡环生长和向下游传输的总的无量纲时间达到15之后，涡环与尾迹完全分开，进而计算其环量和确定涡环的最佳生长时间，如图6所示确定在该速度函数下的涡环最佳形成时间。

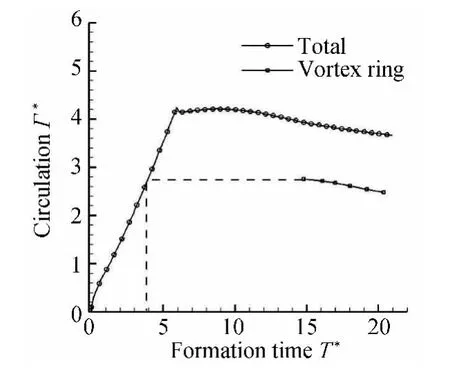
图6 计算涡环的最佳形成时间Fig.6 Calculate the optimal formation time of vortex ring

从图6可以看出涡环的最佳形成时间是4左右，与Gharib［15］的实验结果一致，由于涡环在向下游传输的过程中，涡量有一定的耗散，而使环量有略微的下降。

从上述比较发现根据流函数方法确定涡环的边界是合理的，且能对涡环的众多物理特征提供定量的分析。

1.3 涡环物理特征参数的确定

1.3.1 涡环的运动学参数

涡环的运动学参数包括传输速度U0，涡环的半径R，涡环涡核的半径a，其如图7所示。

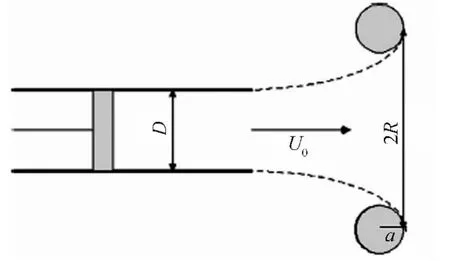
图7 涡环的运动学参数示意图Fig.7 Sketch of the kinetic parameter of vortex ring

在计算随体坐标系下的涡环的流函数值时首先要确定涡环的传输速度，根据涡环中心即涡核内部涡量最大值的地方，在一定时间下移动的距离计算涡环的无量纲传输速度U＊＝，在不同形成时间下涡环的传输速度如图8所示。

由于涡环中心的确定存在一定的误差，所以涡环的传输速度也有一定的误差。从图8可以看出涡环的传输速度在未发生夹止之前类似线性增长，与Shusser［20］依据Slug模型推出的结论一致，而当涡环发生夹止之后涡环的传输速度与生长时间之间的关系发生了变化。根据Shusser［20］在2003年的文章指出在涡环发生夹止时涡环的传输速度满足U0＝，从图8可以发现在涡环的形成时间为4时，P U＊＝≈。在进行一些实验结果和理论值对比后，该传输速度的计算是比较合理的。

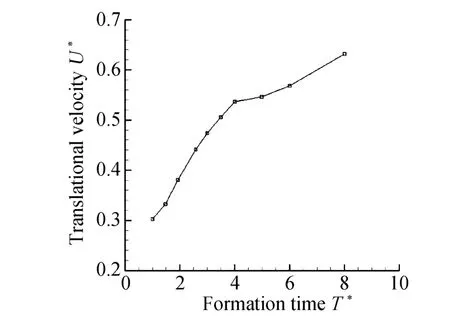
图8 不同形成时间下的涡环的传输速度Fig.8 The translational velocity of vortex ring with different formation time

进一步确定涡环的半径和涡核的半径，首先使坐标随涡环的传输一起运动。在z＝0的平面上记录涡环的轴向速度如图9。

从图9可以看出该平面上的速度存在两个拐点，在拐点之间的速度近似线性的分布，该线性的分布区域即为涡核，所以如上图a为涡核的半径，而R为涡环的半径。

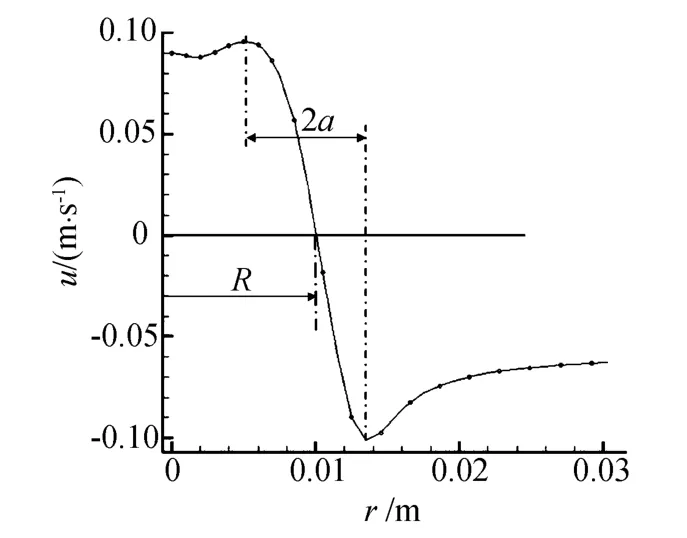
图9 z＝0平面上的轴向速度分布Fig.9 Velocity distribution in the plane z＝0

1.3.2 涡环的动力学参数

涡环的动力学参数主要是涡环的环量、能量和动量。根据流函数方法确定涡环的边界，根据以下公式即可确定涡环的环量、能量和动量：

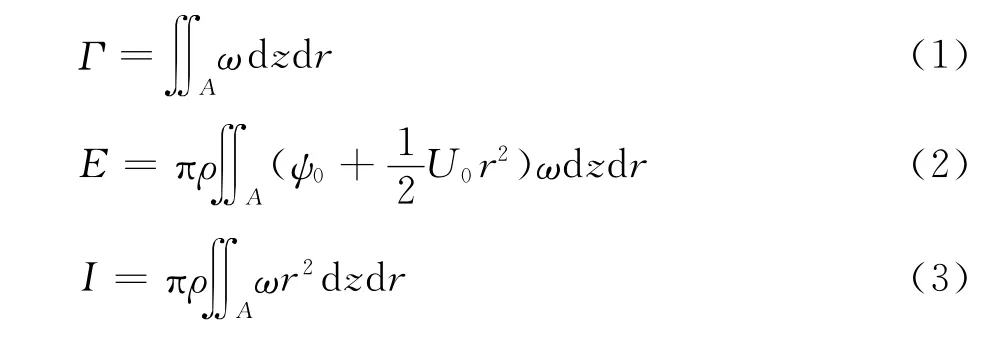
其中A为根据流函数确定的涡环区域，ρ为流体的密度，ω为涡量。根据动量定理以及Saffman［19］的冲量公式，可以计算涡环产生的非定常瞬时力为：

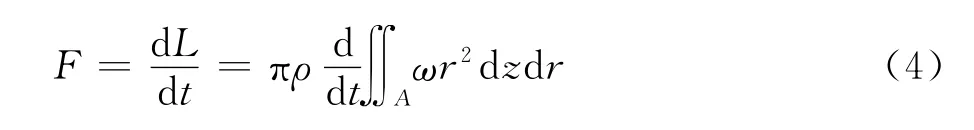
同时把涡环的能量分为传输能和涡旋能，其中传输能的定义为：与涡环的等大小等质量的刚体以相等的传输速度移动所具有的能量，其计算公式如下：

其中，V是根据流函数方法确定的涡环的体积。

2 结果与分析

在 Sharriff［1］、Maxworthy［2］、Gharib［15］以 及Akhmetov［14］等人对涡环的研究中证明涡环的物理特征主要与其形成时间（T＊＝L／D）和雷诺数（Re＝）有关系。本文主要利用流函数方法初步研究涡环的形成时间如何影响涡环的物理特征。

2.1 不同形成时间的涡环运动学特性

采用随体坐标系下的流函数能较好的确定涡环的边界，而由于涡量的耗散以及在确定涡环的如图10是不同形成时间下涡环的边界。

图10可以看出在形成时间较小时涡环无尾迹生成，当形成时间等于5时，涡环的尾迹已经比较明显。Maxwothy［6］和 Dabiri［8］的实验都证明了涡环的体积主要来自于活塞推出的流体和涡环生长过程从周围夹带的流体，进而分析涡环在不同形成时间下的体积组成如图11，其中三角形点表示涡环的总体积，圆形点表示活塞装置中的流体，根据Didden［13］等人的观点认为活塞中的流体基本上都进入涡环内部。

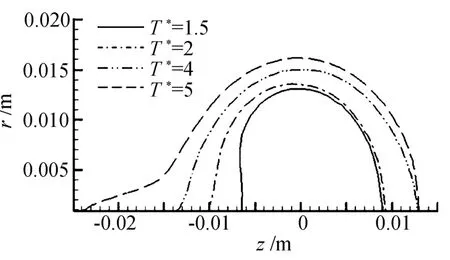
图10 不同形成时间涡环的边界Fig.10 The boundary of vortex ring with different formation time

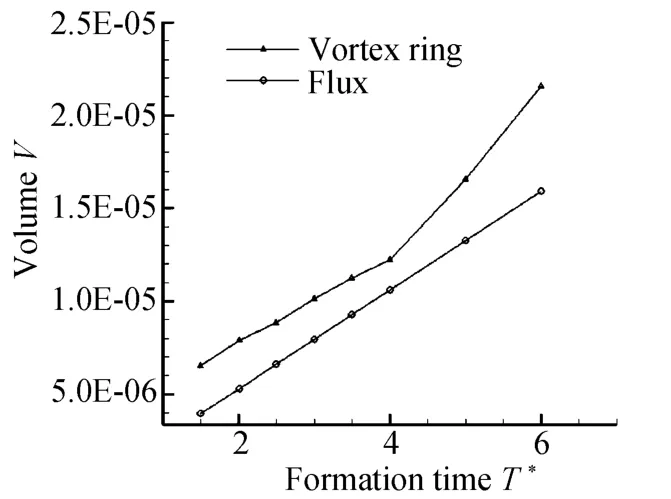
图11 涡环体积及其组成Fig.11 The volumes of vortex and flux

涡环体积的另一部分来自于涡环的夹带过程，不同形成时间涡环的体积中夹带的部分所占的比重不同，如图12。

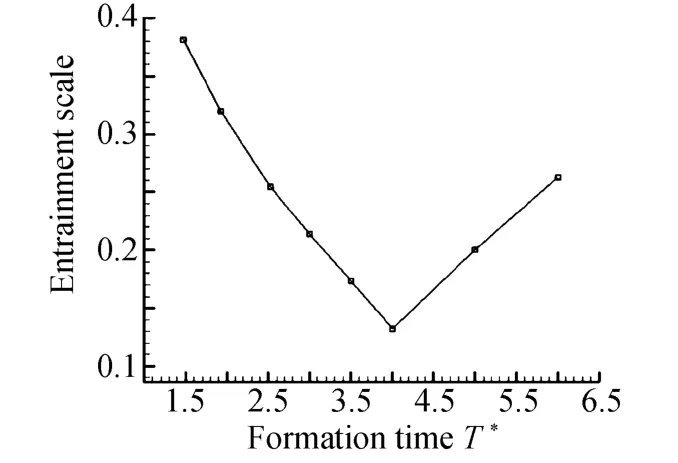
图12 不同形成时间涡环的夹带流体情况Fig.12 Fluid entrainment by vortex ring with different formation time

从图12可以看出在形成时间较小时，涡环中夹带的流体的比例在30%～40%之间与Dabiri［8］2005年的实验结果一致，并且随着形成时间的增大，涡环的夹带部分所占的比例在逐渐降低，而随后涡环的夹带部分开始增大。尾迹中开始生成新的小的涡环，而小涡环的夹带能力很强，所以使整个涡环的夹带能力增强。

不同形成时间下涡环的夹带能力不同，其它运动学参数也随形成时间变化而变化。根据前文中提到的方法确定涡环的半径，涡核半径并计算以下无量纲量：

图13是涡环的无量纲参数随形成时间的变化。从图中可以看出涡环的半径随形成时间类似线性的变化。涡核的半径在形成时间较小时变化比较明显，而当形成时间大于4后，增长趋势不再明显。

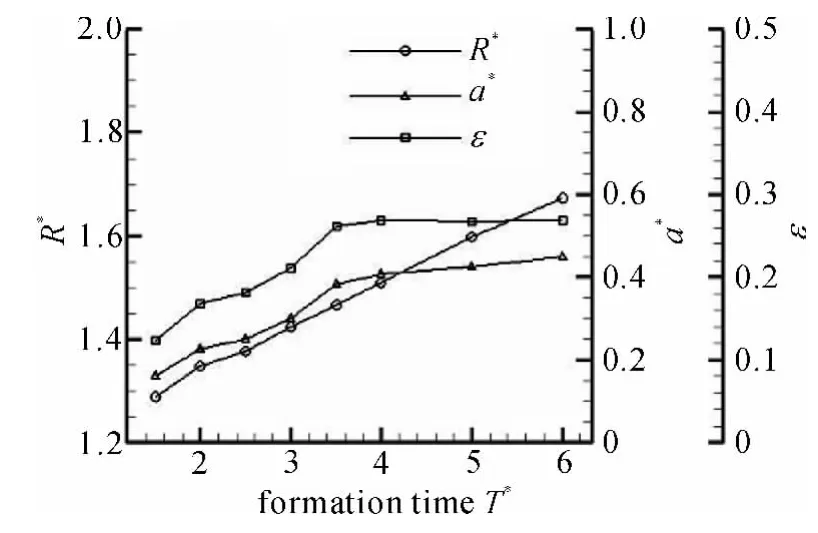
图13 不同形成时间的涡环运动学参数Fig.13 The parameters of vortex ring with different formation time

2.2 不同形成时间的涡环的动力学特性

Gharib［15］在解释涡环的夹止现象时，引用无量纲的能量参数进行解释，当时涡环发生夹止。Krueger［19］等人在以后的研究中进一步修正Slug模型，研究涡环的能量、动量和环量的来源，并研究涡环的形成过程中产生的非定常力。

在本文计算验证的部分以涡环的环量变化趋势与实验对比，在此主要讨论涡环的能量分配和动量的变化。Akhmetov［14］在解释在同一介质中，涡环的前进距离是涡环同质量同大小同传输速度下刚体的很多倍这种现象时，把涡环的能量分为传输能和涡旋能。进一步分析得出涡环的传输能只占涡环总能量大约1／3，本文进一步分析不同形成时间下涡环的总能量与传输能，如图14。随着形成时间的增加，涡环的传输速度和体积都在不断增大，所以总能量和传输能量也在增大，而进一步分析传输能所占的比例如见图15。

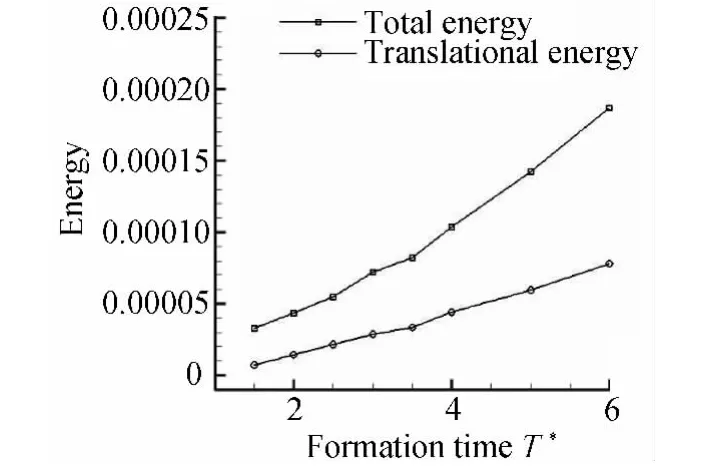
图14 不同的形成时间涡环的能量分配Fig.14 The energy distribution of vortex ring with different formation time

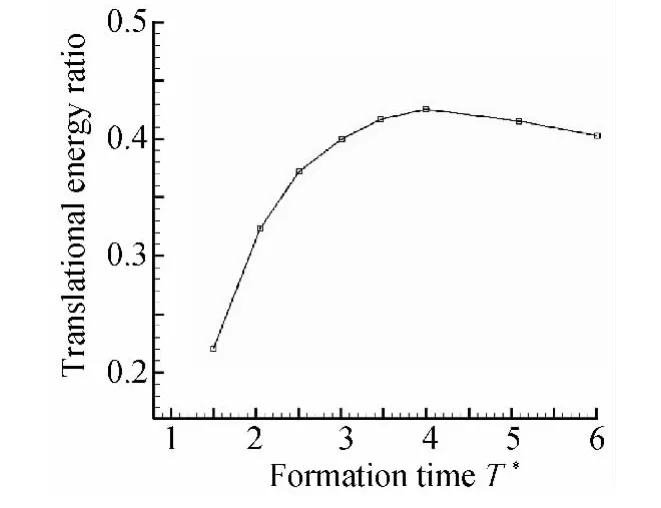
图15 不同形成时间涡环的传输能所占比例Fig.15 The translational energy ratio of vortex ring with different formation time

从图15可以看出涡环的传输能在总能量中所占比例较小。在形成时间较小时涡环的传输能所占的比例不断增大，而当涡环发生夹止后，传输能所占的比例不再上升。

从涡环的能量分配可以看出，涡环的涡旋能占据着很重要的一部分，进一步根据公式（3）和（4）计算涡环在一个形成过程中的动量及其产生的瞬时力如图16。从冲量的曲线可以看出，在涡环不断形成过程中，其冲量类似线性的不断增长。而由于涡环的冲量变化产生的瞬时力近似一个常值，而也可以看出在由于涡环的夹止对涡环产生的瞬时力产生一定的影响。

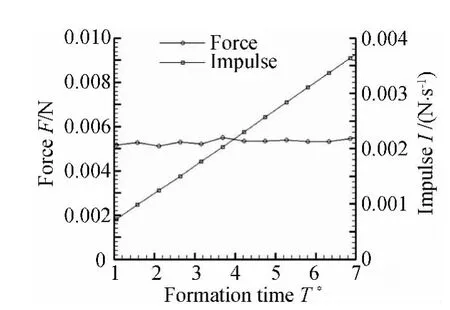
图16 涡环演化过程的冲量及瞬时力的变化Fig.16 The changes of impulse and instantaneous force in the evolution of vortex rings

3 结 论

本文通过数值模拟计算不同形成时间下涡环的形成和传输过程，并基于随体坐标系采用流函数方法确定涡环的边界及其涡环半径、涡核半径、能量等物理特征，然后与 Gharib［15］、Dabiri［8］、Akhmetov［14］等人的实验对比，说明基于流函数的方法确定涡核的边界以及确定其它物理特征是一种合理和有效的方法。

根据Gharib［15］的实验和本文的计算结果确定在该活塞的推动速度下，涡环发生夹止的形成时间在4左右。根据流函数方法确定涡环的边界可以看出，在形成时间为5时涡环已经形成出尾迹，进一步分析涡环的夹止对涡环物理特征的影响。

涡环的形成过程是流体不断进入和夹带的过程，不同形成时间下涡环夹带流体的能力不同，在形成时间在4左右时出现极小值，而后由于尾迹中出现小涡环而使夹带能力提高。同时形成时间较小的涡环（即没还有发生夹止）的一些物理参数（涡环半径R＊、涡核半径a＊、无量纲涡核半径ε）随形成时间类似线性增长，当形成时间大于4之后，涡核半径不再明显的增大，而涡环半径会进一步增大，说明涡环的夹止也意味着涡核的夹止。

把涡环的能量分为传输能和涡旋能，其中传输能只占总能量的较小一部分，并且在形成时间较小时，随着形成时间的增大涡环的传输能所占的比例在增大，而当形成时间大于4后，涡环的传输能所占比例不再进一步增大。进一步根据冲量定理和Saffman［19］对流体冲量的定义，分析涡环形成过程中瞬时力的变化。由于活塞在该速度函数下，根据Slug模型和计算结果可知，涡环的动量类似线性的增长，所以其产生的瞬时力近似一个常值。

［1］SHARIFF K，LEONARD Anthony.Vortex rings［J］.Annu.Rve.FluidMech.，1992，24：235－79.

［2］DABIRI J O.Optimal vortex formation as a unifying principle in biological propulsion［J］.Annu.Rve.FluidMech.，2009，41：17－33.

［3］DICKINSON M H.Unsteadymechanism of force generation in aquatic and aerial locomotion［J］.Amer.Zool，1996，36：537－554.

［4］DICKINSON M H.How to walk on water［J］.Nature，2003，424.

［5］FISH F E，LAUDER G V.Passive and active flow control by swimming fishes and mammals［J］.Annu.Rev.FluidMech.，2006，38：193－224.

［6］RUIZ L A，WHITTLESEY R，DABIRI J O.Vortex－enhanced propulsion［J］.J.FluidMech.，2011，668：5－32.

［7］MAXWORTHY T.Some experimental studies of vortex rings［J］.J.FuidsMech.，1977，81：465－495.

［8］DABIRI J O，GHARIB M.Fluid entrainment by isolated vortex rings［J］.J.FluidMech.，2004，511：311－331.

［9］OLCAY A B，KRUGER P S.Measurement of ambient fluid entrainment during laminar vortex ring formation［J］.Exp.Fluid，2008，44：235－247.

［10］FRAENKEL L E.Examples of steady vortex ring of small crosssection in an ideal fuild［J］.J.FluidMech.，1972，51：119－135.

［11］SAFFMAN P G.Dynamics of vorticity［J］.J.FluidMech.，1981，106：49－58.

［12］SULLIVAN I S，NIEMELA J J，HERSHBERGER R E，et al.Dynamics of thin vortex rings［J］.J.FluidMech.，2008，609：319－347.

［13］DIDDEN N.On the formation of vortex rings：rolling－up and production of circulation［J］.JournalofAppliedMathematics andPhysics，1979，30：101－116.

［14］AKHMETOV D G.Vortex rings［M］.2009.

［15］GHARIB M，RAMBOD E，SHARIFF K.A universal time scale for vorter ring formation［J］.J.FluidMech.，1998，360：121－140.

［16］LINDEN P F，TURNER J S.The formation of‘optimal’vortex rings，and the efficiency of propulsion devices［J］.J.Fluid Mech.，2001，427：61－72.

［17］KRUEGER P S，GHARIB M.The significance of vortex ring formation to the impulse and thrust of a starting jet［J］.Physicsof Fluids，2003，15：1271－81.

［18］DABIRI J O.On the estimation of swimming and flying forces from wake measurements［J］.TheJournalofExperimentalBiology，2005，208：3519－3532.

［19］SAFFMAN P G.Vortex dynamics［M］.Cambridge University Press.1992.

［20］SHUUSER M，GHARIB M.Energy and velocity of a forming vortex ring［J］.PhysicsofFluids，2000，12：618.

［21］AKHMETOV D G.Loss of energy during the motion of a vortex ting［J］.JournalofAppliedMechanicsandTechnical Physics，2008，49：18－22.