NSGA-II算法的改进及其在多段翼型缝道参数优化中的应用
倪昂修,张宇飞,陈海昕
(清华大学 航天航空学院,北京 100084)
0 引 言
增升装置对于飞机着陆性能具有较大影响。在着陆状态下,增升装置优化的主要目标是提高最大升力系数。三维增升装置设计需要以多段翼型作为基础,因此多段翼型的设计也具有较为重要的参考意义。本文为了发展集群优化平台,采用多段翼型的缝道参数优化作为背景问题,开展NSGA-II遗传算法的研究。对于增升装置设计而言,由于存在较为严重的激波/附面层干扰、尾迹/附面层干扰和不同部件的尾迹融合的现象,流动现象十分复杂。并且由于设计点接近失速状态,加之多段翼型几何复杂,更提高了CFD分析的难度。由于流动现象的复杂性,给传统的“试错法”进行增升装置设计带来了较大的难度[1]。使用计算机优化算法作为统筹,逐步改进设计方案,并进行大量的构型验证,可以给增升装置的气动设计提供较大帮助。
优化算法主要分为局部算法和全局算法两大类。局部方法的常见过程是:选取一定的初始设计点,通过计算目标函数相对于几何参数的局部导数,或者建立局部的代理模型,以确定设计参数的改变方向,随后对几何参数进行小范围变动,反复迭代直到收敛。现在应用较多的局部算法有单纯形(SIMPLEX)方法,置信域方法和伴随方法。局部算法收敛速度较快,但容易收敛到局部最优解,不易获得全局最优解。在目标函数较为复杂的情况下(增升装置气动设计就是一例),设计目标往往具有多个局部最优值,此时使用局部方法就显得不太合适。尤其是在初始设计阶段,更需要避免过早地收敛到局部最优解。而全局优化算法在寻找全局最优解方面更有优势。全局方法有很多种,较常见的例如响应面方法[2]和启发式方法。
遗传算法是一种全局优化算法,是20世纪70年代由斯坦福大学Holland教授[3]所提出的一种启发式算法。这是一种将设计参数进行编码,模仿自然界中的基因对编码进行选择、交叉、变异等操作,从而模拟自然界中对基因的优胜劣汰,最终得到表现较优的设计参数。相比于局部算法,遗传算法有更好的全局寻优的能力。另外,遗传算法是一种基于群体的启发式算法,它自然地拥有较好的并行计算潜力。本文使用的遗传算法为Deb等人提出的NSGA-II[4]。其他应用较为广泛的遗传算法有 MOGA-II[5]等等。
在气动设计中,学者们使用不同的优化算法对多种问题进行了尝试。比如Duvigneau和Visonneau使用SIMPLEX方法优化二维翼型[6];Epstein和Peigin以置信域方法作为基础发展了气动优化平台[7];Jameson将伴随方法引入平面势流方程[8],Euler方程[9]和 N-S方程[10]的求解,并且发展了相应的气动优化方法[11];国内韩忠华对Kriging代理模型的理论和应用做了较为深入的研究[12-13];陈海昕将遗传算法应用于多段翼型设计[14],王晓鹏也在博士论文中对遗传算法在气动设计中的应用进行了研究[15];白俊强等人利用Kriging算法结合粒子群算法进行了气动外形优化设计[16];等等。学者们的研究目标就在于不断提高优化算法的寻优能力,以及检验不同的优化算法的实际效用。这正是本文的两个主要目标。
随着计算机硬件的不断发展,大规模并行集群已经成为科学计算的基本工具。在优化软件平台开发过程中,实现大规模集群运算能力,并提高并行效率,也是一项重要任务。
本文的主要研究内容为:对NSGA-Ⅱ算法做一定的调整,从而在一定程度上提高其寻优能力;开发适用于气动优化设计的大规模并行优化平台;采用多段翼型优化算例,对优化平台进行验证和比较。
1 基于NSGA-Ⅱ的优化平台实现
1.1 遗传算法NSGA-Ⅱ
NSGA-Ⅱ是一种以非支配形式的排序方式实现多目标优化的遗传算法。支配关系是指在多目标优化问题中对样本进行排序时,若一个个体在所有目标上都优于另外一个个体,则称该个体支配了另外一个个体。根据这种支配关系,将某一代群体中所有未被支配的个体记为排序1(rank 1);将排序1的所有个体除去后,剩余的个体中未被支配的个体记为排序2;依此类推,这就是非支配排序方法。通过非支配排序,可以得到群体的帕雷托(Pareto)前沿。
除非支配排序方法外,NSGA-Ⅱ遗传算法在排序时,还同时考虑了约束条件和样本的拥挤距离。拥挤距离即该个体与最近的其他个体在样本空间中的距离。保留拥挤距离较大的个体有助于保持群体中的个体多样性。在竞争选择和对联合种群进行排序的环节中,每当选取两个个体进行比较时,首先考虑是否满足约束,然后考虑支配关系,最后考虑拥挤距离。这种排序方法不使用罚函数,避免了罚函数方法中系数选取的困难。
1.2 对NSGA-Ⅱ的改进
在原始的NSGA-Ⅱ算法[4]中,直接将父代种群和子代种群放置在一起,构成联合种群进行排序,从而获得新的种群。这种做法虽然加快了收敛速度,但导致实际优化过程中每一代可能只有少量新个体进入,从而使算法容易收敛到局部解。这种方式对于变量数目多,而种群规模小的优化过程十分不利。对于气动优化而言,由于每个构型的NS方程计算耗时较多,甚至每个个体都需要采用多个计算节点进行并行计算,种群规模往往无法取得较大。而气动外形的设计变量很多。为了能够更好地进行全局寻优,本文对原始NSGA-Ⅱ算法进行了修改,在算法中额外设置了一个从父代种群中挑选精英种群的过程,由精英种群代替原始方法中的父代种群,与子代种群构成联合种群,然后对其进行排序、选择、交叉和变异等操作。这样当精英种群规模相对较小时,就能既使父代种群中的优秀个体得以保存,保持了NSGA-Ⅱ的精英机制,又能够有效增加每代中的新个体数目,从而避免陷入局部优化解。改进后的算法流程参见图1。

图1 改进的NSGA-Ⅱ算法流程图Fig.1 The flowchart of improved NSGA-Ⅱ
1.3 并行集群优化架构
基于NS方程的流场求解需要消耗大量的计算资源,这要求优化平台能够实现大规模的并行优化。相比于NS方程求解而言,遗传算法本身占用的时间较少。故为了简化优化平台的并行化过程,本文仅在CFD分析上实现并行化。一台并行计算机有多个节点,每个节点可以运行多个进程,每个子进程负责运行一个完整的CFD计算。
在优化平台运行的本地计算机上采用OpenMP方法并行发布多个任务要求,通过后台控制启动远程计算机上的各个子进程,采用文件控制实现本机和并行机的通信,在完成CFD分析后,将结果返回本地计算机,然后进行适应度函数计算。以新产生的子代群体中的一个个体为例,任务发布和分析的流程示意图如图2。
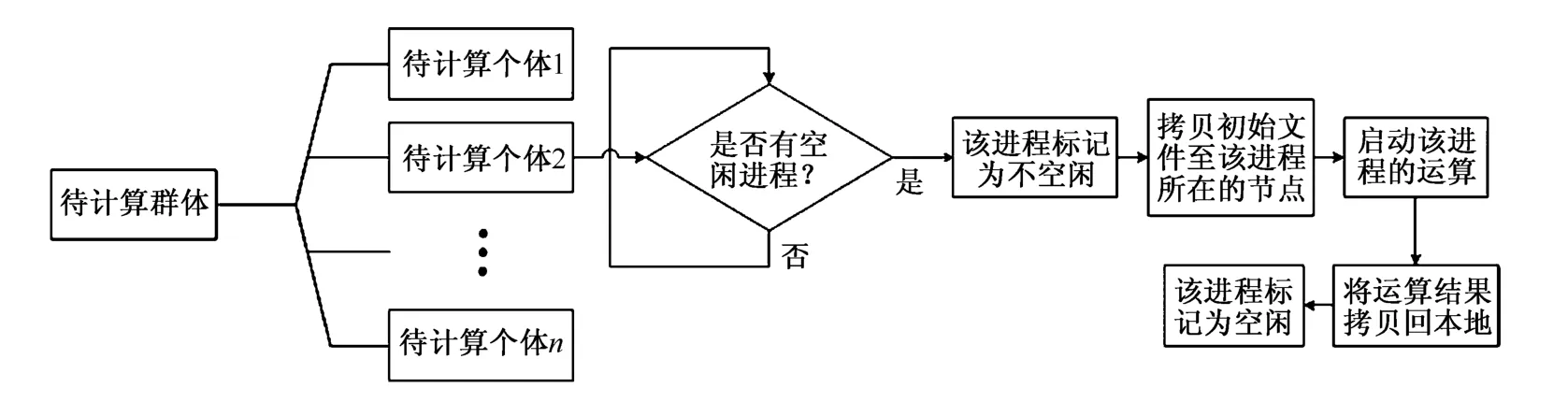
图2 并行任务发布流程示意图Fig.2 Parallel task distributing
1.4 精英种群大小的确定
本文选取了一个有理论解的问题,以寻找最佳的精英种群大小。因为随后计算的缝道参数优化问题有6个设计变量,故选取相同数目设计变量的测试问题。这里设计变量为(x1,x2,…,x6),目标函数为如式(1)所示,优化目标为求其最大值。
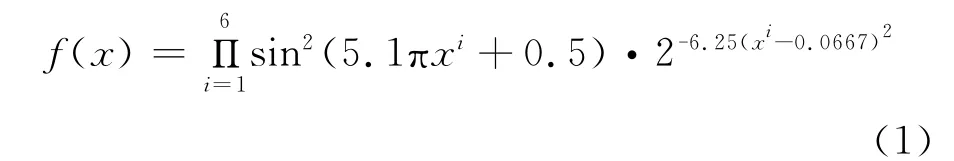
其中设计变量的范围为:
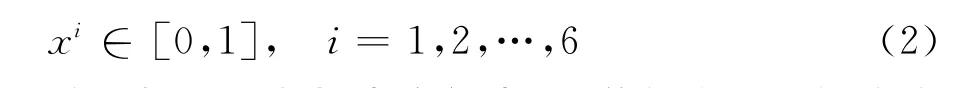
该目标函数在样本空间中,沿着每个变量的维度方向都有5个局部极大值,全局共有大约56=15625个局部极大值,而只有一个全局最优解。该目标函数的全 局最优值出现的位置是(x1,x2,…,x6)=(0.0667,…,0.0667),最优值为1.0000。
为了与后文的实际算例相匹配设置改进后的遗传算法中每代个数为44,共计24代,变异率为0.01。设定精英比为0~1,步长间隔为0.2。因为遗传算法有一定的随机性,每个精英比下求解优化问题10次。每个精英比下求得的最优值的统计结果如表1中所示。
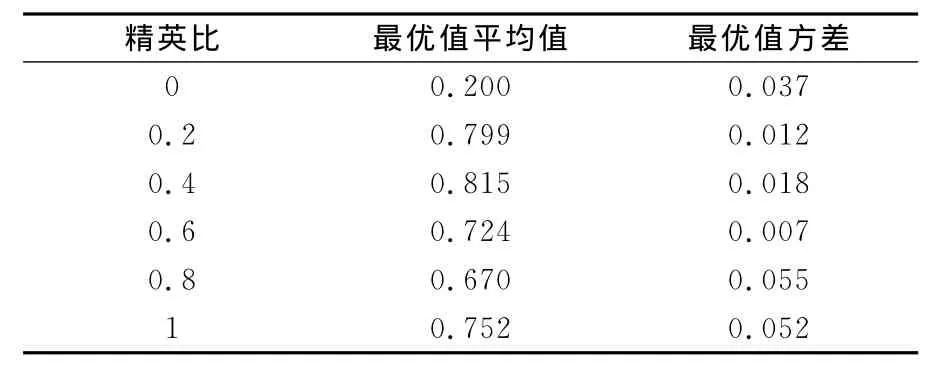
表1 精英比和计算结果之间的关系Table 1 Relationship between elite ratio and result
可以看出,精英比为0.2~0.4时,计算结果的平均值最高而方差较小。这说明取这样的精英比可以使得优化结果较好。故后文中一律取精英比为0.3。
1.5 改进后的NSGA-Ⅱ算法和其他算法的对比
使用改进后算法和原始的NSGA-Ⅱ算法,MOGA-Ⅱ算法以及单纯形(SIMPLEX)算法进行对比。其中MOGA-Ⅱ是一种使用较为广泛的遗传算法;而单纯形算法是一种局部算法。
用这些方法求解式(1)的优化问题,此时取sin函数的6次方,从而进一步加大了优化难度。改进后的NSGA-Ⅱ算法中,设置精英种群的大小为父代种群大小的约0.3倍:在本算例中,父代种群每代有44个个体,精英种群有13个个体。在其他参数上,改进后算法和原始的NSGA-Ⅱ算法以及 MOGA-Ⅱ算法使用同样的设置。因改进后的算法在进行140代迭代计算后即寻找到全局最优,故其他两种遗传算法也设置为进行140代计算。使用各种算法的计算收敛过程如图3所示。
从图3可以看到,经过同样代数的计算,改进后的NSGA-Ⅱ算法是唯一一个寻找到全局最优的算法。而原始的的NSGA-Ⅱ算法和MOGA-Ⅱ算法不仅未能寻找到全局最优,而且在优化的过程中出现了“平台”,即最优个体的目标函数停留在一定数值长时间没有改善——这种情况在实际的优化过程中会被误认为是优化过程已经收敛。可以看到,通过上文提到的改进,NSGA-Ⅱ算法的确有了更好的全局寻优能力。
而局部算法SIMPLEX在进行150次左右计算之后,就收敛到了局部最优。在优化的初期,SIMPLEX算法的目标函数提升比改进的NSGA-Ⅱ算法更快,随着迭代过程的进行,SIMPLEX算法很快收敛,但是此时其结果距离全局最优还有很大的差距。相比之下,改进后的NSGA-Ⅱ算法虽然收敛比较慢,但能够得到全局最优解。
对于气动优化而言,几何外形的设计变量较多,解空间非常有可能存在多个局部最优值。使用局部优化算法虽然能够较快收敛,并且也能获得性能的改善,但是得到的结果可能距离全局最优具有较大的差距。为了充分提高设计的气动性能,避免在设计初期就陷于局部最优解,加强优化算法的全局寻优能力十分重要。

图3 改进后的NSGA-Ⅱ,原始的NSGA-Ⅱ,MOGA-Ⅱ,SIMPLEX算法的目标函数收敛历史Fig.3 The history plot of fitness function of the result of improved NSGA-Ⅱ,original NSGA-Ⅱ,MOGA-Ⅱ,and SIMPLEX algorithm
2 多段翼型缝道参数优化设计
2.1 问题描述
对于民用飞机的增升装置而言,着陆构型应当尽量提高其最大升力系数,并且最大升力系数之后失速特性应较为缓和。故本文选择临近失速的攻角作为优化设计状态[1,14]。马赫数设为0.2,雷诺数5×106。优化目标为攻角18°时升力系数最大。
多段翼型的构型包括缝翼、主翼和襟翼,各部分翼型定义见图4。
缝道参数优化的设计变量包括前缘缝翼和后缘襟翼的搭接量(用弦长无量纲化)、缝隙宽度(用弦长无量纲化)和偏角共计6个参数[14],如图5所示。各设计变量的范围变化范围见表2。
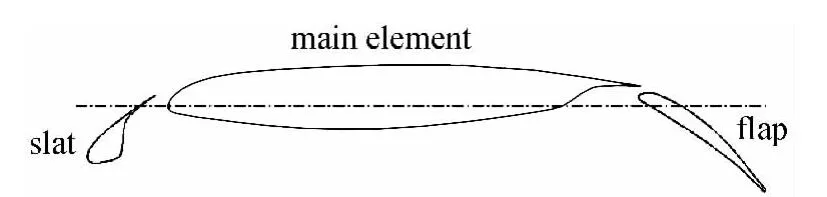
图4 各部分翼型定义Fig.4 Multi-element definition

图5 设计参数定义Fig.5 Definition of design parameters

表2 设计变量范围Table 2 Parameter range
2.2 计算方法验证
文献[17]对多段翼型进行了风洞实验。在马赫数为0.197的条件下,进行了攻角为4°和20.18°的两组实验,雷诺数为3.52×106。从中选取和本文研究对象最为接近的三段翼型作为算例,验证将要使用的计算方法。计算使用的网格为单块网格,网格点总数约5万,采用的湍流模式是两方程SST模式。计算网格如图6所示。CFD求得的压力分布和实验结果对比如图7所示。可以看出,该网格与NS方程求解器组合可保证CFD分析具有足够的精度以及对多段翼型流动中复杂气动现象的解析能力。可以用于开展后续的设计工作。

图6 三段翼型网格Fig.6 Grid of 3-element airfoil
2.3 多段翼型优化设计结果
采用2.2中验证过的气动分析方法,同样拓扑结构和密度的网格,结合改进的NSGA-Ⅱ算法开展多段翼型缝道参数优化。设置遗传算法每代为44个个体,一共迭代24代(初始种群记为第一代),设置精英种群大小为13个个体。在给定各设计参数之后,由脚本控制完成网格自动化生成。进行数值计算得到翼型升力阻力。针对某些缝道参数位置可能出现的CFD计算不收敛的情况,结合迭代步数和收敛历史判断剔除不合理的结果。

图7 α=4°和α=20.18°时压力系数实验与计算对比(从上至下)Fig.7 Comparison of Cp between experiments and CFD atα=4°and 20.18°(from top to bottom)
计算采用5台8核2.4GHz和1台4核2.7GHz的刀片机节点进行并行计算,运行20小时后得到多段翼型的优化结果。目标函数升力系数的收敛历史见图8。初代种群的最优个体编号为15,将其视为初始方案;优化获得的最终最优个体编号为897,即20代的第17个个体。
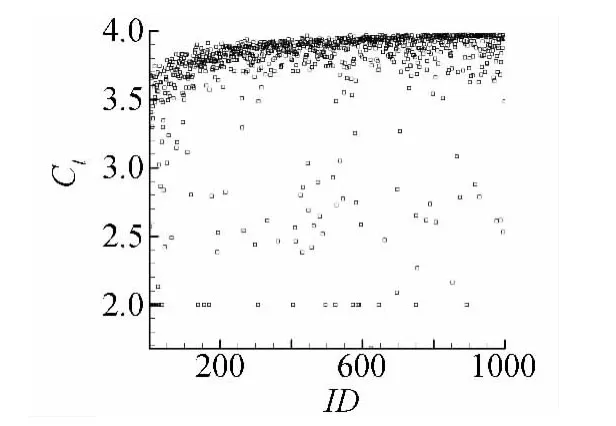
图8 目标函数历史图Fig.8 The history plot of fitness function
初代种群的最优个体(ID:15)和最终最优个体(ID:897)的CFD分析的升力系数收敛历史和表面压力系数对比见图9和图10。经过遗传算法24代的迭代后,升力系数从最开始的3.75提升到了大约3.97。最终最优个体压力分布形态合理,主翼与襟翼上的环量有明显提高,吸力峰值有适度增长,襟翼上的分离得到一定的抑制。
将本文提出的改进后的算法的结果,和原始NSGA-Ⅱ算法的结果做一对比。对原始的NSGA-Ⅱ优化算法,设置同样的种群规模和初始值,进行相同多段翼型的优化,两种方法优化结果对比如表3所示。从表3中可以看到,所得最佳个体升力系数相近,缝道参数区别不大,尤其是对升力系数起重要作用的缝翼和襟翼偏角几乎完全一样。但是原始的NSGA-Ⅱ算法的最佳个体获得经过了更多的迭代代数,所需的时间稍长。从优化结果和过程来看,改进后的NSGA-Ⅱ算法在实际问题中具有优秀的性能;自行开发的优化平台软件运行效果良好。后续将在此平台上进一步对优化算法进行发展。

图9 初始方案与优化方案CFD升力系数收敛历史图Fig.9 Clhistory plot of initial design and best design
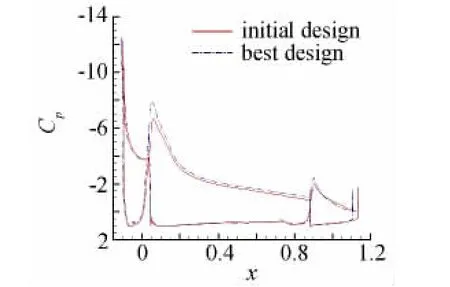
图10 初始方案与优化方案压力系数图Fig.10 Cpplot of initial design and best design

表3 与原始NSGA-Ⅱ算法的设计结果对比Table 3 Comparison of design result with original NSGA-Ⅱ
3 结 论
本文提出在NSGA-Ⅱ算法中,对加入新种群的父代种群个体进行精英筛选,从而增加新种群中新个体的数目。改进后的NSGA-Ⅱ算法具有明显改进的全局寻优能力。
采用改进后的NSGA-Ⅱ算法对多段翼型的缝道参数进行了优化。经过每代44个个体共计24代迭代运算后,翼型升力系数提高约0.22。与原始NSGA-Ⅱ算法的结果对比,最优个体的性能相当,改进后的算法寻优速度加快。后续将在自行开发的平台上进一步开展优化算法的改进。
[1]张宇飞,基于先进CFD方法的民用客机气动优化设计[D].[博士论文].北京:清华大学,2010.
[2]JONES D R.A taxonomy of global optimization methods based on response surfaces[J].JournalofGlobalOptimization,2001,21(4):345-383.
[3]HOLLAND J H.Adaptation in natural and artificial systems:an introductory analysis with applications to biology,control and artificial intelligence[M].MIT Press,1992.
[4]DEB K.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].EvolutionaryComputation,IEEETransactionson,2002,6(2):182-197.
[5]POLES S.MOGA-Ⅱan improved multi-objective genetic algorithm[R].Trieste.ESTECO Technical Report 6,2003.
[6]DUVIGNEAU R,VISONNEAU M.Shape optimization of incompressible and turbulent flows using the simplex method[C].15th AIAA Computational Fluid Dynamics Conference,Anaheim,CA,2001.
[7]EPSTEIN B,PEIGIN S.Robust hybrid approach to multiobjective constrained optimization in aerodynamics[J].AIAAJour-nal,2004,42(8):1572-1581.
[8]JAMESON A.Aerodynamic design via control theory[J].JournalofScientificComputing,1988,3(3):233-260.
[9]REUTHE J,JAMESON A.Control theory based airfoil design using the Euler equations[R].AIAA Paper,1994:206-222.
[10]JAMESON A,MARTINELLI L,PIERCE N,Optimum aerodynamic design using the Navier-Stokes equations[J].TheoreticalandComputationalFluidDynamics,1998,10:213-237.
[11]MARTINELLI L,JAMESON A.Computational aerodynamics:solvers and shape optimization[J].JournalofHeatTransfer,2013,135(1)011002:1-9.
[12]HAN Z H,ZIMMERMAN R,GÖRTZ S.Alternative cokriging method for variable-fidelity surrogate modeling[J].AIAAJournal,2012,50(5):1205-1210.
[13]HAN Z H,GÖRTZ S.Hierarchical kriging model for variablefidelity surrogate modeling[J].AIAAJournal,2012,50(9):1885-1896.
[14]CHEN H X,ZHANG Y F,ZHANG W S,et al.GA optimization design of multi-element airfoil[C].ICCFD7.Big Island,Hawaii,USA,2012.
[15]王晓鹏.遗传算法及其在气动优化设计中的应用研究[D].[博士论文].西安:西北工业大学,2000.
[16]白俊强,王波,孙智伟,等.基于松散式代理模型管理框架的亚音速机翼优化设计方法研究[J].西北工业大学学报,2011(04):515-519.
[17]VALAREZO W O,DOMINIK C J,MCGHEE R J,et al.Multi-element airfoil optimization for maximum lift at high Reynolds numbers[R].AIAA-91-3332.9th AIAA Applied Aerodynamics Conference,Volume 2,1991:969-976.

