基于气动力分段表达的颤振求解方法与模态跟踪技术的应用

任智毅，金海波，丁运亮

（1.上海航天技术研究院 第八设计部，上海 201109；2.南京航空航天大学 航空宇航学院，南京 210016）

0 引 言

颤振是一种典型的气动弹性动不稳定现象，气动弹性的运动方程通过振型线性化假设、模态降阶等理论将其转换成质量归一化的广义结构运动方程，通过求解该方程的非线性二次特征值问题来确定结构颤振的临界稳定条件。目前大多数颤振分析方法求解其特征根都需要在指定的折合频率区间上进行广义气动力的插值和不断迭代两个过程［1－2］。由于采用迭代的方法求解颤振方程不仅增加计算时间而且可能存在收敛性问题，因此Goodman［3］提出了一种不需要迭代的颤振求解方法即采用n个折合频率将折合频率区间分成n－1段，并通过分段插值函数（PQI）来近似表达广义气动力与折合频率之间的函数关系，从而将颤振方程的求解转化为分段线性二次特征值问题。由于Goodman在分段边界上只进行了前后分段插值函数的广义气动力匹配，没有保证段与段之间插值函数一阶导数的连续性，导致特征根在分段边界上出现间断和重叠现象，从而发生模态窜支。Eller［4］在此基础上采用n－1个折合频率将折合频率区间分成n－2段，在分段边界上增加了前后分段插值函数的一阶导数连续性条件，从而保证了颤振方程特征根的连续性，因此Eller认为该方法在颤振计算过程中不会出现模态窜支现象，故不需要模态跟踪。但是由于分段插值函数的构建依赖于折合频率的选择，将构造的插值函数嵌入颤振方程计算过程中仍然会产生模态窜支现象，其原因主要是在颤振方程分段求解中，在同一插值段内可能获得其中两支或者更多模态的特征根，由于在该段颤振方程特征值的计算中这些特征根是没有顺序的，从而出现各阶模态对应的特征值随参数变化的前后对应关系混乱即“模态交叉”现象，如果不采用有效的模态跟踪技术来跟踪这些特征根，这将给颤振模态识别带来困难。

对于模态跟踪技术，目前主要采用相似排序法［5］、正交检验法［6］、预测跟踪法［7］等。由于相似排序法和正交检验法需要较小的步长，其参数变化前后特征值的相似性和特征向量的正交性条件才近似成立，且对于复杂的系统可能出现模态跟踪失败现象，因此本文针对颤振求解PQI法，发展了一种基于特征值摄动理论的模态跟踪技术－预测跟踪法，它利用特征值及左、右特征向量信息求解下一参数点的特征值估计量，以估计量为参考来跟踪模态的变化情况，解决了其存在的模态窜支问题。

本文介绍了带有模态跟踪的PQI颤振分析的基本方法，并用两个标准算例验证了该方法的计算精度和有效性。

1 颤振方程的直接求解方法

1.1 颤振的运动方程

在小变形和线弹性材料假设前提下，通过拉普拉斯变换将颤振分析的运动方程写成式（1）［8］：

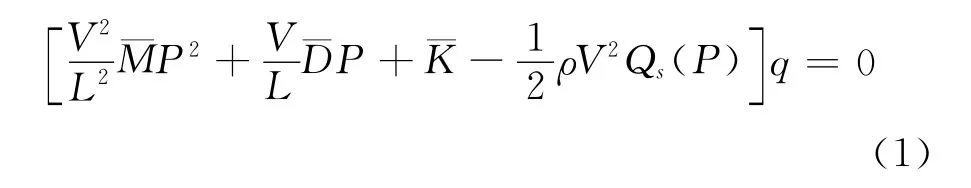
式中是广义质量矩阵，是广义阻尼矩阵，V是来流速度，L是参考弦长的一半，ρ是大气密度；Qs（P）是拉普拉斯域广义气动力矩阵，P是拉普拉斯参数，P＝g＋ik，g是阻尼，k为折合频率，k＝ωL／V，ω为结构的固有频率。

在常规的颤振方程（1）的求解中，由于气动力Qs（P）矩阵是关于P的非线性非对称矩阵，所以需要采用一种迭代的方法求解非线性矩阵特征值问题的特征根，一般的做法是给定，计算其对应的气动力Q（），并结合寻优的过程来寻找线性特征值问题的解中与相等的特征根P即为非线性特征值问题式（1）的解。

本文拟采用分段表达的方式把气动力Qs（P）矩阵表示为关于p的二次表达形式，如式（2）：

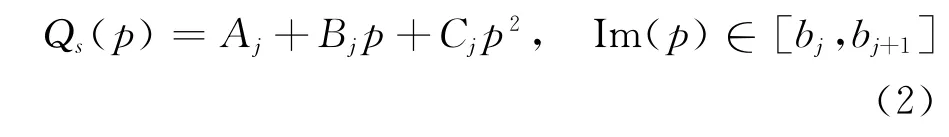
式中A、B、C是多项式的非对称系数矩阵，j是分段数，b为折合频率区间分段断点。

采用这样的表达方式，其优点在于：① 采用这样的表达将颤振方程（1）的非线性特征值问题转化为分段线性特征值问题；② 由于式（2）满足柯西－黎曼方程（3）［9］，因此整个复平面的分段二次气动力插值函数可以仅仅沿着虚轴来构建，同时可以看出采用二次插值函数对阻尼的变化进行了二阶近似，由于气动力是在复平面上构造的，因此其气动阻尼的计算更为精确。

虽然采用二次形式可以解决复平面气动力矩阵的近似表达问题，但由于颤振计算中非定常气动力的非线性特性，因此本文采用分段形式来提高近似表达精度，在分段表达中本文采用的分段方法为：首先在折合频率求解空间构造一系列离散点ki（i∈［1，n］），并在该离散点上计算所对应的广义气动力Q（iki），然后分段插值函数的断点位置bj（j∈［1，n－1］）按如下原则构造：

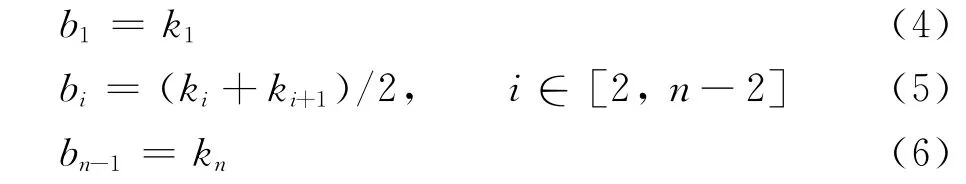
对于每一折合频率分段j（k∈［bj，bj＋1］），满足三个条件：如式（7）的断点连续性；式（8）的断点符合性；式（9）的断点处分段函数一阶导数连续性：

其中第一段与最后一段条件需要做适当的修改，即在第一段的三个条件中将式（7）改为式（10），最后一段中将式（9）改为式（11）：

这样处理使得每一折合频率分段都满足三个条件，由于段与段之间的条件是相互联系的，通过分块组集的方法将其整合成矩阵的形式，通过矩阵变换来直接求解分段系数矩阵（Ah×h）j、（Bh×h）j、（Ch×h）j，h表示参与颤振分析的模态数量。以第一段和最后一段的系数求解为例：

式中（Ats）j、（Bts）j、（Cts）j表示第j段三个系数矩阵中的t行s列元素（t，s∈［1，h］），（Qts）kj表示折合频率ki所对应的广义气动力的Q（iki）的t行s列元素（i∈［1，n］）。

1.2 颤振方程的求解

将式（1）与式（2）整合在一起，颤振方程可改写为式（13）：

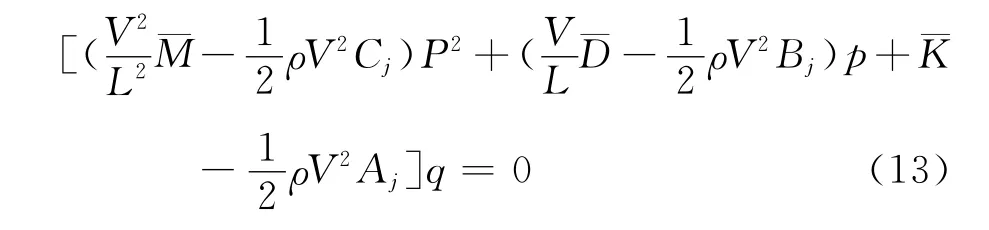
式（13）的求解可以通过引入状态变量的方法［10］进行求解：

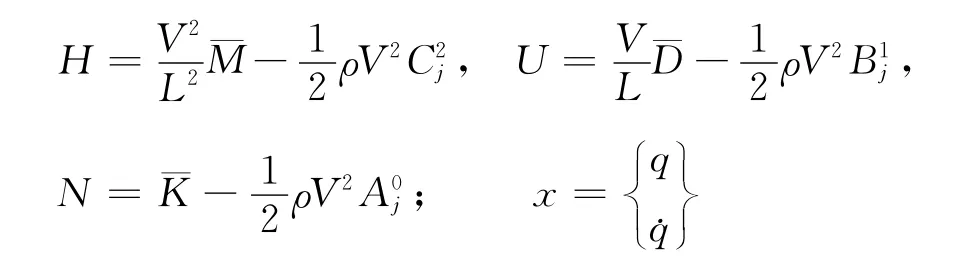
由于式（13）中气动力Qj（P）是分段近似表达的，对于第j段，按式（14）求解特征值P。由于气动力仅在j段内有效，因此需要判断特征根是否在该求解段上即条件Im（p）∈［bj，bj＋1］。如果在，其求解有效，如果不在，则需要用下一求解段继续求解，通过逐段求解的方式可以找出式（1）在给定V下所对应的参与颤振分析的各阶模态的特征值。但是在用分段气动力对其近似求解时，对于同一给定V条件，可能多支参与颤振分析的模态的特征根落在同一分段上，在该段上这些有效特征根与前一空速相应模态的对应关系无法确定，这时需要采用模态跟踪法对其进行跟踪。本文的特征值跟踪方式为：在某一空速Vm下，采用上述方法获取参与颤振分析的各阶模态的对应的特征根及其对应的有效分段区间，在此基础之上，基于各阶模态在其对应的有效段上的特征根及其相应的左特征向量（）和右特征向量（），根据特征值摄动理论，来确定各阶模态在下一空速Vm＋1下对应的预测特征值如式（15），以预测值为参考对进行排序。

特征值的对应关系确定如下：在空速Vm下，求解空速Vm＋1下的预测特征值，然后从空速Vm＋1对应的特征值（j＝1，2，...，n）中找到与之对应的，使其满足式（16）。

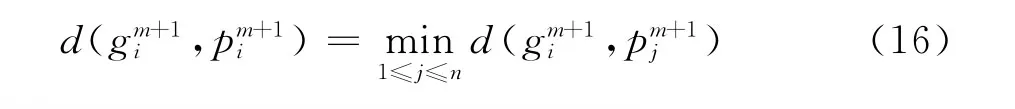
式中：

在模态的跟踪过程中，可能出现速度步长过大而导致模态跟踪失败，故给定一个阈值ε，当d（，）＞ε时，减小速度步长即将步长除以因子T（T＞1）来重新计算特征值与排序，算法流程图见图1。

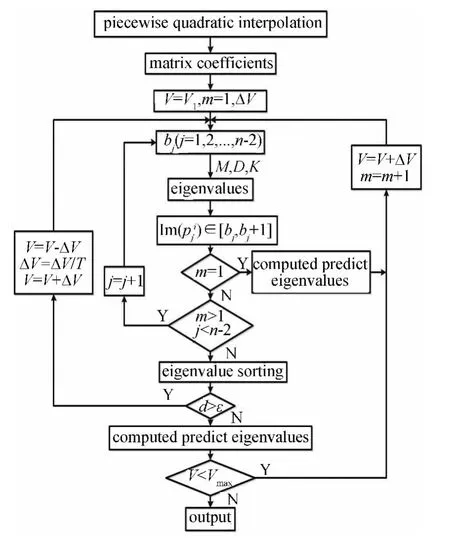
图1 带有模态跟踪的PQI法流程图Fig.1 The flow diagram of the PQI method with mode tracking

2 实例分析

2.1 数值分析一

颤振分析模型采用有限元软件MSC.NASTRAN提供的标准算例：平板机翼的后掠角为15°，飞行马赫数Ma为0.45。编写偶极子格网法程序［11－15］求解气动力影响系数矩阵，采用有限元软件MSC.NASTRAN获取结构的广义质量矩阵、广义刚度矩阵、固有频率和振型等，采用无限板样条函数［16］实现气动结构的耦合，编写PQI法程序求解结构的颤振临界速度和频率。该算例的折合频率k的区间范围为0～1，其分段区间均长0.02，共50段，空速范围是10m／s到220m／s，速度步长为5m／s，选取结构的前4阶固有模态进行颤振分析。

采用不带模态跟踪的PQI法进行颤振分析，其V－g曲线和V－f曲线见图2，模态窜支处折合频率k的计算结果见表1，其中g代表模态阻尼，f为频率。从图2和表1可以得知，在空速为60m／s时，二阶模态和三阶模态的折合频率分别为0.051、0.064，它们处在同一折合频率分段0.05～0.07上，由于在该分段上的二阶模态和三阶模态与前一空速相应的模态对应关系不明确，从而造成模态对应关系混乱，出现“模态交叉”现象。在空速为80m／s、85m／s、90m／s时，在折合频率分段0.03～0.05上发生同样情况。

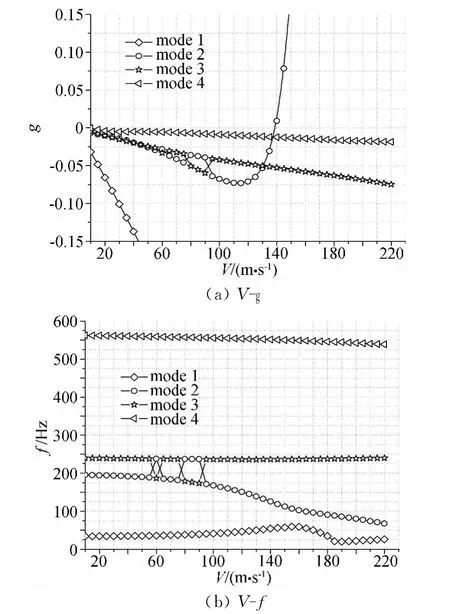
图2 不带模态跟踪的PQI法计算结果Fig.2 The solutions of PQI method without mode tracking

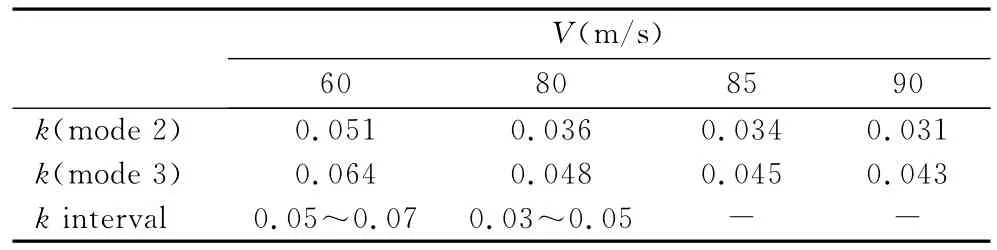
表1 模态窜支点处折合频率的计算结果Table 1 Reduced frequencies of mode tracking

采用带有模态跟踪的PQI法与工程上常用的PK法对此模型进行对比分析，两种方法求解的V－g曲线和V－f曲线见图3，从图中可以看出，对于PQI法，采用模态跟踪后，模态窜支问题得到很好的解决。此外，从图3的V－g曲线知，平板机翼模型的颤振模态为第二阶模态，该模态的阻尼曲线与g＝0的交点所对应的速度即为颤振临界速度，而两种方法获取的该支模态的阻力曲线与g＝0交点的位置几乎重合，这说明两种方法对颤振临界速度的计算精度非常接近，PQI法和P－K法计算的颤振临界速度分别为138.2m／s、140.6m／s，颤振频率分别为127.3Hz、128.8Hz。

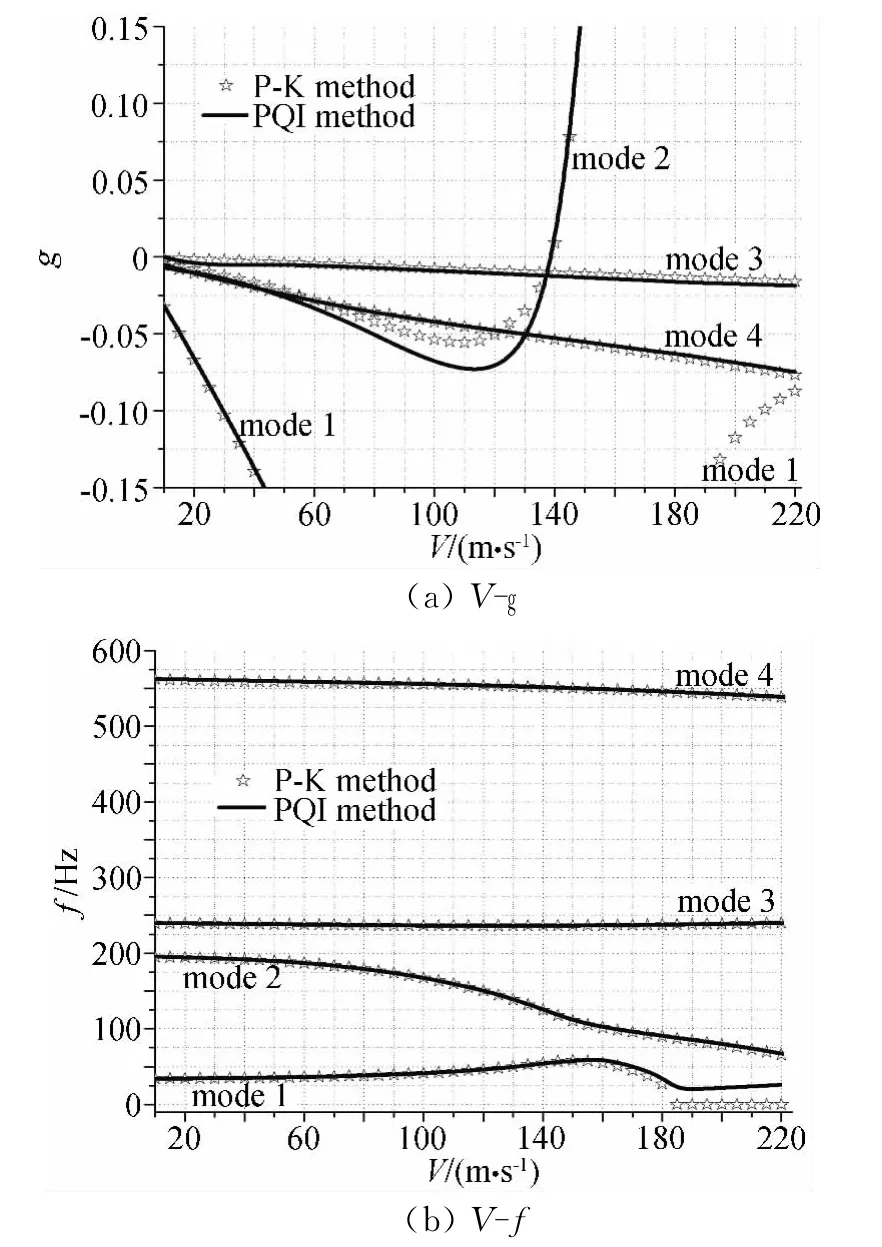
图3 带有模态跟踪的PQI法和P－K法的计算结果Fig.3 The solutions of PQI method with mode tracking and P－K method

PQI法和P－K法计算结果的不同之处在于：（1）从图3中曲线知，在空速小于185m／s时，模态阻尼在数值上略有差别，其原因是PQI法采用二次插值函数对阻尼的变化进行了二阶近似，其阻尼的计算更为精确；（2）在空速大于185m／s时，图3中V－g和V－f曲线存在较大差异，其原因是P－K法中一阶模态出现了窜支现象，获得气动滞后根即零频率根，因此该阶模态的V－g曲线不连续，而在PQI法中能够很好的跟踪该阶模态的特征根，从图3中V－f曲线中可知，在空速大于185m／s时，一阶模态的频率大于零，从而保证了该阶模态阻尼曲线的连续性，不过数值分析表明PQI法在空速185m／s到220m／s区间，该支模态其特征根p（p＝g＋ik）显示｜g｜＞k，在此大阻尼情况下，其气动力的计算是不精确的，因此该区间的计算结果是可疑的，表2给出了其中部分特征根p的信息，图4为不同阻尼情况下的广义气动力分量Q44随折合频率k的变化趋势，其中g＝0情况下的气动力是偶极子格网法程序计算结果，而g≠0情况下的气动力是通过分段气动力插值函数式（2）获取，从表2与图4可知，在大阻尼下当｜g｜＞k时，通过分段二次插值函数获取的气动力相对于小阻尼情况偏差较大。

表2 不同空速下的模态特征根Table 2 The eigenvalues of modes at different airspeeds

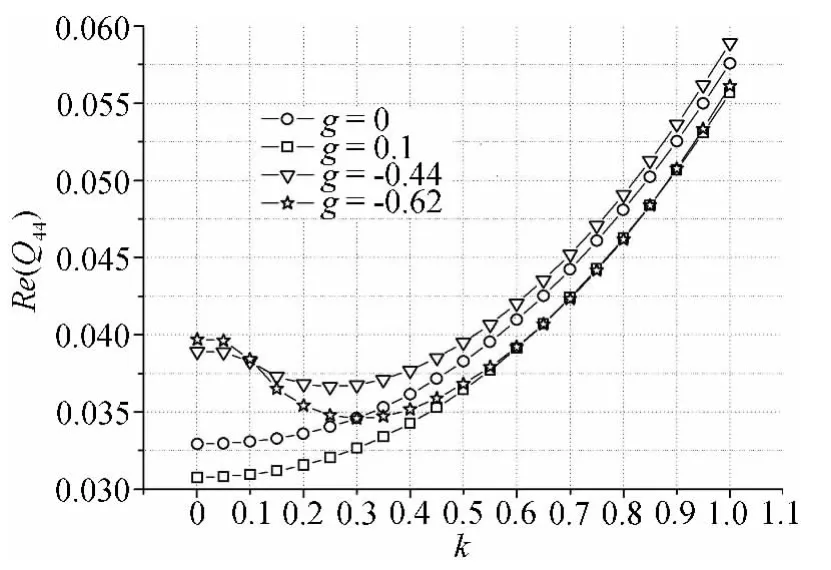
图4 不同阻尼下的插值气动力Fig.4 Interpolation evaluated at different g

2.2 飞机全机颤振分析

为了验证本文发展方法在实际工程颤振分析中的有效性，将其用在商用软件ZAERO［17］提供的F－18全机轴对称状态颤振分析中，折合频率区间范围为0.01～0.8，将其分成60分段，空速范围是120m／s到360m／s，速度步长为5m／s，选取结构的前12阶结构固有模态，采用PQI法进行颤振分析，其V－g和V－f曲线见图5，采用带有模态跟踪的PQI法分析，其V－g和V－f曲线见图6。从图5可以看出，对于复杂的结构，采用PQI方法模态窜支现象比较严重，颤振模态的识别受到干扰，采用模态跟踪法之后，图6显示其V－g曲线和V－f曲线光滑合理，其颤振速度为250.05m／s，颤振频率为23.25Hz。

图5 不带模态跟踪的PQI法的计算结果Fig.5 The solutions of the PQI method without mode tracking

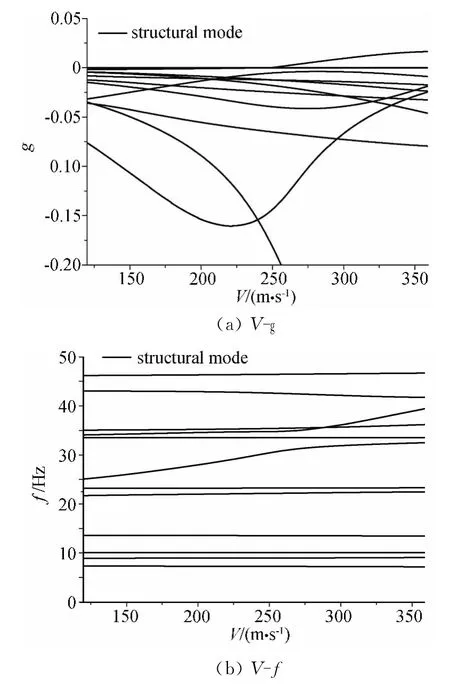
图6 带有模态跟踪的PQI法的计算结果Fig.6 The solutions of the PQI method with mode tracking

3 结 论

（1）本文针对PQI法，发展了一种基于特征值摄动理论的模态跟踪技术－预测跟踪法，解决了其存在的模态窜支问题，同时也验证了该方法在模态跟踪过程中具有良好的跟踪效果。

（2）PQI法相对于PK法的最大优势在于对广义气动力采用了分段表达的形式，从而将颤振方程求解的非线性二次特征值问题转化为分段线性二次特征值问题，即采用分段直接求解的思想，因此不需要迭代，而PK法采用迭代的方式求解颤振方程的特征根，故需要预先给出一定的收敛裕度，对于复杂的结构可能存在不收敛性。

（3）从颤振计算精度上看，PQI法与工程上常用的PK法的计算精度非常接近。

（4）从阻尼的角度看，相对于PK法，PQI法对阻尼的变化进行了二阶近似，其阻尼的计算更为精确。

［1］RODDEN W P，JOHNSON E H.MSC／Nastran v68aeroelastic analysis user′s guide［M］.Los Angeles：MSC.Software Corporation，1994：73－76.

［2］HASSIG H J.An approximate true damping solution of the flutter equation by determinant iteration［J］.JournalofAircraft，1971，8（11）：885－889.doi：10.2514／3.44311

［3］GOODMAN C.Accurate subcritical damping solution of flutter equation using piecewise aerodynamic function［J］.Journalof Aircraft，2001，38（4）：755－763.doi：10.2514／2.2828

［4］ELLER D.Flutter equation as piecewise quadratic eigenvalue problem［J］.JournalofAircraft，2009，46（3）：1068－1070.doi：10.2514／1.40653

［5］XIE C C，HU W W，YANG C.Eigenvalue sorting problem in flutter analysis［J］.MathematicsinPracticeandTheory，2007，37（18）：141－146.（in Chinese）谢长川，胡薇薇，杨超.颤振分析中的特征值排序问题［J］.数学的实践与认识，2007，37（18）：141－146.doi：10.3969／j.issn.1000－0984.2007.18.022

［6］Van ZYL L H.Use of eigenvectors in the solution of the flutter equation［J］.JournalofAircraft，1993，30（4）：553－554.doi：10.2514／3.46380

［7］CHEN P C.A damping perturbation method for flutter solution：the g－method［J］.AIAAJournal，2000，38（9）：1519－1524.doi：10.2514／2.1171

［8］GUAN D.Aeroelasticity handbook of aircraft［M］.Beijing Aeronautical Industry Press，1994：126－134.（in Chinese）管德.飞机气动弹性力学手册［M］.北京：航空工业出版社，1994：126－134.

［9］LOUIS A P.Applied mathematics for engineers and physicists［M］.New York：Mograw－Hill Book Company，1946：448－452.

［10］FANG T，XUE P.Theory of vibration with applications［M］.Xi′an：Northwestern Polytechnical University Press，1998：130－136.（in Chinese）方同，薛璞.振动理论及应用［M］.西安：西北工业大学出版社，1998：130－136.

［11］ALBANO E，RODDEN W P.A doublet－lattice method for calculating lift distributions of oscillating surfaces in subsonic flow［J］.AIAAJournal，1969，7（2）：279－285.doi：10.2514／6.1968－73

［12］RODDEN W P，GIESING J P.Refinement of the nonplanar aspects of the subsonic doublet－lattice lifting－surface method［J］.JournalofAircraft，1972，9（1）：69－73.doi：10.2514／2.2382

［13］RODDEN W P，TAYLOR P F.Further refinement of the nonplanar aspects of the subsonic doublet－lattice lifting surface method［J］.JournalofAircraft，1998，35（5）：720－727.doi：10.2514／3.44322

［14］YANG L F.A new method of flutter analysis［J］.ACTAAerodynamicaSinica，1994，12（2）：196－199.（in Chinese）杨立法.一种颤振分析新方法［J］.空气动力学学报，1994，12（2）：196－199.

［15］SUN S P，CHEN J S.Doublet point method for harmonically oscillating lifting surfaces in subsonic flow［J］.ACTAAerodynamicaSinica，1993，（1）：011.（in Chinese）孙少鹏，陈劲松.亚声速谐振升力面的点偶极子法［J］.空气动力学学报，1993，（1）：011.

［16］HARDER R L，DESMARAIS R N.Interpolation using surface splines［J］.AIAAJournal，1972，9（2）：189－191.doi：10.2514／3.44330

［17］ZONA Technology Inc.ZAERO version 7.4theoretical manual［M］.Scottsdale：ZONA Technology Inc.，2006：297－302.