地铁车站长距离密贴下穿既有隧道结构的地震响应

陶连金,　闫冬梅,　李积栋,　郭　飞,　周明科

(北京工业大学 岩土与地下工程研究所, 北京 100124)



地铁车站长距离密贴下穿既有隧道结构的地震响应

陶连金,闫冬梅,李积栋,郭飞,周明科

(北京工业大学 岩土与地下工程研究所, 北京 100124)

为研究长距离密贴下穿地下空间结构的地震响应特征,以某新建地铁车站结构长距离密贴下穿既有隧道结构为对象,基于FLAC3D有限差分软件,建立三维数值计算模型。在输入日本阪神(Kobe)地震波的条件下,分析上部既有隧道结构在有无下穿地铁车站结构时的地震响应。计算结果表明:输入水平方向的地震波,有无地铁车站结构的隧道结构的位移-时程与加速度-时程曲线规律大致相同,均随深度的增加而减小,且变化趋势相似于施加的地震波。隧道顶板与底板的加速度反应时程曲线与基岩输入地震波的形态基本相近,隧道结构顶板的水平加速度峰值大于底板的水平加速度峰值。与单一隧道结构的位移-时程和加速度-时程曲线相比,密贴地铁车站结构对隧道结构的动力响应有减弱效果。下穿地铁车站对上部隧道结构的动力加速度响应有不同程度的减弱效应,且越靠近车站结构减弱幅度越大,下部车站结构的减震耗能现象存在于某一局部范围内。

既有隧道结构; 地震响应; 地铁车站; 密贴下穿; FLAC3D有限差分法

0　引　言

近年来,随着地铁施工技术的日趋成熟及地下空间的不断开发利用,地下工程中地铁车站与隧道结构的空间组合形式越来越复杂多变,如十字形、X形的交叉和上下平行线等。以北京地区为例,新建结构与既有结构的距离也越来越近,有些甚至为0 m[1]。如地铁10号线国贸—双井站区间暗挖隧道密贴下穿既有地铁 1号线、地铁机场线东直门站密贴下穿既有地铁 13号线折返线隧道等[2]。

随着我国城市轨道交通网络日益规模化,这种密贴穿越组合结构也会越来越多,地铁车站与隧道结构相互交叉穿越,两者相互作用,相互影响。自20世纪80年代以来,相继发生的一些大地震,如1995年日本Kobe地震、2012年中国汶川地震,造成了大量的人员伤亡和建筑物的严重破坏。地铁车站与隧道结构作为交通枢纽,其抗震性能更是不可忽视。目前，国内外一些学者虽然针对地下空间组合结构的地震响应问题作了一些研究[3-7],但仍存在一些问题,如由于受数值计算条件的限制,多将三维问题简化为二维问题,这样不仅影响精度,也无法进行复杂结构的数值模拟;建立的模型形式、地层性质的假定也较为单一[8-9],对于长距离密贴结构的研究较少。随着地铁数量的不断增加,密贴穿越结构将越来越普遍,因此，研究地铁车站与隧道长距离密贴下穿结构的地震响应具有重要现实意义。

笔者基于FLAC3D有限差分软件,以某新建地铁车站结构长距离密贴下穿既有隧道结构为原型，建立三维模型。在水平输入日本阪神(Kobe)地震波的基础上,对既有隧道结构的地震响应位移及加速度进行比较分析,研究地铁水平密贴形式对既有隧道地震响应的影响规律。

1　模型建立

某新建地铁车站长距离密贴下穿既有隧道主体结构,相对位置关系见图1。上层既有隧道为两跨单层的矩形混凝土结构,高10.00 m,宽34.40 m,顶、底板厚度1.30 m,侧墙厚度0.90 m,中墙厚度0.80 m。下层地铁车站主体为地下两层三跨平顶直墙结构,横断面尺寸为26.20 m×15.86 m,顶板厚度1.50 m,中板厚度0.40 m,底板厚度1.20 m,侧墙厚度1.00 m,中柱的直径为0.90 m,顶板上层与隧道结构底板下层夹层土厚度为0 m。根据地质勘察报告并综合考虑计算模型需要,土层采用 Mohr-Coulomb模型,场地土层性质及力学参数见表1。在满足计算精度的要求下,车站模型尺寸选定为240.00 m×50.00 m×70.00 m。混凝土采用弹性模型模拟,密度为2 600 kg/m3,泊松比为0.2,弹性模量为4.83 GPa,模型如图2所示。

图1　位置关系

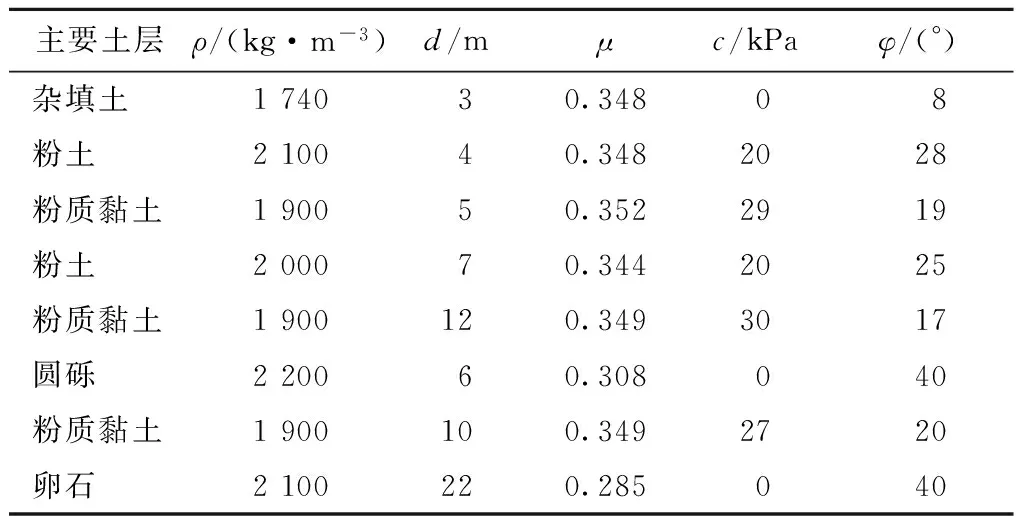
主要土层ρ/(kg·m-3)d/mμc/kPaφ/(°)杂填土174030.34808粉土210040.3482028粉质黏土190050.3522919粉土200070.3442025粉质黏土1900120.3493017圆砾220060.308040粉质黏土1900100.3492720卵石2100220.285040

图2　模型

2　动力参数选取

计算模型通过静力计算获得应力场后,再进行动力计算。

2.1边界条件

对模型进行动力响应分析计算时,由于边界对波的反射作用会对计算结果产生影响,所以计算模型边界的选取显得尤为重要。在FLAC3D中提供了两种边界条件,即静止(黏性)边界及自由场边界。静止(黏性)边界是Lysmer与Kuhlemeyer(1969年)提出的,其原理是在模型边界法向及切向上分别设置独立阻尼器,在吸收入射角大于30°的入射波时,这种方法几乎是完全有效的。然而，对于较小的入射角度或面波,仍具有一定的吸收能力,但是并不理想。

设置自由场边界，主体网格的侧边界通过自由场网格与阻尼器进行耦合,在主体网格的边界上施加自由场网格的不平衡力。自由场边界所提供的作用与无限场地是相同的,因此,面波在边界上进行传递时不会发生扭曲变形。在FLAC3D中,计算模型顶部采用自由边界,侧面则采用自由场边界,底部为基岩,为刚性边界,动荷载的输入可采用加速度时程,不需转化[10]。

2.2阻尼的选取

FLAC3D动力计算提供了瑞利阻尼、局部阻尼和滞后阻尼三种形式。计算模型选择瑞利阻尼,瑞利阻尼最初应用于结构和弹性体的动力计算中,以减弱系统的自由振动。计算时方程中的阻尼矩阵(C)的各分量与质量矩阵(M)和刚度矩阵(K)成比例,即

C=αM+βK,

(1)

式(1)中α为与质量成比例的阻尼常数,β为与刚度成比例的阻尼常数,分别具有s-1和s的量纲[11-12]。

3　加载方案与结果分析

3.1加载方案

选择国内外具有代表性的日本阪神(Kobe)地震波的加速度原始记录作为地铁车站长距离密贴下穿既有隧道结构地震反应分析的近场输入地震动,地震动加速度-时程曲线及傅里叶谱见图3。截取其含有峰值加速度的近场地震动Kobe波的前25 s时程进行计算。

地震动输入为水平方向,分为单一隧道结构(工况1)、地铁车站平行密贴下穿隧道结构(工况2)两种工况。

图3　输入地震动加速度-时程曲线及傅里叶谱

3.2结果分析

分析地铁车站长距离密贴下穿既有隧道结构的地震响应,隧道结构的监测点布置如图4所示。分析截面为隧道结构的纵向中间截面A—A处。

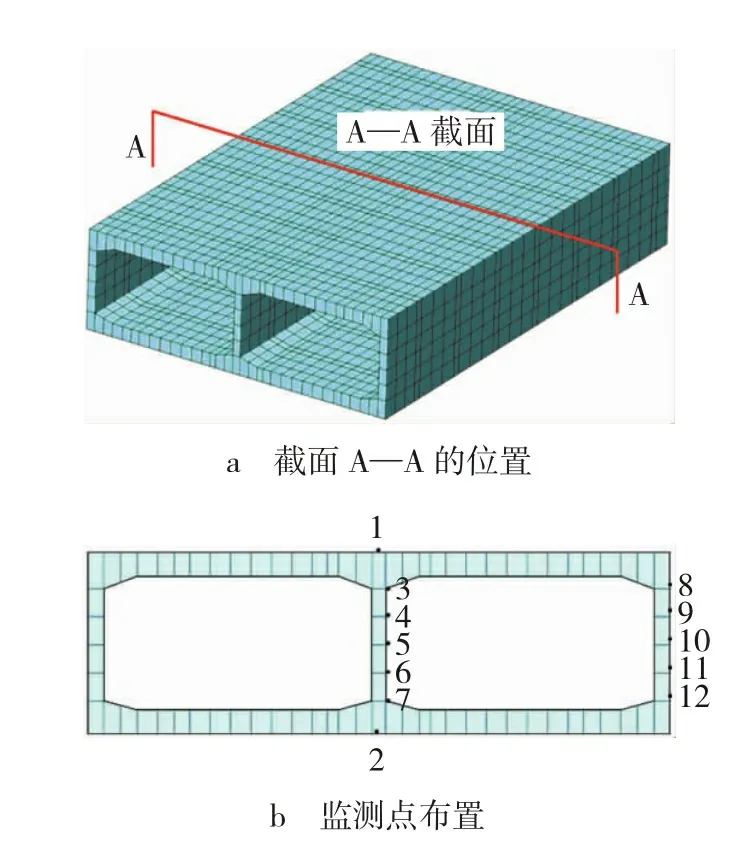
图4　监测点布置

3.2.1水平位移分析

施加水平方向的地震动后,两种工况下隧道截面A—A处顶板与底板的水平位移(s)-时程(t)曲线如图5所示。结果显示:

(1)隧道顶板与底板的位移时程曲线规律大致相同,且变化趋势相似于施加的地震波。

(2)与单一隧道结构水平位移-时程相比,长距离密贴地铁车站结构对隧道结构的相对水平位移有减弱作用,其中,工况1隧道结构顶板与底板相对水平位移最大值为2.88 cm,工况2隧道结构顶板与底板相对水平位移最大值为2.64 cm。

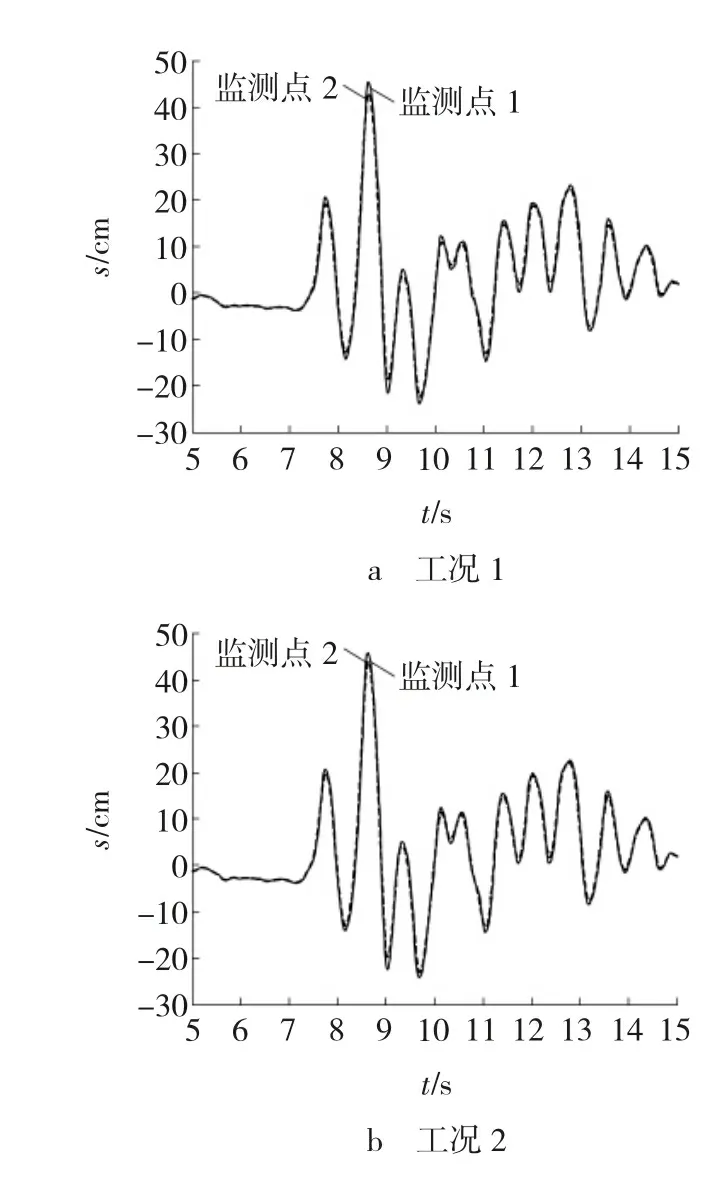
图5　隧道结构顶板与底板水平位移-时程曲线

此处定义隧道中间隔墙与侧墙不同高度处的水平位移与隧道底部水平位移的最大差值为隧道相对水平位移差(Δs)。隧道结构中间隔墙与侧墙的相对水平位移差沿高度变化值如图6所示。可作如下总结:

(1)地铁隧道的相对水平位移差在Kobe波地震动作用下呈直线形或折线形,且在水平地震波作用下隧道结构中间隔墙与侧墙的水平位移随墙体的高度增加而增加。

(2)工况1中间隔墙相对水平位移最大值为2.44 cm,侧墙相对水平位移最大值为2.19 cm;工况2中间隔墙相对水平位移最大值为2.32 cm,侧墙相对水平位移最大值为2.06 cm。单一隧道结构中间隔墙与侧墙的相对水平位移大于有密贴下穿地铁车站结构时的相对水平位移,说明密贴下穿的地铁车站结构对地震波有一定的耗能作用,减少了上部隧道结构的相对水平位移。

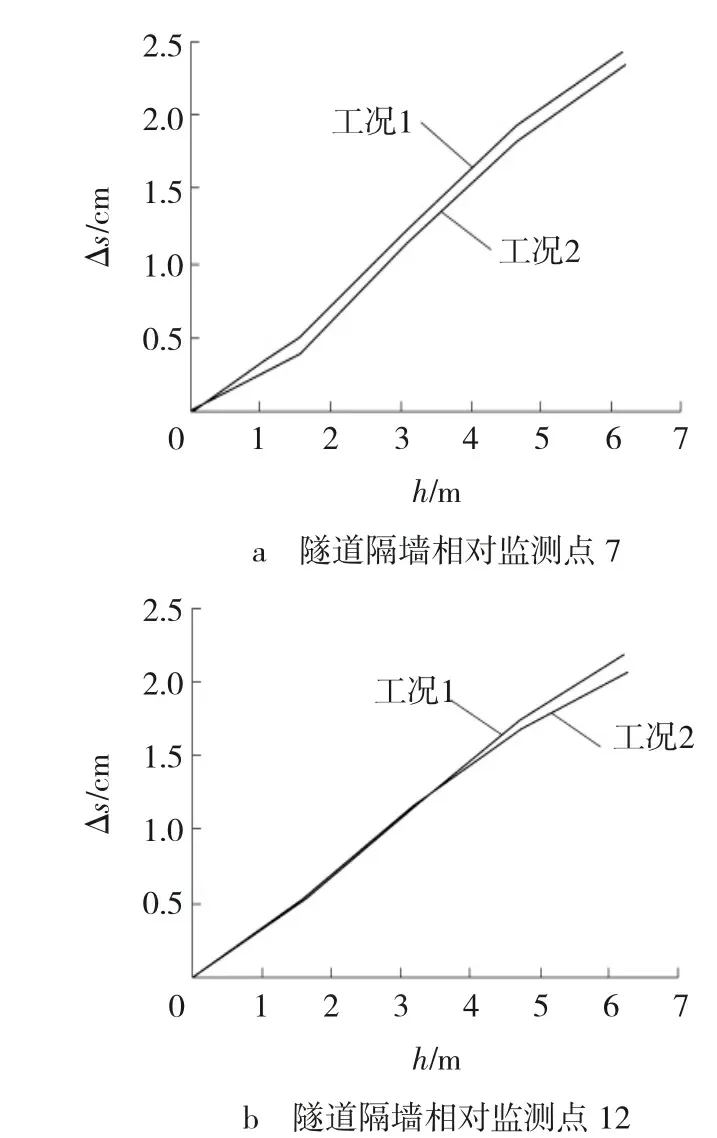
图6　隧道结构墙体相对水平位移差

3.2.2加速度分析

文中定义反应加速度峰值与输入地震波峰值之比为加速度放大系数,即加速度放大系数=反应加速度峰值/输入地震波峰值。

在输入地震动Kobe波作用下,工况2隧道顶板与底板的加速度反应时程如图7所示。两种工况下隧道各监测点的加速度放大系数见表2。通过对反应加速度的分析,可作如下总结:

(1)隧道顶板与底板的加速度反应时程曲线与基岩输入地震波的形态基本相近,隧道结构顶板的水平加速度(a1)峰值大于底板的水平加速度峰值。

(2)与单一隧道结构的加速度-时程曲线相比,密贴地铁车站结构对隧道结构的动力响应有减弱效果。密贴下穿地铁车站结构存在时,对上方隧道结构底板加速度响应的减弱效应最为明显,最大减弱比率为17.44%。隧道结构中间隔墙与侧墙底部的加速度响应的减弱效应也较为明显,最大减弱比率分别为15.43%和14.20%,且靠近隧道结构底部的减少幅度较大。这表明,密贴下穿地铁车站对上部隧道结构的动力加速度响应有不同程度的减弱效应,且越靠近车站结构减弱幅度越大,下部车站结构的减震耗能现象存在于某一局部范围内。

图7　工况2隧道顶板与底板加速度-时程曲线

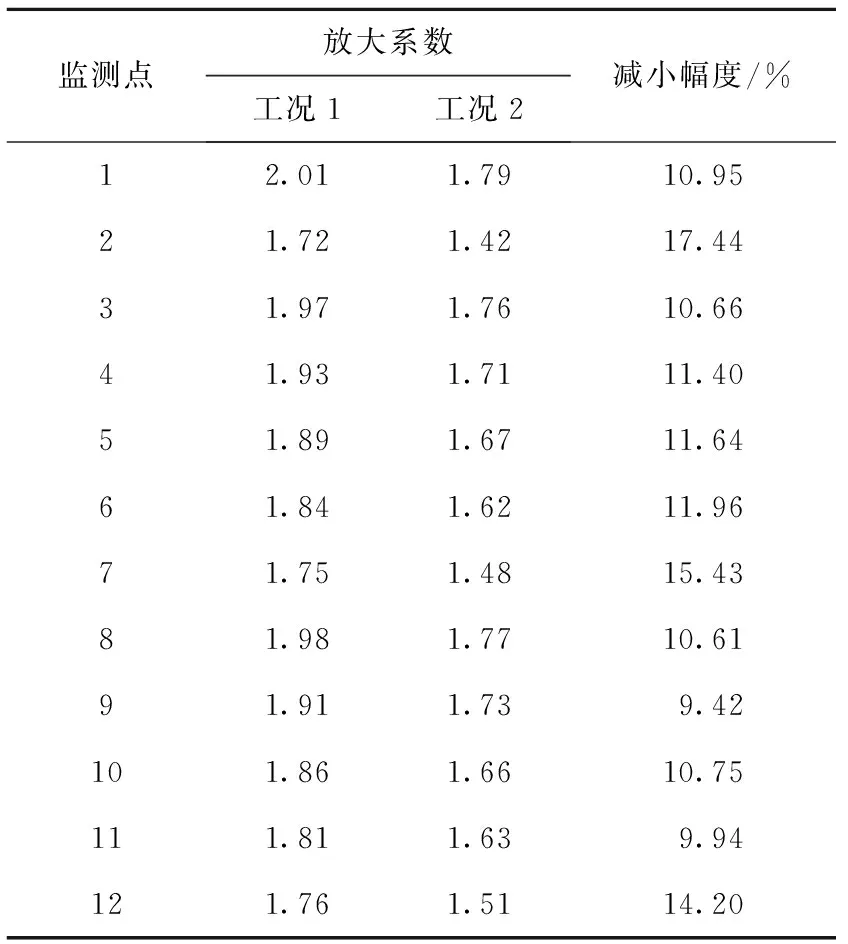
监测点放大系数工况1工况2减小幅度/%12.011.7910.9521.721.4217.4431.971.7610.6641.931.7111.4051.891.6711.6461.841.6211.9671.751.4815.4381.981.7710.6191.911.739.42101.861.6610.75111.811.639.94121.761.5114.20

4　结　论

(1)输入水平方向的地震波,有无地铁车站结构的隧道结构的位移-时程与加速度-时程曲线规律相同,均随深度的增加而减小,且变化趋势相似于施加的地震波。

(2)隧道顶板与底板的加速度-时程曲线与基岩输入地震波的形态基本相近,隧道结构顶板的水

平加速度峰值大于底板的水平加速度峰值。

(3)与单一隧道结构的位移-时程和加速度-时程相比,密贴地铁车站结构对隧道结构的动力响应有减弱效果。下穿地铁车站对上部隧道结构的动力加速度响应有不同程度的减弱效应,且越靠近车站结构减弱幅度越大,下部车站结构的减震耗能现象存在于某一局部范围内。

[1]张波, 陶连金, 姜峰, 等. 地铁超近距交叉结构在水平地震荷载下的响应影响分析[J]. 铁道建筑, 2011(11): 47-50.[2]陶连金, 王文沛， 张波, 等. 竖向强震作用下密贴地铁地下交叉结动力响应分析[J]. 岩土工程学报, 2012(3): 433-437.

[3]CHEN G X, ZHUANG H Y. Analysis on the earthquake response of subway station based on the substructure subtraction method[C]//Proceedings of the Third International Conference on Earthquake Engineering. Nanjing: [s.n.], 2004: 195-199.

[4]庄海洋, 陈国兴, 胡晓明. 两层双柱岛式地铁车站结构水平向非线性地震反应分析[J]. 岩石力学与工程学报, 2006(S1): 3074-3079.

[5]LEE V W, TRIFUNAC M D. Response of tunnel stoincident SH waves[J]. Journal of the Engineering Mechanics Division, 1979, 105(4): 643-659.

[6]BALENDRA T, THAMBIRATNAM D P, KOH C G, et al. Dynamic response of twin circular tunnels due to incident SH waves[J]. Earthquake Engineering and Structural Dynamics, 1983, 12(2): 181-201.

[7]梁建文, 张浩, VINCENT W. 平面P波入射下地下洞室群动应力集中问题解析解[J]. 岩土工程学报, 2004(6): 815-819.

[8]陈磊, 陈国兴, 龙慧. 地铁交叉隧道近场强地震反应特性的三维精细化非线性有限元分析[J]. 岩土力学, 2010(12): 3971-3976, 3983.

[9]陈磊, 陈国兴. 近断层强地震动下双层竖向重叠地铁隧道的地震反应[J]. 防灾减灾工程学报, 2008(4): 399-408.

[10]刘波, 韩彦辉. FLAC原理、实例与应用指南[M]. 北京: 人民交通出版社, 2005.

[11]赵伯明, 蒋英礼, 陈靖. 软土地铁车站结构在三维强地震动作用下的响应分析[J]. 中国铁道科学, 2009(3): 45-50.

[12]熊良宵, 李天斌, 刘勇. 隧道地震响应数值模拟研究[J]. 地质力学学报, 2007(3): 255-260.

(编辑徐岩)

Analysis on seismic response of long-distance and closely-attached subway station to existing tunnel structure

TAOLianjin,YANDongmei,LIJidong,GUOFei,ZHOUMingke

(Institute of Geotechnical & Underground Engineering, Beijing University of Technology, Beijing 100124, China)

This paper introduces a model of tunnel structures designed specifically to investigate the seismic response characteristics of the long-distance and closely-attached underground space. This model follows from a targeted analysis of what occurs with a newly-built subway station structure and the upper tight stick of an existing tunnel structure using finite difference software FLAC3D. The paper goes further by analyzing the seismic response of the tunnel with or without a subway station passing through a tunnel, as is conditioned by inputting Kobe earthquake waves. The calculation shows that inputting the horizontal direction earthquake waves yields roughly the same law underlying curves of relationship between displacement time history and acceleration time history related to a tunnel structure with or without Metro stations, as is illustrated by the curves which tend to decrease with an increasing depth and show a changing trend similar to the earthquake waves applied; the roof slab and bottom slab of a tunnel have a horizontal acceleration with time-history curves basically similar to the seismic wave of the bedrock, and the roof slab of a tunnel structure produces a horizontal acceleration with a peak greater than that of the bottom slab; compared with the curve between the displacement time history and acceleration time history of a single tunnel structure, a closely-attached subway station structure exerts a weakening effect on the dynamic response of the tunnel structures; and a subway station passing through the tunnel has a weakening effect of varying degrees on dynamic acceleration response of the upper structure tunnel and yields an increasingly greater reduction, the closer it is to a station structure, suggesting the occurrence of damping energy dissipation, as in the case of lower part of the station structure.

existing tunnel structure; seismic response; subway station; closely-attached; finite difference procedure FLAC3D

2014-04-01

国家自然科学基金重点项目(51038009)；北京市自然科学基金重点项目(8111001)

陶连金(1964-),男，黑龙江省鸡西人，教授，博士，博士生导师，研究方向：岩土工程与地下工程，E-mail：ljtao@bjut.edu.cn。

10.3969/j.issn.2095-7262.2014.03.017

U452.28

2095-7262(2014)03-0301-05

A