粒子群改进算法在配电网故障定位中的应用

赵金宪,　涂　展,　谢　阳

(黑龙江科技大学 电子与信息工程学院, 哈尔滨 150022)



粒子群改进算法在配电网故障定位中的应用

赵金宪,涂展,谢阳

(黑龙江科技大学 电子与信息工程学院, 哈尔滨 150022)

为了满足含分布式电源配电网故障定位的要求,对传统二进制粒子群算法进行改进,利用改进二进制粒子群算法(BPSO)解决配电网故障定位问题。改进BPSO初始化随机数采用均匀分布,同时引入收缩因子和线性变换的惯性权重来提升算法收敛于最优解的能力,避免陷入局部最优,提升故障定位的精确性。对算例配电网中的多种故障情形进行仿真分析,包含少量故障信息畸变的情况,诊断结论全部正确。仿真结果表明,改进算法在精确性和收敛速度上均优于传统粒子群算法,对含分布式电源的配电网故障定位具有一定的有效性和容错性。改进BPSO可以满足电网定位对准确和实时性的要求。

配电网; 故障定位; 传统二进制粒子群; 改进二进制粒子群; 容错性

0　引　言

随着大量分布式电源接入配电网,对其故障定位提出了更高的要求。目前,配电网故障定位方法可分为矩阵法[1-2]和智能优化算法[3-8]两类,这两种故障定位方法所用到的故障信息,均为网络中每个开关节点处的FTU采集到的过电流信息。矩阵法需要FTU上传的信息具有较高的精确性,因此,该方法容错性较差。基于优化算法的故障定位方法属于人工智能方法的一种,可以得到较为精确的诊断结果,诊断速度快,容错性好。常用的优化算法包括遗传算法[3]和群智能算法[4-8],其中群智能算法中的粒子群算法应用最为广泛。遗传算法具有全局搜索能力,但它的交叉和变异环节,使计算量增大,求解过程复杂;粒子群算法较遗传算法更简捷,收敛速度更快,稳定性好,但容易陷入局部最优解,影响解的准确性。

分布式电源的接入能够引起配电网的结构和潮流变化,使故障定位的情形变得更为复杂,更需要故障定位算法具有很高的准确性。笔者为了提升粒子群算法准确收敛于最优解的能力,在传统粒子群算法的基础上,对算法进行改进。希望改进算法能够提升粒子群算法全局搜索的能力,使收敛速度更快,不易陷入局部最优解,并将改进粒子群算法应用于解决含分布式电源配电网的故障定位问题。

1　二进制粒子群算法与改进方法

1.1二进制粒子群算法基本原理

粒子群算法(Particle Swarm Optimization, PSO)是Kennedy和 Eberhart 在群智能算法的基础上,提出的一种智能随机优化算法。PSO通过模拟鸟类捕食行为,取每个个体作为粒子,在高维空间构造“粒子群”,粒子群在解空间按照既定规则运动,所处位置不断变化。通过评价适应度函数的值,从而确定粒子最优位置[9]。

在PSO算法中,每个粒子在解空间所处的位置即为优化问题的解,同时每个粒子还具有速度值的概念,决定粒子飞行的方向和距离。整个种群通过追随最优位置上的粒子完成最优解搜索。其中,每个粒子经过的最好位置称为个体极值pbest。 全部粒子经过的最好位置称为全局极值gbest。

设目标搜索空间为N维,第i个粒子在空间的位置和速度值分别为xi=(xi1,xi2,…,xiN)和vi=(vi1,vi2,…,vin)。将粒子i的位置代入到目标函数,根据得到的适应值,评价粒子位置的优劣,同时得到个体极值pbest和全局极值gbest。根据式(1)和(2)更新粒子的速度和位置。

(1)

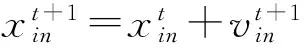
(2)

在实际应用中,许多优化问题是以离散或二进制变量为目标的。上述普通PSO只能处理连续函数的优化问题,因此,文献[10]提出了一种二进制粒子群优化算法(BinaryParticleSwarmOptimization,BPSO)。BPSO中粒子的位置是从概率角度定义的,令每一维粒子的位置xin只取0 或1,而速度vin为xin取1的概率,若速度vin取值较大,xin为1的概率就较大,反之,xin为0的概率变大。因此,对于BPSO,粒子位置的更新公式为:

(3)

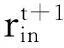
(4)

1.2二进制粒子群算法的改进

BPSO 具有优化过程简捷,收敛速度快,稳定性高等优点。但是该算法容易陷入局部最优解,计算精度不高。为解决这一问题,将BPSO进行改进,使其更加适用于对配电网故障定位的精确度要求。改进措施为以下三个方面。

(1)随机数选取。BPSO 对种群粒子初始化采用随机方法,文献[11]指出，由符合均匀分布的粒子构成的种群,比随机初始化的种群更能从统计学角度反映适应度函数的特性。因此,为提升全局搜索能力,采用均匀分布初始化粒子群的位置和速度。

(2)速度更新公式的改进。学习因子c1、c2能够反映粒子群之间的信息交流,因为c1较大将使过多粒子在局部徘徊,c2较大则极易使粒子陷入局部最优,所以引入Clerc提出的收缩因子,将式(1)变为

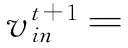
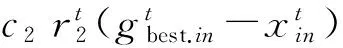
(5)

其中，

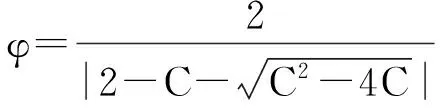
C=c1+c2。

为保证算法顺利求解,C须大于4。

(3)惯性权重值的动态选取。较大的ω有利于提升算法的全局搜索能力,较小的ω则会增强算法的局部搜索能力。为选取较好的权重,采用线性变化的方法,使ω从最大值ωmax线性减小到最小值ωmin,因此ω更新公式为

(6)

其中,ωmax、ωmin分别表示ω的最大与最小值,t为当前迭代次数,tmax为最大迭代次数。

2　故障定位模型和算法流程

2.1改进BPSO故障定位原理

配电网故障时,网络中各个开关节点处的FTU 能够检测到故障过电流信息,从而形成故障数据上传至调度中心,调度中心的故障定位系统通过分析故障数据信息,来判定故障区段,实现故障的定位。由于配电网故障信息是离散的,所以文中采用BPSO实现配电网的故障定位。BPSO中粒子维数表示网络中目标区段总数;粒子的位置,即目标函数最优解,代表电网中各个区段状态值。其中每个区段的取值只为0或1,分别表示正常或故障状态。通过式(7)对粒子位置评价优劣,更新个体极值pbest和全局极值gbest,同时更新种群粒子的速度和位置。当运算满足停止条件时,所输出的全局最优位置即为目标函数最优解,对应配电网各个区段的状态值。2.2适应度函数的构造

适应度函数的构造是准确定位故障区段的关键,文献[4]的故障定位模型,其构建方式对于含分布式电源配电网的故障定位具有较好效果：

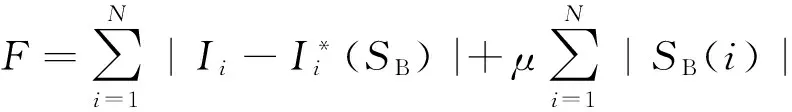
(7)

含分布式电流的配电网与辐射状配电网故障定位的不同点是,分段开关FTU除检测故障过电流发生外,还要判断过电流方向。图1为双电源配电网。

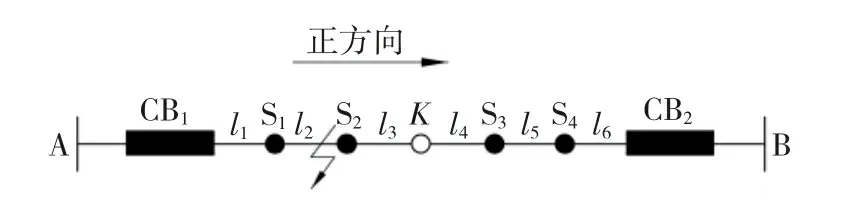
图1　简单双电源配电网

图1中,A、B为电源端，CB1、CB2为进线断路器，l1、l2、l3、l4、l5、l6为配电网中的设备编号，S1、S2、S3、S4为分段开关，K为联络开关,K=0或1分别表示常开或常闭,正常运行时,K为常开。每个开关均设有FTU来检测故障电流。现在规定电源A为参考电源,其电流方向为正方向,联络开关闭合,于是如图1中l2段发生故障时,CB1和S1流过正向故障电流,状态为1;CB2、S2、S3、S4流过反向故障电流,状态为-1。

对于S1来说,当l2、l3、l4、l5、l6故障时,S1有正方向电流流过,当l1故障时,S1有反方向电流流过,因此(∨为逻辑“或”,&为逻辑“与”)

S1正方向状态为:l2∨l3∨(K&(l4∨l5∨l6)),

反方向状态为:l1&K;

S1的开关函数可表示为:

I*(S1)=l2∨l3∨(K&(l4∨l5∨l6))-l1&K。

同理,可得到I*(CB1)、I*(S2)、I*(S3)、I*(S4)、I*(CB2)。将上述开关函数代入到式(3),可得到最终配电网故障定位的适应度函数。显然,将各开关FTU所采集到的故障信息代入式(7)中,使式(7)取得最小值的解,就是最能表征配电网故障区段情况的,由此将故障定位问题即转变为求解目标函数最小值的问题。

2.3算法流程

改进的算法流程可以总结为以下六点。

(1)初始化粒子群参数。初始化种群规模M, 最大迭代次数maxC,学习因子c1、c2,设定权重最大值和最小值ωmax、ωmin,个体极值pbest,全局极值gbest,令迭代次数t=0。

(2)根据配电网开关节点信息,确定粒子维数,通过计算各节点期望函数来构建配电网故障定位的适应度函数。

(3)评价每个粒子的适应度。按均匀分布(Uniform distribution)初始化种群粒子位置xi=(xi1,xi2,…,xin),令粒子速度vi=(vi1,vi2,…,vin)为0。记录当前各个粒子的位置,并将适应度值存储在pbest中,同时记录全部pbest中适应值最优个体的位置,将它的适应值存储于gbest。

(4)利用式(3)～(5)更新粒子的位置和速度,利用式(6)更新权重。

(5)更新pbest和gbest。 将每个粒子适应度值与其经历过的最好位置比较,如果优于之前的最好位置,则将其作为当前最优位置;同时比较所有pbest和gbest,更新gbest。

(6)若达到最大迭代次数,则停止计算。否则,返回步骤(4),重新迭代计算。粒子群全局最优位置即为配电网各区段状态。

3　算例分析

文中算例配电网见图2。以图2为例进行仿真分析。

图2　算例配电网

对于含分布式电源的配电网络,进行故障定位时需要考虑故障过电流方向性,此种情形下的网络节点按位置不同,分为处于故障区段与参考电源之间的节点和处于参考电源支路上,首个故障区段与参考电源以下的节点。其中,第一类节点的状态全为1;第二类节点的状态有三种情况:非参考电源在该节点流过反向电流,状态为-1;未流过反向电流,状态为0;流过正向故障电流,状态为1。

图2中,V为系统电源,DG1、DG2为分布式电源，K1、K2为联络开关,用来控制分布式电源的接入，CB1、CB2、CB3为进线断路器;其余黑色圆点表示分段开关(编号S1～S17)，圆点之间的线段为馈线区段(编号l1～l20)，令V为参考电源端,因此网络中电流正方向如图中箭头所示。利用文中提出的改进BPSO,对图2配电网中的多种故障情形进行故障定位,参数设置为:粒子维数设为20,种群规模为80,收缩因子φ为4.1,学习因子c1=c2=2.05,惯性权重最大值wmax=0.9,最小值wmin=0.4,最大迭代次数设为100,输入的20维故障信息为定义为[CB1,CB2,CB3,S1,S2,…,S17]。

文中设定的故障情形以K1、K2状态作为分类依据,[K1,K2]为分布式电源开关系数,K1=0或1分别表示分布式电源DG1未接入或接入配电网;K2=0或1表示DG2未接入或接入配电网。故障情形选择单点故障和2点故障,同时在伴有少量信息畸变条件下进行仿真,程序连续运行50次,仿真结果如表1所示。

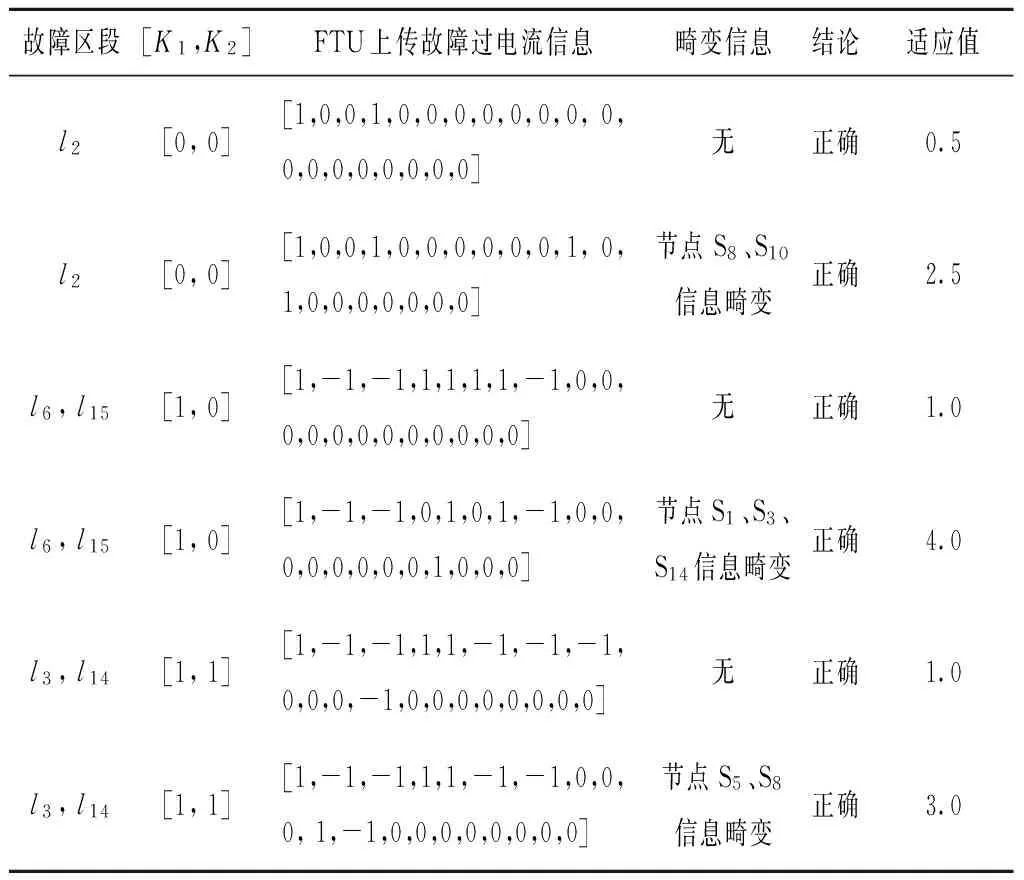
表1　多种故障情况测试结果

选取l6和l15区段故障时,并伴有S1、S3、S14点信息畸变情况,连续运行50次。发现普通BPSO会有一定概率陷入局部最优,而采用改进BPSO得到的诊断结论全部正确。正确率比较见表2。

表2　两种算法正确率比较

改进BPSO与普通BPSO的收敛趋势比较如图3所示。显然改进BPSO的收敛速度要稍快于普通BPSO。综上,改进BPSO相比较于普通BPSO,更能满足配电网故障定位对准确性和实时性的要求。

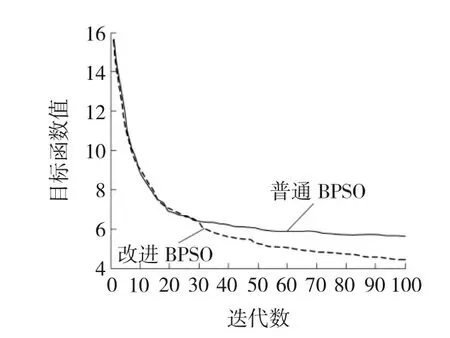
图3　两种算法收敛趋势

4　结束语

改进BPSO算法优于传统粒子群算法。文中采用改进的BPOS对含分布式电源的配电网进行故障定位,可以提升对最优解的全局搜索能力,有效防止了普通BPSO应用中存在的“早熟早敛”现象。算例仿真多种故障情形,包括单点和两点故障并伴随有少量信息畸变的情况,故障定位结论全部正确。改

进BPSO收敛速度快,稳定性好,能够满足电网故障定位对准确性和实时性的要求。

[1]蒋秀洁, 熊信银, 吴耀武, 等. 改进矩阵算法及其在配电网故障定位中的应用[J]. 电网技术, 2004, 18(9): 60-63.

[2]罗梅, 杨洪耕. 配电网故障定位的一种改进通用矩阵算法[J]. 电力系统保护与控制, 2012, 40(5): 34-37.

[3]严太山, 崔杜武, 陶永芹. 基于改进遗传算法的配电网故障定位[J]. 高电压技术, 2009, 35(2): 255-259.

[4]张颖, 周韧, 钟凯. 改进蚁群算法在复杂配电网故障区段定位中的应用[J]. 电网技术, 2011, 35(1): 224-228.

[5]卢志刚, 董玉香. 基于改进二进制粒子群算法的配电网故障恢复[J]. 电力系统自动化, 20, 24(6): 39-43.

[6]周湶, 郑柏林, 廖瑞金, 等. 基于粒子群和差分进化算法的含分布式电源配电网故障区段定位[J]. 电力系统保护与控制, 2013, 41(4): 33-37.

[7]卢志刚, 杨国良, 张晓辉, 等. 改进二进制粒子群优化算法在配电网络重构中的应用[J]. 电力系统保护与控制, 2009, 37(7): 30-34.

[8]李超文, 何正友, 张海平, 等. 基于二进制粒子群算法的辐射状配电网故障定位[J]. 电力系统保护与控制, 2009, 37(7): 35-39.

[9]KENNEDY J, EBERHART R C. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE Press, 1995: 1942-1948.

[10]MAURICE C, KENNEDY J. The particle swarm explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.

[11]高飞, 童恒庆. 基于改进粒子群优化算法的混沌系统参数估计方法[J]. 物理学报, 2006, 55(2): 577-582.

(编辑徐岩)

Application of improved binary particle swarm optimization for fault location in distribution network with distributed generation

ZHAOJinxian,TUZhan,XIEYang

(School of Electronics & Information Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is focused specifically on seeking a solution to the fault location in distribution network by improving the traditional binary particle swarm optimization(BPSO) algorithm, as a part of our efforts to fulfill the requirement of fault location in distribution network with distributed generations. The improved BPSO algorithm operates by initializing random number using uniform distribution, introducing the constriction factor and the inertia weight of linear transformation for improving algorithm’s ability to keep convergence on the optimal solution, and thereby improving the accuracy of fault location, thanks to the prevention of local optimum. The improved BPSO is validated by the ultimate diagnosis due to a simulation analysis of a variety of faults, including fault information distortion, occurring in distribution network. The simulation shows that the improved algorithm is superior to the conventional BPSO in terms of accuracy and convergence speed and thus demonstrates a greater effectiveness and fault tolerance for the distribution network fault location with distributed generations.

distribution network; fault location; traditional binary particle swarm optimization; improved binary particle swarm optimization; fault tolerance

2013-07-18

赵金宪(1970-)，男，吉林省舒兰人，教授，博士，研究方向：智能控制技术，E-mail:zjx5579@163.com。

10.3969/j.issn.2095-7262.2014.03.012

TM711

2095-7262(2014)03-0277-05

A