MINITAB在制药企业产品质量回顾中的应用

北京北大维信生物科技有限公司（100094）孟春玲 王晓峰

北京市海淀区食品药品监督管理局（100097）孔莉△

企业来说是熟练的，但对大部分国内药品生产企业，尤其是口服制剂企业的质量管理人员来说却相当陌生，要想正确实施无疑是困难重重。因此，采用何种科学、有效的统计工具就显得至关重要。因此，我厂请北京市海淀区食品药品监督管理局领导对我厂的数据统计分析工作进行了指导，尝试在年度回顾中引进统计工具软件Minitab进行统计分析，收到了较好的效果。

通过对我公司某产品2012年度质量回顾中数据统计分析，使用了Minitab（版本号：16）中控制图、柱状图、帕累托图、能力分析的四种功能。具体用途如下：关键中间控制点控制、成品的检验结果趋势分析、原辅料质量状况评价、偏差的发现与预防。本文就我公司在上述Minitab应用过程中的方法、标准进行了研究，并结合应用实例进行了阐述。

1 Minitab控制图功能在关键中间控制点控制数据统计中的应用

1.1 概述 控制图是质量管理的一种重要手段和工具，是对过程质量特性进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图。控制图是给定的数据值/数组均值与数据号/数组号在平面直角坐标系中对应的一种图形；图上有中心线（CL，Central Line）、上控制线（UCL，Upper Control Line）和下控制限（LCL，Lower Control Line），并有按时间顺序抽取的样本统计量数值的描点序列。UCL、CL、LCL统称为控制线（Control Line）。中心线是所控制的统计量的平均值，上下控制界限与中心线相距数倍标准差/极差。计算控制限是为了显示仅存在变差的普通原因时子组的均值和极差的变化和范围[1]。

我公司在关键中间控制点控制数据统计中使用Minitab控制图功能。

1.2 方法分类 由于我公司年度质量回顾数据均为计量数据，所以应用计量型控制图，包括IX-MR（单值移动极差图）、Xbar-R（均值极差图）、Xbar-S（均值标准差图）。IX-MR（单值移动极差图）描绘单个观测值的数据，用于观测值不好获得或观测数据较少的情况；Xbar-R（均值极差图）适用于2≤子组大小≤8的数据，用于工序持续时间较长、观测值较多的情况；Xbar-S（均值标准差图）适用于子组大小≥8的数据，用于工序持续时间极长、观测值极多的情况。

我公司由于没有极大数据量，故不使用Xbar-S（均值标准差图）功能。

1.3 公式和系数 计算平均极差（R）及过程均值（X）：①R＝（R1+R2+…+Rk）/k（k表示子组数量）；②X＝（X1+X2+…+Xk）/k。计算控制限：③UCLx＝X+ A2R；④LCLx＝X-A2R；⑤UCLR＝D4R；⑥LCLR＝D3R。[注：式中A2，D3，D4为常系数，决定于子组样本容量。单值移动极差图（IX-MR）子组样本容量n＝1；均值极差图（Xbar-R）子组样本容量n＝2～8。其系数值见国家标准《常规控制图》（标准编号：GB/T 4091-2001）中“计量控制图计算控制线的系数表”。我公司采用Minitab控制图功能时由该软件根据子组样本容量按上述标准自动计算生成。]

1.4 图形生成 在Minitab中选择“统计-控制图-子组的变量控制图”或者“统计-控制图-单值的变量控制图”。

1.5 变差的模式检验 根据国家标准《常规控制图》（标准编号：GB/T 4091-2001）将UCL和LCL之间等分为六个区，标号为A、B、C、C、B、A，两个A区、B区、C区关于中心线对称。模式检验适用于Xbar图和单值（X）图。共有八个模式检验：①1个点落在A区以外；②连续9点落在中心线同一侧；③连续6点递增或递减；④连续14点中相邻点交替上下；⑤连续3点中有2点落在中心线同一侧的B区以外；⑥连续5点中有4点落在中心线同一侧的C区以外；⑦连续15点落在中心线两侧的C区内；⑧连续8点落在中心线两侧且无一在C区内。

我公司采用Minitab控制图功能时在该软件“Xbar-R选项”中设置以上八个检验模式，任何检验异常都应结合实际生产进行分析，如变差属于生产偏差，应按偏差处理并制定纠正预防措施。而另一个普遍采用的统计学工具软件SPSS中设置的模式检验项目和项目的评估数据点数量与国家标准有所不同，这也是我公司采用Minitab软件的重要原因。

1.6 应用实例 以下是我公司某产品胶囊充填工序装量差异检查数据统计实例，内控标准上限：0.391g，内控标准下限：0.361g；子组样本容量：5。使用Xbar-R（均值极差图），计算和设置按照上述3、4、5项进行。统计数据见附表1，Xbar-R控制图信息见附表2；Xbar-R控制图见附图1。

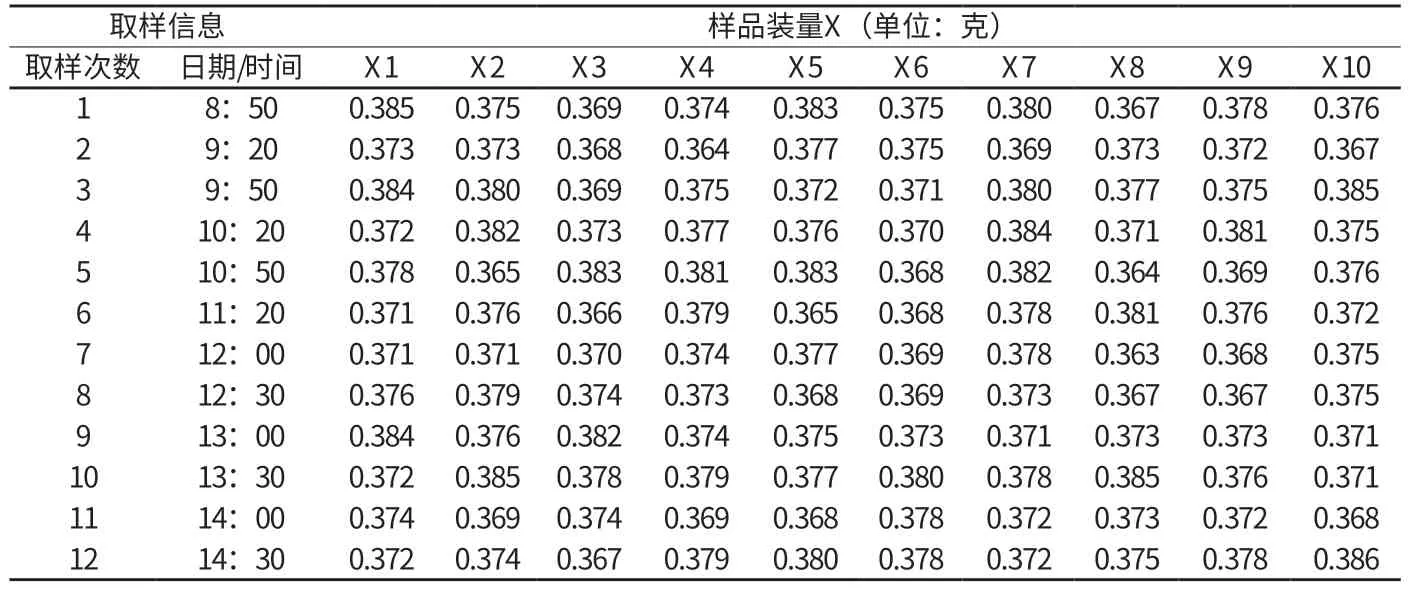
附表1 某产品胶囊充填工序装量差异检查数据

附表2 某产品胶囊充填工序装量差异检查数据的Xbar-R控制图信息

附图1 某产品胶囊充填工序装量差异检查数据的Xbar-R控制图

附图1显示，均值图各点都在控制上下限范围内；均值图没有数据超过内控标准限；极差图各点都在控制上下限范围内。按照“1.5变差的模式检验”中8个检验标准进行检验未见异常。说明生产过程无异常，充填过程药囊装量平稳可控。

2 Minitab柱状图功能在原辅料质量状况评价中的应用

2.1 概述 柱状图主要用于数学统计学科中，是一种以长方形的长度为变量的表达图形的统计报告图，由一系列高度不等的纵向条纹表示数据高低的情况，用来比较两个或以上的值，易于比较各组数据之间的差别[2]。

我公司在原辅料质量状况评价数据统计中使用Minitab直方图功能，直方图属于柱状图的一种，但较一般的柱状图而言，直方图可以表达两个不同的变量。

2.2 方法 直方图将样本值划分为许多称为区间的数据区间，使用条形表示落于每个区间内的观测值的数量（频率）。条形高低代表频率的多少，而多个条形的汇总显示了在相邻的多个数据区间上观测数据出现频次的分布情况。

2.3 图形生成 在Minitab中选择“图形-直方图”。

2.4 变差的模式检验 正常型直方图是指数据基于正态分布处于稳定的图型，它的形状是中间高、两边低，左右近似对称。近似是指直方图多少有点参差不齐，主要看整体形状。见附图2。

附图2 正常型直方图

异常型直方图种类则比较多，所以如果是异常型，还要进一步判断它属于哪类异常型，以便分析原因、加以处理。下面是几种比较常见的情况。

2.4.1 孤岛型 在直方图旁边有孤立的小岛出现，当这种情况出现时过程中有异常原因。如原料发生变化、不熟练的新工人替人加班、测量有误等，此时应急时查明原因、采取措施。见附图3。

附图3 孤岛型直方图

2.4.2 双峰型 直方图中出现两个峰是由于观测值来自两个总体、两个分布的数据混合在一起造成的。如两种有一定差别的原料所生产的产品混合在一起，或者就是两种产品混在一起，此时应当加以分层。见附图4 。

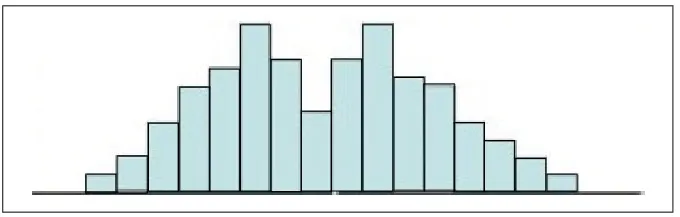
附图4 双峰型直方图

2.4.3 折齿型 直方图出现凹凸不平的形状是因作图时数据分组太多、测量仪器误差过大或观测数据不准确等造成的，此时应重新收集数据和整理数据。见附图5。

附图5 锯齿型直方图

2.4.4 陡壁型 直方图像高山的陡壁向一边倾斜通常表现在产品质量较差时，为了符合标准的产品，需要进行全数检查，以剔除不合格品。当用剔除了不合格品的产品数据作频数直方图时容易产生这种陡壁型，这是一种非自然形态。见附图6。

附图6 陡壁型直方图

2.4.5 偏峰型 偏峰型直方图是指图的顶峰有时偏向左侧、有时偏向右侧，见附图7。由于某种原因使下限受到限制时，容易发生偏左型。如用标准值控制下限，摆差等形位公差，不纯成分接近于0，疵点数接近于0或由于工作习惯都会造成偏左型。由于某种原因使上限受到限制时，容易发生偏右型。如用标准尺控制上限，精度接近100%，合格率也接近100%或由于工作习惯都会造成偏右型。

附图7 偏峰型直方图

2.4.6 平顶型 当直方图没有突出的顶峰，呈平顶型，见附图8。形成这种情况一般有三种原因：①与双峰型类似，由于多个总体、多总分分布混在一起。②由于生产过程中某种缓慢的倾向在起作用，如工具的磨损、操作者的疲劳等。③质量指标在某个区间中均匀变化。

附图8 平顶型直方图

2.4.7 拟合正态曲线并使用Minitab计算超标累计概率 在Minitab中选择“图形-直方图-包含拟合”，将直方图数据按正态分布拟合一条曲线，由此可以按照正态方程进行积分求各数据点的频次概率或者数据范围的频次累计概率（如超过标准上限、下限的频次累计概率），我企业认为：如超标概率不大于5%（一般采用的显著性水平），超标概率是可接受的。在Minitab中选择“计算-概率分布-正态”，可自动计算概率或累计概率。

2.5 应用实例 以下是我公司某厂供货的某原料水分检测数据统计实例，内控标准上限：14.5%；内控标准下限：0。使用直方图，数据、标准均除去百分号，将0～14.5的数据范围划分为长度为0.2的数据区间，使用条形表示落于每个区间内的观测值的数量（频率）。统计数据见附表3，数据直方图见附图9。

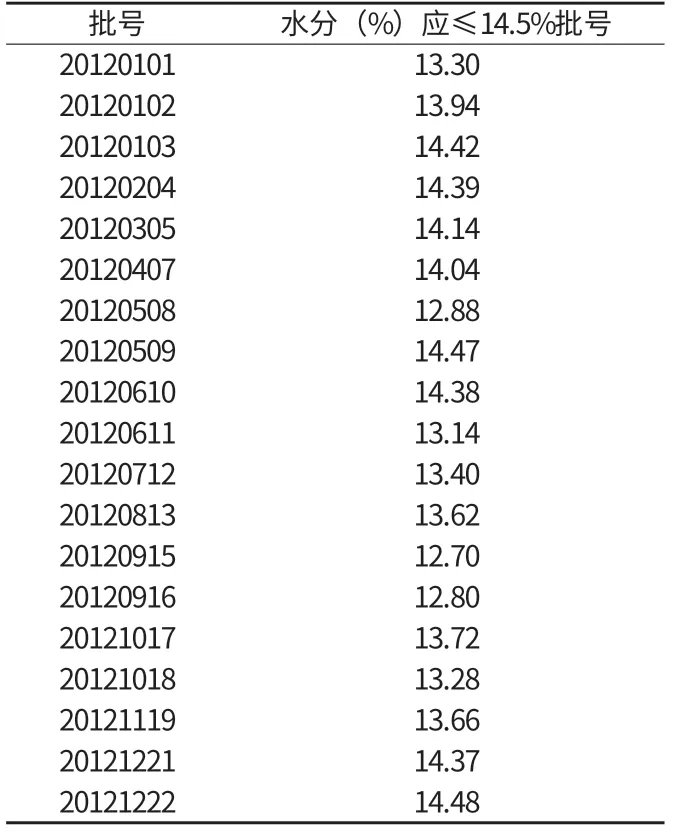
附表3 某厂供货的原料水分检测数据

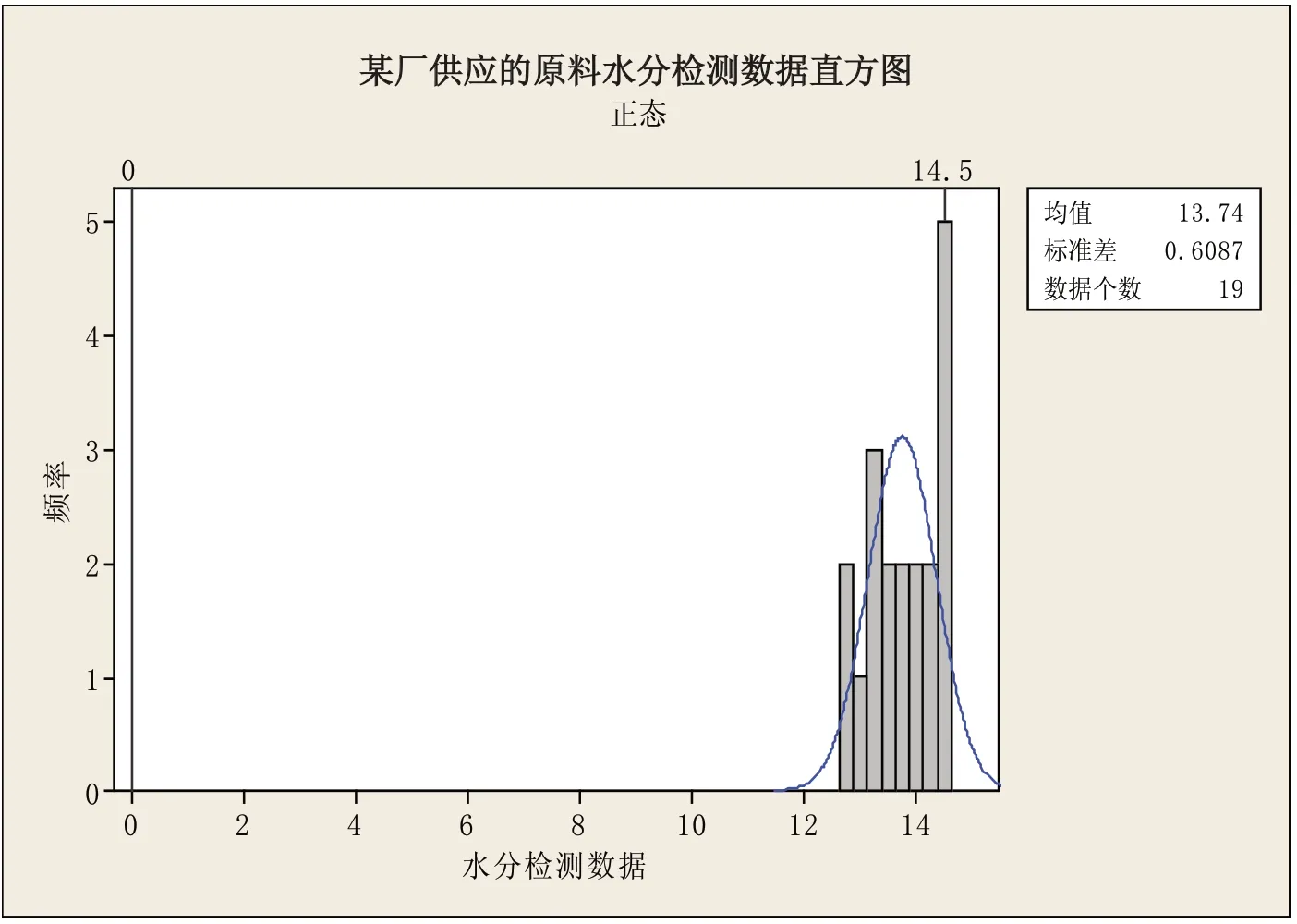
附图9 某厂供应的原料水分数据直方图

通过上述数据可以得出以下结论：水分整体比较偏高，大多在13.0%以上，呈偏峰型。有10.71%超出水分标准（14.5%）的累计概率，超标累计概率＞5%；建议供货商降低该原料水分含量指标。

3 Minitab帕累托图功能在偏差的发现与预防中的应用

3.1 概述 1897年古希腊哲学家发明、后由意大利经济学家Pareto氏为了分析国民的贫富分布状况作国民财富统计时发明的，故用其名叫“帕累托”图。帕累托图又称不良分析图，主要用途在对于工厂发生的不良情况采取对策。产品的变异或不良品的原因很多，但实际影响较大者只有其中的2～3项，也就是说这2～3项原因而主要地影响了产品。在工厂管理中如能就影响品质最大的原因加以改善，必能收到很大的效果[1]。

我公司在偏差的发现与预防数据统计中使用Minitab帕累托图功能。

3.2 方法 ①依不良原因、类别分别算出不良数目，整理成可用资料，同项目数量集计。②以不良数大小按项目自左至右排列，将集计资料的频率或件数的多少顺位排列。③横坐标为不良项目，纵坐标为不良频率或件数。④依数据大小将数据画成柱形。⑤纵坐标之最高点为100%。⑥绘累积线，顺位各项目占全体总数之比率[1]。

3.3 图形生成 在Minitab中选择“统计-质量工具-Pareto图”。

3.4 分析及措施 使用帕累托分析法：先比较偏差影响不良率程度的高低，然后处理影响不良率较严重的项目，并依次采取措施。

3.5 应用实例 以下是我公司2012年偏差产生原因的发现与预防数据统计实例。统计数据见附表4，帕累托图见附图10。

附表4 2012年偏差原因分类表

附图10 2012年偏差产生原因的Pareto图

2012年偏差产生的原因主要涉及设备故障/过程中断、中控项目检查超出标准、未按规定执行、文件记录缺陷、人员操作5个方面。设备故障/过程中断7份（47%）；中控项目检查超出标准3份（20%）；未按规定执行1份（7%）；文件记录缺陷2份（13%）；人员操作原因2份（13%）。

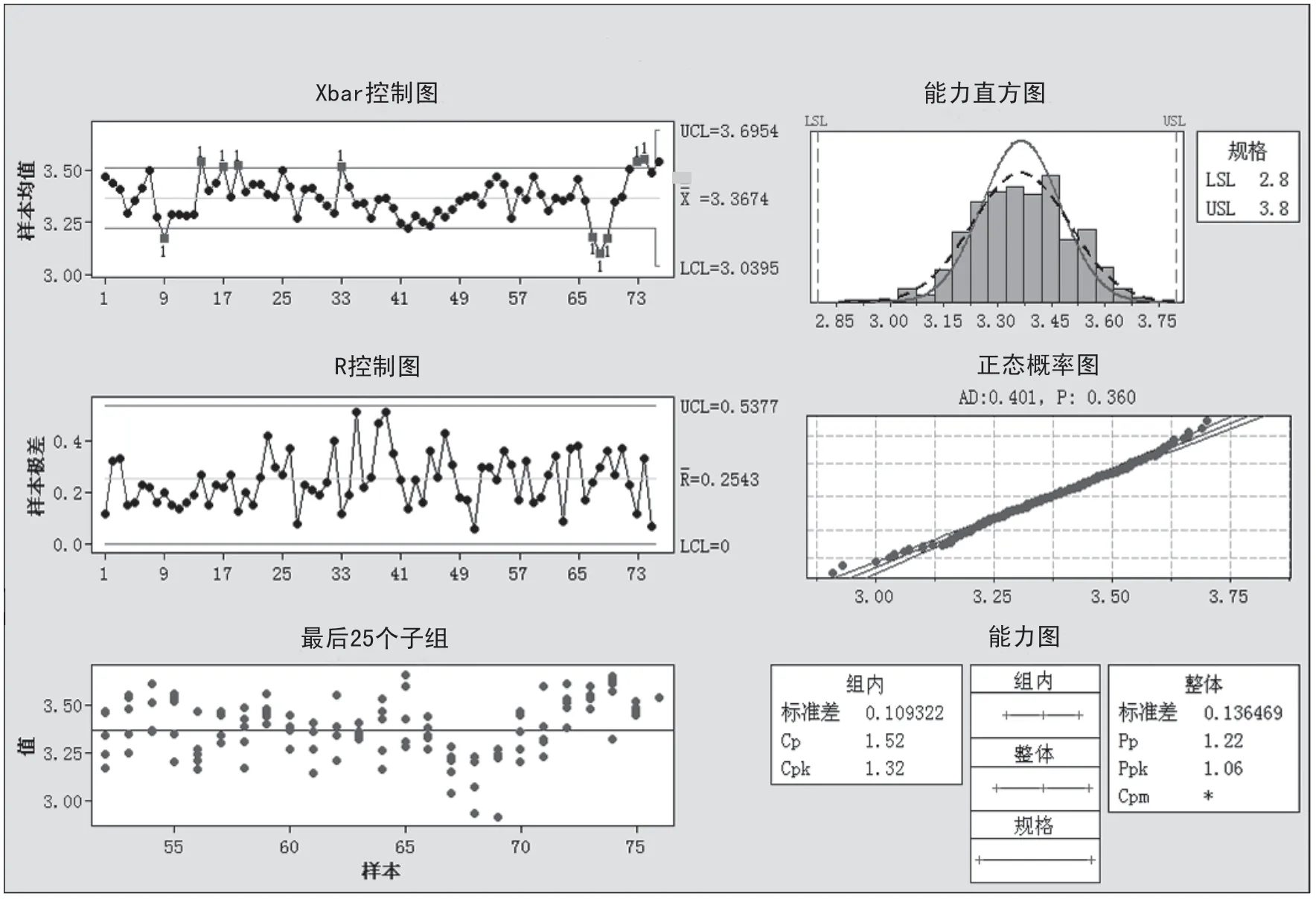
附图11 某产品有效成分数据“六合图”（Capability Sixpack）

评估与措施：2012年因设备故障造成的偏差占47%，是发生偏差的主要原因。分析：随着产品产量不断递增、设备长期使用，现有设备已处在满负荷生产的状态，是导致频繁出现设备故障偏差的重要因素。措施：保证设备留有充足的预防性维护、维修时间，减少设备故障造成的偏差，避免偏差对产品质量产生的影响。制定预防性维护保养计划并实施，防止类似情况发生。其余所有偏差项目（中控项目检查超出标准、未按规定执行、文件记录缺陷、人员操作原因）均根据不良发生率多少依次制定了相应的纠正与预防措施，措施的有效性得到控制和追踪。

4 Minitab能力分析功能在产品的检验结果趋势分析数据统计中的应用

4.1 概述 我公司使用Minitab能力分析功能中的“六合图”（Capability Sixpack）功能，对成品检验结果进行数据分布和趋势分析。六合图包含本文1、2项中的控制图和直方图的功能，且含“正态概率图”、“最后25个子组”、“能力图”。

可以通过控制图和能力直方图以图形化方式评估过程是否受控。正态概率图有助于评估数据的分布特征。能力图还可以计算能力指数PCI，即规格公差占自然过程变异的比率。过程能力指数PCI是评估过程能力的简单方法，由于将过程信息简化为一个数字，因此可使用能力统计量对一个过程与另一个过程的能力进行比较。我公司在年度回顾时用过程能力指数作为考察产品的质量满足质量标准情况的量化指标。

4.2 图形生成 在Minitab中选择“统计-质量工具- Capability Sixpack-正态”。

4.3 图形分析 ①控制图和直方图的分析见本文1、2项中所述；②正态概率图：如显著性P≥0.05，则数据呈正态分布；如显著性P＜0.05，可通过“Box-Cox”变换（使用Minitab进行转换，方法略）使之呈正态后进行Capability Sixpack分析；③能力图：根据国家标准《常规控制图》（标准编号：GB/T 4091-2001），“过程控制与过程能力”中规定：PCI＝（UTL-LTL）/6σ，其中PCI：过程能力指数，UTL：上容差限，LTL：下容差限，σ：平均组内变差。PCI应不小于1.33。在Minitab中，按照PCI计算公式，PCI等同于Cp。

4.4 应用实例 以下是我公司2012年某产品有效成分 数 据“ 六 合图”（Capability Sixpack）统计实例。有效成分含量标准2.8～3.8mg/粒。六合图见附图11。

含量数据统计如下：①Xbar控制图10个点超出3倍标准偏差，但未超过标准2.8～3.8mg/粒，结合能力直方图、正态概率图发现数据分布密集且呈正态（P＝0.360＞0.05），直方图未出现不良模式且远离标准，可以认为超出点为偶然值，不影响总体趋势。②过程能力指数PCI＝Cp＝1.52＞1.33，质量检验结果数据在一年中满足质量标准情况较好。

5 结论

在我公司年度质量回顾中，Minitab应用于关键中间控制点控制、成品的检验结果趋势分析、原辅料质量状况评价、偏差的发现与预防，获得了良好效果，数据、数据组意义分析更科学，趋势更明确，对质量决策有重要指导作用，证明Minitab在制药企业年度质量回顾中的应用是可行的，其数据和结果分析是可靠的。