基于互信息图割的风景图片美学测度

谭云兰，谭 彬

基于互信息图割的风景图片美学测度

谭云兰1,2，*谭 彬1,2

（1. 井冈山大学电子与信息工程学院，江西 吉安 343009；2．同济大学电子与信息工程学院，上海 201804)

提出了一种基于最大互信息图割的摄影照片可计算美学测度算法。该方法按照信息理论元素将彩色图像R/G/B三通道信源空间进行压缩，根据图像邻近位置颜色分布相似的原理，进行区域Bins合并。然后采用逐像素扫描方式，用贪心法以最大信息熵为优化目标，找出区域的分割位置。接着采用二叉分割树进行存储优化分割节点，用大顶堆获取当互信息值最大的节点，对区域反复进行垂直或水平分割，以给定的分割区域块数为终止条件。最后累加分割过程中互信息值最大的节点之和作为照片最终的美学测度值。分割过程中，对算法进行加速，将R/G/B三通道的各像素直方图由16777216个Bins压缩成64个Bins。实验结果表明，这种算法测量的美学值与Ground truth一致，能有效地表现原图像的丰富细节，是一种将信息理论元素在图像微观美学测度的一种尝试。

最大互信息；可计算美学；图像分割；二叉分割树；大顶堆

0 引言

为了使计算机能模拟人类自主地理解、推导和计算“美”的可计算方法，并在相关应用中做出可行性的美学决策，近年来国外兴起了图像可计算美学( computational aesthetics)的研究。Birkhoff[1]最早提出了图像的美学测度是图像的秩序(Order)和复杂度(Complexity)之比的粗糙估计原型，即Measure= Order/ Complexity，但并没有给出具体的数学计算模型。Machado等人[2]通过心理学TDA实验验证了他所提出了美学公式Measure=IC/PC，认为图像的美学度量与图像本身的复杂性( IC)成正比，与人脑处理图像信息的复杂度( PC)成反比。Rigau等人[3]利用信息论的观点和思路拓展了Birkhoff的美学信息度量，给出了结合信息论和Kolmogorov复杂度[4]的美学量化方法，包括利用色彩分布信息计算图像的香农熵来定义的美学测度。目前大部分与图像复杂度相关的美学研究，主要集中在美学测度的直接推导，试图研究利用公式直接对整幅图像计算图像美学测度。Romero[5]统一图像维度和格式，在统一HSV颜色空间V(亮度)通道上抽取图像边缘特征，使用图像JPEG和分形压缩方法估计了图像的复杂度，取得较好的美学测度和分类排序结果，由于计算复杂，并没有在图像的H(色相)，S(饱和度)通道中开展美学测度研究。Marchesotti[6]抽取图像梯度和彩色特征对摄影照片进行美学评估，注重摄影照片的彩色逼真度、色饱和度、彩色平衡、彩色反差等特征抽取，开发了一个通用的基于内容的美学预测描述器，为摄影照片的美学评估提供有益的思路。

互信息量的概念源于信息论，它是两个随机变量统计相关性的一种测度。将互信息应用用于图像分割方面，国内外的学者开展了一些研究。Rigau等人[7]将输入图像X与输出图像Y的分割处理过程看成是一个Markov链过程，以每次分割损失最小MI(Mutual Information)也就是获得最大MI为目标，自顶向下，自左向右逐步处理在亮度通道将图像空间合并成同质区域，设计了一种基于图像亮度通道直方图的图像区域分割方法。吕庆文等人[8]采用基于模拟退火算法和互信息量方法，以互信息熵差作为一种新的分类类数判据为基础，构造了一种新的最大互信息量阈值分割算法。卢振泰等[9]提出了一种新的基于K均值算法与互信息技术相结合的医学图像分割算法，创新性尝试将图像配准方法用于灰度图像分割领域。这三种方法是将灰度图像中在同一范围内的像素灰度值归属于同一类，用一个或几个灰度阈值将图像分割成若干个类，从而实现分割效果，这些研究也仅仅是阐述了在灰度图像上的分割，没有针对彩色图像进行分割。

目前国内中文文献除了文献[10]综述了可计算美学的研究进展，还未见相关论文阐述该领域的研究成果。本文提出了一种基于互信息图割的风景照可计算美学测度算法，利用色彩信息分布合并来计算图像分区的互信息，从而加快了分割速度。分割过程中利用公式计算每个待分割区域的互信息，采用贪心法选出当前分割状态下的最大互信息区域，利用大顶堆找出当前分割过程中互信息值最大区域的分割位置，最后将二叉分割树中的内部节点的互信息值进行相加，从而获得图像的美学测度。

1 基于互信息图割问题描述

1.1 信息理论

1.2 图像分割问题描述

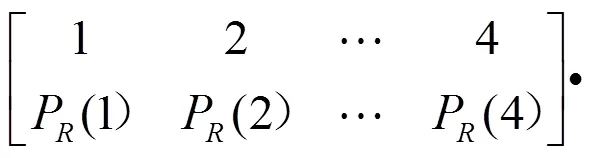
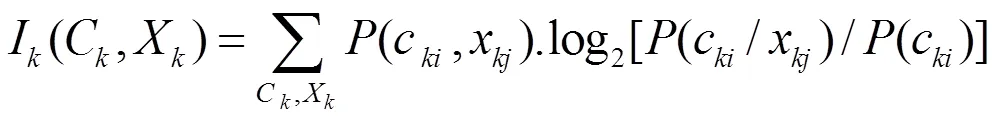
其中C为第K个分割区域类别，X为分割方式，C为第K个区域第i个类别，X为水平或垂直分割。

2 分割算法

以上述信道作为出发点，根据图像邻近位置颜色分布相似的原理，进行区域Bins像素聚类合并。以最大互信息为优化目标，使用贪心算法获取最佳分割位置，以给定的分割区域块数为终止条件进行反复分割。

2.1 统计Bins

对于彩色图像进行分割，其本质就是按照信息理论元素将信源空间进行压缩，将某些位置邻近、大小相近的像素值进行合并，合并后的像素值概率等于合并前各像素值相应概率之和。由于彩色图像R/G/B三通道各像素取值为0-255共256个Bins等级，如果逐个像素的进行三个通道等级统计，则需要统计的等级为256^3= 16777216。为了加快计算速度，得到较佳的合并效果，本算法将0-255区间压缩为4个Bins等级，即取值1,2,3,4。压缩之后三通道的像素取值等级为4^3=64，压缩方法如图1(a)所示，图1(b)是ID.3041056的三通道各bins柱状统计图。

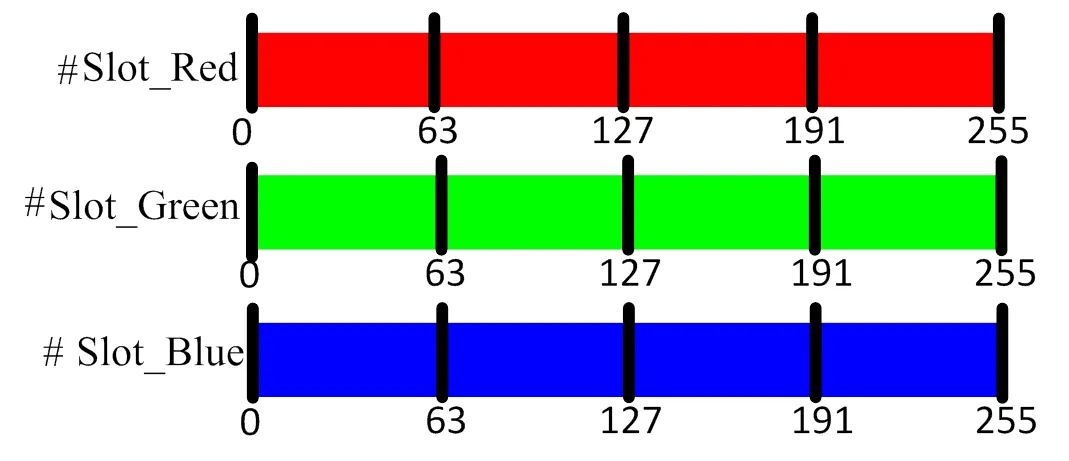
(a) Bins区间压缩图 (b) 压缩后ID.3041056的三通道各bins统计图

(a)Compression of bins for R/G/B channels (b) Bins numbers for R/G/B channels after being compressed over ID.3041056

Fig.1 Bins compression and the corresponding numbers for R/G/B channels

2.2 区域分割信息熵的计算

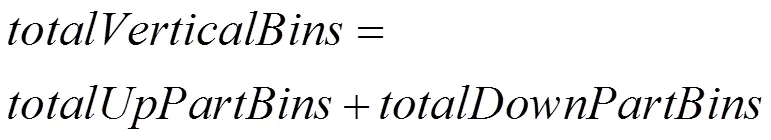
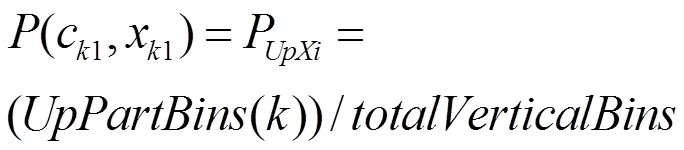
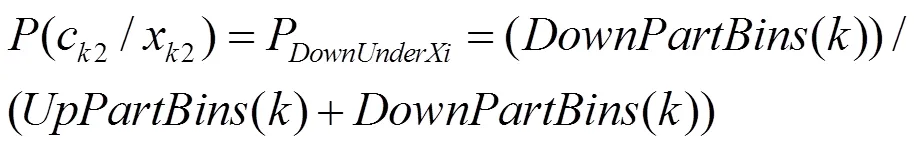
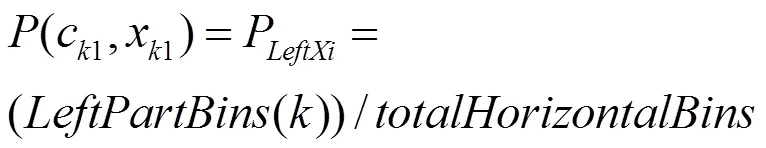
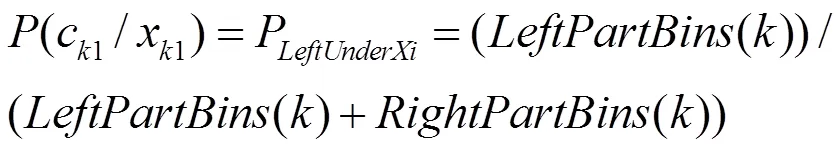
2.3 贪心法分割与二叉分割树构建

整个分割过程中，最重要的就是找出某区域的分割位置。采用逐像素扫描方式，对某分割区域采用水平或垂直方向，计算当前扫描位置左右或上下两部分的信息熵，采用贪心方法找出最大信息熵时位置，作为该区域的分割位置。此外，选出互信息值最大的待分割节点也很重要。由于已分割和未分割的节点都存储在二叉分割树中，若在二叉分割树中查找值最大的未分割节点则比较耗时，而用堆(heap)却可以高效地解决。因此，在每次分割后，将互信息值最大的节点插入大顶堆中，而大顶堆总是存放关键字值最大的未分割节点。在下一次分割时，只取当前堆顶的元素作为分割节点，因此用大顶堆非常容易获取当前分割位置，从而节省了运行时间。

分割开始时，构建空的二叉分割树和堆。分割过程中，首先将根节点Root插入到二叉树和堆中，接下来对根节点进行分割，将分割后的2个节点存贮到二叉分割树中，将互信息最大的节点存储到大顶堆中。下一次分割时从大顶堆中取出当前节点进行分割，分割之后存储到二叉分割树中，同时将互信息最大的节点存储到大顶堆中。反复执行这个过程，直到满足指定的分割区域数为止。图2(a)是ID.3041056分割区域为10的空间二叉分割树，图像的分辨率为369*277。分割过程是先对根节点进行第一次分割，根节点Root的分割位置SeperationPosition=105，分割方式SeperationMode=’Horizontal’；接下来从分割后得到的2个节点0.1265和0.1130中选择值最大的进行分割；以后每次都从当前未分割节点中选择值最大的节点进行分割，经过9次分割之后(分割顺序标识为①-⑨)，分割出10个区域，每个叶子节点代表一个分割区域。图2(b)是按照图2(a)分割过程得到对应的分割位置及互信息值分布效果图。图3是分割块数为100,300,600的分割效果图，设置的分割块数越多，越能拟合原图A细节，从信息论角度来说，这是一种微观美学度描述。

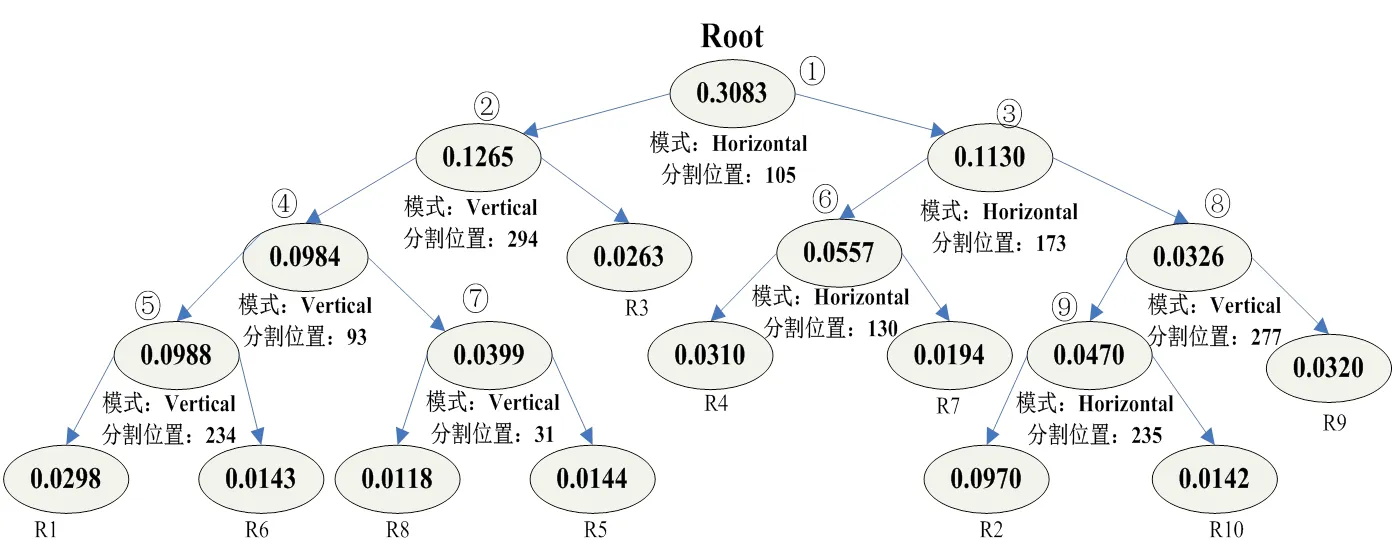
图2 (a) 分割区域为10 的空间二叉分割树 (b) 分割区域为10的分割位置及互信息

图3 A为ID.3041056的原图，B、C、D分别为分割终止条件为100块区域，300块区域和600块区域的分割效果图。

2.4 互信息图割美学测度算法描述

算法1. 互信息图割美学测度算法

输入：待分割的原图像分割的终止条件——分割区域块数

输出：分割效果图，分割图的美学测度值

算法描述：

Step 1 首先统计待分割的图像的压缩成柱状bins。对每个像素，计算其Slot_red, Slot_green, Slot_blue值，根据公式bins(i,j,l,m,n)=bins(i-1,j,l,m,n)+(bins(i,j-1,l,m,n)-bins(i-1,j-1,l,m,n))+1，计算，其中l,m,n=1,2,3,4；

Step 2 构建大顶堆(MaxHeap)和二叉分割树(BinarySeperationTree)。将压缩成柱状bins作为第一个节点，放置在MaxHeap堆顶以及BinarySeperationTree根节点；

Step 6 最后一次分割后，所累加的InformationGain值定义为该图像的美学测度值，同时显示分割效果图。

2.5 时间复杂度分析

根据算法中的各个步骤，算法总的时间复杂度为O(HLength*VLength*Bins^3)+ O(nlogn)+ (n-1)*O(HLength*VLength*Bins^3)，总的空间复杂度为3*n-1+ Bins^3，其中Bins为单通道颜色分段数，n为预设的分割区域块数。Bins统计阶段的时间复杂度为O(HLength*VLength *Bins^3)，所需的存储空间为Bins^3；n个区域分割时构建二叉树分割树的时间复杂度为(n-1)*O(HLength*VLength*Bins^3)，所需存储空间为2*n-1；堆操作阶段的时间复杂度为O(nlogn)，所需存储空间为n。

3 实验结果与分析

本实验数据集采用美国公共摄影照片集网站http://www.photo.net/和dpchallenge网站http://www.dpchallenge.com/中的照片。采用Ritendra Datta[14-15]的Avg. Aesthetics为照片集网站http://www.photo.net/中照片的参考Groundtruth。为了获得更真实有效的美学评估值作为对应ID编号照片的参考Groundtruth，在dpchallenge网站上大量在线照片中，设置下载过滤条件Votes>120。本实验遴选200张照片，由于版面有限，选取其中4副照片的分割效果图，如图4~图7所示。实验硬件环境为内存2M+Duo CPU 2.8GHz的PC机，软件环境为Matlab2011a+C+ Windows7。

3.1 分割效果图

为了体现分割算法的鲁棒性，遴选不同分辨率且All Votes >120的照片进行算法实验。图4~图7中的A为原始照片，B为分割区域终止条件为600块的分割效果图，C为Felzenszwalb[16]的算法分割效果图。

图4 ID.892180的原图及分割效果图

图5 ID.505281的原图及分割效果图

图6 ID.772103的原图及分割效果图

图7 ID.1218468的原图及分割效果图

3.2 实验结果分析

图像分割视为图像的一种退化，本实验以给定的分割区块数为终止条件，在分割过程中以最大互信息量为优化目标，所以可认为所获得的分割是含有最多原图像信息的分割。图4~图7的B都能将照片中的显著性组成部分分割出来。分割过程扑捉了图像的空间要素，分割效果反应了整张照片的各个景观要素。图4~图7的C是Felzenszwalb P F所提出的分割算法效果图，从视觉效果上看，在反应原图的色彩逼真度方面还需要做较多改进，此外在反应原图的细节方面，图4(c)主体对象完整的分割出来。

图4~图6的参考Groundtruth是根据网站注册用户投票各评分等级的加权平均。图4投票数为122，图5投票数为167, 图6照片的投票人数达到504。本文算法的美学测度取值范围为[0-3]，而图4~图6的美学测度取值范围为[1-10]，图7的美学测度取值范围为[1-7]。从图像分割效果来看，所求出的区域和原图像中显著性区域相吻合，这种算法能有效地表现原图像的丰富细节和彩色逼真度。从表1中可以看出，尽管测量尺度不一致，但每幅图所评估的美学测度值大小与Groundtruth一致。分割后图像的信息熵值越大，说明从原图中得到的信息量越大，所获得的最优分割结果包含有原图像的信息量最多，越能体现摄影照片图像的微观美学测度。

表1 美学评估值

4 结束语

由于图像美学度量的主观性和复杂性，且可计算美学测度图像的研究还处于初步探索和萌芽阶段，有大量的问题有待研究，目前为止并没有成熟的方法。本文按照信息理论元素将彩色图像R/G/B三通道信源空间进行压缩，采用图像色彩空间自相似原理，将摄影照片分割成均匀像素区块，采用贪心法以最大互信息量为优化目标，多个实验图片结果表明，所获得的最优分割结果包含有原图像的信息量最多，拟合了原图像的丰富细节，是一种获得含有原图像最多信息的分割,是利用最大互信息在摄影照片可计算微观美学测度领域的一种尝试。今后将进一步研究其它度量摄影照片美学值的方法，但本文算法所计算的值将作为照片的可计算美学度量值之一。

[1] Birkhoff G D. Aesthetic measure[M]. Cambridge, Mass., 1933．

[2] Machado P, Cardoso A. Computing aesthetics[M]. Advances in Artificial Intelligence. Springer Berlin Heidelberg, 1998: 219-228.

[3] Rigau J, Feixas M, Sbert M. Informational aesthetics measures[J]. Computer Graphics and Applications, IEEE, 2008, 28(2): 24-34.

[4] Rigau J,Feixas M,Sbert M. Conceptualizing birkhoff's aesthetic measure using shannon entropy and kolmogorov complexity[C].Proceedings of the Third Eurographics conference on Computational Aesthetics in Graphics, Visualization and Imaging. Eurographics Association, 2007: 105-112.

[5] Romero J, Machado P, Carballal A, et al. Aesthetic classification and sorting based on image compression[M]. Applications of Evolutionary Computation. Springer Berlin Heidelberg, 2011: 394-403.

[6] Marchesotti L,Perronnin F,Larlus D,et al. Assessing the aesthetic quality of photographs using generic image descriptors[C]. Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011: 1784-1791.

[7] Rigau J, Feixas M, Sbert S. An information theoretic framework for image segmentation[C]. Image Processing, 2004. ICIP'04. 2004 International Conference on. IEEE, 2004, 2: 1193-1196.

[8] 吕庆文,陈武凡. 基于互信息量的图像分割[J].计算机学报,2006,29(2):296-301.

[9] 卢振泰,吕庆文,陈武凡. 基于最大互信息量的图像自动优化分割[J].中国图象图形学报,2008,13(4):658-661.

[10] 王伟凝,蚁静缄,贺前华. 可计算图像美学研究进展[J].中国图象图形学报,2012,17(8):893-901.

[11] Cover T M, Thomas J A. Elements of information theory[M]. John Wiley & Sons, 1991.

[12] Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55.

[13] Sethi I K, Sarvarayudu G P R. Hierarchical classifier design using mutual information[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1982 (4): 441-445.

[14] Datta R, Joshi D, Li J, et al. Studying aesthetics in photographic images using a computational approach[M]. Computer Vision–ECCV 2006. Springer Berlin Heidelberg, 2006: 288-301.

[15] Datta R, Wang J Z. ACQUINE: aesthetic quality inference engine-real-time automatic rating of photo aesthetics[C]//Proceedings of the international conference on Multimedia information retrieval. ACM, 2010: 421-424.

[16] Felzenszwalb P F, Huttenlocher D P. Efficient graph-based image segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167-181.

COMPUTATIONAL AESTHETICS MEASURE FOR LANDSCAPE IMAGES BASED ON IMAGE SEGMENTATION OF MUTUAL INFORMATION

TAN Yun-lan1,2，*TAN Bin1,2

(1. College of Electronic Information and Engineering,Tongji University,Shanghai 201804,China;2. School of Electronic Information and Engineering,Jinggangshan University,Ji’an,Jiangxi 343009,China)

An algorithm for computational aesthetics measure of photographs based on image segmentation of mutual information is proposed. Using the information theory elements, information source space (ISS) of the color image R/G/B channels is compressed. Regional bins are combined according to the principle of the image colors spatial self-similarity distribution to the neighboring location. During the partitioning, the maximum mutual information of all the nonterminal nodes stored into the binary partitioning tree is calculated, which is added as the aesthetics measure value for photographs. Also, the algorithm is accelerated. Each pixel R/G/B three-channel histogram of 16,777,216 Bins is compressed into 64 Bins and the operation of getting the split position of the current node with max-heap is executed. Experimental results show that the values ​​of aesthetic quantified by the algorithm are consistent with the Ground-truth and the segment result can effectively represent the rich detail from the original image.

the maximization of the mutual information; computational aesthetics measure; image segmentation; binary space partition tree; maxheap

TN911.73

A

10.3969/j.issn.1674-8085.2014.06.012

1674-8085(2014)06-0054-07

2014-08-12；

2014-10-27

十二五国家科技支撑计划项目子课题(2012BAC11B01-04)

谭云兰(1972-），女，江西新干人，副教授，博士生，主要从事虚拟现实、图形图像处理研究(E-mail:tanyunlan@163.com);

*谭 彬(1982-），女，湖南常宁人，讲师，博士生，主要从事信号处理，图像处理研究(jatanbin@163.com).