基于字级表示的多输出MPRM电路极性转换算法

卜登立，朱 平

基于字级表示的多输出MPRM电路极性转换算法

卜登立1,2，朱 平1

(1. 井冈山大学电子与信息工程学院，江西 吉安 343009；2. 同济大学电子与信息工程学院，上海 201804)

针对多输出MPRM（Mixed-Polarity Reed-Muller）电路的极性转换问题，提出了使用系数矩阵在字级表示多输出布尔函数及其MPRM，并给出了一种极性转换算法。实验结果表明，与位级表示相比，所提出的基于字级表示的极性转换算法可显著缩短多输出MPRM电路的极性转换时间。

多输出布尔函数；混合极性Reed-Muller电路；极性转换；字级表示；系数矩阵

0 引言

布尔函数既可以在操作域使用基于AND/OR的形式表示，也可以在功能域使用基于AND/XOR的形式表示，前者常称为布尔逻辑，后者常称为RM(Reed-Muller)逻辑[1]。与布尔逻辑实现的电路相比，采用RM逻辑能够减少逻辑门及其内部互联的数量，并且可以减少最大路径长度，因此，人们常用RM实现算术逻辑、通信系统和差错校验等电路[1-3]，并且使用RM逻辑实现的电路具有较好的可测性[4]，能够降低测试复杂度。由于可逆电路和量子电路将XOR门作为基本的构建逻辑，因此RM逻辑在可逆电路和量子电路中也得到了广泛的应用，并且量子电路的综合方法已经开始使用RM逻辑形式[5]。

布尔函数有两种常见的RM展开，固定极性RM(Fixed-Polarity RM，FPRM)展开和混合极性RM(Mixed-Polarity RM，MPRM)展开[1-3]。与FPRM相比，MPRM由于具有更大的极性空间，能够得到更为简化的表示形式，并且由于实际应用中多为多输出电路，因此近年来多输出MPRM电路得到了更多的关注[1, 3]。极性转换是MPRM电路极性优化过程中的一个重要步骤[1,3]，极性转换速度的快慢将影响整个优化过程的性能[3]，因此极性转换方法成为RM电路研究领域一个较为重要的研究方向，如文献[1]中的多输出列表技术和文献[3]中的系数矩阵变换极性转换方法。但是当前的极性转换方法主要是针对位级表示的多输出布尔函数及其MPRM，而字级表示作为逻辑综合领域中一种非常重要的方法与手段[6]，便于对多输出电路进行整体操纵，从而满足并行处理、模拟和验证的要求[6]。近些年来矩阵表示在逻辑电路的设计、可靠性分析以及布尔网络的控制等领域得到了广泛的应用。如文献[7,8]使用矩阵描述逻辑门和逻辑电路的概率行为以及确定性行为，通过矩阵运算来计算逻辑电路的信号可靠度，对逻辑电路的可靠性进行评估。文献[6]和[9]使用矩阵的张量积来计算布尔差分，而布尔差分又被应用在电路可靠性分析[9]、测试、功耗估计等[6]领域。但这些应用或者是使用矩阵在位级表示布尔函数，或者是使用矩阵在操作域表示布尔函数。由于MPRM是在功能域表示布尔函数，因此有必要结合字级表示以及矩阵表示对多输出MPRM电路进行研究。

本文采用系数矩阵在字级表示多输出布尔函数及其MPRM，重点研究多输出MPRM电路的极性转换，给出了一种极性转换算法，并通过实验验证了算法的有效性。

1 多输出布尔函数及其MPRM的字级表示

式(1)所示的形式为多输出布尔函数的位级表示，而字级表示则根据按位计数系统原理[6]，给每个输出函数赋予一个权重，从而将多输出函数表示为字级的算术表达式[6]，如式(2)所示。

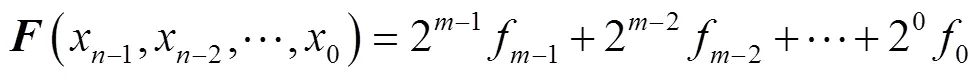
例1一位全加器的位级表示如式(4)所示，其字级表示如式(5)所示。

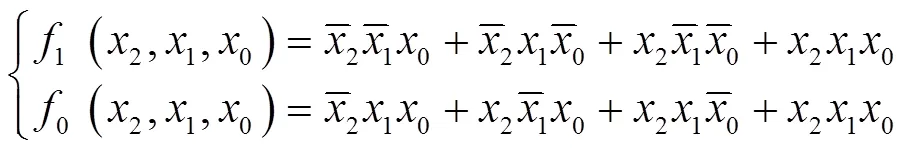
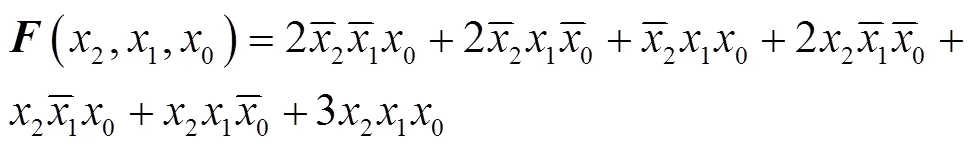
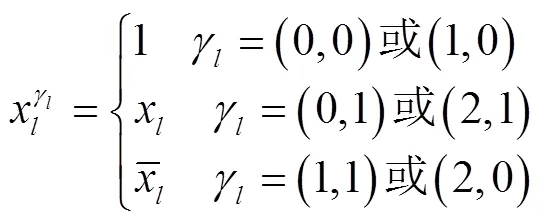
2 多输出MPRM电路极性转换算法

采用字级表示后，可以很方便地对多输出布尔函数进行整体极性转换，从而得到不同极性值的MPRM电路。在得到多输出MPRM电路的字级表示后，再根据每个输出的位置进行屏蔽操作[6]即可得到其位级表示。本文采用文献[3]中的系数矩阵变换方法对字级表示的多输出布尔函数进行MPRM极性转换。

算法1基于字级表示的多输出MPRM极性转换算法

else

end if

else

end if

end if

end while

下面举例来说明字级表示时多输出MPRM电路的极性转换过程。

例2 一位全加器极性值为26的MPRM的字级表示如下式所示，

现使用算法1得到其极性值为5的MPRM。

图1 的极性: 2à0

图2 x1的极性: 2à1

结合式(7)，可得一位全加器极性值为5的MPRM的字级表示为：

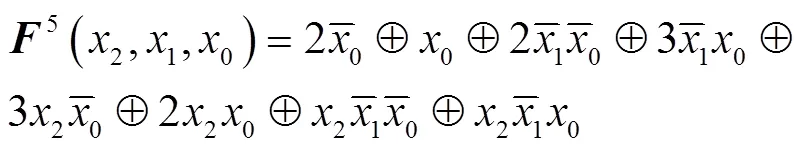
3 实验及结果分析

为验证文中的算法1，并与采用位级表示的MPRM极性转换方法比较，本文还设计了采用位级表示的系数矩阵变换MPRM极性转换算法，称之为算法2，2种算法均使用C++实现，并选取14个多输出MCNC基准电路对2种算法进行测试。测试方法是对每个电路随机生成200个不同的极性值，并按照生成的顺序进行极性转换，记录每一次极性转换所花费的时间，并统计200次极性转换的平均时间。

算法测试的软件环境为Windows XP Professional操作系统，硬件环境为Pentium IV 2.8GHz CPU 512MB RAM。表1给出了所采用的基准电路名称、基准电路的输入数、输出数、200次极性转换的平均时间、字级表示相对于位级表示极性转换时间缩短的比例。

表1 MCNC基准电路测试结果

从表1中的结果可以看出，相对于位级表示，采用字级表示使得极性转换的时间有较大程度的降低。由于矩阵本身的特性，在相同输出的情况下，性能提升的程度随输入数的增加而增加；在相同输入的情况下，性能提升的幅度随着输出数的增加而增大。总体来看，输出数相对越多，则性能提升的幅度也相对越大，如电路misex3、table3和table5，其输出数均大于10，因此性能提升超过了90%。14个电路的平均时间缩短了92%，从而验证了文中所提出的基于字级表示的MPRM电路极性转换算法的有效性。

4 结束语

由于采用RM逻辑实现的电路在面积和可测性方面的优势，使得RM逻辑在数字电路中得到了广泛的应用，并且多输出MPRM电路得到了较多的关注。本文使用系数矩阵在字级表示多输出布尔函数及其MPRM，给出了基于字级表示的多输出MPRM电路极性转换算法。实验结果验证了所提出算法的有效性，相对于位级表示，使用字级表示可以显著缩短多输出MPRM电路极性转换的时间。

[1] 李辉, 汪鹏君, 王振海. 混合极性列表技术及其在MPRM电路面积优化中的应用[J]. 计算机辅助设计与图形学学报, 2011, 23(3): 527-533.

[2] Tan E C, Yang H. Optimization of fixed-polarity Reed-Muller circuits using dual-polarity property[J]. Circuits, Systems, and Signal Processing, 2000, 19(6): 535-548.

[3] 卜登立, 江建慧. 使用系数矩阵变换极性转换的MPRM电路面积优化[J]. 计算机辅助设计与图形学学报, 2013, 25(1): 126-135.

[4] Rahaman H, Das D K, Bhattacharya B B. Testable design of AND-EXOR logic networks with universal test sets[J]. Computers and Electrical Engineering, 2009, 35(5): 644-658.

[5] Drechsler R, Finder A, Wille R. Improving ESOP-based synthesis of reversible logic using evolutionary algorithms[J]. Lecture Notes in Computer Science, 2011, 6625:151-161.

[6] Yanushkevich S N, Miller D M, Shmerko V P, et al. Decision diagram techniques for micro- and nanoelectronic design handbook[M]. Boca Raton: CRC Press, 2006.

[7] Krishnaswamy S, Viamontes G F, Igor L. Markov, et al. Probabilistic Transfer Matrices in Symbolic Reliability Analysis of Logic Circuits[J]. ACM Transactions on Design Automation of Electronic Systems, 2008, 13(1): 8:1-8:35.

[8] 卜登立. 基于伪门故障模型的PTM可靠度评估方法[J]. 井冈山大学学报:自然科学版, 2012, 33(6): 56-60.

[9] Li H, Wang Y. Boolean derivative calculation with application to fault detection of combinational circuits via the semi-tensor product method[J]. Automatica, 2012, 48(4): 688-693.

WORD LEVEL REPRESENTATION BASED POLARITY CONVERSION ALGORITHM FOR MULTI-OUTPUT MPRM CIRCUITS

BU Deng-li1,2,ZHU Ping1

(1. School of Electronics and Information Engineering, Jinggangshan University, Ji’an Jiangxi 343009, China; 2. School of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

Word level representation of multi-output Boolean function and its mixed-polarity Reed-Muller (MPRM) using coefficient matrix is proposed for polarity conversion of multi-output MPRM circuits. Based on this representation, a polarity conversion algorithm is presented. Experimental results show that, in comparison with bit level representation, the proposed word level representation based polarity conversion algorithm can significantly reduce the time consumed for polarity conversion of multi-output MPRM circuits.

Multi-output Boolean function; mixed-polarity Reed-Muller circuit; polarity conversion; word-level representation; coefficient matrix

TP391.72

A

10.3969/j.issn.1674-8085.2014.06.013

1674-8085(2014)06-0061-05

2014-06-12；

2014-10-13

国家自然科学基金项目(61363014)

*卜登立(1975-），男，河北定州人，副教授，博士生，主要从事VLSI设计和可靠性评估、计算机辅助设计方面研究(Email: bodengli@163.com);

朱 平(1955-），男，上海人，教授，硕士，主要从事算法分析与设计方面研究(Email:zhuping810@163.com).