S3到CP4中的常曲率等变极小浸入

艾小梅，章慧芬，朱先阳

3到4中的常曲率等变极小浸入

*艾小梅1，章慧芬2，朱先阳1

(1.井冈山大学数理学院，江西，吉安 343009; 2. 揭阳职业技术学院师范教育系，广东，揭阳 522000)

研究常曲率的3维球面3到复射影空间4中的等变极小浸入，研究结果表明这种浸入只能是弱Lagrangian浸入，从而是全测地的。

复射影空间；等变；弱Lagrangian子流形；极小浸入

远在19世纪60年代开始，许多学者对Kähler流形中的Lagrangian子流形（或称全实子流形）进行了研究，并取得了极大的成果。Bolton J,[1]等人在研究复射影空间CP 中的极小2-球面2中，发现2中的Lagrangian极小2一定是全测地的。随后，陈邦彦[2]对Kähler流形的Lagrangian子流形的几何性质作了归纳，Lagrangian子流形的存在性和唯一性已有了很完美的结论。文[2]还指出，CP中常曲率的Lagrangian极小球面S必是全测地的。

黎镇琦和陶永芊[5]研究了常曲率的3维球面3到3中的极小浸入，最终得到了3中等变的Lagrangian极小3维球面3的完全分类和解析表达式。文中利用等变映射的性质，指出除全测地的3外，只有唯一的一个等变Lagrangian极小3，而陈邦彦在文[2]中把它称为“怪球面”(exotic sphere)。在上述基础上，黎镇琦和周燕飞[6]研究了3维球面3到4中的等变极小浸入，依次得到了4中非常曲率和常曲率的等变弱Lagrangian极小3维球面3的完全分类和解析表达式。

在文[6]中讨论4中等变极小3的一种特殊情形：弱Lagrangian浸入，并得到了这种情形下极小3维球面3的完全分类和解析表达式。在文[6]的基础上，本文针对其一般情形，讨论4中常曲率的等变极小3除了弱Lagrangian浸入的这种情形外，还有没有其他形式的浸入。研究结果表明：不存在其他形式的浸入，只能是弱Lagrangian浸入，从而得到了下面的定理。

1 等变浸入的基本公式

外微分(1.1)可得

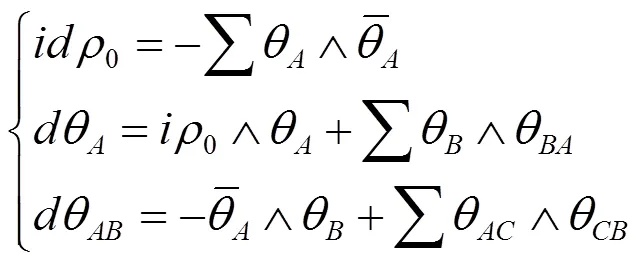
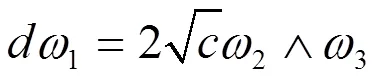
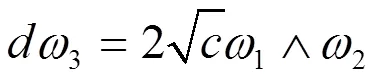
在(1.1)中，可设

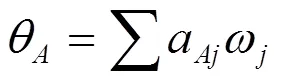
其中

将(1.4)，(1.5)代入(1.2)第1式，由(1.3)得

因此

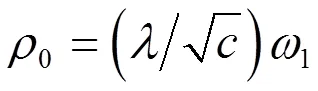
设

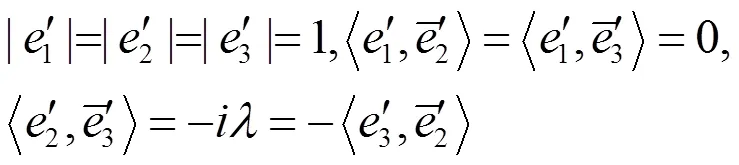
令

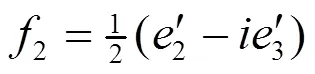
则由(1.9)式知

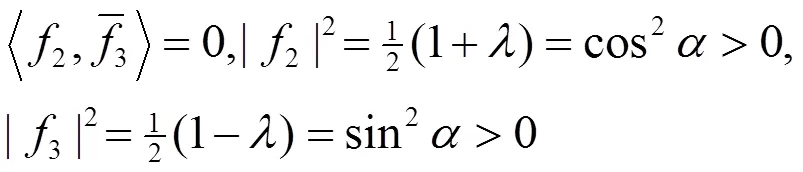
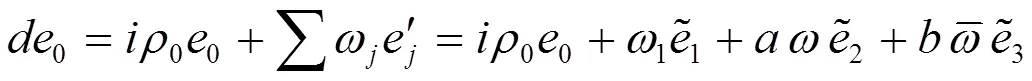
其中

这样就证明了下面的引理1。

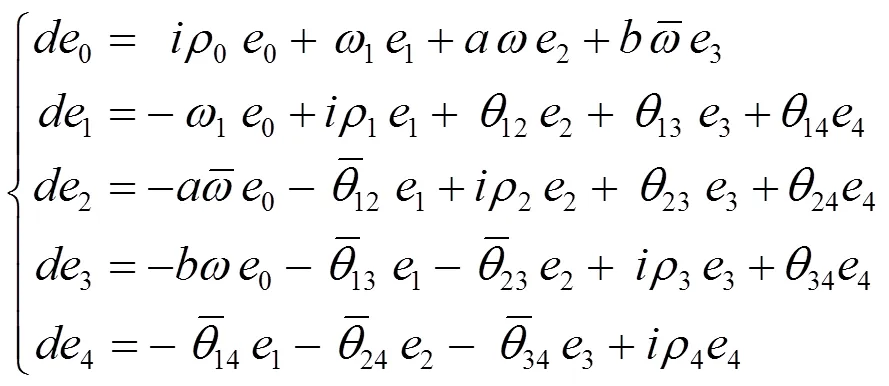
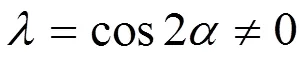
2 定理的证明

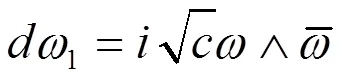
来定义，则由(1.3)可得

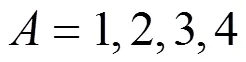
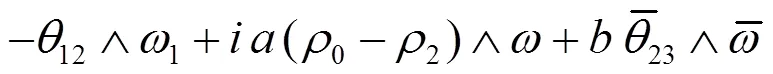
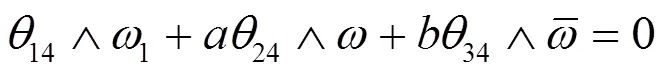
分别取(2.4)和(2.6)的复共轭，得

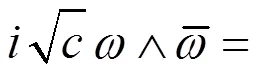
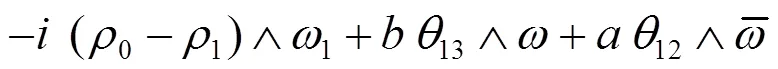
(2.9)

(2.4)和(2.8)等价于

(2.5)和(2.6)等价于(2.5)和(2.9)，也等价于

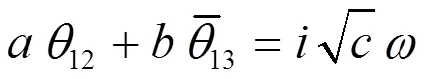
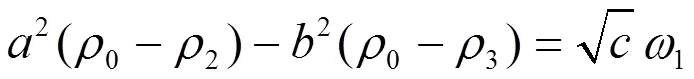
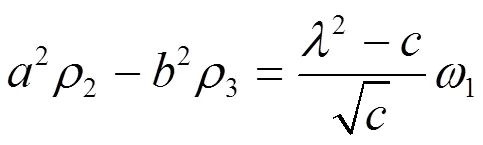
设

从而

代入(2.10)第2式得

因此

再设

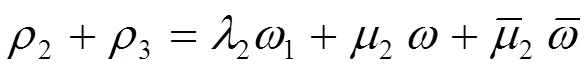
故可设

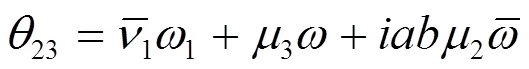
利用(2.19)，由(2.13)和(2.18)解出

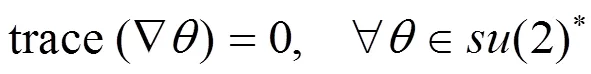
因为

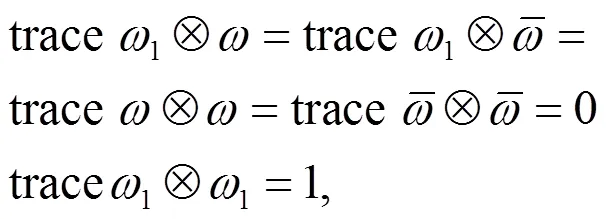
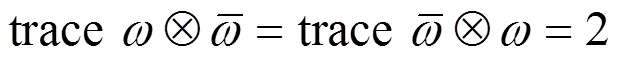
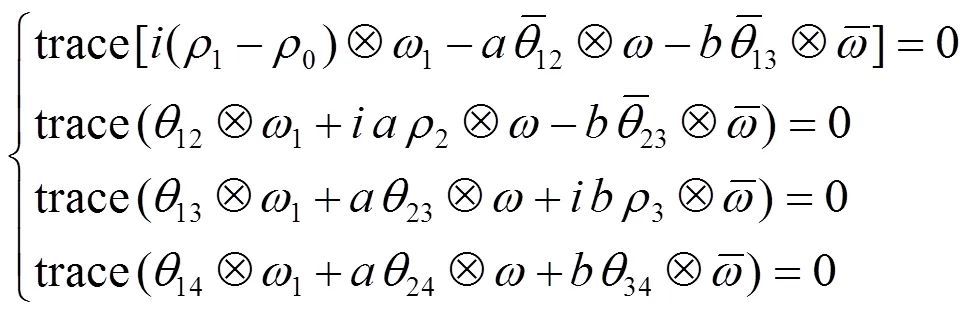
于是由(2.15)，(2.17)~(2.20)，有

代入前面的式中，有

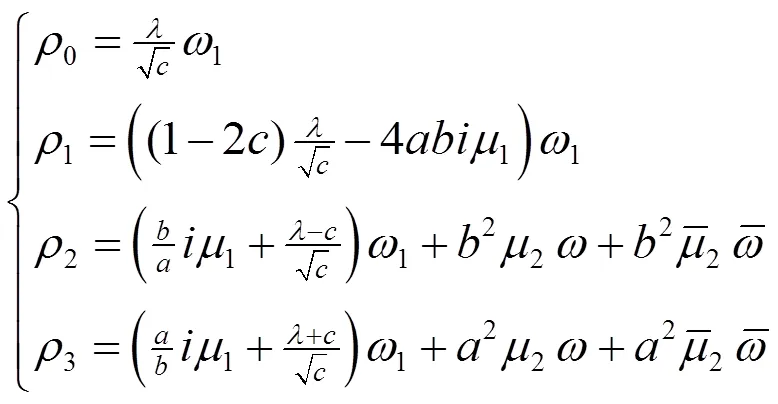
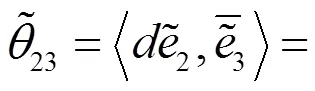
故可设(2.26)和(2.27)中

设

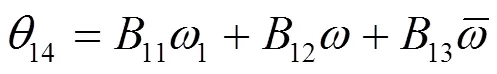
代入(2.7)得

故可设

(1.2)的第3式给出第二结构方程和Ricci方程

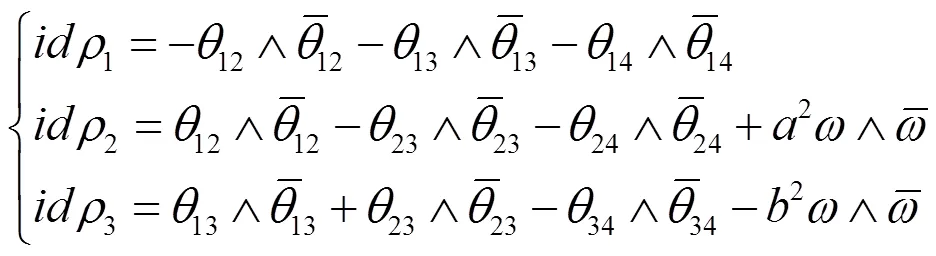
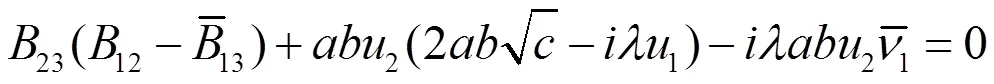
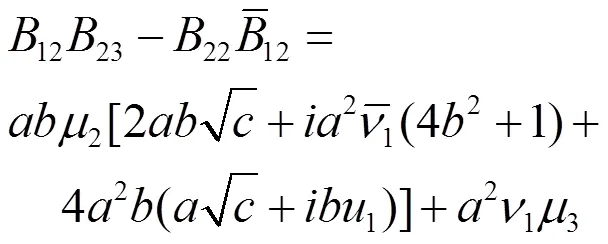
将(2.26)，(2.27)，(2.32)代入(2.35)得

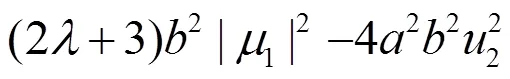
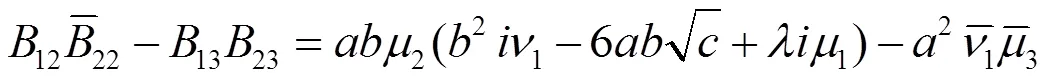
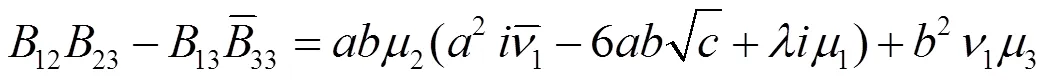
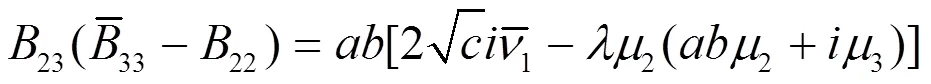
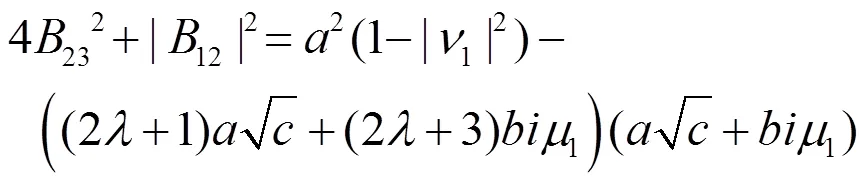
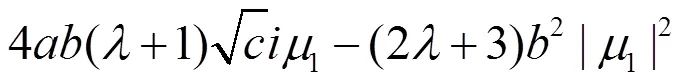
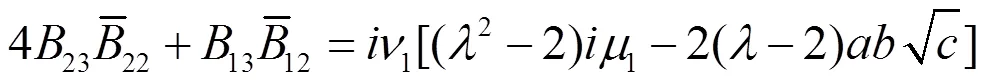
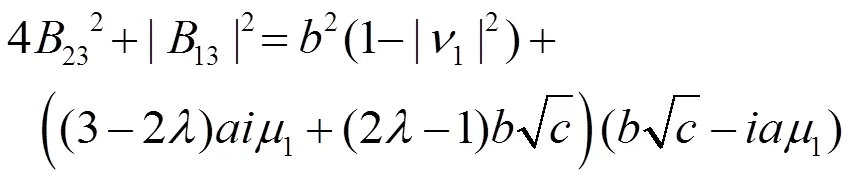
则(2.51)和(2.38)一样。

将(2.53)代入(2.25)得

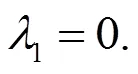
将(2.43)与(2.46)相减得(2.37)。将(2.43)与(2.46)相加得

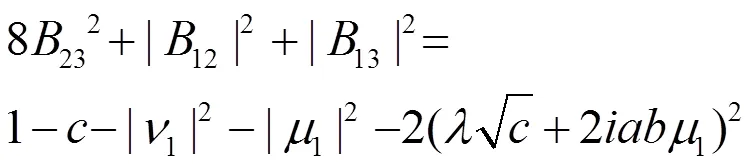
故

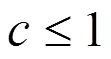
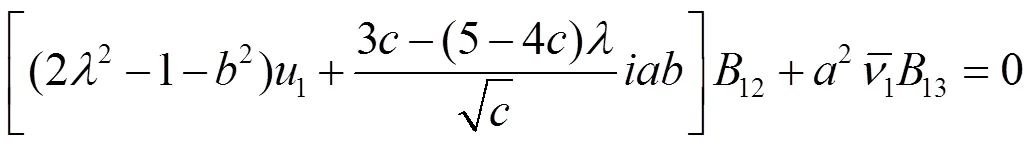
取(2.58)的复共轭，由(2.56)得

用(2.60)减(2.59)得

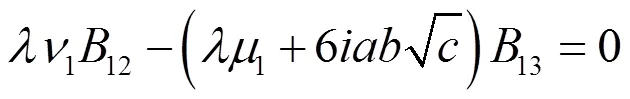
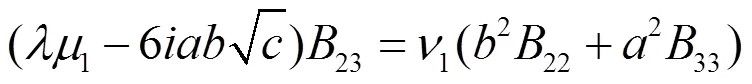
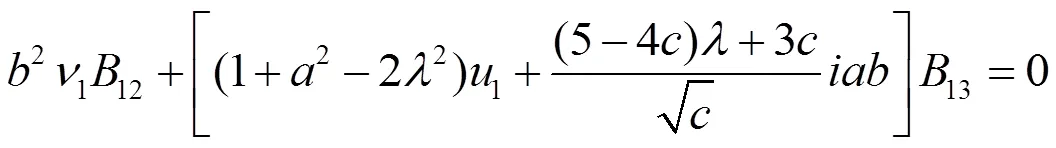
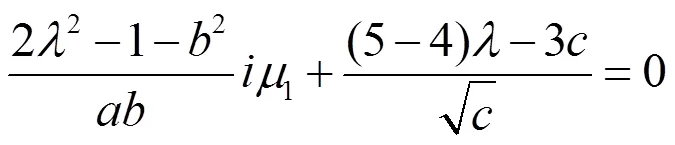
从而由(2.61)，

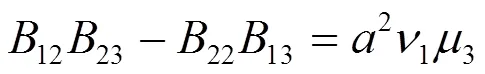
两式相加得

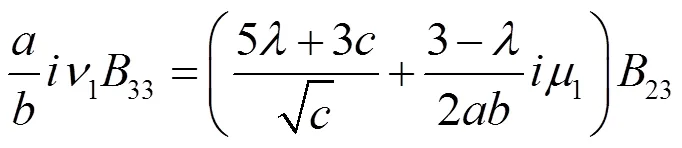
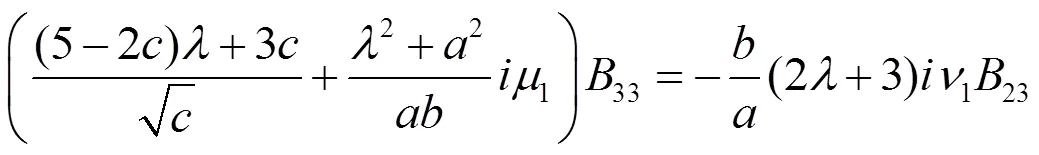
同理，由(2.71)，(2.72)得

将上面两个式子相加，相减可得

(2.56)和(2.82)给出

代入(2.81)得

将(2.83)第1式和(2.84)代入(2.83)第2式得

即有

将(2.83)第1式代入(2.71)，(2.73)得

将(2.83)第1式代入(2.44)，(2.47)，利用(2.78)得

首先，由(2.49)可知

从而由(2.44)，

由(2.26)，(2.27)，此时可设

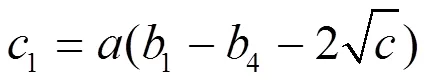
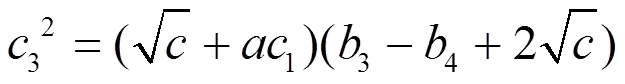
由(2.94)，(2.96)和(2.99)得

由(2.95)，(2.98)，(2.100)和(2.97)得

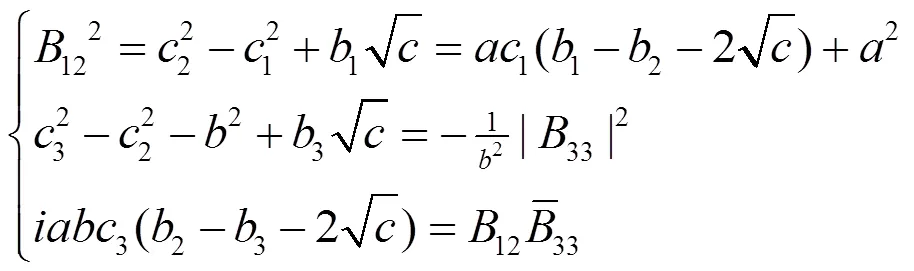
由(2.94)和(2.101)得

代入(2.94)第2式，得

即有

代入(2.94)第3，4式得

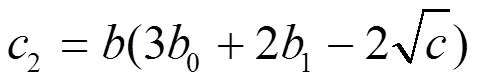
将(2.107)代入(2.105)得

，

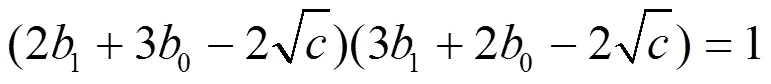
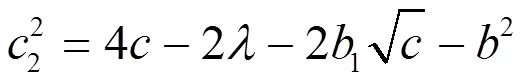
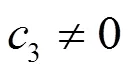
结合(2.106)第2式和(2.115)得

由(2.106)第1式和(2.105)第2式得

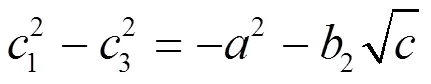
将这三个式子相加，利用(2.107)(2.110)(2.111)化简得

由极小条件(2.24)第1式有：

将(2.110)代入(2.119)，

将（2.109）代入（2.120），得

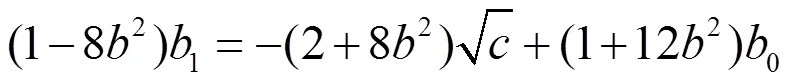
将（2.123）代入（2.124）得，

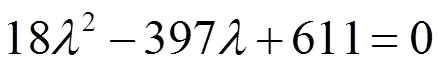
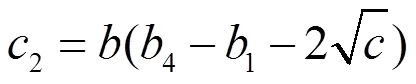
由(2.94),(2.95)和(2.100)得

由(2.96),(2.97),(2.98)和(2.99)得

由(2.94)和(2.126)得

代入(2.94)第2式，得

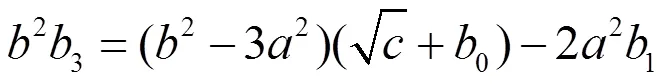
即有

代入(2.94)第3,4式，得

将(2.132)代入(2.130)，得

另一方面由(2.130)得

由(2.129)和(2.134)得

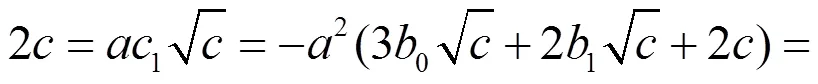
左右相减，得

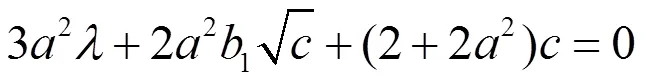
将(2.138)代入(2.137)得

用(2.138)和(2.140)相减得

将(2.143)代入(2.142)得

从而有

将(2.143)与 (2.145)代入 (2.142)得

结合(2.130)第2式和(2.148)得

由(2.130)第1式和(2.129)第2式得

将上面三个式子相加，利用(2.25),(2.134)和(2.135)化简得

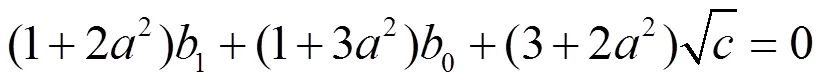
由(2.149)和(2.130)第1式，利用((2.94)有

由(2.94)第4式和(2.122)得

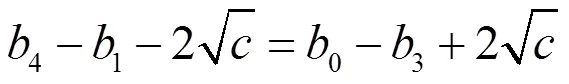
再联合和(2.132)得

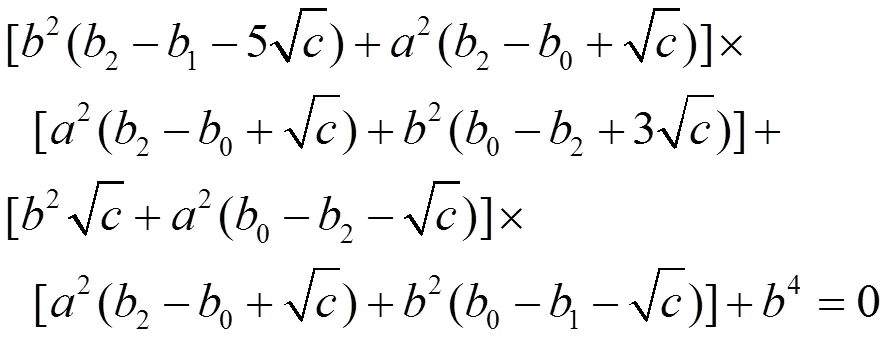
即有

利用(2.129)的第1式

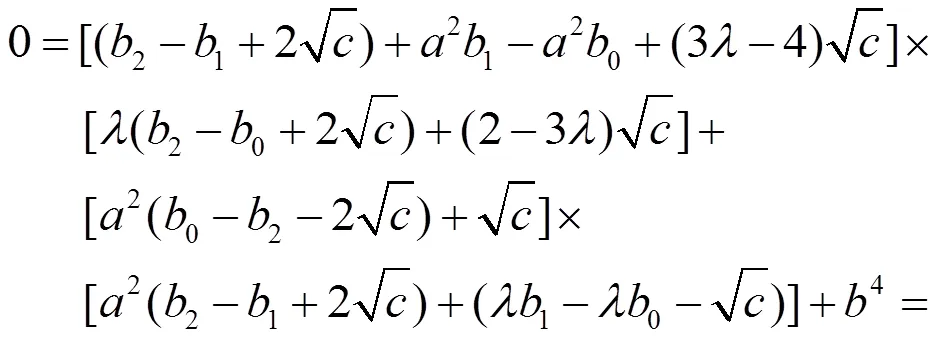
即有

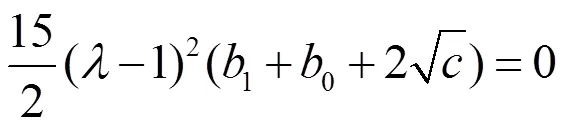
因此

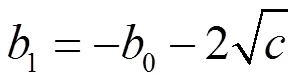
将(2.156)代入(2.135)得

[1] Bolton J, Jensen G R, Rigoli M,et al. On Conformal Minimal Immersion of2intoCP[J]. Math. Ann., 1988, 279(4):599-620.

[2] Chen B Y, Riemannian Geometry of Lagrangian Submanifolds[J]. Taiwanese J. Math, 2001,5(4):1-35.

[3] Li ZQ. Minimal3with constant curvature inCP[J]. J. London Math. Soc., 2003,68(1): 223-240.

[4] Li ZQ, Huang A M. Constant curved minimal CR 3-spheres inCP[J].J. Aust. Math. Soc., 2005, 79(1):1-10.

[5] Li ZQ, Tao YQ. Equivariant Lagrangian minimal3in3[J]. Acta Math. Sinica, 2006,22(4):1215-1220.

[6] 黎镇琦,周燕飞.3到4中的等变弱Lagrangian极小浸入[J].南昌大学学报,2005, 29(5):409-415.

[7] 艾小梅,黎镇琦.3到3中的等变极小浸入[J].南昌大学学报:理科版,2007,31(3): 214-218.

Constant Curvature Equivariant Minimal Immersion from3into4

*AI Xiao-mei1, ZHANG Hui-fen2,ZHU Xian-yang1

(1.School of Mathematics, Jinggangshan University, Ji’an, Jiangxi 343009, China;2. Normal Education Department of Jieyang Vocational and Technical College, Jieyang, Guongdong 522000, China)

complex projective space; equivariant; Lagrangian submanifold; minimal immersion

O186

A

10.3969/j.issn.1674-8085.2014.06.002

1674-8085(2014)06-0004-11

2014-07-06；

2014-09-23

井冈山大学科研基金项目(JZ1307)

*艾小梅(1981-)，女，江西永丰人，讲师，硕士，主要从事微分流形子流形研究(E-mail:37653677@qq.com);

章慧芬(1982-)，女，江西进贤人，讲师，硕士，主要从事微分流形超曲面研究(E-mail:605394651@qq.com);

朱先阳(1969-)，男，湖南湘潭人，副教授，博士，主要从事泛涵微分方程，凸几何分析方面的研究(E-mail:375766879@qq.com).