时标上二阶动力方程有解的充分条件

王志伟，邓志云，杨云苏

时标上二阶动力方程有解的充分条件

*王志伟，邓志云，杨云苏

(井冈山大学数理学院，江西，吉安 343009)

研究时标上的一类二阶非线性动力方程解的存在性。利用riccati变换和Banach空间的不动点定理得到了该类方程存在解的几个充分条件。

二阶动力方程；振动性；时标

0 引言

本文考虑时间测度链上二阶非线性动力方程

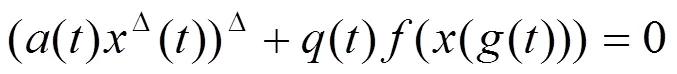
在文中假设：

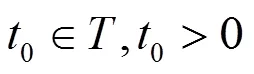
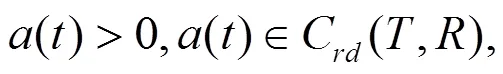
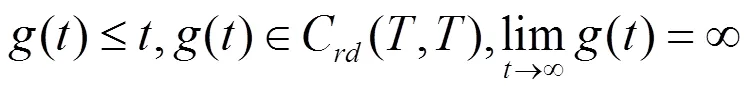
时标上动力方程的研究是由Stefan Hilger开始的[1]。目前，这一理论正得到快速发展[1-5]。在文[2-3]中，讨论了二阶非线性动力方程振动解的存在性；在文[4]中，讨论了二阶非线性动力方程解的振动准则；在文[5]中，利用Lebesgue控制收敛定理得到该类方程的有界解振动的一个充分必要条件。本文通过riccati变换，并借助时标上的相关理论，得到了该方程振动的充分条件；再利用 Banach空间的不动点定理得到该方程有界最终正解的充分条件。

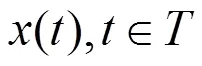
1 预备知识

定义1.1[6]设为实数集的任意非空闭子集，则称为一时标。例如实数集，整数集，自然数集都是时标；但有理数集，无理数集，复数集C，开区间(1,2)都不是时标。

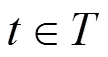
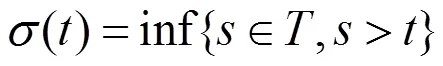
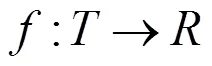
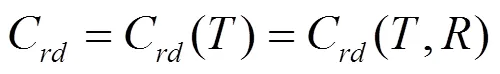
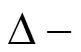
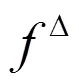
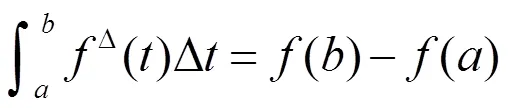
2 主要结果

定理2.1 如果方程（0.1）满足条件(1)，(2)，(3)，设

则方程（0.1）是振动的。

由方程（0.1）及条件(ii)，有

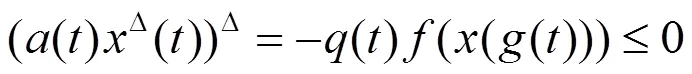
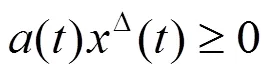
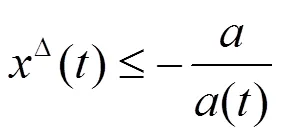
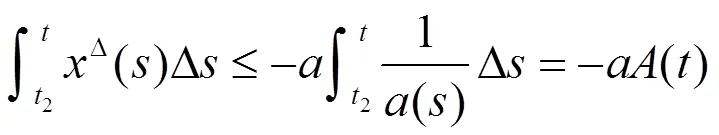
即

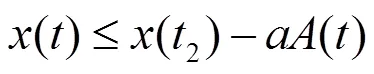
(2.3)

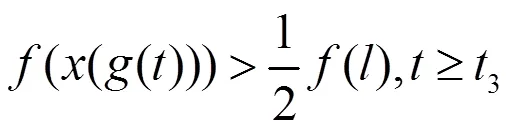
将(2.4)代入(0.1)得到

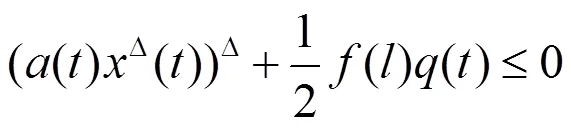
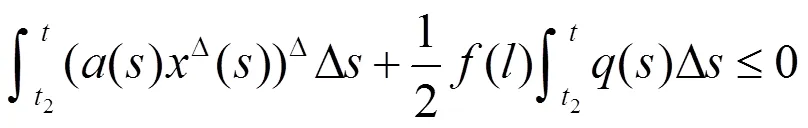
即

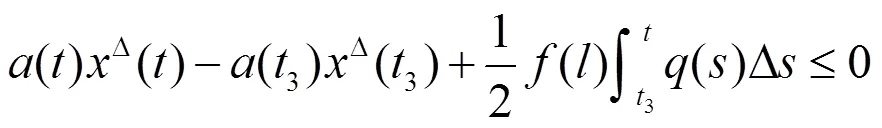
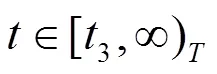
利用（2.1）及上式得

与定理条件(i)矛盾。

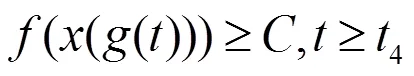
将（2.6）代入（0.1）得到

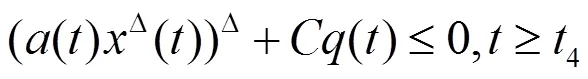
注意到（2.7）与（2.5）的类似，因此，利用类似的讨论可以得到与定理的条件(i)的矛盾。证毕。

定理2.2 如果方程（0.1）满足条件（1），（2），（3），设

则方程（0.1）的一切有界解振动。

利用与定理1证明中相同的讨论，得到不等式（2.5），因此

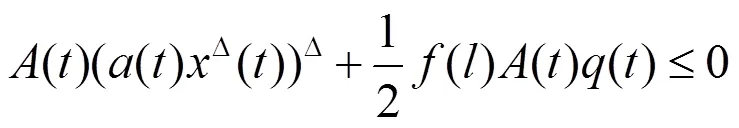
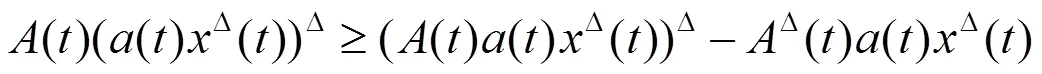
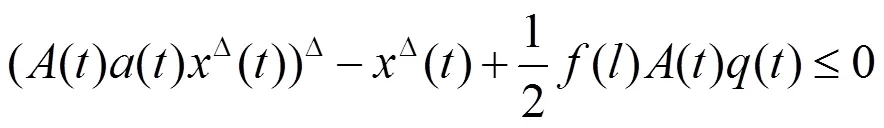
从而有

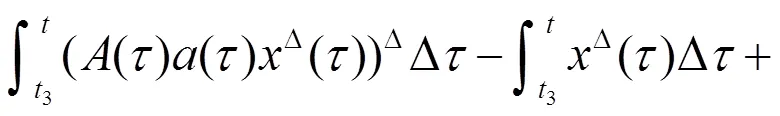
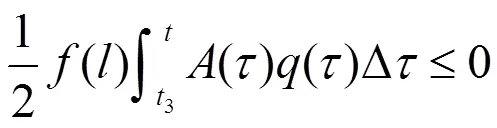
由上式推知

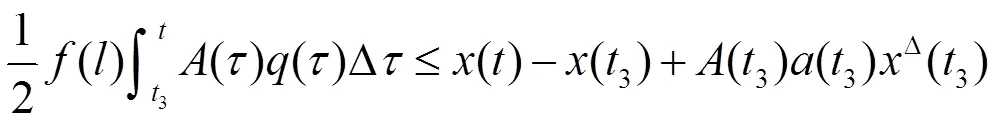
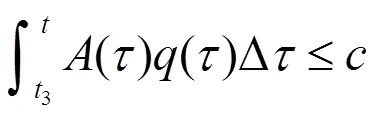
与定理条件(i)矛盾，证毕。

定理2.3 如果方程（0.1）满足条件（1），（2），（3），设

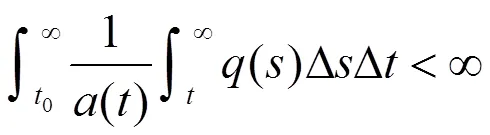
则方程（0.1）存在有界的最终正解。

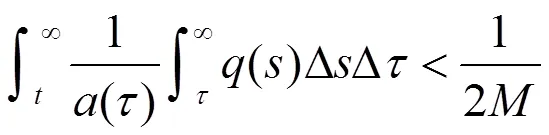
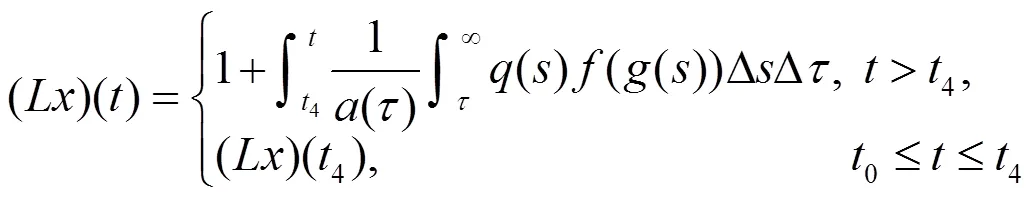
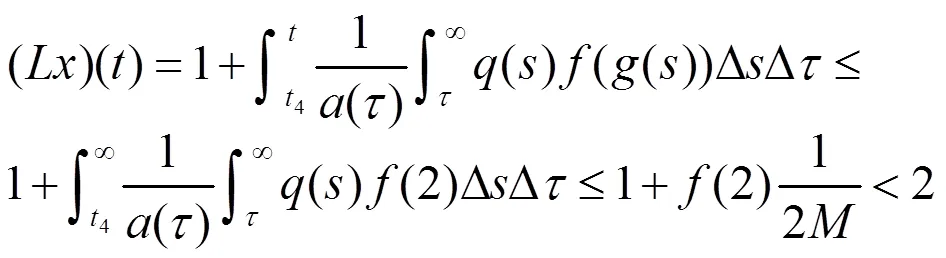
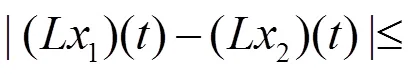
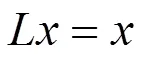
可得

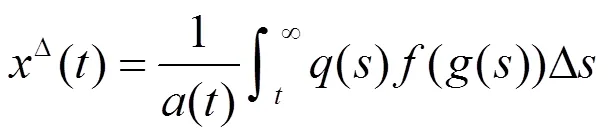
从而

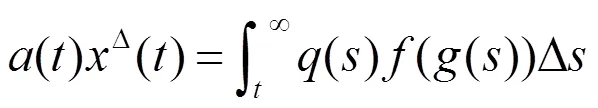
故有

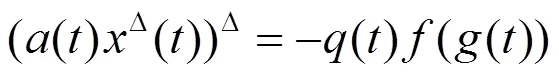
即得

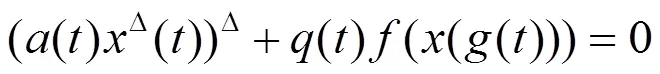
[1] Hilger S. Analysis on measure chains unified approach to continuous and discrete calculus[J]. Results in Mathematics,1990,18(1):18-56.

[2] Zhang B G, Zhu S. Oscillation of Second Order Nonlinear Dynamic Equations on Time Scales [J]. Computers Math Applic, 2005,49(4):599-609.

[3] Bohner M, Saker S H . Oscillation of Second-Order Nonlinear Dynamic Equations on Time Scales [J]. Rocky Mountain J Math, 2004,34(4):1239-1254.

[4] Erbe L, Peterson A, Saker S H. Oscillation Criteria for Second Order Nonlinear Dynamic Equations on Time Scales [J]. Math. Anal. Applic, 2007,333:505-522.

[5] 王志伟,邓志云,杨云苏.二阶非线性动力方程有界解振动的充分必要条件[J].井冈山大学学报:自然科学版，2013,34(5):9-12.

[6] Bohner M, Peterson A. Dynamic Equations on Time Scales[M]. Boston ：Birkhauser，2001.

SUFFICIENT CONDITIONS FOR SOLUTIONS OF SECOND ORDER DYNAMIC EQUATIONS ON TIME SCALES

*WANG Zhi-wei, DENG Zhi-yun, YANG Yun-su

(School of Mathematics and Physics, Jinggangshan University,Ji’an,Jiangxi 343009,China)

We mainly discuss the existence of the solution to a class of second order nonlinear dynamic equations on time scales. Firstly, we give two sufficient conditions for oscillation of solutions of second order nonlinear dynamic equations on time scales by the Riccati transformation and time scales theory. Secondly, a non-oscillation criterion that equation has bounded positive solutions was obtained by using the fixed point Theorem in Banach space.

second order dynamic equation; oscillation; time scales

O175.1

A

10.3969/j.issn.1674-8085.2014.06.003

1674-8085(2014)06-0015-04

2014-04-28；

2014-06-08

江西省教育厅教改课题项目(JXJG-12-15-11)

*王志伟(1977-)，男，江西吉水人，讲师，硕士，主要从事动力系统与稳定性的研究(E-mail:whzhwh_2003@126.com);

邓志云(1975-)，男，江西吉水人，副教授，硕士，主要从事应用数学的研究(E-mail:danzhiyun@163.com);

杨云苏(1968-)，女，江西泰和人，副教授，硕士，主要从事泛函分析研究(E-mail:pengyou19820124@163.com).