关于Karoubian范畴的推出范畴的一点注记

连冠勤，陈清华

关于Karoubian范畴的推出范畴的一点注记

*连冠勤1，陈清华2

(1.福建师范大学人民武装学院，福建，福州 350007；2. 福建师范大学数学与计算机科学学院，福建，福州 350007)

给定一个加法范畴，证明了如果是Karoubian范畴，则以中的推出为对象，推出态射为态射所构成的推出范畴0也是Karoubian范畴。

加法范畴；加法范畴的推出范畴；Karoubian范畴

1 预备知识

推出和拉回是范畴论中两个重要的对偶概念，因其丰富的性质而深受数学研究者的青睐。日本数学家Yoneda证明了利用推出与拉回定义的n-扩张与用投射与内射分解定义的n-扩张是同构的；Kosmatov N.V.于文[1]得到拉回环同调维数的上界; 文[2]中，唐、陈用逆极限刻画拉回的两种推广——集体拉回与I-拉回的关系；文[3-4]中给出了推出范畴的定义以及Abel范畴的推出范畴与平凡扩张的关系等等。这些都完善和发展了拉回和推出理论。Karoubian范畴(又称幂等完备的加法范畴)的性质十分接近Abel范畴，由文[5]知，任意的加法范畴的幂等完备化是Karoubian范畴，且幂等完备的三角范畴较一般的三角范畴具备更好的内在性质；文[6]研究三角范畴左recollement的幂等完备化；文[7]探讨了加法范畴推出范畴的幂等完备化与加法范畴的幂等完备化的推出范畴的关系。本文考虑Karoubian范畴的推出范畴。

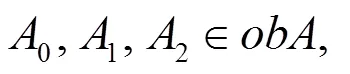
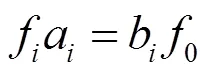
引理2[8]设是范畴，以中的推出为对象，推出态射为态射构成范畴，称之为的推出范畴，记为0。

引理3[8]加法范畴的推出范畴是加法范畴。

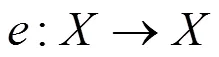
2 主要结论及证明

定理1 Karoubian范畴的推出范畴是Karoubian范畴。

证明 设是Karoubian范畴, 根据引理1.5得0是加法范畴。故只需证0中的任意幂等态射

[1] Kosmatov N V. Bounds for the homological dimensions of pullbacks[J]. Journal of Mathematical Sciences, 2002, 112(4):4367-4370.

[2] Chen Qinghua, Tang Lidan. Recollement, idempotent completion and t-structures of triangulated category[J]. J.Algebra, 2008, 319(7): 3053-3061.

[3] Balmer P, Schlichting M. Idempotent completion of triangulated categories[J]. J.Algebra, 2001, 236(2): 819-834.

[4] Osborne M S. Basic Homological Algebra[M]. New York: Springer-Verlag, 2000.

[5] 连冠勤. 加法范畴的推出范畴的幂等完备化[J]. 莆田学院学报, 2010(5):11-13.

[6] 贺伟. 范畴论[M]. 北京: 科学出版社, 2006.

[7] 唐丽丹, 陈清华. 广义拉回与推出[J]. 数学学报:中文版,2007, 50(4):759-774.

[8] 沈婧芳.推出范畴的性质[D].武汉:华中师范大学, 2006.

[9] 连冠勤, 陈清华. Abel范畴的推出范畴与平凡扩张[J]. 福建师范大学学报:自然科学版, 2012(2):1-3.

NOTE ON THE PUSHOUT CATEGORY OF KAROUBIAN CATEGORY

*LIAN Guan-qin1，CHEN Qing-hua2

(1. College of Military Studies, Fujian Normal University, Fuzhou, Fujian 350007, China；2. School of Mathematics and Computer Science, FujianNormal University, Fuzhou, Fujian 350007, China)

Letbe an additive category, we prove that ifis karoubian, so is its pushouts category0whose objects are the pushouts ofand whose morphisms are the pushout morphisms on.

additive category; the pushouts category of additive category; karoubian category

O154.1

A

10.3969/j.issn.1674-8085.2014.06.004

1674-8085(2014)06-0019-02

2014-04-15；

2014-06-08

国家自然科学基金项目(11071040）；福建省教育厅B类科技研究项目(JB12283)

*连冠勤(1984-)，女，福建莆田人，讲师，硕士，主要从事同调代数与代数表示论研究(E-mail: lgq0594@163.com);

陈清华(1962-)，男，福建莆田人，教授，博士，主要从事同调代数与代数表示论研究(E-mail:qhmath@fjnu.edu.cn).