变系数时间分数阶延迟微分方程的数值解法

刘明鼎，张艳敏

变系数时间分数阶延迟微分方程的数值解法

*刘明鼎，张艳敏

(青岛理工大学琴岛学院，山东，青岛 266106)

对一类变系数时间分数阶延迟微分方程给出了一种有限差分解法，将对时间的一阶导数利用(0＜＜1)阶导数来代替，同时证明了该格式的收敛性与稳定性，数值算例验证该方法有效。

变系数；时间分数阶；延迟微分方程；无条件收敛；无条件稳定

延迟微分方程模型在自然界中可以用来描述很多物理现象，而分数阶延迟微分方程是其中重要的一类方程，时间分数阶微分方程能更好的描述一些反常现象、多孔介质等问题的发生过程[1]。由于分数阶微分方程的解析解很难获得，所以很多学者为此研究数值解[1-5]。

本文将考虑如下初值时间变系数分数阶延迟微分方程：

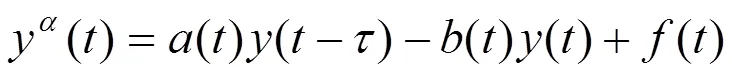
1 差分方程的构造

对式(4)化简得：

对方程(1)通过式(5)分情况写成如下两个差分方程：

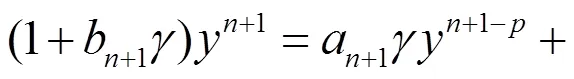
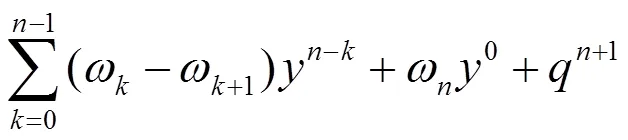
2 差分格式稳定性的证明

定理1 差分方程（6）、（7）是无条件稳定的。

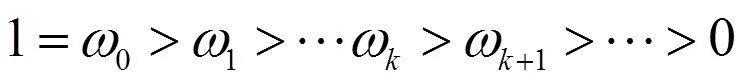
由式（6）、（7）得误差格式为：

则当=1时，由式(8)得：

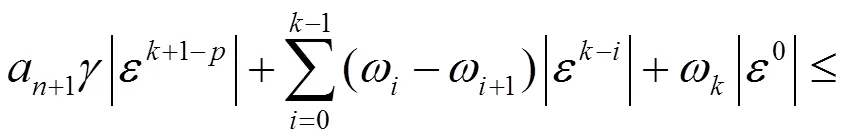
因此定理结论成立。

3 差分格式收敛性的证明

由局部截断误差定义以及式（3）、（6）、（7）得：

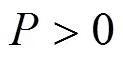
定理2 差分方程（6）、（7）是无条件收敛的。

证明：当=1时，由式(10)得：

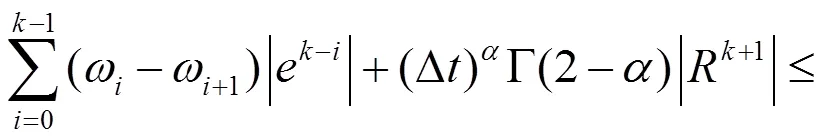
4 数值算例

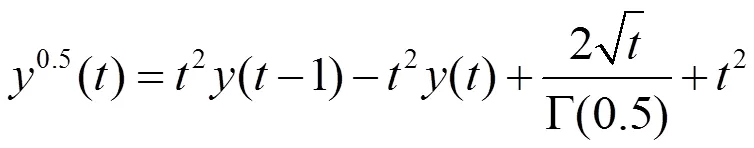
表1 数值解的相对误差

通过这个数值算例，可以说明本文给出的数值解法是解决此类问题的一个有效方法。

[1] 肖静宇. 几类分数阶微分方程的数值方法研究[D].哈尔滨:哈尔滨工业大学, 2013.

[2] 林玉闽. 时间分数阶偏微分方程的解及其应用[D].厦门:厦门大学,2008.

[3] 陈景华. 空间和时间分数阶偏微分方程[D].厦门:厦门大学,2007.

[4] 蔡新,刘发旺.解空间Riesz分数阶扩散方程的一种数值方法[J].高等学校计算数学学报,2005, 27(S1):242 -246.

[5] 马亮亮.变系数空间分数阶对流-扩散方程的有限差分解法[J].沈阳大学学报:自然科学版,2013,25(4): 341-344.

[6] Podlubny I. Frcational Differential Equations[M]. San Diego: Academic Press, 1999.

[7] 金承日,潘友思.时间分数阶色散方程的有限差分方法[J].黑龙江大学自然科学学报,2011,28(3): 291-294.

[8] 汤小松,刘清.一类分数阶微分方程积分三点边值问题的正解[J].井冈山大学学报:自然科学版,2013,31(1): 11-15.

NUMERICAL METHOD FOR SOLVING VARIABLE COEFFICIENTS TIME FRACTIONAL DELAY DIFFERENTIAL EQUATION

*LIU Ming-ding，ZHANG Yan-min

(Qindao College ,Qingdao Technological University, Qingdao, Shandong 266106, China)

A numerical method was given to solve a time fractional delay differential equation with variable coefficients, which the first order derivative was replaced by a fractional derivative of order(0＜＜1). Furthermore, we also prove the difference scheme is unconditional stable and unconditional convergence. Numerical example shows that the numerical method is a practical method.

variable coefficients; time fractional; delay differential equation; unconditional convergence; unconditional stable

O241.82

A

10.3969/j.issn.1674-8085.2014.06.001

1674-8085(2014)06-0001-03

2014-05-21；

2014-07-08

国家自然科学基金项目(11271101)

*刘明鼎(1982-)，男，辽宁大连人，讲师，硕士，主要从事偏微分方程数值解研究(E-mail:lmd0313@163.com);

张艳敏(1981-)，女，山东东营人，讲师，硕士，主要从事偏微分方程数值解研究(E-mail:elva810118@163.com).