求解无限长载流直螺线管磁场的两种方法比较＊

王小兰

（黄冈师范学院 湖北 黄冈 438000）

李春密

（北京师范大学物理系 北京 100875）

梁莉红

（萍乡市第六中学 江西 萍乡 337000）

恒定磁场是《普通物理学》里很重要的一部分学习内容.其中求解无限长载流直螺线管的磁场是个典型的问题.本文根据毕奥 －萨伐尔定律和安培环路定理两种方法来解析，并进行比较.

1 用毕奥 －萨伐尔定律求解

先讨论用毕奥 －萨伐尔定律求单匝圆形载流导线的磁场，然后根据磁场的叠加原理求多匝圆形载流导线的磁场.

【例1】设在真空中，有一半径为R圆形载流导线，通过的电流为I，通常称作圆电流.试求通过圆心并垂直于圆形导线平面的轴线电流上任意一点P处的磁感应强度.

解析：建立如图1所示的坐标系.其中Ox轴通过圆心O，并垂直圆形导线平面，在圆上任取一电流元Idl，这个电流元到场点P的位置矢量为r.根据毕奥 －萨伐尔定律在P点所产生的磁感应强度为

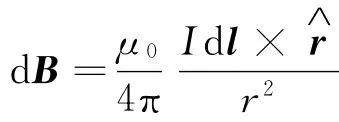
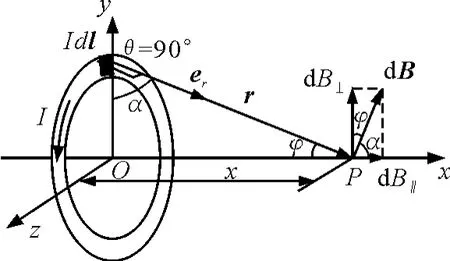
图1 圆形导线平面轴线电流上任一点的磁场

由图中受力分析可知，电流元Idl与位矢r垂直，所以θ＝90°，而dB的方向垂直于电流元Idl与位矢r所组成的平面，即dB与Ox轴的夹角为α.因此，我们可以把dB分解成两个分量：一是沿Ox轴的分量dBx＝dBcosα；另一是垂直于Ox轴的分量dB⊥＝dBsinα.

考虑到圆上任一直径两端的电流元对Ox的对称性，根据磁场叠加原理，所有电流元在点P处的磁感应强度的垂直分量dB⊥的总和应等于零；其在Ox轴上的分量dBx相互加强.所以

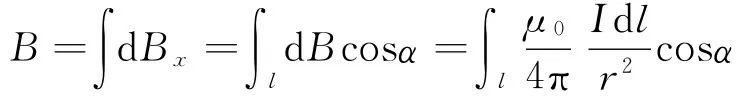
B的方向垂直于圆形导线平面，沿Ox轴正向.

讨论：

（1）当x＝0时，即圆心点O处的磁感应强度的量值为

其方向垂直于圆形导线平面，沿Ox轴的正方向.

（2）如果圆电流是由N 匝导线所组成的，通过每匝的电流强度均为I，则圆心点O处的磁感应强度的量值为

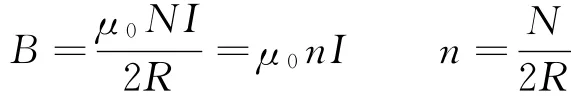
【例2】求长直载流螺线管的磁场1.

如图2所示，真空中有一长为l，半径为R的载流密绕直螺线管，总匝数为N（单位长度匝数为n）通有电流I.求管内轴线上一点处的磁感应强度B.

图2 通电螺线管

解析：无限长载流螺线管可看作是由多匝载流圆环构成.图3为螺线管的纵剖图.此剖面图设在纸面内.在距P点为x处取长为dx的一小段，dx上含有线圈ndx匝.因为螺线管上线圈绕得很密，所以，dx段相当于一个圆电流，电流强度为Indx.

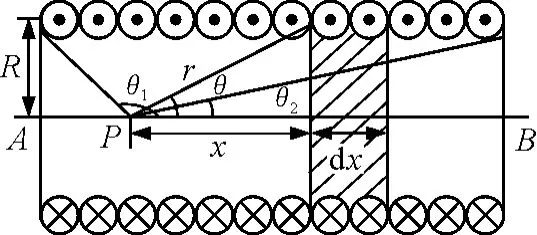
图3 求螺线管磁场

根据上题的结果和磁场叠加原理，它在P点产生的磁感应强度dB的大小为

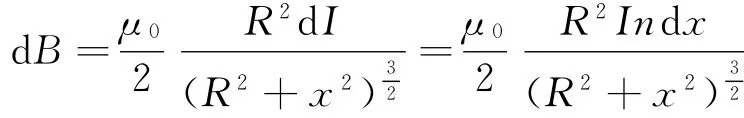
所有线圈在P点产生的dB均向右，所以P点B为

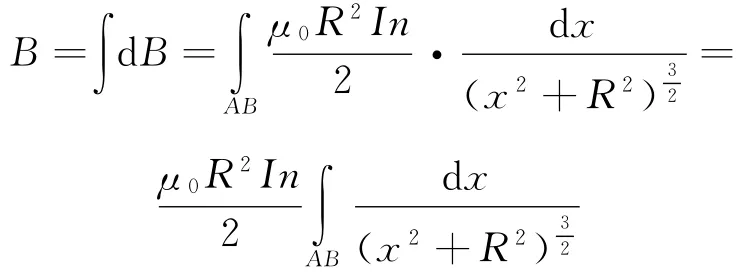
取点P到所取小段线圈的连线与轴线AB夹角θ为积分变量，由图可知

代入上式得

（1）讨论和推理几种特殊情况

1）如果螺线管为无限长，θ1＝π，θ2＝0，则

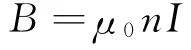
2）当点P处于管内轴线中点时，θ1＝π－θ2，cosθ1＝－cosθ2，而

代入计算结果得

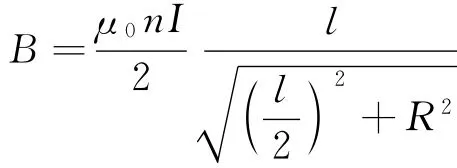
当lR时，细而长的螺线管可看作是无限长，由此得管内轴线中点处的磁感应强度为B＝μ0nI.

3）如果P点位于半无限长螺线管的一端，则

或者 θ1＝π θ2＝

代入上式得

这说明半“无限长”螺线管轴线上端点的磁感应强度只有管内轴线中点磁感应强度的一半.

4）我们可以根据实验数据不难画出图4，图中给出了长直螺线管内轴线上磁感应强度的分布.可以看出，密绕载流长直螺线管内轴线中部附近的磁场完全可视作均匀磁场，两端是非均匀磁场.

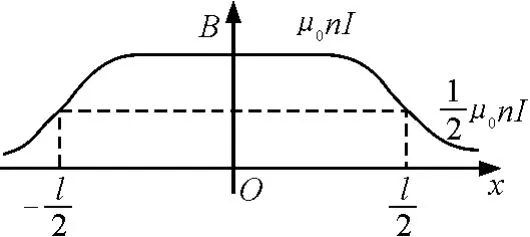
图4 通电螺线管内外磁场曲线

（2）推论：如果是无限长密绕载流直螺线管则内部是匀强磁场，数值大小与管轴上的磁感应强度B＝μ0nI相等，其方向轴平行.管外磁场很弱，可以忽略不计.

2 用安培环路定理求解

先根据安培环路定理求有磁介质的无限长载流直螺线管的磁场，再求真空中的无限长载流直螺线管的磁场.

【例3】设有螺线管长为l，共有N匝，电流为I，螺线管中磁介质的磁导率为μ.求无限长载流直螺线管的磁场.

解析：由于螺线管无限长，管内中央部分的磁场可以看作是匀强磁场，方向与螺线管的轴线平行.管的外侧磁场强度很弱，忽略不计.

为计算螺线管中段内部某点P的磁场强度可通过P点作一矩形闭合回路abcda（如图5所示），根据有磁介质的安培环路定理有

沿此闭合曲线求H矢量的线积分为

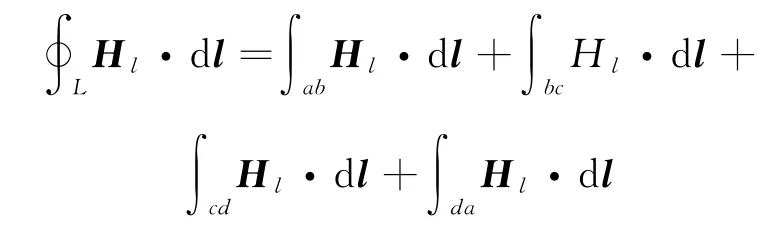
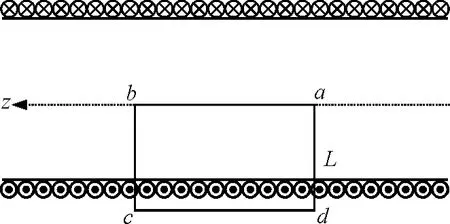
图5 求无限长载流直螺线管的磁场

在线段cd上，H＝0.在线段bc和da的管内部分上，虽然H ≠0，但dl与H 相互垂直，即

因此H矢量沿着闭合路径abcda线积分为

因为管内磁场是匀强的，方向自a向b，所以

所以螺线管内的磁场强度为

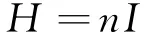
于是管内的磁感应强度为

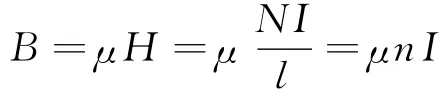
在真空中时

3 两种求解方法的比较

求解无限长载流直螺线管磁场的两种方法进行比较如表1所示［2］.

表1 两种方法比较

从上表可以看出：求解无限长载流直螺线管磁场的两种思路中，尽管所用方法如对称法、微分积分法、理想模型法、公式法、推理法等是相同的，但是运用安培环路定理的方法较为直接、简单、明了.运用安培环路定理解决本题，必须是建立无限长密绕载流直螺线管内部是匀强磁场，忽略了管外的磁场的认知基础上，第一种方法是第二种方法的铺垫，第二种方法是第一种方法的提升.无限长载流直螺线管磁场分布情况也是《普通物理学》中的一种理想的物理模型，通过两种方法的解析和比较，以期提高学生分析问题和综合解决问题的能力，促进学生元认知能力的发展.

1 马文蔚.物理学［上册］（第五版）.北京：高等教育出版社，2006.294～296

2 朱鈜雄.物理学方法概论.北京：清华大学出版社，2008.9～30