山区特殊地质条件下地基-箱基-上部结构地震响应分析

尚 军

(天津城建大学 a. 土木工程学院；b. 天津市软土特性与工程环境实验室，天津 300384)

我国属于多山地、多丘陵国家，即使平原地区也会存在少量坡地地形，随着城市建设用地日益减少，利用自然环境并与山地地形相适应的山地建筑越来越多.由于对地形的适应力强，对环境改造小，近年来山地建筑在城市中的应用越来越普遍，而且山地高层建筑也大量涌现[1].

目前山地建筑结构抗震设计可能存在安全隐患.在汶川地震震害调查中，发现若干典型山地结构房屋发生了倒塌的现象，暴露出设计中可能忽略或没有认识到的关键问题.山地建筑结构抗震设计理论体系研究严重滞后于工程实践的需要.为了保证山地建筑结构在具有良好抗震性能的前提下仍能达到不影响建筑功能及建筑美学的要求，真正做到建筑与结构的统一和协调，迫切需要进行山地建筑结构抗震分析与设计相关问题研究.那么，其相关研究将促进山地建筑的应用和发展，具有重要学术意义、理论价值和工程应用价值[2].

在我国，许多专家已经对山地建筑进行了大量研究.杨柏坡等[3-4]分析发现陡坎边沿、山顶地面运动的放大效应，研究了陡坎、陡峭山坡上方建筑房屋的地震反应差别.李山有等[5-6]对地震波斜入射情形下竖直、倾斜台阶地形引起的波形转换进行了数值模拟，发现地震波的斜入射会使台阶上角点引起更强的转换面波，转换面波振幅可达弹性半空间表面自由场位移的1.1倍左右.杨佑发等[7-9]建立了二维的土-结构相互作用ANSYS分析模型，并分析了多层接地建筑的抗震性能，发现结构的抗震性能受地基影响显著.王丽萍[10]分析了坡高及坡角变化对坡地斜坡段反应谱及谱比的影响规律，给出了岩质山地建筑结构设计水平地震动放大系数；同时还给出了需要考虑竖向地震动影响的山地工程结构设计竖向地震动的放大系数.

本文通过对 ABAQUS模型输入不同方向地震波，研究了岩质边坡地基-箱基-上部结构的位移响应，得出了一些有益的结论，为类似山地建筑的优化设计提供更多的理论支持.

1 工程概况

本文主要针对天津蓟县某山地住宅楼进行分析研究，该楼为6层框架结构，层高3 m，总高度21 m，长 69 m，宽 10 m.混凝土强度等级为 C30，板厚100 mm，梁截面尺寸 200 mm×400 mm，柱截面尺寸500 mm×500 mm.受蓟县当地地质条件的限制，建筑物建立在多台阶岩质边坡上，基础采用变高度箱型基础，基础混凝土强度等级为C40.上部结构、箱基础与边坡的地质构造如图1所示，岩质边坡岩层材料参数见表1.

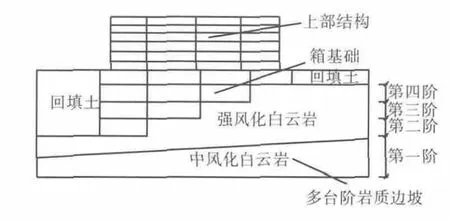
图1 上部结构、箱基础与岩质边坡地质构造

表1 岩质边坡土体材料参数

2 模型的建立及模态分析

2.1 模型的建立

采用大型通用有限元分析软件ABAQUS进行岩质边坡地基-箱基-上部结构三维整体建模和弹塑性有限元动力时程分析[11].结构计算时，重力荷载及地震加速度共同作用于模型上进行分析.为提高计算效率，取土体范围为 5倍的箱基尺寸进行有限元分析，5倍以外土体采用无限元模拟.因此，框架梁与柱均采用减缩积分实体单元C3D8R来模拟，使用减缩积分单元可以有效地避免剪切闭锁问题，并且单元形状对减缩积分单元的分析结果精度影响不大[12]；近场土体采用有限元方法模拟，也采用实体单元C3D8R模拟.远场土体采用无限元方法模拟，采用CIN3D8单元(8节点线性无限元)模拟，该单元的第一个面为有限元和无限元的交接面，在ABAQUS/Standard中，代表无限元伸展方向的节点与极点之间的距离应为交接点与极点之间距离的两倍.上部框架模型和整体模型如图2和图3所示.

图2 上部框架结构模型

图3 ABAQUS整体模型

2.2 模态分析

岩质边坡地基-箱基-上部结构中前三阶振型主要表现为上部结构的振型，箱基和地基的振动形态没有表现出来[13]，结果如图4和表2所示.

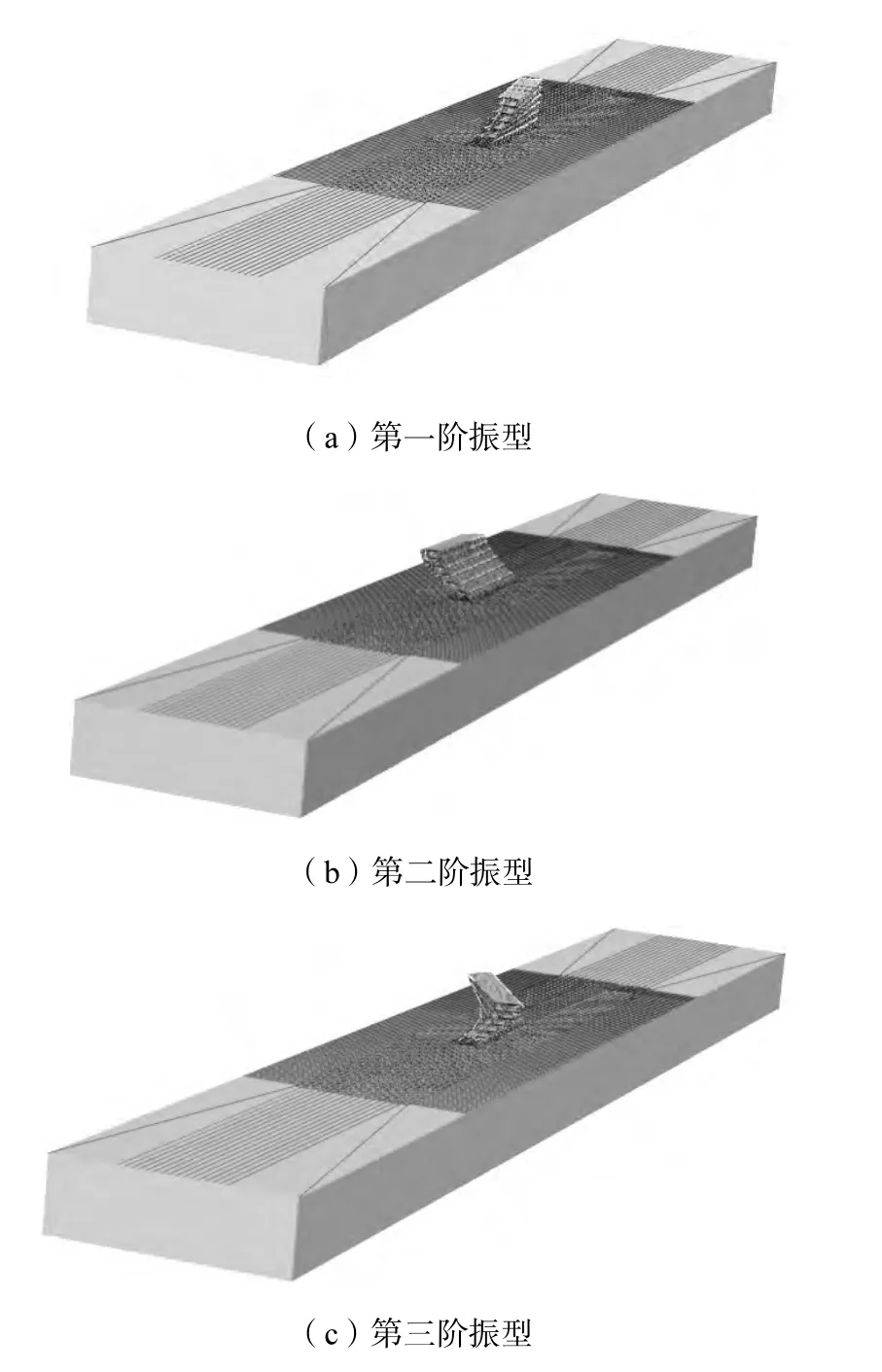
图4 岩质边坡地基-箱基-上部结构振型

表2 岩质边坡地基-箱基-上部结构振型特性

分析结果表明，体系前三阶振型均为上部结构的振动形态，由图4可以看出，第一、第二振型均为平动振型，第三振型为扭转振型.后续的高阶振型中出现了部分土体的局部振动，但在低阶振型中，主要以上部结构的振型为主.

2.3 地震波选取

本文选用天津宁河东西方向地震波和竖直方向地震波，Taft波水平方向地震波，人工波水平方向地震波.水平方向地震波施加方向为Z向，竖向地震波施加方向为Y向.两条波在基本设防烈度下的加速度时程曲线如图5所示.

图5 输入地震波加速度时程曲线

2.4 监测点的选取

本结构箱基础为非对称结构，且为台阶状，在地震作用下受力不对称，应选择具有代表性的断面，所以，选择垂直于短轴方向且经过中间柱的断面，在框架上设7个监测点KJ-A，KJ-B，KJ-C，KJ-D，KJ-E，KJ-F，KJ-G；箱基上设 4个断面 14个监测点，分别为断面1上XJ-1-A，XJ-1-B，XJ-1-C，XJ-1-D，XJ-1-E；断面2上XJ-2-A，XJ-2-B，XJ-2-C，XJ-2-D；断面3上XJ-3-A，XJ-3-B，XJ-3-C；断面4上XJ-4-A，XJ-4-B.其布置情况如图6所示.

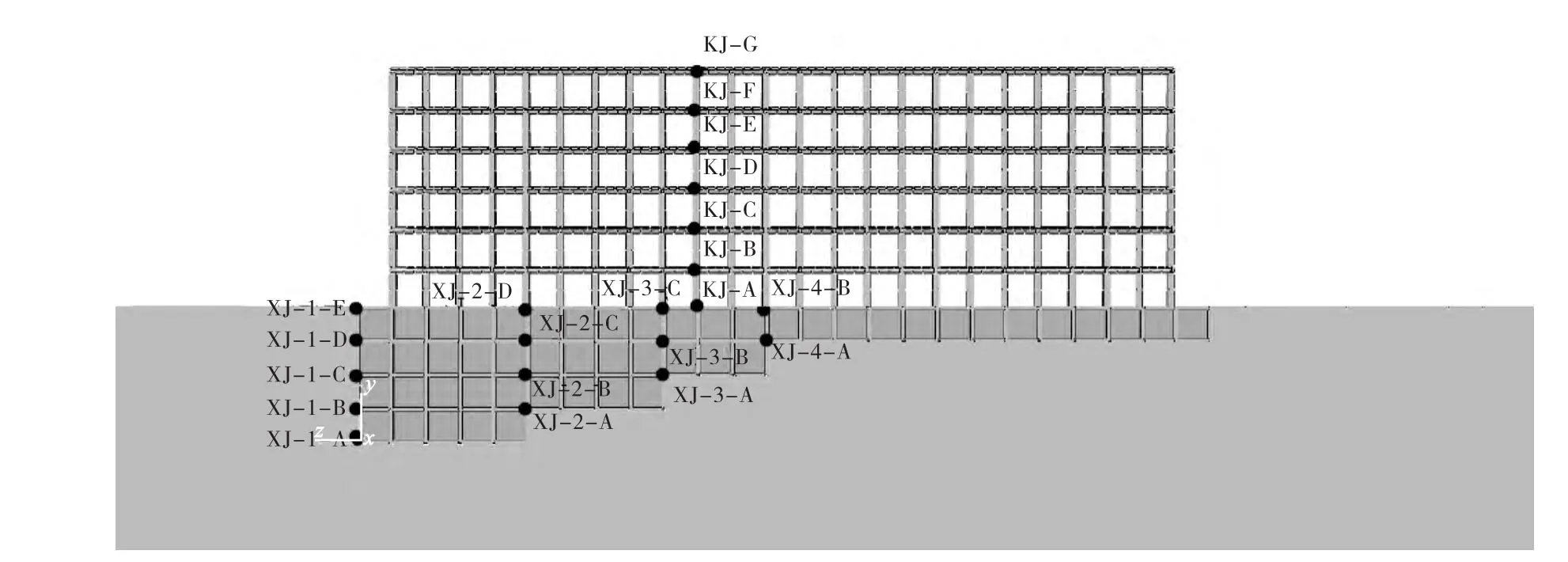
图6 结构关键监测点

3 地震作用下动力时程分析

水平地震作用一般被认为是结构遭到破坏的关键原因，故本节先对在基岩面输入的单向水平地震作用下的地下结构地震反应进行分析，输入的地震波为加速度峰值调至1.5 m/s2的东西向宁河天津波，对结构关键部位的位移变化规律进行了分析[14-15].

3.1 水平方向地震作用下位移反应分析

图7、图8分别给出了该结构体系在宁河天津地震波作用下，各关键点的位移响应情况.进一步分析，得出如表3、表4所示的各关键点的最大位移及最大位移出现的时刻.

分析该图表可知：在水平地震波的作用下，框架结构关键监测点最大绝对位移于13.22 s发生在顶层(关键监测点 KJ-G)，位移大小为 2.2211 cm，位移方向为Z轴正方向；随着层数降低最大位移值依次减小；反向最大绝对位移于11.89 s发生在顶层(关键监测点KJ-G)，位移大小为-1.0077 cm，位移方向为Z轴负方向；在地震波结束时产生永久位移，各层永久位移值大致相同，最大永久位移为1.1711 cm.

在水平地震波的作用下，台阶形箱基各关键点于15 s处发生最大绝对位移，最大绝对位移值为1.15 cm，位移方向为 Z轴正方向；反向最大绝对位移于6.69 s产生，最大绝对位移值为-0.354 cm，位移方向为Z轴负方向.

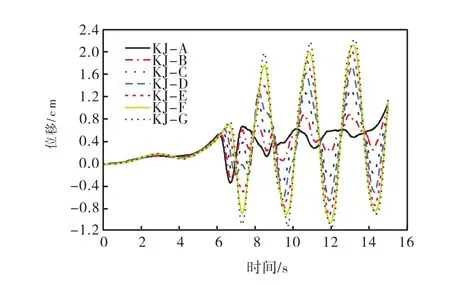
图7 框架关键监测点水平位移时程曲线

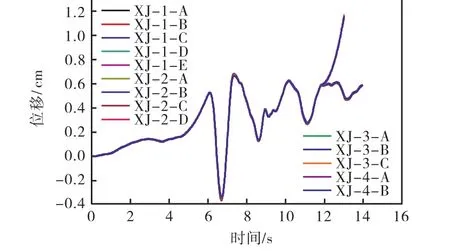
图8 箱基关键监测点水平位移时程曲线

表3 水平地震作用下框架每层绝对水平位移幅值

表4 水平地震作用下箱基每层绝对水平位移幅值

表 5给出了框架层间绝对位移最大值及峰值时刻.可看出，框架各层最大层间位移出现时刻有所不同，从一层开始层间水平位移幅值逐渐增大，在三层处最大层间位移幅值为最大，最大幅值为0.4114 cm，并且从三层开始向上最大层间位移幅值逐渐减小.

表6为水平地震作用下箱基各层间位移幅值.由表6可看出，箱基各层最大层间位移出现时刻相同，从负四层开始最大层间位移幅值逐渐增大，在负一层和负二层最大层间位移幅值为0.0013 cm，为各层最大值.

表5 水平地震作用下框架各层间位移幅值

表6 水平地震作用下箱基各层间位移幅值

3.2 竖直方向作用下位移反应分析

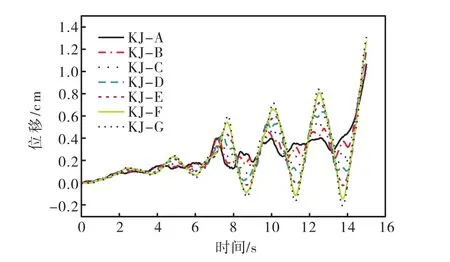
图9 框架关键监测点水平位移时程曲线

竖向地震作用下该结构体系的位移反应如图9-10所示，图中各关键点的选取与水平地震作用下相同.根据位移反应曲线图，进一步分析得出了竖向地震作用下各关键点的最大位移及峰值时刻，如表7-8所示.

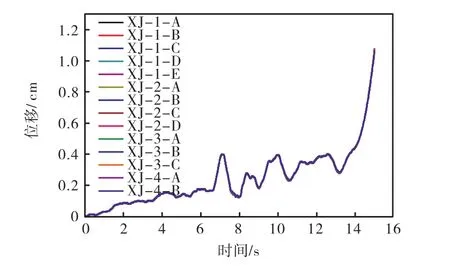
图10 箱基关键监测点水平位移时程曲线

表7 竖向地震作用下框架每层绝对水平位移幅值

表8 竖向地震作用下箱基每层绝对水平位移幅值

由图9和表7可得，在竖向地震波的作用下，框架结构关键点水平最大绝对位移于 15 s发生在顶层(关键监测点 KJ-G)，位移大小为 1.3103 cm，位移方向为Z轴正方向；随着层数降低各层水平最大位移值依次减小；反向最大绝对位移于13.74 s发生在顶层(关键点KJ-G)，位移大小为-0.2066 cm，位移方向为Z轴负方向；在地震波结束时产生永久位移，各层水平永久位移值各不相同，最大永久位移值出现在顶层(关键监测点KJ-G)，幅值为1.3103 cm.

在竖向地震波的作用下，台阶形箱基各关键点于15 s处发生水平最大绝对位移，最大绝对位移值为1.0791 cm，位移方向为Z轴正方向.

表9-10分别为竖向地震作用下框架和箱基各层间位移幅值.由表9可看出，在竖向地震作用下，框架各层水平最大层间位移幅值出现时刻全部相同，从二层开始最大层间位移幅值逐渐增大，在四层处达到最大，最大幅值为0.0925 cm，从四层开始逐渐减小.

由表10可看出，箱基各层最大层间位移出现时刻相同，在15 s处达到最大值，负四层最大层间位移幅值最大，方向为Z轴负方向，从负四层开始最大层间位移幅值逐渐减小，在负二层处达到最小层间位移幅值-0.0002 cm.

表9 竖向地震作用下框架各层间位移幅值

表10 竖向地震作用下箱基各层间位移幅值

3.3 竖直和水平方向耦合作用下位移反应分析

图11 框架关键监测点水平位移时程曲线

竖向地震及水平地震耦合作用下该结构体系的位移反应如图 11-12所示，各关键点的曲线变化步调基本一致.根据位移反应曲线图，进一步分析得出了耦合地震作用下各关键点的最大位移及峰值时刻，如表11-12所示.

图12 箱基关键监测点水平位移时程曲线

表11 水平和竖向地震共同作用下框架每层绝对水平位移幅值

表12 水平和竖向地震共同作用下箱基每层绝对水平位移幅值

由图11和表11可知，在水平和竖向地震波的耦合作用下，框架结构关键点最大绝对位移于 13.22 s发生在顶层(关键监测点 KJ-G)，位移大小为2.2235 cm，位移方向为Z轴正方向；随着层数降低最大位移值依次减小；最小绝对位移于 11.92 s发生在顶层(关键监测点 KJ-G)，位移大小为-0.9870 cm，位移方向为 Z轴正方向；在地震波结束时产生永久位移，各层永久位移值大致相同，顶层关键监测点产生最大永久位移，位移幅值为1.1140 cm.

由图12和表12可知，在水平和竖向地震波的耦合作用下，台阶形箱基各关键点于15 s处发生最大绝对位移，最大绝对位移值为1.0422 cm，位移方向为Z轴正方向，相对于水平地震波单独作用，最大绝对位移有所减小；反向最大绝对位移于6.69 s产生，最大绝对位移值为-0.3540 cm，位移方向为 Z轴负方向.

框架和箱基在水平和竖直双向地震耦合作用下，各关键点水平位移时程曲线与水平单向地震动作用下的关键点水平位移时程曲线规律大致一样，竖向地震单独作用下对水平位移的影响较大，而水平和竖向地震共同作用时竖向地震对水平位移影响较小，基本上与水平地震单独作用下的响应相同.

表 13-14是水平和竖向地震作用下框架和箱基各层间位移幅值.

表13 水平和竖向地震作用下框架各层间位移幅值

从表13可看出，在水平和竖向地震耦合作用下，最大层间位移变化规律均与水平单向地震作用下一致，从一层开始逐渐增大，三层达到最大层间位移幅值，三层以上逐渐减小，但是每层框架关键监测点绝对水平位移幅值不同，说明竖向地震的存在对框架最大层间位移有一定影响.

表14 水平和竖向地震作用下箱基各层间位移幅值

由表14可看出，在水平和竖向地震耦合作用下，箱基各层最大层间位移与单向水平地震作用下的各层层间位移相比，变化趋势刚好相反，从四层开始，最大层间位移由正方向向负方向变化，沿负方向逐渐增大，负一层达到反向最大，说明竖向地震波的存在对箱基层间位移的影响不可忽视.

4 结 论

通过输入不同方向的地震波，分析箱基和上部框架位移的变化规律，得出如下结论.

(1)框架和箱基在水平和竖直地震耦合作用下，各关键监测点水平位移时程曲线与水平单向地震动作用下的关键监测点水平位移时程曲线规律大致一样，竖向地震单独作用下对水平位移的影响较大，而水平和竖向地震耦合作用时竖向地震对水平位移影响较小，基本上与水平地震单独作用下的响应相同.

(2)在水平和竖向地震耦合作用下，箱基各层最大层间位移与单向水平地震作用下的各层层间位移相比，变化趋势刚好相反，从四层开始，最大层间位移由正方向向负方向变化，沿负方向逐渐增大，负一层达到反向最大，综上，说明竖向地震波的存在对箱基层间位移的影响不可忽视.

［1］吴 帅，谭 方. 山地建筑结构设计探讨[J]. 建筑结构，2013，43(11)：38-41.

［2］卢济威，王海松. 山地建筑设计[M]. 中国建筑工业出版社，2001.

［3］杨柏坡，杨笑梅. 复杂场地上结构地震反应的研究[J].地震工程与工程振动，1997，17(2)：10-15.

［4］杨柏坡，杨笑梅. 二维不均匀场地地震地面运动的估算[J]. 华南地震，1996，16(2)：1-9.

［5］李山有，廖振鹏. 地震体波斜入射情形下台阶地形引起的波型转换[J]. 地震工程与工程振动，2002，22(4)：9-15.

［6］李山有，金 星，陈 先，等. 地震动强度与地震烈度速报研究[J]. 地震工程与工程振动，2002，22(6)：1-7.

［7］杨佑发，王一功，李元初. 山区台地框架建筑抗震性能研究[J]. 振动与冲击，2007，26(6)：36-51.

［8］王一功，杨佑发. 多层接地框架土-结构共同作用分析[J]. 世界地震工程，2005，25(3)：88-93.

［9］杨佑发，王一功. 倾斜基岩上的土-框架相互作用研究[J]. 地震工程与工程振动，2005，25(2)：177-182.

［10］王丽萍. 山地建筑结构设计地震动输入与侧向刚度控制方法[D]. 重庆：重庆大学. 2010.

［11］尚守平，鲁华伟，邹新平，等. 土-结构动力相互作用结构自振周期的研究[J]. 地震工程与工程振动，2013，33(4)：117-125.

［12］王玉镯，傅传国. ABAQUS结构工程分析及实例详解[M]. 北京：中国建筑工业出版社，2010.

［13］张 曼，曾长女. 田文礼. 粉土地区上部结构与地基基础共同作用有限元分析[J]. 岩土工程学报，2013，33(7)：462-467.

［14］伍 平，于建华. 结构抗震设计中地震动输入的若干问题[J]. 西南交通大学学报，2012，37(11)：44-49.

［15］夏栋舟，何益斌，刘建华. 刚性桩复合地基-上部结构动力相互作用体系抗震性能及影响因素分析[J]. 岩土力学，2009，30(11)：3505-3511.