基于多核环境的并行性双向枚举连接

陈永恒，左祥麟

（吉林大学 计算机科学与技术学院，长春130012）

多核处理器先将多个完全功能的核心集成在同一芯片内，再将整个芯片作为统一的结构对外提供服务［1－2］.多核处理器先通过集成多个单线程处理核心或集成多个同时多线程处理核心，使整个处理器可同时执行的线程是单处理器的数倍，极大提升了处理器的并行性能［3－5］.

通过利用多核处理器框架，文献［6］首次提出了并行查询优化PDPsva算法，该算法主要是将连接对的生成和查询计划的生成进行分离，并为了避免查询计划生成过程中访问连接对产生的冲突，依据连接对中关系的数量进行分组，从而将所有连接对转换成偏序对，最后根据组间依赖和组内并行的特点，实现部分查询计划自底向上的多线程并行构建.因而PDPsva算法是以连接对中包含连接表的数目为驱动产生最优查询计划.而动态规划算法DPccp［7］和DPhyp［8］通过直接遍历查询图生成连接对，进一步优化解决了PDPsva算法中枚举算法带来的无效连接对问题.本文提出一种DPbid算法，该算法通过结合上述两种方法的优点，实现了最优查询计划的并行化生成.

1 DPbid算法

基于自底向上动态规划算法会产生大量不可连接的匹配连接对，而自顶向下枚举算法的逻辑转换是依据逻辑转换规则随机产生的，且每次都需使用查询图特性控制笛卡尔积的产生.针对两种遍历方式的优缺点，本文提出一种DPbid算法.

1.1 算法框架

DPbid算法包括如下3步：

1）通过图遍历构建公共表，该公共表对连接匹配的每个连接对进行编码，从而提高了由上至下遍历时的逻辑转换效率，避免了成本较大的笛卡尔积运算；

2）采用自底向上动态规划算法并行求解包含少于或等于两个表部分解的最优计划；

3）基于连接对及步骤2）中产生的部分最优解，执行自顶向下的动态规划算法.

DPbid算法流程如下：

DPbid算法通过生成单表的最优查询计划初始化全局解Memo，将连接对的生成和查询计划的生成进行分离，Partition算法利用图遍历生成连接对，并对其进行编码.使用Reorder对生成的连接对分组，从而将所有连接对转换成偏序对.最后根据组间依赖和组内并行的特点，DownUpQEPs实现部分查询计划自底向上的多线程并行构建.根据不同的访问路径和连接方法，DownUpQEPs递归的从Group中访问每个连接对.对于生成的部分解QEP1和QEP2，如果QEP2的成本小于QEP1的成本，则PrunePlans剪枝掉QEP1，并利用全局变量Memo保存生成的最优查询计划.

1.2 Partition分割

在自底向上和由上至下枚举过程中，连接对的生成非常重要.Partition算法能产生避免笛卡尔积运算的连接对.

Partition算法流程如下：

CmpSub算法流程如下：

MinOptimistic算法流程如下：

所有连接的子图都可以通过Partition算法实现.Partition算法先将每个节点入队，对于队列中每个节点｛v｝，通过调用MinOptimistic扩展该节点，从而取得更大的连接子图，然后通过调用CmpSub获得子图的互补子图.MinOptimistic是自调用递归函数，主要通过调用邻接函数扩展节点，返回所有的连接子图.若s是无向图G的一个连接子图，s′是N（s）的子集，则s∪s′是可连接的.MinOptimistic基于该理论为线索构造所有的连接子图.CmpSub针对每个调用MinOptimistic产生连接子图及互补连接子图.

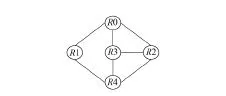
图1 查询图GFig.1 Query graph G

例如，对如图1所示的查询图G，利用partition和reorder函数，可得到图2中的一个表.图2包含了所有通过调用partition得到的连接对.这些连接对依据其包含连接表的多少进行分组和编码.

图2 连接对结构及编码Fig.2 Join－pair structure and coding

1.3 自顶向下枚举TopDownEnum

TopDownEnum算法先检测全局变量Memo，对于分解出的物理表达式G，如果其成本小于上限且Memo中存在其最优查询计划，则返回最优查询计划；否则，如果Memo中不存在其最优解，则调用Commutativity.Commutativity利用构建的连接对组Group实现逻辑表达式的进一步等价逻辑分解变换.TopDownEnum算法中的MatchSearch用于实现这种逻辑分解变换.例如，对于图2中Group［4］的R0R1R2，可利用遍历Group［3］中LVA∪RVA为｛0，1，2｝的所有连接对 QS实现其逻辑变换.

TopDownEnum算法流程如下：

Commutativity算法流程如下：

2 性能分析

下面将DPbid算法与使用LBUsize表示的自底向上动态规划PDPsva算法［6］及使用LDPbid表示的自顶向下动态规划算法进行比较.表1列出了用于实验测试的3种算法.查询类型分别针对chain，cycle，star和clique查询图，图3～图6为不同算法的相对时间.由于不同的查询规模其优化时间也不同，所以不同算法的性能比较都是以LDPbid为基准进行的，LDPbid的优化时间是常数5.实验运行于Windows Vista系统，且具有两个Intel Xeon Quad Core E540 1.6GHz CPUs，8Gb物理内存，每个CPU具有4Mb L2缓存.

表1 运行算法Table 1 Run algorithms

针对chain查询，图3比较了LDPbid，LCTD和LBUsize算法的相对性能.由图3可见，LDPbid算法总是优于LCTD算法和LBUsize算法.而随着查询规模的增大，LBUsize算法会产生大量的笛卡尔积连接对，因而LBUsize算法性能下降最快.图4～图6的运行结果与此类似.由于LDPbid算法产生的枚举连接对明显少于LCDT算法和LBUsize算法，因而其空间复杂度也明显降低.

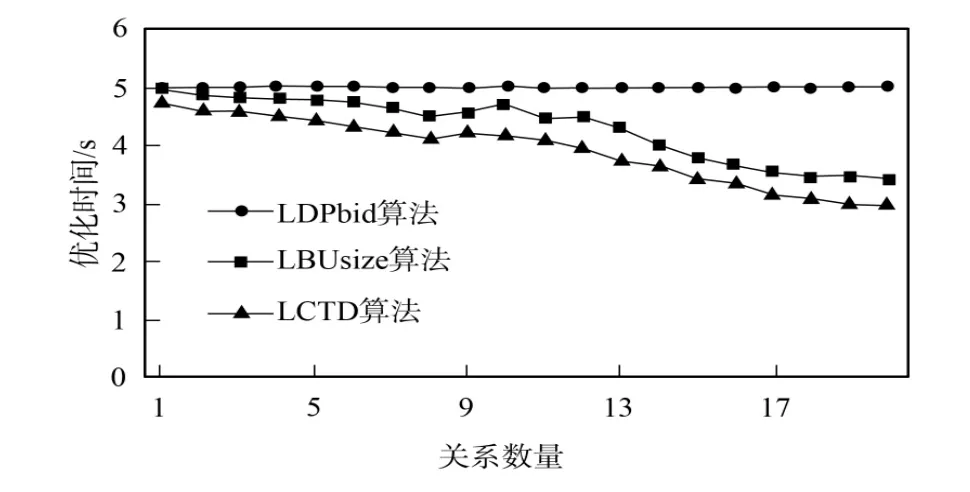
图3 Chain查询时3种算法的相对性能Fig.3 Relative performance of 3 algorithms for chain query

图4 Star查询时3种算法的相对性能Fig.4 Relative performance of 3 algorithms for star query

综上所述，本文提出了双向连接枚举并行算法，该算法结合了传统自底向上和自顶向下动态规划算法的优点，利用图遍历得到的连接对公共表，采用双向连接枚举的并行算法，充分发挥多核环境的优势，优化了传统自顶向下的动态规划算法中的逻辑转换性能.实验结果表明，该算法在时间和空间性能上都优于传统算法.

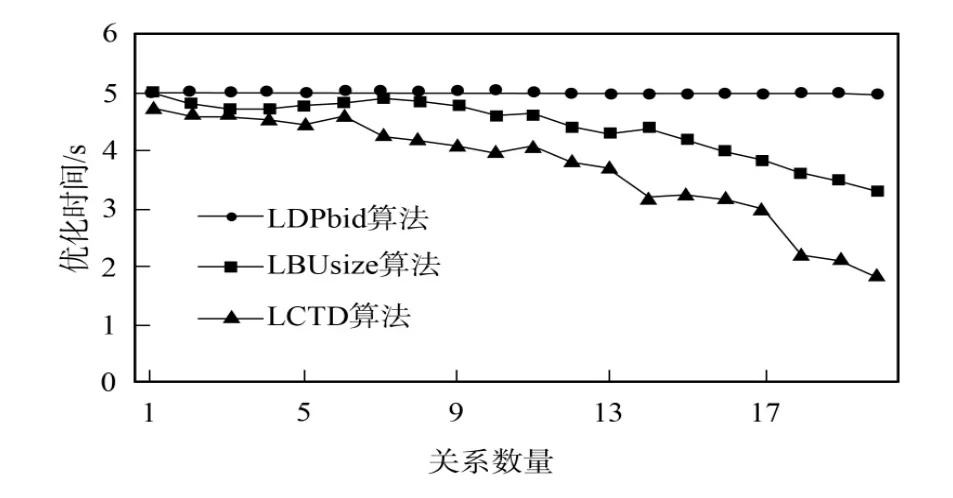
图5 Cycle查询时3种算法的相对性能Fig.5 Relative performance of 3 algorithms for cycle query

图6 Clique查询时3种算法的相对性能Fig.6 Relative performance of 3 algorithms for clique query

［1］Banikazemi M，Poff D，Abali B.Pam：A Novel Performance／Power Aware Meta－Scheduler for Multi－core Systems［C］／／Proccedings of the 2008ACM／IEEE Conference on Supercomputing.Piscaraway：IEEE Press，2008：24－36.

［2］Sutter H，Larus J.Software and the Concurrency Revolution ［J］.Queue：Multiprocessors Que，2005，3（7）：54－62.

［3］ZHOU Jing－ren，Cieslewicz J，Ross K A，et al.Improving Database Performance on Simultaneous Multithreading Processors［C］／／Proccedings of the 31st International Conference on Very Large Data Bases.New York：ACM Press，2005：49－60.

［4］Stenström P.Ipdps Panel：Is the Multi－core Roadmap Going to Live up to Its Promises［C］／／IEEE International Conference on Parallel and Distributed Processing Symposium.Piscaraway：IEEE Press，2007：14－15.

［5］Ailamaki A，Dewitt D J，Hill M D，et al.DBMSs on a Modern Processor：Where Does Time Go ［C］／／Proccedings of the 25th International Conference on Very Large Data Bases.New York：ACM Press，1999：266－277.

［6］Han Wook－Shin，Lee J.Dependency－Aware Reordering for Parallelizing Query Optimization in Multi－core CPUs［C］／／Proccedings of the 2009ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2009：45－58.

［7］Guido M，Thomas N.Analysis of Two Existing and One New Dynamic Programming Algorithm for the Generation of Optimal Bushy Join Trees without Cross Products ［C］／／Proceedings of the 32nd International Conference on Very Large Data Bases.New York：ACM Press，2006：930－941.

［8］Moerkotte G，Neumann T.Dynamic Programming Strikes Back ［C］／／Proceedings of the 2008ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2008：539－552.