线性模型参数一类新的s－K估计

吴 燕，何道江

（安徽师范大学 统计系，安徽 芜湖241003）

0 引 言

考虑线性回归模型：

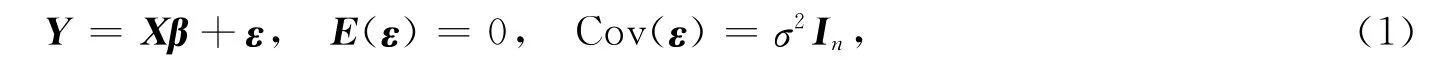
其中：Y为n维可观测随机向量；X为n×p阶设计矩阵，且rank（X）＝p；β为p×1维参数向量；ε为n维随机误差向量；σ2＞0是未知参数.

对于模型（1），β的最小二乘估计（LSE）为

LSE是无偏估计，其在很长一段时间内被认为是最好的估计.但当模型出现复共线性时，LSE的表现较差，有较大的均方误差.为了克服这一缺点，研究者们放弃了无偏性，提出了一些有偏估计.如Hoerl等［1］提出了岭估计（RE）：

其中k＞0是可选参数，称为岭参数.岭估计的本质是在设计阵的计算中引入一个偏参数k，通过合理取k值减少由复共线性带来的误差.之后，Hoerl等［2］又提出了岭估计的一种推广形式，称为广义岭估计（GRE）：

其中：K＝diag（k1，k2，…，kp），ki＞0（i＝1，2，…，p）为参数；Q＝（φ1，φ2，…，φp）为标准正交阵，而φ1，φ2，…，φp为X′X 的标准正交化特征向量，即Q′X′XQ＝diag（λ1，λ2，…，λp），λ1≥λ2≥…≥λp＞0为X′X的特征值.岭估计和广义岭估计都是岭参数的一个复杂函数，因此如何选择合理的岭参数是一个困难问题.

文献［3］提出了一种均匀压缩估计即Stein估计，表示为

其中s＞1称为压缩参数.Stein估计是最简单的一种有偏估计.

Swindel［4］基于参数向量β的先验信息，提出了改进的岭估计（MRE）：

其中：η0是一个给定的非随机向量，其选择依赖于β的先验信息；k＞0是岭参数.

许莹等［5］针对混合系数线性模型提出了一类新估计，称为s－K 估计.对于模型（1），相应的估计为

其中：K＝diag（k1，k2，…，kp），ki≥0（i＝1，2，…，p）为可选参数；s≥1为压缩参数.

本文在文献［4－5］的基础上，基于参数向量β的先验信息提出一类新的s－K 估计，称为改进s－K 估计.

1 改进s－K估计的定义

若令

定义1 对于模型（1），β改进s－K 估计定义为

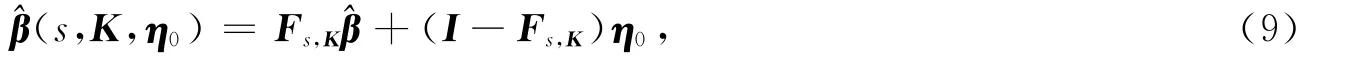
其中：s和K意义同式（7）；η0是β的先验信息.

注1 改进s－K 估计实际上是最小二乘估计与先验信息η0的一个“凸组合”.

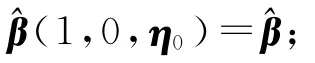
记Z＝XQ，α＝Q′β，则模型（1）可改写成：

其中Z′Z ＝Q′X′XQ ＝Λ∶＝diag（λ1，λ2，…，λp）.模型（11）称为模型（1）的典则形式.

对于典则形式（11），α相应的估计为

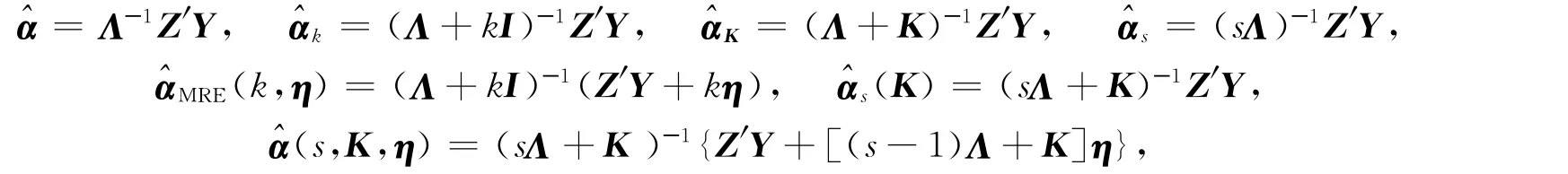
这里η＝Q′η0.

由于

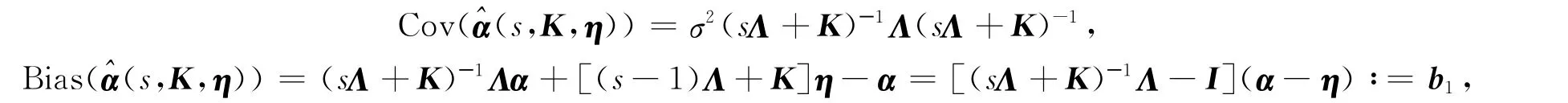
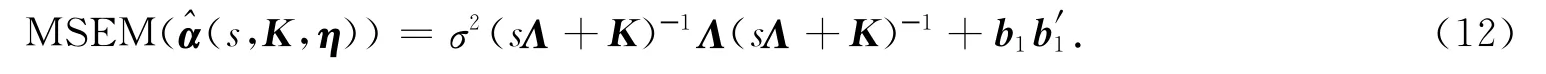
2 改进s－K估计的优良性

下面在均方误差阵的准则下，研究改进s－K 估计相对于最小二乘估计、广义岭估计、Stein估计、改进的岭估计及s－K 估计的优良性.

引理2［7］设M 为p阶正定阵，γ是p维列向量，则M－γγ′＞0当且仅当γ′M－1γ＜1.

2.1 改进s－K估计相对于最小二乘估计的优良性

2.2 改进s－K估计相对于广义岭估计的优良性

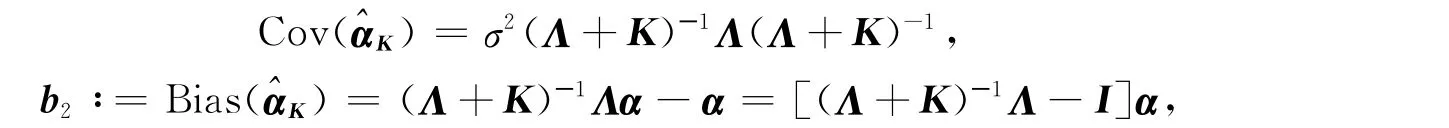
于是

从而

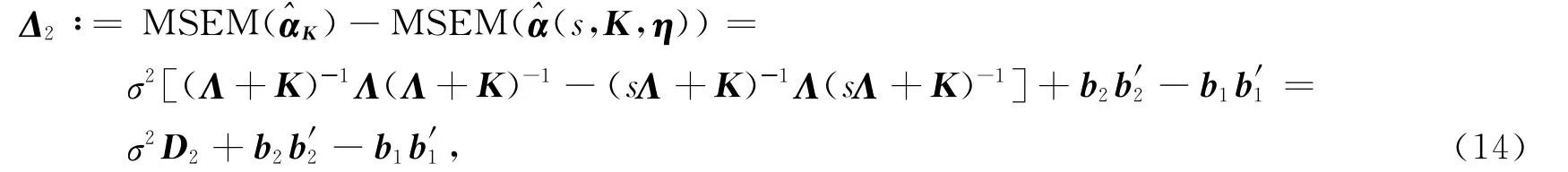
进而可得：

定理2 设s＞1，则改进s－K 估计的均方误差阵小于广义岭估计均方误差阵的充要条件是b′1（σ2D2＋b2b′2）－1b1＜1.

2.3 改进s－K估计相对于Stein估计的优良性

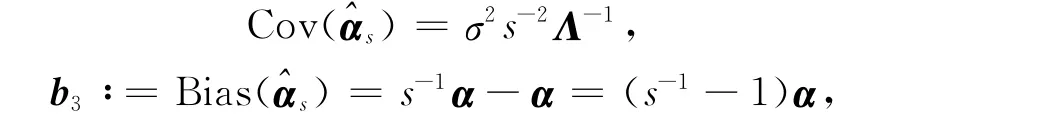
定理3 设ki＞0（i＝1，2，…，p），则改进s－K 估计的均方误差阵小于Stein估计均方误差阵的充要条件是b′1［σ2D3＋b3b′3］－1b1＜1.

2.4 改进s－K估计相对于改进岭估计的优良性

于是

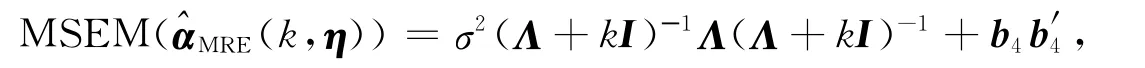
从而

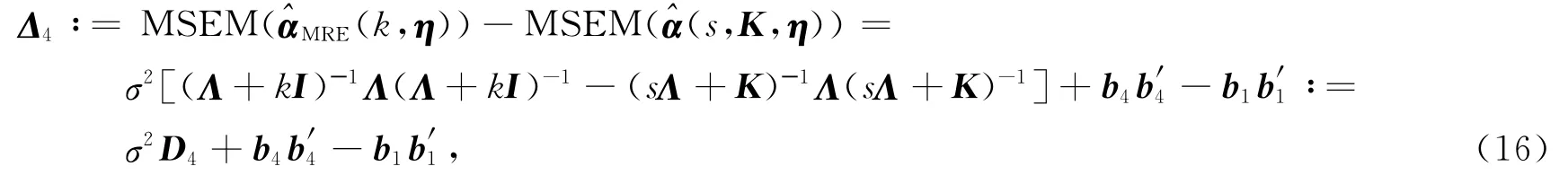
定理4 设ki＞（1－s）λi＋k（i＝1，2，…，p），则改进s－K 估计的均方误差阵小于改进岭估计均方误差阵的充要条件是b′1［σ2D4＋b4b′4］－1b1＜1.

2.5 改进s－K估计相对于s－K估计的优良性

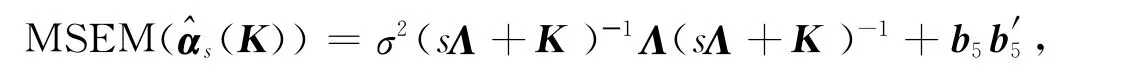
从而

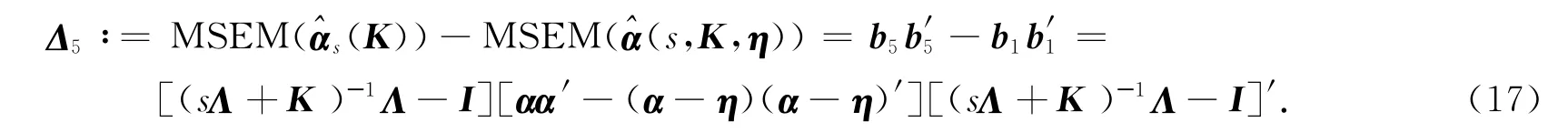
由此可得：

定理5 设s＞1，则改进s－K 估计的均方误差阵小于s－K 估计均方误差阵的充要条件是αα′－（α－η）（α－η）′＞0.

3 数值模拟

为进一步考察所提估计类的均方误差，下面进行Monte Carlo数值模拟.模拟中，设计矩阵X＝（xij）n×p和响应变量y＝（y1，y2，…，yn）′分别由下式给出：

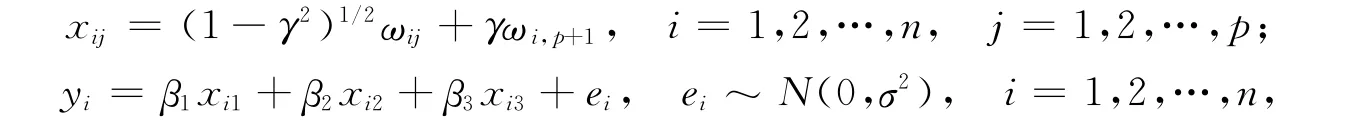
其中：ωij（i＝1，2，…，n；j＝1，2，…，p＋1）由独立的标准正态随机数产生；γ为给定的数，γ越大，表明解释变量间的相关性越强，从而模型的复共线性越强.取σ＝1，p＝3，n＝100，β的真实值取为X′X最小特征值所对应的特征向量［8］.与文献［9］相同，取先验信息η＝0.95β.实验的重复次数为N＝10 000，对于β＝（β1，β2，β3）′的估计，均方误差按下式计算：

最小二乘估计（LSE）、岭估计（RE）、Stein估计（Stein）、改进的岭估计（MRE）、s－K 估计（s－K）以及本文提出的改进s－K估计的均方误差数值模拟结果分别列于表1～表6.它们分别对应于σ＝1，2及γ＝0.9，0.99，0.999的6种情况.

对应于γ＝0.9，0.99，0.999，X′X 的条件数Cond（X′X）分别为9.868 7，93.785 5，941.244 6.根据文献［6］知，若Cond（X′X）＜100，则复共线性很小；若100＜Cond（X′X）＜1 000，则存在中等程度的复共线性；若Cond（X′X）＞1 000，则存在严重的复共线性.可见，模拟中设定模型的复共线性不很严重.

表1 σ＝1，γ＝0.9时各估计的均方误差Table 1 Simulated MSEs of estimators whenσ＝1，γ＝0.9

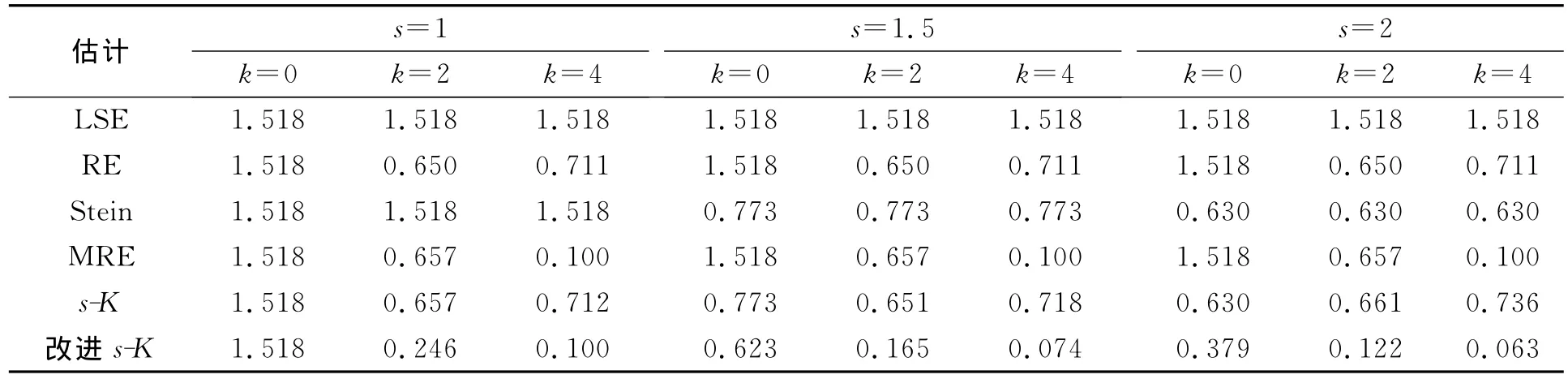
表2 σ＝1，γ＝0.99时各估计的均方误差Table 2 Simulated MSEs of estimators whenσ＝1，γ＝0.99

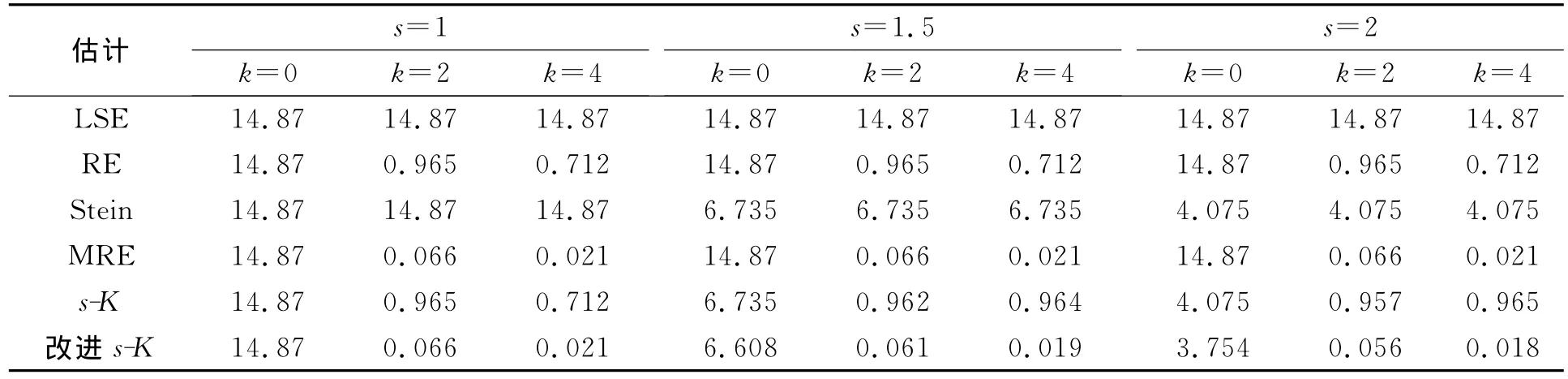
表3 σ＝1，γ＝0.999时各估计的均方误差Table 3 Simulated MSEs of estimators whenσ＝1，γ＝0.999

表4 σ＝2，γ＝0.9时各估计的均方误差Table 4 Simulated MSEs of estimators whenσ＝2，γ＝0.9

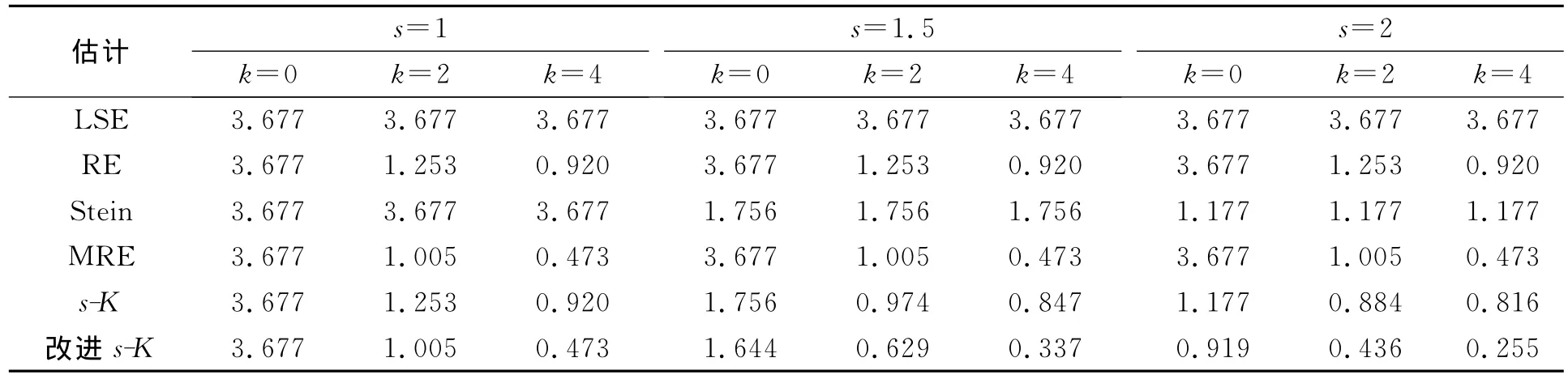
表5 σ＝2，γ＝0.99时各估计的均方误差Table 5 Simulated MSEs of estimators whenσ＝2，γ＝0.99

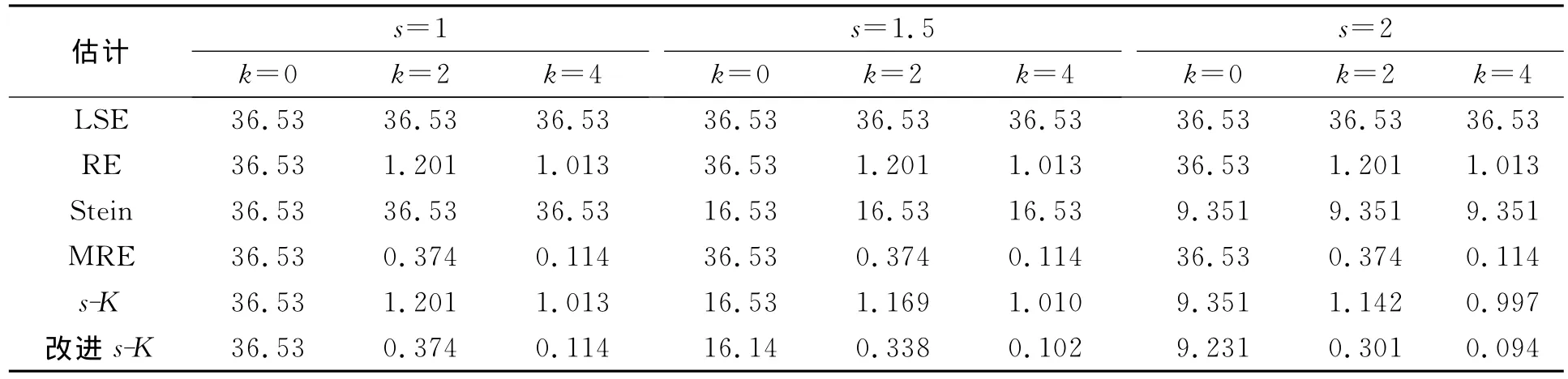
表6 σ＝2，γ＝0.999时各估计的均方误差Table 6 Simulated MSEs of estimators whenσ＝2，γ＝0.999

由表1～表6可见，改进s－K估计性能最好，除s＝1或K＝0的平凡场合外，其均方误差都小于最小二乘估计、岭估计、Stein估计、改进的岭估计以及s－K估计.

［1］Hoerl A E，Kennard R W.Ridge Regression：Biased Estimation for Nonorthogonal Problems ［J］.Technometrics，1970，12（1）：55－67.

［2］Hoerl A E，Kennard R W.Ridge Regression：Application to Nonorthogonal Problems［J］.Technometrics，1970，12（1）：69－82.

［3］Stein C.Inadmissibility of the Usual Estimator for Mean of Multivariate Normal Distribution ［C］／／Proc Third Berkeley Symp Math Statist Probab.Oakland：University of Calif Press，1956：197－206.

［4］Swindel B F.Good Ridge Estimators Based on Prior Information［J］.Communications in Statistics：Theory and Methods，1976，5（11）：1065－1075.

［5］XU Ying，HE Dao－jiang.A New Class of Estimators for Coefficients in Mixed Effect Linear Model［J］.Acta Mathematica Scientia，2013，33A（4）：702－708.（许莹，何道江.混合系数线性模型参数的一类新估计 ［J］.数学物理学报，2013，33A（4）：702－708.）

［6］王松桂，史建红，尹素菊，等.线性模型引论 ［M］.北京：科学出版社，2004.

［7］Farebrother R W.Further Results on the Mean Square Error of Ridge Regression［J］.J R Stat Soc B，1976，38（3）：248－250.

［8］LIU Ke－jian.Using Liu－Type Estimator to Combat Collinearity［J］.Communications in Statistics：Theory and Methods，2003，32（5）：1009－1020.

［9］LI Ya－lian，YANG Hu.A New Liu－Type Estimator in Lingear Regression Model［J］.Statistical Papers，2012，53（2）：427－437.