基于储存策略的仓库容量需求研究

邓正华

（重庆第二师范学院 经济与工商管理系，重庆 400067）

1 引言

无论是生产企业还是商业企业，一般都存在大量的产品库存，此时，仓库容量的选择是一个重要的决策问题，也是仓库设计、建造时需要分析的一个重要内容。然而，目前仓储管理的大量研究都是基于给定仓库容量进行优化研究。比如，肖建和郑力（2008）在给定仓库容量的情况下，根据物料相关性及用料频率，建立了检修备品库货位分配的多目标优化数学模型[1]。陈璐和陆志强（2012）利用混合整数规划方法，建立了储位分配和存取作业路径同时决策时的优化模型，并提出了两阶段算法进行求解[2]。戴韬和郑欣（2012）在给定仓库容量的情况下，建立了基于分类随机存储策略最小拣货时间的货位优化模型及求解算法[3]。

与上述文献不同，本文将仓库容量作为研究对象，试图构建不同储存策略下的仓库容量需求模型。Tompkins（2010）指出，在确定仓储作业的空间需求时，要考虑库存水平、存储单位、存储方法和策略等因素[4]。在同样的产品储存需求情况下，不同储存策略需要的仓库容量并不相同。如果在仓库容量需求估计时，没有考虑储存策略的影响，则仓库运行过程中就很有可能出现仓库容量与储存需求不匹配等问题。

因此，本文将基于储存策略研究仓库容量需求问题，构建不同储存策略下仓库容量需求的一般模型。

2 基本模型描述

假设某企业仓库准备储存n种产品，计算仓库容量需求时，显然未来每种产品的储存量并不确定，只能根据历史数据和经验来确定其储存量的分布。假设第i种产品的储存量为Yi，所有产品的储存量Y服从多元正态分布，即Y=(Y1,Y2,…,Yn)T～Nn(μ,Σ)，其中：

说明：本文中产品储存量都是指转换为标准储存单元后的储存数量，而不是直接指代产品个体的数量。

3 不同储存策略下仓库容量需求模型

3.1 定位储存策略

定位储存策略是指为每种产品事前分配一个固定的储存位置和空间，每种产品只能存放于自己的储存空间内，不同种类产品储存位置不能共用[5]。

假设企业要求定位储存策略下第i种产品的仓库容量保证率为βdi，i=1,2...,n。令定位储存策略下第i种产品分配的储存容量为 Xdi，则由 P(Yi≤Xdi)=βdi得：

其中，αdi为定位储存策略下第i种产品仓库容量的安全系数，等于 βdi对应的标准正态分布分位数；δii表示第i种产品储存量的方差。

因此，定位储存策略下整个仓库的储存容量需求为：

3.2 随机储存策略

随机储存策略是指事先不为每种产品分配固定的储存空间，在产品入库时，可以根据需要将其放在任何可以存放的空位上。因此，该策略下整个仓库的储存容量需求与未来的储存总量相关。令仓库未来的储存总量，由正态分布的性质知[6]，

假设随机储存策略下要求整个仓库容量的保证率为βs。令该策略下整个仓库储存容量需求为Xs，则由P(Ys≤Xs)=βs得：

其中，αs为随机储存策略下整个仓库容量的安全系数，等于βs对应的标准正态分布分位数。

3.3 分类随机储存策略

假设分类随机储存策略下企业要求第h大类产品仓库容量的保证率为βfh。令该策略下第h大类产品分配的仓库容量为 Xfh，则由 P(Zh≤Xfh)=βfh得：

其中，αfh为分类随机储存策略下第h大类产品仓库容量的安全系数，等于βfh对应的标准正态分布分位数。

因此，分类随机储存策略下整个仓库储存容量需求为：

到了大年三十晚上，麦村的大人小孩正在屋外放鞭炮焰火呢，突然发现癞阿小的那间破草屋着火了，那火烧的，火红，灿烂，那些不更事的孩子从未见过这么大的焰火，无不兴高采烈，拍手叫好。只有村里的男人和女人心里清楚这是怎么回事。

命题1 在同样的产品储存需求情况下，假定仓库总体的容量保证率要求为β，则：

（1）不同储存策略的仓库容量需求并不相同，且Xd≥Xf≥Xs；

（2）在分类随机储存策略下，如果在原有分类基础上将其中任意两大类产品合并，则需要的仓库容量X′f满足下述关系式：Xd≥Xf≥X′f≥Xs；如果将其中任意一大类分拆为两类，则需要的仓库容量X″f满足下述关系式：Xd≥X″f≥Xf≥Xs。

证明：这里只证明Xd≥Xs，其余命题内容证明过程类似。显然，在定位储存策略下，为保证仓库整体容量保证率不低于 β，则产品i分配的仓库容量保证率必须满足βdi≥β=βs，因此，公式（2）中的 αdi一定大于或等于公式（3）中的αs。

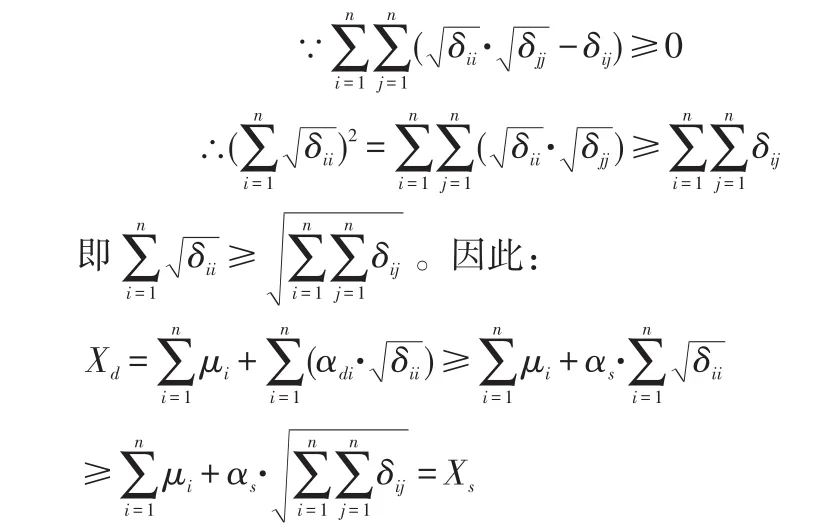
证毕。

命题2 给定仓库容量，在同样的产品储存需求情况下，采用定位储存策略的仓库容量保证率最低，采用随机储存策略的仓库容量保证率最高，而分类随机储存策略的仓库容量保证率处于二者之间。

证明：类似于命题1，证明略。

命题1表明，同样的仓库容量保证率下，不同储存策略需要的仓库容量并不相同，因此，在确定仓库容量时应该考虑将来的储存策略。

命题1第2部分和命题2表明，当仓库已经建成、容量给定的情况下，企业可以根据本文提出的仓储容量需求模型选择合适的储存策略。比如，如果企业仓库容量比公式（2）的计算结果大，则为提高作业效率、减少产品间相互影响可以考虑采用定位储存策略；而如果仓库容量比公式（2）的计算结果小但比公式（3）的结果大，则可以考虑采用合适的分类随机储存策略。当然，如果仓库容量确实太小，而又不能拓展仓储空间时，则只有采用随机储存策略。

4 算例分析

假设某仓库准备储存四种产品，根据经验可知未来其储存量服从多元正态分布，即Y=(Y1,Y2,Y3,Y4)T～N4(μ,Σ)，其中：

假设要求整个仓库容量的保证率β=95%。说明：上述储存量都是指转换为标准储存单元后的储存数量。

4.1 定位储存策略

为分析方便，假设各种产品的容量保证率均相同。为使仓库整体容量保证率达到95%，容易证明每种产品的容量保证率为=98.73% ，即 βd1=βd2=βd3=βd4=98.73% 。查标准正态分布表得，98.73%对应的分位数为2.235，即αd1=αd2=αd3=αd4=2.235。由公式（1）得，Xd1==10+2.235×10≈32。同理，X2≈19；X3≈42；X4≈27。

因此，四种产品在定位储存策略下的储存容量需求分别为32、19、42和27，合计120个储位。

4.2 随机储存策略

随机储存策略下为使仓库容量保证率达到95%，则查标准正态分布表得对应的分位数为1.645，即仓库容量的安全系数αs=1.645，代入公式（3）得，随机储存策略下仓库容量需求为Xs=10+8+20+9+1.645·≈79，即需要79个储位。

4.3 分类随机储存策略

假设根据产品特性将第1、2种产品分为一大类，将第3、4种产品归为另一大类。同时，与定位储存策略类似，假设每大类产品的仓库容量保证率均相同。为使仓库整体容量保证率达到95%，容易证明每大类产品的仓库容量保证率为=97.47%，即 βf1=βf2=97.47%，对应的标准正态分布分位数为1.955，即 αf1=αf2=1.955。

因此，由公式（4）得，第一大类产品的仓库容量需求为：

第二大类产品的仓库容量需求为：

即：为保证仓库容量保证率达到95%，第一大类和第二大类产品的仓库容量需求分别为43和49个储位，合计需要91个储位。易见120＞91＞79，即上述算例分析结果与命题1结论一致。

5 结论

本文研究表明，在相同的产品储存需求和仓库容量保证率下，定位储存策略需要的仓库容量最大，随机储存策略需要的仓库容量最小，而分类随机储存策略所需要的仓库容量介于二者之间。同时，除非企业在仓库运营管理中采用随机储存策略，否则在仓库建造时传统地以总储存量为基础分析计算出的仓库容量往往较小，不能够满足其他储存策略下的产品储存要求。因此，企业在设计和建造时仓库，应该考虑将来的储存策略，并基于储存策略选择合适的仓库容量。

[1]肖建,郑力.检修备品库的货位优化模型[J].清华大学学报(自然科学版),2008,(11):1883-1886.

[2]陈璐,陆志强.自动化立体仓库中的储位分配及存取路径优化[J].管理工程学报,2012,(1):42-47.

[3]戴韬,郑欣.基于分类随机策略的立体仓库货位优化研究[J].物流技术,2012,(9):259-261.

[4]Tompkins J,White J,Bozer Y,et al.Facilities planning[M].New York:Wiley,2010.

[5]王素华，邓正华.仓储与配送管理[M].重庆:重庆大学出版社,2012.

[6]任雪松,于秀林.多元统计分析[M].北京:中国统计出版社,2011.