基于直觉模糊和TOPSIS法的网络课程评价*

胡 景，张武威

(三明学院)

0 引言

随着MOOC(Massive Open Online Courses(大规模开放网络课程))在全球迅速兴起，网络课程与传统课程相结合的混合式学习成为主要学习方式.凤凰网讲堂“2012年最受欢迎中国网络课程评选”，将现有网络课程进行爬梳整理，评选标准从价值、视角、责任、探索开展，对我国网络教育综合评判及发展前景的综合预期，收到良好效果.目前，我国不少网络课程还处于小规模应用阶段，这些网络课程建设及使用情况怎样，如何挑选适宜的课程，这些都需要通过客观科学的评价来检验与引导.网络课程评价是一个客观的过程，它要应用科学的工具，来确认和解释网络课程的效果，衡量它们的有效程度，以便为网络课程的选择和改进做出有根据的决策.目前网络课程评价主要依据评委专家的主观判断来进行，这种方法直观简洁，但具有随意性和模糊性.

为有效解决评价过程中存在的主观模糊信息，论文采用序关系与直觉模糊法来表示评价指标权重和指标值，通过扩展TOPSIS法来全面、细致地展开评价，从而提高评价结果的客观科学性.

1 网络课程

1.1 建立网络课程评价指标

按照中国教育信息化技术标准CELTS－22《网络课程评价规范》，网络课程评价体系的核心是“课程内容、教学设计、界面设计、技术便捷与安全性”4个指标［1］.论文借鉴这个评价体系，建立评价指标见表1.

表1 网络课程评价指标

1.2 选取专家并设计其评价权重

评委由学科、计算机、教育学及教育技术者方面的专家及学生代表组成［2］.评委因其知识结构及职业结构、认识角度的差异对评价对象会产生不同的判断.经专家讨论，各评委的权重设置见表2.

表2 评委权重值表

1.3 利用序关系分析法确定评价因素(子因素)权重

评价指标权重的确定是前提问题.论文采用序关系分析法来确定指标权重［3］，其优点是:以评价者经验主观评价为基础，通过序关系分析法对其主观评价进行数学的运算，以获取客观指标权重.主要步骤如下:

(1)指标序关系的确定

定义1.1:若评价指标di相对于评价准则Z的重要性程度大于(或不小于)dj时，则记为di≻dj，若评价指标相对于评价准则存在关系式:≻≻…≻，则评价指标d1，d2，…，dm之间按“≻”确定了序关系.其中表示{di}按“≻”关系排序后的第i个评价指标(i=1，2，…，m).为书写方面，仍记为:

(2)dk－1和dk之间相对重要程度的判断.在评价准则Z下，指标dk－1和dk的重要程度之比wk－1/wk的判断为

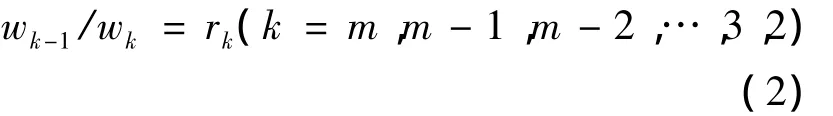
(3)权重系数wk的计算.若评价专家给出rk的理想判断，则有 wk－1=rkwk，文章 rk值参考表3.

表3 rk的赋值

2 直觉模糊的TOPSIS算法

2.1 直觉模糊

定义2.1 设是非空集合，则称A={〈x，μA(x)，νA(x)〉x∈X}为直觉模糊集，其中μA(x)和νA(x)分别表示X上的元素x属于A的隶属度和非隶属度，称 πA(x)=1－μA(x)－νA(x)为直觉模糊不确定数或犹豫度，0≤πA(x)≤1.

定义2.2 设非空有限集合x上A={〈x，μA(x)，νA(x)〉x∈X}，B={〈x，μB(x)，νB〉x∈X}2个直觉模糊集，则其之间存在以下运算;

(1)A=B当且仅当μA(xi)=μB(xi)和νA(xi)= νB(xi);

(1)A≤ B当且仅当 μA(xi)≤ μB(xi)和νA(xi)≤ νB(xi);

(3)A+B={〈x，μA(xi)+ μB(xi) －μA(xi)μB(xi)，νA(xi)νB(xi)〉}

(4)λA ={〈x，1 － (1 － μA(x)〉λ，(νA(x))λ}，其中 λ ≻0.

定义2.3 设非空有限集合X上A={〈x，μA(x)，νA(x)〉x∈ X}，B={〈x，μB(x)，νB(x)〉x∈X}，2个直觉模糊集，则A，B之间距离定义为:

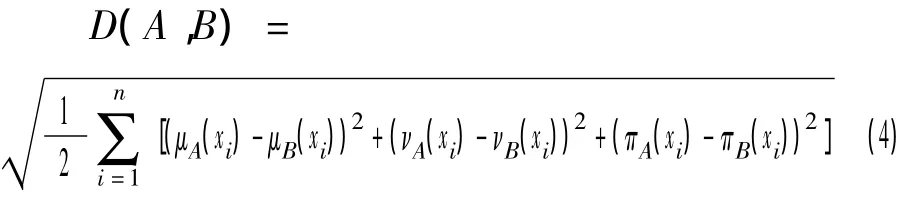
2.2 基于直觉模糊的TOPSIS算法

TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)的全称是逼近于理想值的排序方法，是简洁实用的多目标综合评价方法［4］.其基本原理是:把综合评价的问题归一为规范化矩阵，找出多个目标中正理想目标和负理想目标，然后检测评价对象与两者的距离，从而获得评价对象与理想解的贴近值，按理想解贴近值的大小排序，以此作为评价目标优劣的依据［5－6］.

基于直觉模糊的TOPSIS算法步骤方法如下:

(1)构建每个评委的直觉模糊矩阵

设 C=(c1，c2，…，cn)是n个评价对象集，D=(d1，d2，…，dm)是m个评价指标集，E=(e1，e2，…，el)是l个评委集，则第k个评委的直觉模糊矩阵Vk为:

(2)建立加权模糊矩阵

运用定义2.2中的运算(4)计算加权矩阵，第k个评委的加权直觉模糊集:

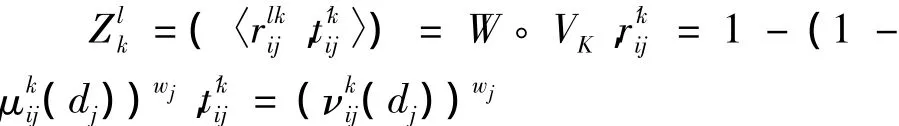
上式计算出每个评委为评价对象的加权矩阵，最后还要结合评委权重建立综合权重矩阵，假设评委权重集是W*，则第i个评价对象在第j个评价指标加权直觉模糊值为，综合加权矩阵 z=(〈rij，tij〉n×m.

(4)运用定义3中的求直觉模糊集的公式，计算每个评价对象与正负理想集间的距离和

(5)计算评价对象与理想解的贴近值，dj=

(6)依据贴近值的大小排序，贴近值越大则评价对象越优.

3 实证研究

3.1 研究开展步骤

基于序关系和直觉模糊的TOPSIS网络课程评价是一个质性评价逐步量化的过程，其操作流程如图1所示.

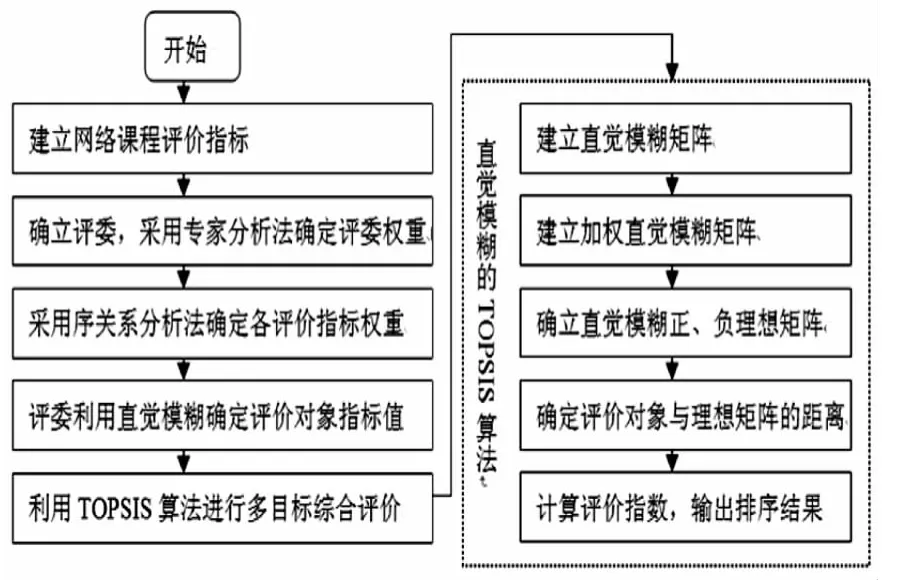
图1 基于序关系和直觉模糊的TOPSIS网络课程评价流程

3.2 具体操作步骤

(1)评委使用序关系分析法计算指标权重

一级评价指标的序关系、评价指标重要性标度及整体计算结果见表4，序关系列给出评委对指标重要性的比较认识［7］，通过公式 wk－1=rkwk(k=m，m － 1，…，3，2)可得，再根据 wm=可得出，由于)表示的序关系(d2，d1，d4，d3)的权重向量，则 W=(d1，d2，d3，d4).借助 EXCEL 工具 sqrt，geoman等函数快速求解，该文采用几何平均数为权重，指标权重集 W=(0.2586，0.3973，0.1852，0.1498)，结果见表4.

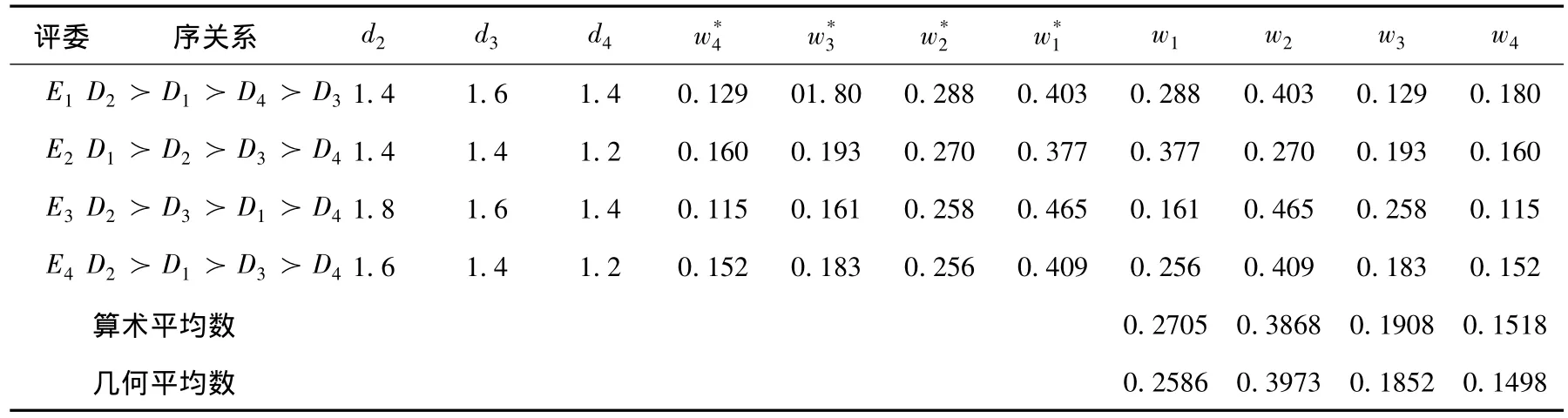
表4 评价指标权重结果表

(2)建立模糊评价集

论文选取三门网络课程C1、C2和C3为评价对象，采用表1的评价指标，由表2中的五位评委对课程进行评价，其评价的数据均为直觉模糊值，见表5.

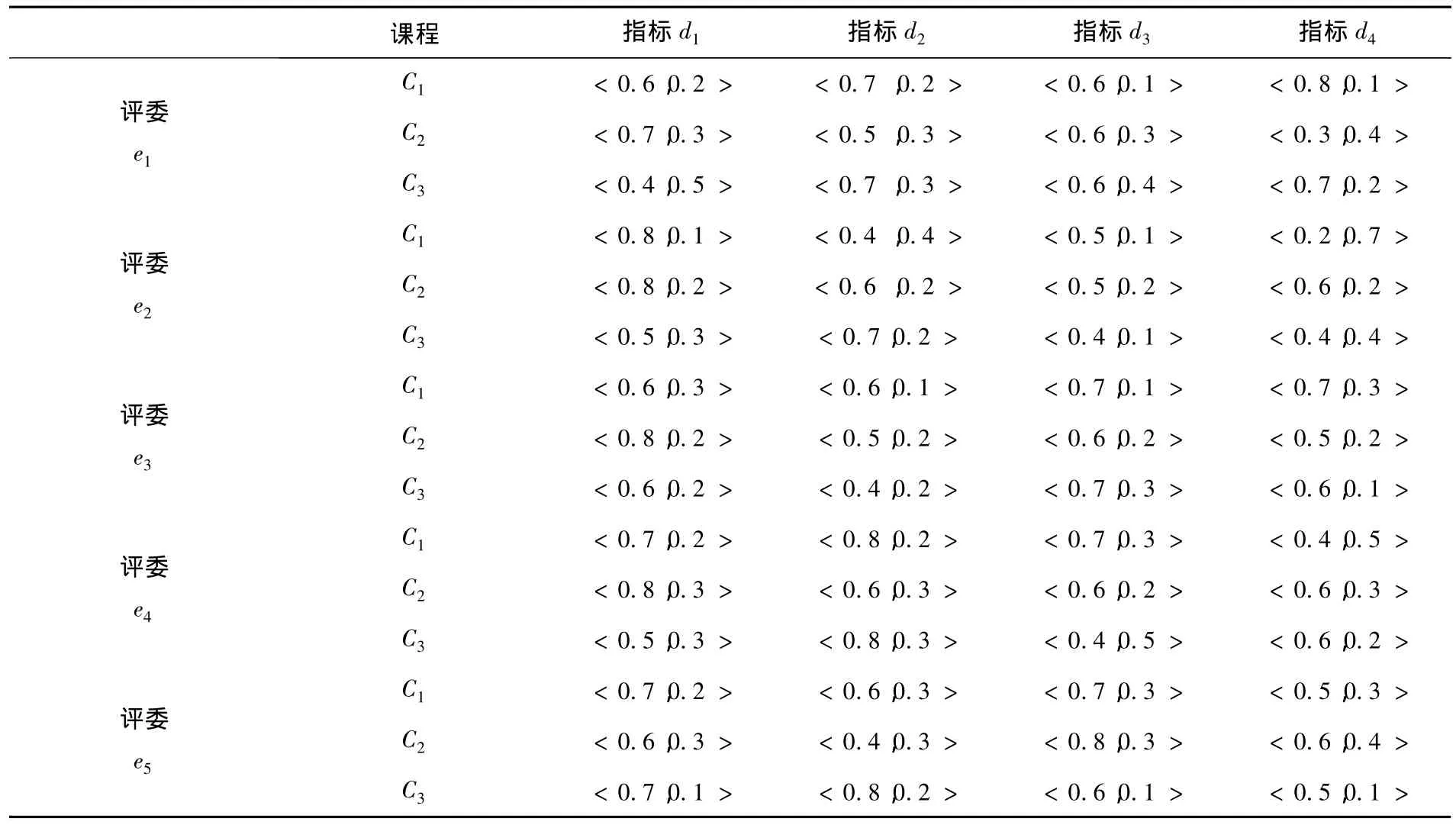
表5 五评委四指标三课程的直觉模糊数据

(3)根据表4，建立指标加权矩阵

根据表2，将评委的权重进行计算，得到综合加权矩阵:

(4)确定正负理想解

(5)三门课程距离正负理想解的距离

(6)贴 近 度 D =(0.57050.3548 0.6459)

根据贴近度，得出课程C3最优，其次课程C1，最后是 C2.

4 软件实现

根据以上算法模型，可通过Matlab或Visual(basic，c++等)平台自动化地进行评价［8］.主要思想:设计多维数组表达矩阵，采用多层循环计算，后台利用数据库，编出相应的计算机程序及软件，前端利用软件控件或按钮设计人机交互操作界面，形成网络课程评价的支持系统，以便提高计算效率.论文利用Visual Foxpro实现评价系统，评委通过输入评价数据，管理人员检查评委数据的有效性，数据合理后单击“排序”按钮，后台利用编写代码进行计算，最后将计算出的贴近度值显示出来，界面如图2所示.

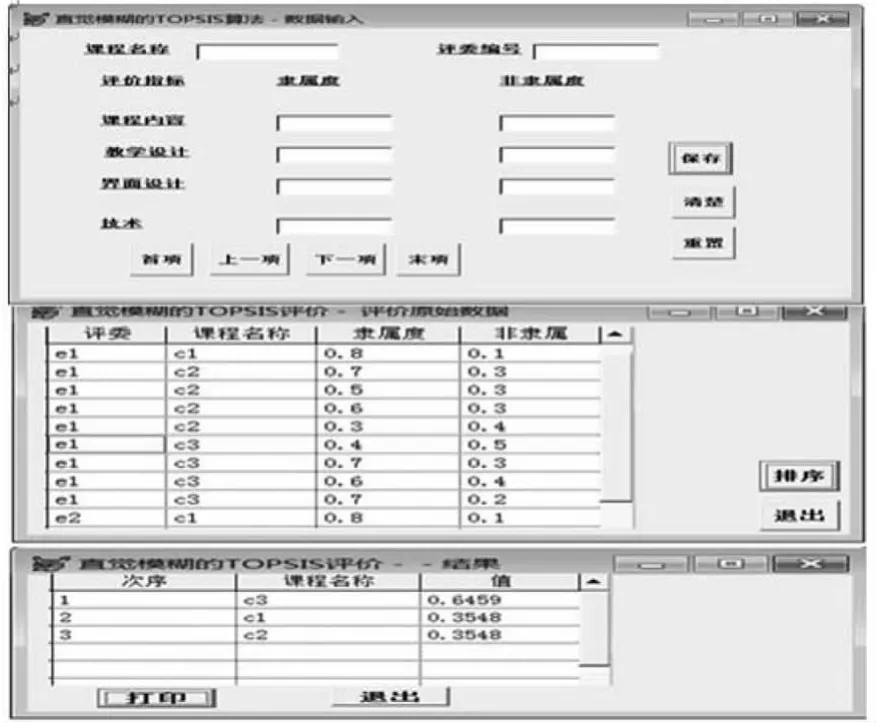
图2 直觉模糊的TOPSIS课程评价界面图

5 结束语

针对网络课程评价中评委判断可能受多种指标因素的影响，造成评判的主观性、模糊性，该文利用序关系分析法、直觉模糊集与TOPSIS算法联合使用，使得指标权重合理，评价结果精确科学，评价模型可行有效，评价方法在综合性，合理性，科学性等方面得到提高改进.

［1］ 乐玉玲.基于网络课程评价规范_CELTS_省略_22_1_的网络课程的设计与开发［D］.华中师范大学学位论文，2011.

［2］ 曹国强.模糊综合评价法在网络课程评价中的应用研究［J］.沈阳工程学院学报:自然科学版，2013(4):158－160.

［3］ 毛虎威.基于序关系的多属性决策［D］.中国科学技术大学，2012.

［4］ 张益.属性权重信息不完全的区间多属性TOPSIS法［J］.统计与决策，2007(7):142－144.

［5］ 李登峰.直觉模糊集决策与对策分析方法［M］.北京:国防工业出版社，2012.

［6］ 丁晓阳.基于TOPSIS扩展的直觉模糊多属性群决策［J］.海南师范大学学报:自然科学版，2012(12):355－359.

［7］ 王俊生.基于序关系分析法的网络课程模糊综合评价模型［J］.电化教育研究，2009(11):55－58.

［8］ 黄成.网络课程评价系统的研究与实现［J］.现代远距离教育，2010(6):69－71.