基于不规则区域分割及灰度排序分类的分形压缩算法
郑秋梅,赵 敏,王风华,赵景智
(中国石油大学计算机与通信工程学院,山东青岛 266580)
高压缩比和高保真性一直是图像压缩追求的目标。从20世纪五六十年代的预测编码、哈夫曼编码到七八十年代的变换编码和矢量量化编码,再到八十年代末的小波变换理论、分形理论[1]等都在追求这一目标。分形压缩算法以其高压缩比、任意尺度下的重构和快速解码等优越性成为当前研究热点;但基本分形算法需要庞大的匹配搜索运算,导致编码时间过长。目前主要通过缩小搜索匹配范围来提高编码速度,其中主要方法是对定义域块和值域块进行分类[2-3],把全局匹配搜索改为类内搜索匹配(分类搜索)。当前的分类搜索多以图像灰度值、纹理等单一特征作为分类依据[4],这样虽能在一定程度上缩小搜索范围,但编码时间仍不理想。笔者结合不规则区域分割压缩算法的思想,首次将脉冲耦合神经网络(pulse coupled neural network,PCNN)分割算法引入分形压缩,并且在分形压缩过程中,根据PCNN分割后所得二值图像的灰度值和原图像的灰度值两个特征联合分类,从而进一步缩小搜索匹配范围。
1 分形图像压缩的编码算法
20世纪80年代末,Barnsley[5]提出了基于迭代函数系统(iterated function system,IFS)的分形图像压缩理论。其基本思想是利用数据的自相似或自仿射特征,构造相应的IFS,然后记录其中相关参数,并最终用这些参数作为图像的编码进行存储和传输,从而只需少量数据就可恢复与原图像相近的图像,达到压缩图像数据的目的。其原理如图1所示。
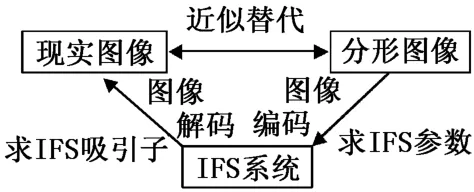
图1 分形编码原理图Fig.1 Fractal coding schematic
具体编码算法流程如下。
(1)将原图像分割成若干互不重叠的大小为B×B的Rang块(记作Ri)和若干可重叠的大小为2B×2B的Domain块。
(2)对2B×2B的Domain块进行收缩变换。即对每个Domain块中相邻的4个像素进行求和并取平均值,得到大小为B×B的Sub_Domain块,这种Sub_Domain的全体构成码本。
(3)获取分形码。对每个Rang块Ri都按以下三步在码本中寻找其最佳匹配Dm(i):
a)对每个Sub_Domain经过8个等距变换扩大为8个新的子块;
b)对每个Sub_Domain块及其8种等距变换得到的子块,与Rang块进行匹配,计算其MSE(Mean Square Error),计算公式为
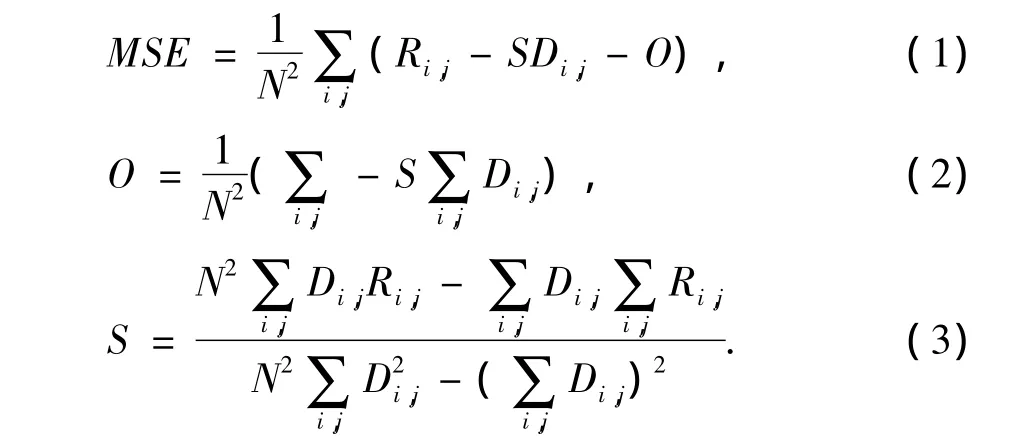
式中,Ri,j为 Rang 的像素值;Di,j为 Domain 块的像素值;S为比例因子;O为偏移量。若计算出的MSE小于给定的误差,则匹配成功,否则继续匹配,直到找出误差最小的匹配为止;
c)输出当前Rang块Ri的分形码,即参数Si、Oi、最匹配码字的下标m(i)以及等距变换序号。
(4)编码每个Rang块。对于每个Rang块Ri,重复步骤(3)直至所有Rang块完成编码为止。
(5)保存分形码,即得到分形编码文件。
由分形块编码过程可见,其耗时多主要是因为搜索匹配的范围过大。要减少匹配搜索时间,就要缩小搜索匹配范围。常用的分类法多以图像的单一特征作为分类依据,但由于Domain块数量巨大,在相应类中搜索最佳匹配块所需的时间仍然很长,为解决这一问题,结合不规则区域分割编码思想对分形压缩算法进行了改进。
2 算法改进
2.1 算法描述
基于不规则区域分割及灰度排序分类的分形压缩算法((PCNN-GRAY)):先对原图像进行不规则区域分割;然后对这些区域进行分形压缩编码,将分形压缩中的全局搜索匹配改为在具有较高相似性不规则区域内的搜索匹配,以达到缩小搜索匹配范围的目的;最后在分形压缩过程中加入基于图像灰度值排序分类的方法,进一步缩小搜索匹配范围。
2.1.1 基于不规则区域分割编码
基于不规则区域分割编码技术的思想是先让分割区域(或纹理)与原始图像对应部分在视觉意义上最大程度地接近,再对这些区域(纹理)进行编码[6]。然而,与传统规则的分块相比,不规则区域分割在编码时需要增加边缘的位置信息,这样不仅增加了额外的编码数据量及编码时间,且这些边缘信息不能大幅度压缩。本文中利用不规则区域分割编码的思想,首先对原图像进行不规则区域分割,然后在分割区域中采用分形压缩算法,从而将分形压缩中的全局搜索匹配改为区域搜索匹配,达到缩小搜索匹配范围的目的。
由于PCNN分割模型对图像分割完全依赖于图像的自然属性,且各个分割区域的像素不仅具有相似的灰度值,在空间上也具有一定的相似性,同时原图像经过PCNN分割后得到的二值图像中,各个不规则分割区域的像素具有灰度值相似的特征,可作为分形压缩算法中搜索匹配的分类依据。
2.1.2 PCNN分割模型
PCNN模型是一种基于神经生理学的模型,它由基本神经元组成,其结构如图2所示。
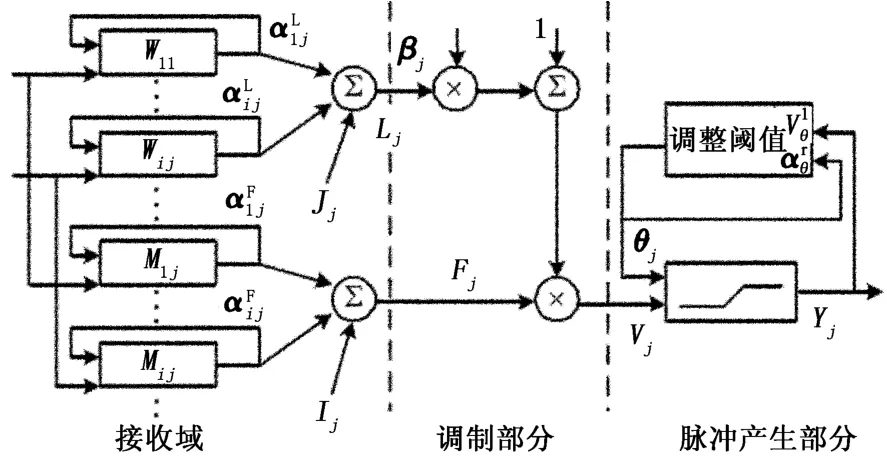
图2 PCNN神经元结构图Fig.2 Structure of PCNN neuron
每个神经元的具体运算如下:
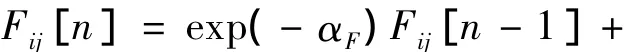
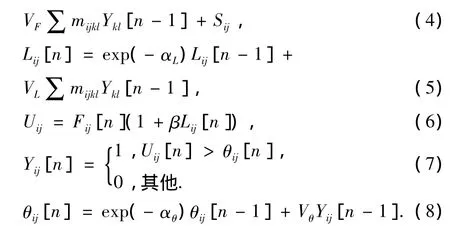
式中,S表示输入激励,一般为像素点(i,j)的灰度值,每个像素点对应一个神经元;F对应神经元的输入部分,L是连接输入,U对应神经元内部活动项,Y和θ分别为神经元的输出和动态阈值,M、W对应神经元的内部连接矩阵;V为反馈放大系数;α为衰减时间系数;β为连接系数。当利用PCNN进行图像分割时,灰度值大的像素点所对应的神经元先点火,输出脉冲1,该像素点周围具有近似灰度值的其他像素点所对应的神经元在下次迭代时受连接输入影响也被激活输出脉冲1,则具有相似灰度值的区域因受连接域的影响而同步激活,从而实现分割[7-9]。
本文依据PCNN分割后得到的二值图像中各个分割区域的像素具有相似灰度值这一特征对原图像块进行分类,从而避免了对边缘信息进行编码。由于二值图像灰度值只有0、1两种情形,所以划分后二值图像块R的灰度均值有3类:均值HR=0;均值HR=1;均值0<HR<1。在分形压缩时,原始图像块根据对应的二值图像块灰度均值分类结果被分成3类,搜索范围也由全局搜索改为分割区域搜索,最终达到减少算法编码时间的目的。该方案虽缩小了分形压缩算法的搜索匹配范围,但因为分类特征单一,编码时间仍不理想,所以本文又在PCNN分类基础上引入了基于图像灰度值排序分类。
2.1.3 灰度排序分类
图像灰度值排序分类是将图像Rang块和Domain块分割为上左、上右、下左、下右4个部分(图3),并依次记为 A1、A2、A3、A4,计算每个 Ai块的灰度均值μi。则对任意Rang块和Domain块都可通过“反射-旋转”变换,使μi值排列属于以下3种情况之一,从而将Rang块和Domain块分成3大主类[10]。
主类 1:μ1≥μ2≥μ3≥μ4;
主类 2:μ1≥μ2≥μ4≥μ3;
主类 3:μ1≥μ4≥μ2≥μ3。
在本文算法中,对PCNN分割区域分类处理后的图像块再进行灰度排序分类,每一类又被分成3类,则Rang块和Domain块图像块被分成9类,在匹配时每个Rang块只需在相同类别的Domain块中寻找相似匹配块,进一步缩小了搜索范围。同时,为了排除对解码图像质量造成的影响,改进算法在依据二值图像块的灰度均值对原始图像块进行分类时,增加灰度均值分类的重叠,以提高图像的解码质量。多次实验表明,二值图像灰度均值分类取为HR≤0.4;HR≥0.6;0.1≤HR≤0.9时实验结果最佳。
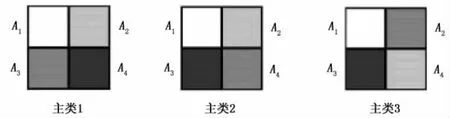
图3 按块的灰度均值分类情况Fig.3 Classification by average of gray value
2.2 算法流程
(1)对原图像I进行PCNN分割,输出二值图像I';
(2)分别将I'和I分割成若干互不重叠大小4×4的BWRang块和Rang块(其中BWRang为二值图像值域块,Rang为原图像值域块);
(3)分别将I'和I分割成若干可重叠、大小为8×8的BWDomain块和Domain块(其中BWDomain为二值图像定义域块,为Domain原图像定义域块);
(4)对于8×8的Domain块进行收缩变换。即对每个Domain块中相邻的4个像素灰度值进行求和并取平均值,得到大小为4×4的Sub_Domain块;
(5)根据每个BWRang块的像素值和BWDomain块的像素值分别将Rang块和Domain块分成3类:均值HR≥0.6称为1值块类;均值HR≤0.4称为0值块类;均值HR在0.9≥8≥0.1称为中值块;
(6)将第(5)步中得到的每类按灰度排序分类法再分成3大类,则每个Rang块和Domain块被分成了9类;
(7)对每个Rang块,根据分类结果在相同类别的Domain块及其8种等距变换的子块中进行匹配计算;
(8)保存匹配成功时的变换编号、比例因子、偏移量及Domain块位置。
3 实验结果分析
实验采用256×256×8的LENA和Pepper图像,将原图像分割成互不重叠的4×4块,用Matlab7.0编程。将本文中提出的PCNN-GRAY算法与分形块压缩算法、灰度排序分类算法进行了对比实验(为对比说明,本文中也实现了仅基于PCNN分割的分类算法)。实验结果如表1所示。
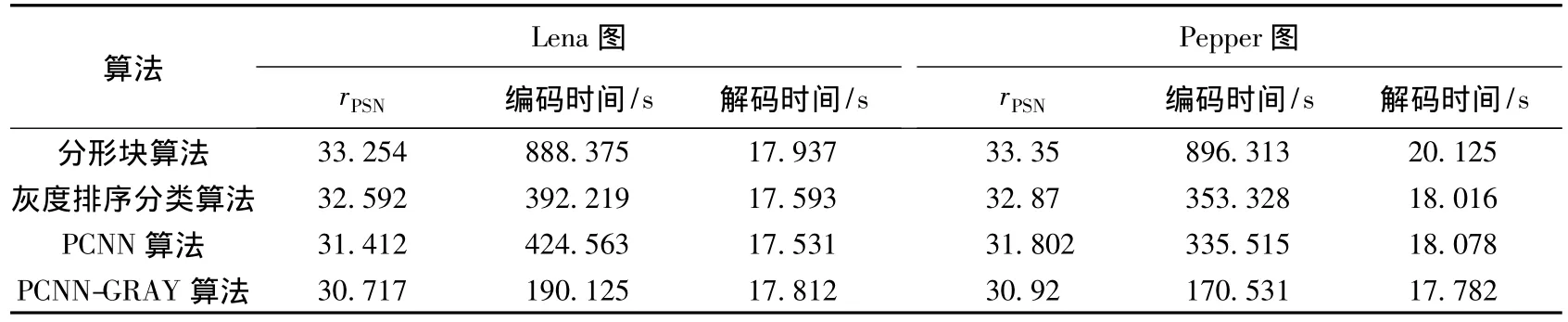
表1 不同算法的峰值信噪比rPSN及耗时Table 1 rPSNand time-consuming of different algorithms
由表1可以看出,同分形块算法和灰度排序分类算法相比,PCNN-GRAY算法中的rPSN虽有一定下降,但编码时间大幅减少。但图4(d)中有较明显的方块效应,为了消除方块效应,先对图像进行均值滤波处理,可是进行滤波处理后,图像会变得模糊,所以将原图像和滤波后的图像灰度值进行相加求平均,如图5所示。处理后的图像方块效应明显降低,而且优化过程不影响其编码过程的耗时,对解码时间的影响也不明显。

图4 不同算法解码图像效果Fig.4 Decoded image of different algorithms

图5 平滑处理后的图像效果Fig.5 Decoded image of algorithms after smoothing
4 结束语
结合传统的基于分类的分形压缩和不规则区域分割压缩算法的优势,首次将PCNN分割算法引入分形压缩,提出一种PCNN-GRAY算法,在尽量保证解码图像质量的前提下,大幅度缩小了搜索匹配范围,减少了编码时间。该算法可在图像压缩方面应用推广,但解码图像的质量仍不尽人意,需进一步改进。
[1] 孟宪伟,晏磊.图像压缩编码方法综述[J].影像技术,2007(1):6-8.MENG Xian-wei,YAN Lei.Image compression coding method review [J].Imaging Technology,2007(1):6-8.
[2] JACOBS E W,FISHER Y,BOSS Y D.Image compression:a study of the iterated transform method[J].Signal Processing,1992,29(3):251-263.
[3] 秦峰,吴征.分区IFS图像压缩编码[J].通讯学报,1997,18(5):1-7.QIN Feng,WU Zheng.Area-based IFS image coding[J].Communications,1997,18(5):1-7.
[4] 郑秋梅,吕兴会,时公喜.基于多特征集成分类器的人脸表情识别[J].中国石油大学学报:自然科学版,2011,35(1):174-178.ZHENG Qiu-mei,LÜ Xing-hui,SHI Gong-xi.Facial expression recognition based on multi-feature and combining multiple classifiers[J].Journal of China University of Petroleom(Edition of Natural Science),2011,35(1):174-1178.
[5] 李明水,欧珊瑚,张珩.分形图像压缩方法研究的新进展[J].工程图学学报,2004(2):143-152.LI Ming-shui,OU Shan-hu,ZHANG Heng.The progressof fractal image compression method research[J].Journal of Engineering Graphics,2004(2):143-152.
[6] 马义德,齐春亮,钱志柏,等.基于脉冲耦合神经网络和施密特正交基的一种新型图像压缩编码算法[J].电子学报,2006,34(7):1255-1259.MA Yi-de,QI Chun-liang,QIAN Zhi-bo,et al.A novel image compression coding algorithm based on pulse-coupled neural network and Gram-Schmidt orthogonal base[J].Acta Electronica Sinica,2006,34(7):1255-1259.
[7] 顾晓东,余道衡.PCNN的原理及其应用[J].电路与系统学报,2000,6(3):45-49.GU Xiao-dong,YU Dao-heng.PCNN1s principles and applications[J].Journal of Circuits and Systems,2000,6(3):45-49.
[8] 马义德,齐春亮,钱志柏,等.基于PCNN的不规则分割区域压缩编码[C].第十二届全国图象图形学术会议论文集,c2005.
[9] 黄晓莉,曾黄麟,王秀碧,等.基于脉冲耦合神经网络的图像分割[J].信息技术,2008,32(9):90-91.HUANG Xiao-li,ZENG Huang-lin,WANG Xiu-bi,et al.Image segmentation based on pulse-coupled neural network[J].Information Technology,2008,32(9):90-91.
[10] 郭京蕾,吴勇.基于分类方法的分形图像压缩[J].计算机工程与设计,2007,28(4):890-892.GUO Jing-lei,WU Yong.Fractal image compression based on classification method[J].Computer Engineering and Design,2007,28(4):890-892.

