小波奇异值分解的瞬变弱信号检测

徐彦凯，双 凯

(中国石油大学地球物理与信息工程学院，北京 102249)

在油气井下电磁脉冲数据传输中，有效信号具有暂态瞬变的特征。由于传输距离远，接收到的微弱有用信号往往被环境噪声所淹没。因此，有效检测瞬变弱信号是电磁脉冲数据传输的关键技术。小波分析是近些年发展起来的一种新的时频分析方法，小波变换能使信号能量集中在一些大的小波系数中;而噪声能量却分布于整个小波域内，对应的小波系数小。因此，小波阈值法可以较好地用于抑制噪声并检测信号。考虑到加噪信号对应矩阵的奇异值分解一定程度上可以反映矩阵的主要特征，实现噪声去除和信号提取，笔者将小波及奇异值分解相结合，实现微弱瞬变信号的检测。

1 小波变换及降噪应用

1.1 小波变换理论

设ψ(t)∈L2(R)，若ψ(t)为母小波，其傅里叶变换Ψ(ω)满足条件:

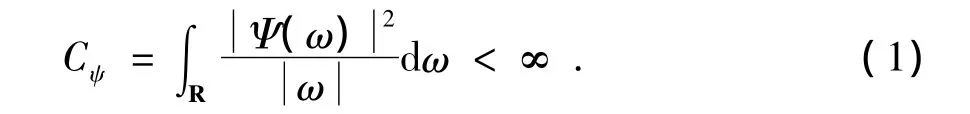
将ψ(t)进行伸缩和平移，得到小波基函数

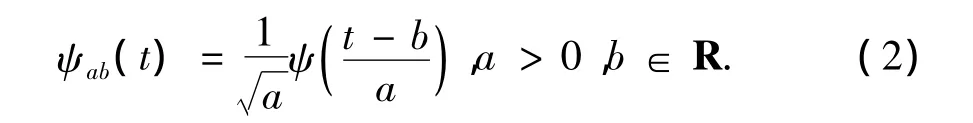
其中a为尺度(伸缩)因子，b为平移因子。信号f(t)的连续小波变换定义［1］为

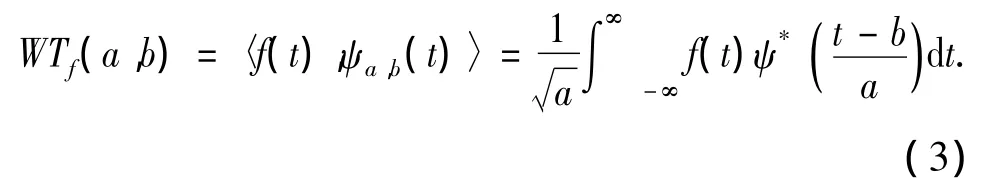
对 a、b 进行二进离散化，即 a=2j，b=2jk，j，k∈Z，得到的二进小波变换为

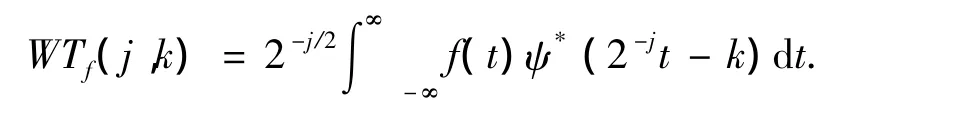
其逆变换为

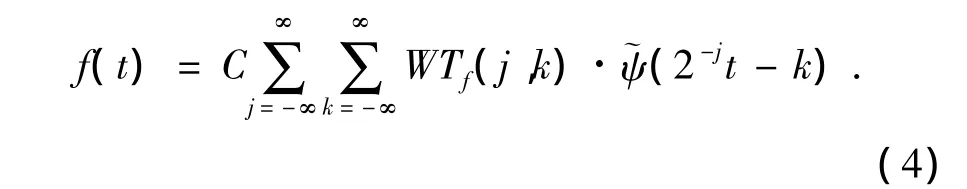
Mallat算法实现了二进小波的快速分解与重构［2］，分解公式为

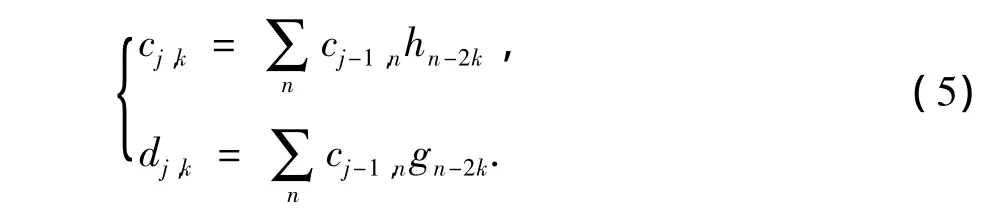
重构公式为

式中，cj，k为尺度系数;dj，k为小波系数;h、g、～h、～g 分别为低通和高通分解与重建滤波器;j为分解层数。

1.2 小波阈值法降噪检测技术

由于小波变换能使信号的能量集中在一些大的小波系数中，而噪声能量却平均分布于整个小波域内，对应的小波系数小。应用信号与噪声小波系数的特点对信号降噪，降噪步骤［3］如下:

(1)确定小波基函数和小波分解最大层数，应用式(5)对信号进行J层小波分解得到小波系数和尺度系数。

(2)确定每层小波系数的阈值，根据每层阈值按阈值函数形式对小波系数进行处理，把保留下来的作为降噪后信号的小波系数。

(3)利用式(6)对信号进行重构，并对降噪后信号检测。

上述步骤中，分解尺度、阈值函数和小波基函数的合理选择对信号检测至关重要。

2j尺度下小波伪频率f2j与小波中心频率fc的关系［3］:

式中，Δt为采样周期。

若信号的中心频率接近小波的伪频率，则会使此频率段的小波系数达到最大，从而有效地检测信号。研究的瞬变信号的频率集中在(0.3～1.1)×105Hz，db2小波的中心频率为0.6667 Hz，采样周期为1×10－6s，由式(7)可知，j=3和4的db2小波伪频率在信号的频率范围，所以确定小波分解最大层数为4。

常用的方法有硬阈值函数和软阈值函数，采用软阈值处理会对所有的小波系数都进行抑制，可使降噪后信号比较平滑，但对于提取具有突变特性的瞬变信号而言，对降噪后信号的平滑性没有要求，相反采用硬阈值方法能够更好地保留原信号的一些瞬变特征以便信号检测，所以采用硬阈值处理方法更为合适。

选择小波基函数时考虑正交小波变换后的数据不会出现冗余，并保证信号精确重构。因此选择几种有代表性的常用正交小波基:haar小波、coif1小波、sym2小波和db2小波，在此基础上进一步通过仿真试验对比选优。

1.3 仿真与分析

四种小波基下的重建信号见图1。

图1 四种小波基下的重建信号Fig.1 Reconstructed waveforms by four wavelet functiones

电磁脉冲传输的数字信号用图1(a)中的瞬变信号表示，该信号是一个持续时间短的暂态过程。通过电路分析，得到该信号的数学模型为

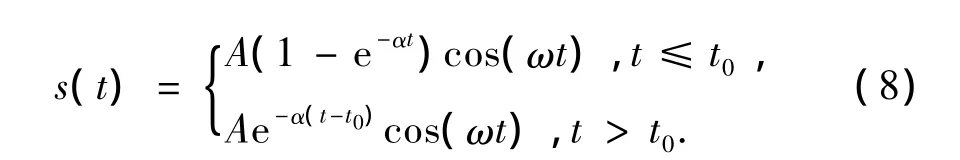
式中，A为信号幅度;ω为振荡频率;α为衰减因子，决定信号暂态过程的持续时间，其持续时间由电路参数决定;t≤t0为充电时间;t＞t0为放电时间。α=15，ω =4.7 × 105rad/s。

井下电磁脉冲信号传输中，噪声源主要有两大类:井下钻井环境产生的噪声和电子器件产生的电子噪声。钻井噪声频率范围为1～4 kHz。电子噪声在频域和时域上分布一致，是一种高斯白噪声［4］。由于钻井噪声可通过滤波的方法去噪，在此只考虑无法直接滤除的白噪声。

针对小波基的选取进行试验，试验中采用如图1(b)所示的－2.5 dB加噪信号，统一的4尺度分解，得到图1所示的4种小波基下的重构信号。比较图1中的(c)、(d)、(e)、(f)，可以直观地看出，针对本文研究的瞬变信号，db2小波的降噪效果最佳，sym2次之，coif1小波最差，因此选择db2小波基。

由图1(b)信号作4尺度db2小波分解的各尺度系数如图2所示。从图2看出，无法从j=1，2的小波系数中区分信号和噪声，因此重构时将j=1，2的小波系数全置零，保留 j=3，4中大于阈值 λ=σ的小波系数。

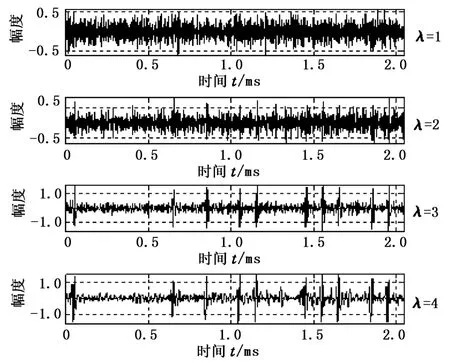
图2 db2小波分解各尺度系数Fig.2 Scale coefficients with db2 wavelet

图1(c)表明，在高信噪比的情况下，小波阈值法可以实现信号的检测，但从图3所示的 －8.5 dB加噪信号的db2小波重建信号可以看出:在(0.1～0.2)ms和(0.7～0.8)ms处没有信号，但在相应位置重构信号的幅度较大。

因此，为了更好地检测强噪声中的弱信号，需要将j=3，4信号和噪声的小波系数进一步分离。

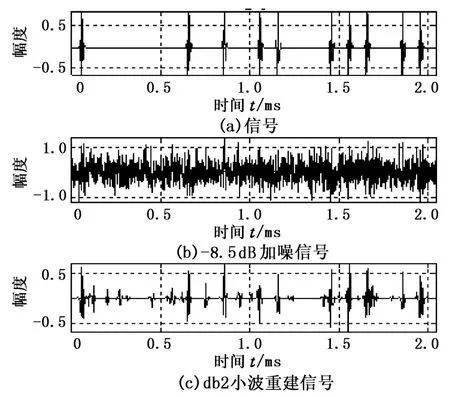
图3 -8.5 dB加噪信号的db2小波重建信号Fig.3 db2 WT reconstructed waveform with-8.5 dB SNR

2 奇异值分解降噪

2.1 奇异值分解理论

设矩阵Hm×n(m≤n)秩为r，则存在两个正交矩阵U、V和对角矩阵D，使得下式成立［8］:

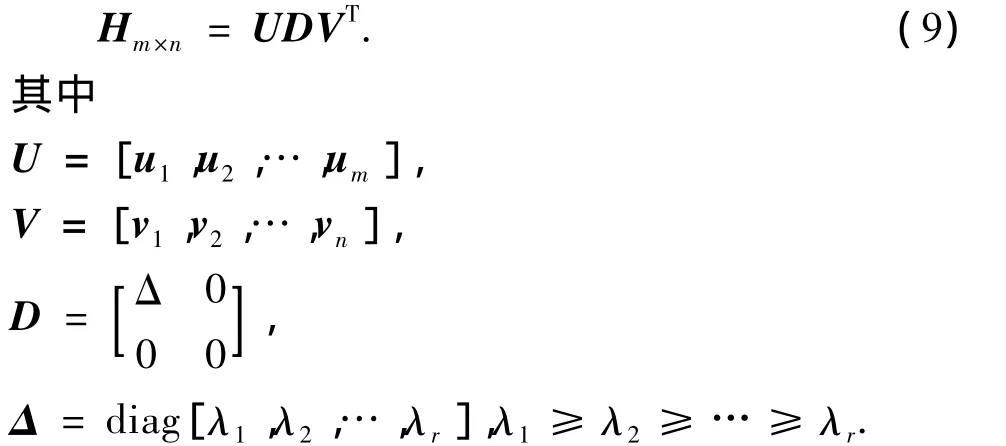
式中，λi为矩阵H的奇异值;ui和vi是λi的特征向量为特征项。奇异值分解是一种代数特征提取方法，能找到矩阵各向量之间的内在本质属性。因此加噪信号序列的奇异值分解可以提取序列主要特征，实现信号降噪和检测。其步骤如下:

(1)Hankle矩阵生成。设加噪信号序列为X=［x0，x1，…，xN－1］，构造 Hankle 矩阵 H［5-7］

矩阵H的行数L、列数J及序列X的长度N之间应满足

(2)矩阵奇异值分解。对矩阵H进行奇异值分解，λ1，λ2，…，λr为矩阵 H 的按降序排列的非零奇异值，即 λ1≥ λ2≥ … ≥ λr。

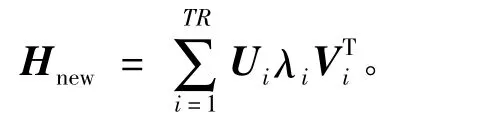
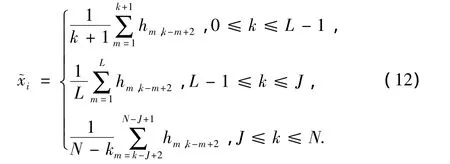
由式(12)重建信号并检测有用信号存在与否。

2.2 参数选择

奇异值分解中，窗长L及保留特征值个数TR的选择影响降噪和检测效果。

本文首先选取TR=5，窗长L分别选取15、22、30、40、60，码元中有用信号的采样点数是 30，加噪信号的信噪比分别为－2.5、－5.5、－8.5、－9.5、－10.5、－11.5 dB，仿真得到如图4所示的SVD降噪峰值信噪比与窗长L的关系。

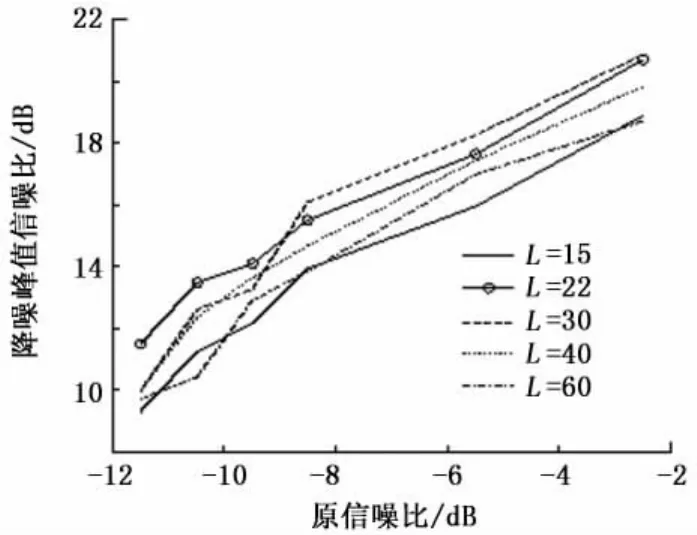
图4 窗长对SVD降噪峰值信噪比的影响Fig.4 Effect of window length on SVD-denoised PSNR

从图4看出:当原信噪比大于－8.5 dB，窗长L选取30效果最好;当原信噪比小于－8.5 dB，窗长L选取22效果最好;窗长L选取过大(L=60)或过小(L=15)降噪效果明显差。因此得出:①若原信噪比较大，选择窗长L等于码元中有用信号长度时效果最佳;②若原信噪比较小，选择窗长L比码元中有用信号的长度稍小些降噪和检测效果最好，这是由于信号末端采样值接近零，当噪声较强时，奇异值分解中这部分值的特征完全被噪声淹没造成的。

然后选取窗长L=22，保留特征值个数TR分别选取15、10、5、3、2，加噪信号的信噪比分别为 －2.5、－5.5、－8.5、－9.5、－10.5、－11.5 dB，得到如图5所示的SVD降噪峰值信噪比与保留特征值个数TR的关系。

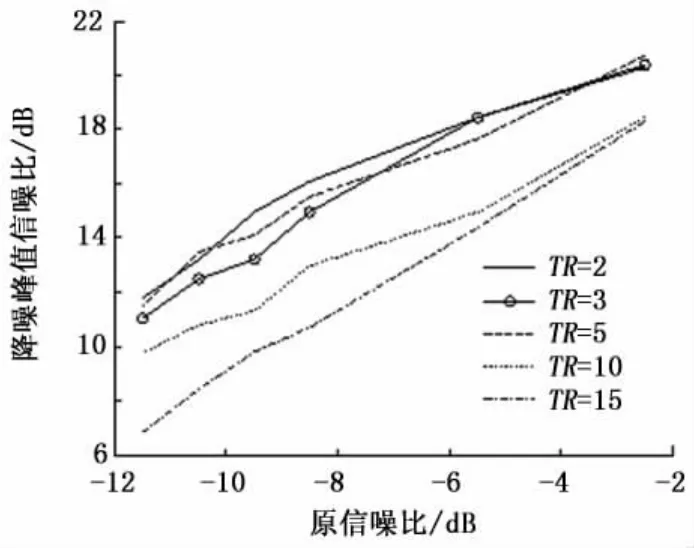
图5 保留特征值个数TR对SVD降噪峰值信噪比的影响Fig.5 Effect of main singular values1 number on SVD-denoised PSNR

从图5看出:①降噪后峰值信噪比随着原信噪比的减小而减小;②保留特征值个数TR=2峰值信噪比最高，检测效果也最佳;③原信噪比越小，TR的选择对降噪后峰值信噪比的影响越大，这是由于奇异值分解中大部分特征值已经体现不出信号的特性。

2.3 仿真与分析

在研究奇异值分解参数选择的基础上，采用奇异值分解方法对－8.5 dB加噪信号检测，其中选择参数L=22，TR=2，仿真结果如图6所示。

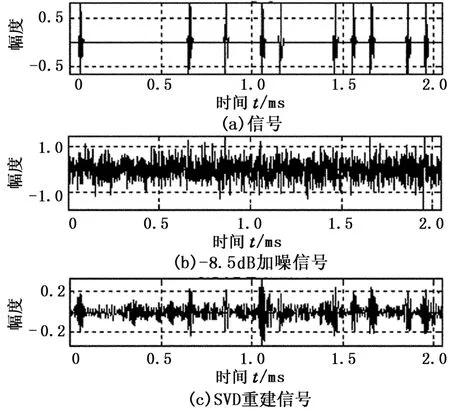
图6 -8.5 dB加噪信号的SVD重建信号Fig.6 Reconstructed waveform by SVD method with-8.5 dB SNR

比较图3(c)和图6(c)可知:从检测的角度看，奇异值分解比小波降噪后判决出错的概率小;但从输出信噪比看，奇异值分解比小波降噪差。

3 小波奇异值分解降噪检测

通过上述分析可知，若将小波和奇异值相结合［7-8］会使信号和噪声的小波系数更好地分离，检测效果更佳。具体方法是:首先将信号作小波分解，再对小波分解系数作奇异值分解，最后通过阈值法保留信号小波系数并重建降噪信号，利用重建信号进行信号检测。

图7(a)和图7(b)分别为信号和－8.5 dB加噪信号，采用小波阈值、奇异值分解及小波奇异值三种方法对图7(b)加噪信号降噪，降噪结果分别如图7(c)～(e)。可以看出:仅采用奇异值分解的图7(d)降噪效果最差;采用小波降噪的图7(c)虽然效果较好，但在没有信号的(0.1～0.4)ms、和(0.5～0.6)ms处的重构信号的幅度较大;采用小波奇异值方法的图7(e)则可以准确检测信号的存在。因此与小波阈值法和奇异值法相比，小波奇异值法降噪和检测效果最佳。

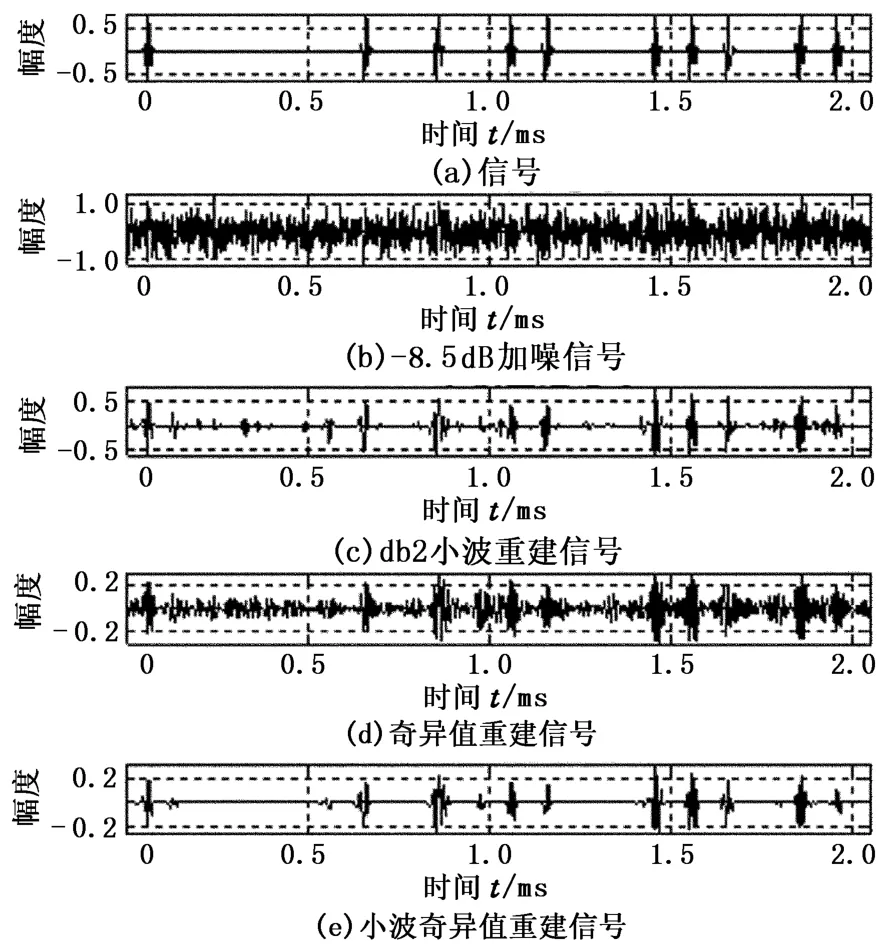
图7 -8.5 dB加噪信号的三种方法重建信号Fig.7 Reconstructed waveforms by three methods with-8.5 dB SNR

4 结束语

针对油气井下电磁脉冲数据传输中瞬变弱信号的检测，研究了小波阈值法和奇异值分解及参数选择。在此基础上提出了小波与奇异值分解相结合降噪检测信号的方法。仿真结果表明，该方法能更好地区分信号和噪声，获得了更好的降噪和检测结果。

［1］ IMTIAZ H，FATTAH S A.A wavelet-based dominant feature extraction algorithm for palm-print recognition［J］.Digital Signal Processing，2013，23(1):244-258.

［2］ TOUBIN M，DUMONT C，VERRECCHIA E P，et al.Multi-scale analysis of shell growth increments using wavelet transform［J］.Computers ＆ Geosciences，1999，25(8):877-885.

［3］ 臧玉萍，张德江，王维正.小波分层阈值降噪法及其在发动机振动信号分析中的应用［J］.振动与冲击，2009，29(8):57-60.ZANG Yu-ping，ZHANG De-jiang，WANG Wei-zheng.Per-level threshold de-noising method using wavelet and its application in engine vibration analysis［J］.Journal of Vibration and Shock，2009，29(8):57-60.

［4］ 肖红兵，杨锦舟，鞠晓东，等.V系统在随钻声波测井数据降噪中的应用［J］.中国石油大学学报:自然科学版，2009，33(2):58-62.XIAO Hong-bing，YANG Jin-zhou，JU Xiao-dong，et al.Application of V-system in acoustic logging while drilling data de-noising［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(2):58-62.

［5］ ALONSO F J，DEL CASTILLO J M，PINTADO P.Application of singular spectrum analysis to the smoothing of raw kinematic signals［J］.Journal of Biomechanics，2005，38(5):1085-1092.

［6］ ZHAO X，YE B.Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock［J］.Mech Syst Signal Process，2011，25(5):1617-1631.

［7］ JIANG Y H，TANG B P，QIN Y，et al.Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD［J］.Renewable Energy，2011，36(8):2146-2153.

［8］ 段礼祥，张来斌，王朝晖，等.柴油机振动信号的小波包奇异值降噪［J］.中国石油大学学报:自然科学版，2006，30(1):93-97.DUAN Li-xiang，ZHANG Lai-bin，WANG Zhao-hui，et al.De-noising of diesel vibration signal using wavelet packet and singular value decomposition［J］.Journal of China University of Petroleum(Edition of Natural Science)，2006，30(1):93-97.