基于CUDA的GPU条件分支分歧聚合优化策略

刘素芹，王 鑫，安仲奇，杨娜利，王俊爽

(中国石油大学计算机与通信工程学院，山东青岛 266580)

近年来由GPU作为加速部件的异构计算系统和技术，如CUDA［1］产生并得到发展。GPU擅长的SIMD(single instruction multiple data)执行方式提高了系统的计算效率，但当程序出现条件分支分歧时，会部分或完全退化成串行执行，性能损失严重。条件分支是控制程序执行流的基本方式，易大量出现，并且算法越复杂，对分支的利用就会越频繁。因此，需要优化GPU对条件分支的处理以更充分地发挥其并行计算的潜力。目前的研究主要集中在硬件层面设计线程调度器方面［2-5］，对普通用户而言实现难度较大，而利用现有体系结构从软件层面优化条件分支处理流程方面的研究还较少，因此笔者探索实现难度较低、可操作性较强的优化方法。

1 GPU条件分支处理机制分析

1.1 基于CUDA的GPU处理条件分支的机制

基于CUDA的GPU执行没有分支的语句时，线程束(warp［6］)中的线程按照SIMD的方式步调一致地执行，而遇到条件分支分歧时，处理过程则有所不同。对于较简单的IF-ELSE语句，PTX［7］汇编器将PTX语句只编译为GPU断言指令。此时GPU的断言设置指令处理IF语句的条件部分，并根据判断结果设置断言寄存器的各位，从而启用或禁用对应的SIMD道。当执行IF内部的语句时，操作被广播至所有SIMD道，但只有断言寄存器设为启用的道执行操作并流出结果，设为禁用的道并不执行操作也不保存结果。ELSE部分处理方式与之类似。分支语句执行结束后，SIMD道不再受断言影响，继续一致地执行后续指令。当SIMD线程中的所有道都选择了相同的路径时，不被执行的另一路径的指令将被直接跳过。

对于复杂控制流如嵌套条件语句，则需要混合使用断言指令、GPU分支指令和同步指令。此时，当分支分歧时，栈条目被压入分支同步栈，SIMD道转到目标指令执行。当分支收敛时，栈条目弹出，SIMD道转回栈条目地址且断言寄存器还原为上一层嵌套的掩码。

1.2 条件分支对计算性能的影响

SIMD执行方式处理条件分支时性能损失往往是显著的。如果条件分支嵌套较深，可能导致多数SIMD道空闲，比如假设每条分支路径的长度相同，两层嵌套将使效率降低至25%，三层嵌套进一步降低至12.5%。在最坏情况下，所有SIMD元素将串行执行，以 Fermi［8］架构为例，每两个时钟周期(SIMD线程宽度为32，执行单元宽度为16)只能有一条SIMD道流出有效结果，其他道都被阻塞［9］。下列IF语句和IF-ELSE语句是造成SIMD执行性能损失的两种基本条件分支语句结构。

(a)IF语句:

(a)只有一条分支路径，如果某一SIMD线程中的任意SIMD道需要执行IF内部的语句，则同一SIMD线程中所有的SIMD道都会经过这个分支路径，只是断言寄存器设为禁用的道不执行实际操作，因此部分计算资源闲置，性能有显著损失。(b)相当于两个(a)情况的叠加，同一SIMD线程中只有当所有SIMD道都选择相同的路径时才会少走一路分支路径，其他情况下所有SIMD道都会经过两个分支路径，程序性能损失为(a)的两倍。

1.3 GPU条件分支优化的研究现状

条件分支分歧对计算性能的影响主要是由GPU底层的处理方式造成的，因此现有优化方法多倾向于设计某种新硬件机制来重新调度SIMD道，避免在SIMD线程内发生分支分歧，使其在每步计算中更充分地利用计算资源。DWF(dynamic warp formation)［10］和 DWS(dynamic warp subdivision)［11］即为两种硬件机制:DWF的硬件调度器在每个时钟周期分析SIMD线程，将执行相同分支路径的SIMD道整合生成新的SIMD线程;DWS则是将SIMD线程分解为子线程，子线程被独立调度并交替执行。Zhang等［12］提出了一种在运行时重新映射SIMD线程数据的方法，由于需要昂贵的CPU-GPU数据通信，整体优化效果有限。

以上优化方案都是硬件层面的优化，虽然较为有效，但对于一般的GPU计算用户实现难度较大。因此，有必要探讨实现难度更低，可操作性更强的优化方法。本文中针对这一问题利用现有体系结构在软件层面进行优化，以期能在一定程度上优化条件分支分歧。

2 聚合优化策略的设计方案

从软件层级入手，探索提升每步SIMD执行的有效处理比重的方法，提出了利用“聚合”思想的SIMD分支优化策略，该策略针对的具体情形如下列代码所示。

由于分支条件不能在编译时确定，所以只有程序运行时才能决定线程的走向。此种情形由于GPU的执行方式使得执行某条路径时只有选择该路径的SIMD道进行实际计算，其他道被阻塞，而分支处于循环体内部导致任意时刻都有大量资源闲置。

鉴于此，聚合策略的主体思想是:在每步循环中，采用某种机制将不同SIMD道中选择相同路径的条件分支“聚合”到同一步循环中，力求提高每次循环的有效处理比重。为此，在具体实施过程中可以用不同的实现策略，本文着重对循环推迟和循环提前两种实现策略进行讨论。

2.1 基于循环推迟的聚合优化策略

循环推迟的做法是在每一步循环中，SIMD线程中的所有SIMD道只执行一条分支路径，另一条分支路径则被“挂起”，并被推迟到后续的循环中，与下一步循环合并后再择机执行。此前未执行的SIMD道与即将执行的SIMD道就“聚合”到了同一步SIMD执行中。这样做使得每次循环只执行了一条路径，另一条路径直接跳过，因此所用时间是串行执行两条分支路径的一半，从而使SIMD执行的总数少于未优化之前。

图1给出了一个SIMD线程常规分支执行与采用循环推迟策略后分支执行的两种不同情况的对比示例。其中假设SIMD线程宽度为4，循环次数为3，带下标的T和F分别代表条件判断为真(True)和为假(False)的不同路径，下标的左起第一位数代表的是在未优化的情况下第几次循环的编号，第二位数代表的是SIMD道的编号。

图1 使用基于循环推迟的聚合优化策略的示例Fig.1 A branch execution example using converging optimization strategy based on loop postpone

常规执行时，如图1(a)，每次循环内要依次将所有分支路径都执行一次，从本例来说，共有6步SIMD执行(每个循环包含两次SIMD执行)。采用了循环推迟的策略后，如(b)和(c)所示，虽然循环次数都有所增加，但是整体的SIMD执行步数却都有所减少(空路径被直接跳过，执行时间忽略不计)，最多也与未优化时相等。假设两条分支路径中的指令数目相同，则聚合后(b)情况执行的指令数降低了16.7%，(c)情况则降低了33.3%。

从上图的例子中不难看出，当遇到分支分歧时“挂起”的分支路径选择的不同，会导致最终的聚合效果不同，因此循环推迟策略的关键是在每次循环中如何选择要执行的路径。此处采用了两种较为简单的路径选择策略:多数优先策略和轮转策略。

多数优先策略是在每次分支分歧时选择包含最多SIMD道的分支路径执行，即选择执行计算单元使用率最高的路径。由于本文讨论的条件分支有两条路径，所以这样使得多数循环中SIMD执行的有效道数必然大于等于SIMD总道数的一半，如图1(b)中第0～3次循环，从而提高SIMD计算单元的使用率，减少SIMD执行的总次数，达到缩短计算时间的目的，并且整个执行过程不会破坏每个SIMD道原有的循环执行顺序。但本策略可能导致处于冷门路径的SIMD道迟迟得不到执行，如图1(b)中第2号道的第4次循环，本文中称这种现象为道饥饿。道饥饿现象的存在可能会造成最后几步循环中只有少数SIMD道执行实际操作，一定程度上限制了循环推迟的聚合效果，实际实现中可以采用周期性暂停本聚合策略来触发冷门路径的执行以缓解道饥饿现象。

轮转策略是在每次循环中遇到分支分歧时，交替的选择条件判断为真或为假的路径执行，并将另一条路径挂起和推迟到下一步循环中，从而达到聚合的效果，提高计算效率，如图1(c)所示(采用先假后真交替循环)。这样虽然在最初几次循环中聚合效果不如多数优先策略，但是每次循环中有效执行的SIMD道数却较为均等，且多数情况下超过SIMD总道数的一半，同时还避免了道饥饿现象。不足之处是如果SIMD线程的所有SIMD道在某次循环中都选择相同路径，而此时根据轮转策略恰好轮转到了另一条路径(此处称这种现象为“空载”)，会导致无用执行，实际实现中遇到上述情况要切换分支走向。

这两种策略实现起来都非常方便，可以利用CUDA本身提供的统计各SIMD道状态的函数来实现，并且所引入的开销也可忽略不计。

影响循环推迟优化效果的因素有以下4点:

(1)如果分支指令规模小于实现循环推迟的指令规模，那么其带来的收益可能不足以抵消本身的开销，甚至会导致性能损失。

(2)暂时阻塞分支同样会阻塞相关SIMD元素对循环体中后续非分支代码的执行，如若分支指令数量相比后续非分支指令较少，循环推迟可能无法带来理想的改进。

(3)分支被执行的频率、SIMD元素分支变向的频率等因素会影响循环推迟的效果。本文所采用的多数优先策略和轮转策略相对简单，其改进效果依赖具体的分支模式。

(4)循环推迟可能破坏原有的优化的内存访问模式，导致性能的下降。

2.2 基于循环提前的聚合优化策略

循环提前的做法是将原本由两次循环完成的任务“聚合”到一次循环中完成。这种策略适用于同一SIMD道执行流中第N次循环与第N+1次循环所选择的分支路径不同的情况，假设程序只有两个不同的分支路径T路径和F路径，如图2(a)和图2(c)所示，当遇到这两种情形时，可以考虑将第N+1次循环提前到第N次循环中执行，如图2(b)和图2(d)所示，从而充分利用每一次循环。

图2 基于循环提前的聚合优化策略的适用情况Fig.2 Circumstances converging optimization strategy based on loop advance targets

循环提前策略的效果依赖于原有程序路径选择的情况，图3给出了两个使用基于循环提前的聚合优化的两个示例，每个示例中SIMD线程宽度为4，循环次数为4。

示例1在使用了本策略后聚合效果达到了理想状态，如果两条分支路径中的指令数大致相当，则优化后的指令数降为原来的50%。示例2在使用了本策略后聚合效果较为一般，并非所有的相邻的循环都能使用循环提前策略，但总体性能仍然有一定提升，优化后的指令数降为原来的75%。最坏情况下SIMD线程中的某些道在整个循环过程中都只选择走同一条分支路径，本策略则在这些道上不起作用，程序受这些道拖累性能没有任何提升，还有可能下降。

图3 使用基于循环提前的聚合优化策略的两个示例Fig.3 Two branch execution examples using converging optimization strategy based on loop advance

策略的实现可以通过改造原有条件分支的执行模式，判断相邻两次循环中条件分支的路径走向，然后调整分支的执行来实现，引入的开销也不大。由于循环提前可能会调换相邻两步循环的次序，因此需要满足如下条件才能保证执行结果的正确:

(1)每步循环中各分支语句不依赖上一步循环的结果，即循环的先后次序可交换。

(2)条件分支语句内的两个不同分支之间不能出现相互依赖。

(3)循环中条件分支以后不能直接出现非分支代码。

条件(3)的原因主要是，循环提前策略合并了相邻的两步循环，从而减少了循环的次数，导致分支代码之后的非分支代码执行的次数也相应减少，无法与之前未优化的程序保持一致。如一定要有非分支代码，则可以将非分支代码整体拷贝或封装成函数后分别移入到条件分支的不同路径中。影响循环提前优化效果的因素有循环推迟中的(1)、(3)、(4)条。此外，从图3的分析也可看出，实际优化效果依赖于程序中的分支出现图2中两种情况的比例。

3 聚合优化策略的实现

从策略的设计来看，要实现聚合优化策略势必会引入新的条件分支判断，这虽然会在局部影响到程序运行的效率，但其影响十分有限。因为这些额外的条件分支当中只包含很少的代码，且多为复制和比较等简单运算，计算时间十分短暂。本文将其归结为“实现优化策略所需的指令规模”。只有当原有的分支指令规模接近或小于“实现优化策略所需的指令规模”时才可能导致性能的损失。在需要采用聚合优化策略的情况下，主要分支路径中的指令规模要远大于“实现优化策略所需的指令规模”，所以优化主要分支所带来的程序效率的提升要大于策略的开销。

3.1 基于循环推迟的聚合优化策略的实现

实现基于循环推迟的聚合策略的关键是实现两种选择路径的策略，然后根据路径选择策略的结果挂起或执行某些线程，其主体的示意性代码如下:

多数优先策略的实现可以使用线程束投票函数__ballot()和整数处理函数__popc()。__ballot()函数可以检查线程束中所有线程的断言状态并搜集至一个32位整数中，如果第n个线程的断言值与参数值相同，那么返回的整数的第n位为1。__popc()能够返回32位整数中位1的数目。使用这两个函数可以找出被多数SIMD线程执行的分支路径，进而实施多数优先策略。

轮转策略的实现方法比较直接，只需在循环中周期性地调转分支走向即可。为避免“空载”分支路径被执行的情况，可以利用线程束投票函数__all()和__any()来进行判断。如果所有SIMD线程的断言状态与参数相符，那么__all()返回非零值。如果SIMD线程中存在断言状态与参数相符的元素，那么__any()将返回非零值。利用这两个函数可以在循环出现“空载”路径时切换分支走向。

3.2 基于循环提前的聚合优化策略的实现

由于循环提前策略需要考虑相邻两步循环所选的分支路径才能决定循环是否需要提前，因此在循环体中分支语句之前需要计算出相邻两步循环中的分支条件。然后据此判明是图2中的哪种具体情况，再对不同的情况分别采用不同的提前模式，处理过程的示意性代码如下:

代码中将每次循环中条件分支中所要用到的不同的变量统称为环境变量，可以是从某处读取的数据，也可以是通过对循环变量i进行计算得到的数值等各种各样的数据，但不能是循环之间相互依赖的数据。mode用于控制优化策略模式，其取值为0、1、2。0代表无法对循环进行提前，循环按原有顺序执行。1代表图2(b)中先F路径后T路径的模式，此时需要将第N+1次循环中的T路径提前到本次进行，因此需要将循环变量以及各环境变量调整到第N+1次循环时的状态，之后再执行第N次循环中的F路径，此时又需要将循环变量和各环境变量重新调整回来，当两个路径都执行完毕之后再把循环变量递增1。2代表图2(a)中先T路径后F路径的模式，同样也需要类似的在两次循环的不同循环变量和环境变量之间进行切换。

4 试验结果及分析

试验采用的GPU加速设备是GeForce GT 550M(GF108)，拥有两颗SIMD核心，每个核心有48道，单精度峰值计算性能为284.16GFlops。软件环境是CUDA toolkit 5.0。

4.1 基于循环推迟的聚合优化策略试验

将32个SIMD线程(共32×48个CUDA线程)加载至同一SIMD核，以保证算术流水线满载，避免指令级并行变化对性能的影响。每个SIMD线程中，各道的分支走向相互独立，由 CURAND［13］库通过伪随机算法生成。每条分支路径内部包含一系列数据依赖的混合乘加(fused-multiply-add，FMA)运算，并可通过改变混合乘加运算的多少来调节分支指令－非分支指令比(核函数中，分支路径内指令数/分支路径外指令数)。试验对不同的分支指令－非分支指令比分别使用多数优先和轮转两种选路策略进行优化，并与未经优化的分支执行进行比较，得出加速比(优化前执行时间/优化后执行时间)，试验数据结果如图4所示。

从图4中可以看出，当分支指令－非分支指令比较小时，由于聚合本身所带来的开销，加速比低于1，随着分支指令规模的提升，加速比逐步提升。多数优先策略测试取得的最佳加速比为1.152，轮转策略测试取得的最佳加速比为1.256。由于多数优先策略需要定期处理道饥饿现象，所以在多数情况下加速比低于轮转策略。

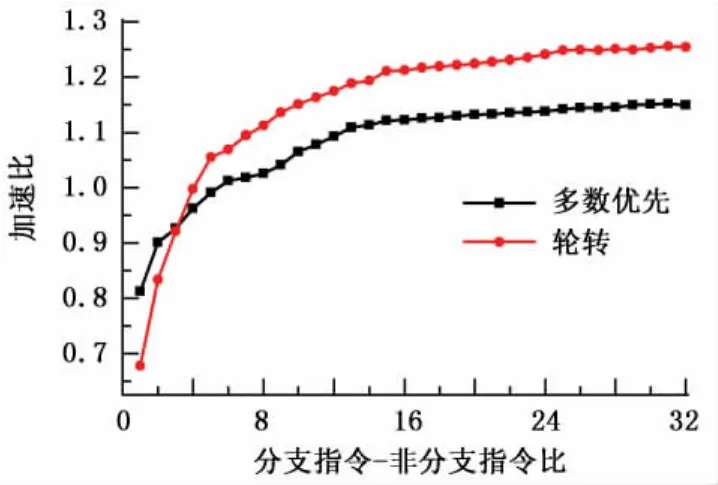
图4 基于循环推迟的聚合优化对性能的影响Fig.4 Performance impact of converging optimization strategy based on loop postpone

4.2 基于循环提前的聚合优化策略试验

加载的SIMD线程配置和分支路径内的运算与基于循环推迟的聚合优化策略相同，且同时满足基于循环提前的聚合优化策略的3个前提条件，针对条件(3)需要将循环内部原本位于条件分支语句后的非分支代码封装成函数移入条件分支内部。此处将这些函数称为非分支代码函数，并仍将其视作非分支代码。

循环提前的效果除了依赖于分支指令－非分支指令比，还依赖于循环中出现图2中两种情况的比例。此处将能够提前的循环数与循环总数的比值称为可提前比。由于同一SIMD道中每两个相邻循环都选择不同路径时也只有50%的循环可以提前，因此可提前比最大是0.5，最小是0，并且加速效果取决于可提前比最低的SIMD道。理想情况下，若只考虑分支代码，则可提前比与加速比的关系为

为更直观反应本策略的有效性，在这里用线程号threadIdx和循环变量i使所有SIMD道中的可提前比一致，试验时取了间隔相等的6个值。同时为了代表一般性，利用CURAND伪随机算法生成分支走向，试验数据结果如图5所示。

需要说明的是，图中每条曲线的前两个点的分支指令－非分支指令比是0.25和0.5，第三个点是1，以后每次递增1。在不同的可提前比情况下，随着分支代码－非分支代码比的增加，程序的加速比都在逐步提升并趋近于只有分支代码时的理想情况。当程序中可提前比过低且分支指令少于非分支指令时，本策略产生的额外开销将导致程序的加速比低于1。

图5 基于循环提前的聚合优化对性能的影响Fig.5 Performance impact of converging optimization strategy based on loop advance

5 结束语

在软件层级提出两种利用“聚合”思想的SIMD分支优化策略，将不同SIMD道中选择相同路径的条件分支“聚合”到了同一步循环中。压缩了GPU执行SIMD操作的实际次数，提高了GPU硬件在每次SIMD操作时的利用率。试验表明，在满足一定条件下能够取得较为理想的加速比，与现有的硬件层面的优化方案相比实现难度较低。本策略对分支结构有所要求，因此在一般性方面还存在不足。另外还可能存在一些影响优化效果的其他因素需进一步改进。

［1］ NVIDIA.CUDA［EB/OL］.［2013-05-12］.https://developer.nvidia.com/cuda-downloads.

［2］ NARASIMAN V，SHEBANOW M，LEE C J，et al.Improving GPU performance via large warps and two-level warp scheduling［C］//Proceedings of the 44th Annual IEEE/ACM International Symposium on Microarchitecture.New York:ACM，c2011.

［3］ DIAMOS G，ASHBAOGH B，MAIYURAN S，et al.SIMD re-convergence at thread frontiers［C］//Proceedings of the 44th Annual IEEE/ACM International Symposium on Microarchitecture.New York:ACM，c2011.

［4］ BRUNIE N，COLLANGE S，DIAMOS G.Simultaneous branch and warp interweaving for sustained GPU performance［C］//Proceedings of the 39th International Symposium on Computer Architecture.Washington:IEEE Computer Society，c2012.

［5］ FUNG W L，AAMODT T M.Thread block compaction for efficient SIMT control flow［C］Proceedings of the 17th International Symposium on High Performance Computer Architecture(HPCA).Washington:IEEE Computer Society，c2011.

［6］ NVIDIA.CUDA C Programming Guide 5.0［EB/OL］.［2013-05-12］.http://docs.nvidia.com/cuda/cuda-cprogramming-guide/index.html.

［7］ NVIDIA.NVIDIA Compute:Parallel Thread Execution ISA Version 3.0［EB/OL］.［2013-05-12］.http://docs.nvidia.com/cuda/parallel-thread-execution/index.html.

［8］ GLASKOWSKY P N.NVIDIA1s Fermi:the first complete GPU computing architecture［EB/OL］.［2013-05-12］.http://www.nvidia.com/object/fermi_architecture.html.

［9］ CUI Z，LIANG Y，RUPNOW K，et al.An accurate GPU performance model for effective control flow divergence optimization［C］//Proceedings of the 26th International Symposium on Parallel＆ Distributed Processing.Washington:IEEE Computer Society，c2012.

［10］ MENG J，TARJAN D，SKADRON K.Dynamic warp subdivision for integrated branch and memory divergence tolerance［C］//Proceedings of the 37th annual international symposium on Computer Architecture.New York:ACM，c2010.

［11］ FUNG W W L，SHAM I，YUAN G，et al.Dynamic warp formation and scheduling for efficient gpu control flow［C］//Proceedings of the 40th Annual IEEE/ACM International Symposium on Microarchitecture.Washington:IEEE Computer Society，c2007.

［12］ ZHANG E Z，JIANG Y，GUO Z，et al.Streamlining GPU applications on the fly:thread divergence elimination through runtime thread-data remapping［C］//Proceedings of the 24th ACM International Conference on Supercomputing.New York:ACM，c2010.

［13］ NVIDIA.CUDA toolkit 5.0 CURAND guide［EB/OL］.［2013-05-12］.http://docs.nvidia.com/cuda/curand/index.html