沙坡头库区三维水沙运移数值模拟研究

冯淑萍，杨 程

（1.宁夏大学研究生院，宁夏 银川 750021；2.北方民族大学土木工程学院，宁夏 银川 750021）

沙坡头水利枢纽位于宁夏回族自治区中卫市境内，在黄河干流黑山峡峡谷的出口处，距离上游拟建大柳树水利枢纽坝址12.1 km，距下游已建成的青铜峡水利枢纽122 km。沙坡头水利枢纽是以灌溉、发电为主的大型综合性工程。其控制流域面积25.34万km2，多年平均径流量为336亿m3，年平均输沙量1.6亿t，总库容0.26亿m3，灌溉面积为5.85万hm2，总装机容量为120.3 MW，年均总发电量6.06亿kW·h。沙坡头水库库区属峡谷河道型，全长14.3 km。

1 数学模型

三维水沙数学模型包括水流模块和泥沙模块。其中，水流模块采用三维非恒定流可实现的 紊流模型，泥沙模块采用全沙模型。

1.1 水流模块

水流模块在直角坐标系下的下形式为[1-2]

式中，Φ为通用变量，扩散系数ΓΦ和源项SΦ所代表的物理量如表1所示。

表1 直角坐标系下三维水沙模型通用方程中各变量在不同控制方程中的含义

表1中，u，v，w分别为x，y，z方向的Reynolds时均流速；p为时均动水压强；ρ为水的密度；t为时间；k为紊动动能；ε为紊动动能的耗散率；Gk为紊动动能产生项；v为水流的分子粘性系数；vt为涡粘性系数。参数的计算见文献[2]。

1.2 泥沙模块

泥沙模块控制方程在直角坐标系下的形式[3-5]:

（1）悬移质输沙方程

式中，Cs为泥沙浓度；ω 为泥沙沉速；εx，εy，εz分别为x，y，z向的泥沙质量扩散系数，此处取εx=εy=εz=εs，εs=v+vt/σs，σs为 Schmidt数，σs=1.0。

（2）推移质不平衡输沙方程

式中，qb、qb*分别为实际推移质输沙率和平衡推移质输沙率；Db、Eb分别为悬移质与推移质运动交界面上的泥沙下沉通量和上浮通量；qbx、qby分别为沿x和y方向的推移质输沙率；Ls为推移质不平衡输沙距离。平衡推移质输沙率由长江科学院提出的推移质输沙经验公式求得。

（3）河床变形方程

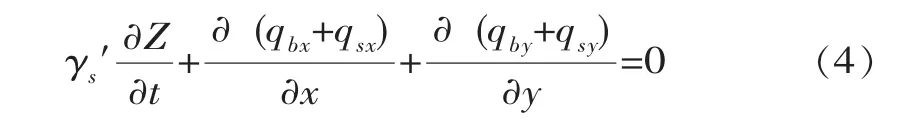
式中，γs′为泥沙干容重；Z河床高程；qsx、qsy分别为通过沿水深积分得到的沿x和y方向的悬沙通量。

2 数值计算方法

2.1 模型离散

采用格心格式的非结构网格有限体积法，对方程进行离散，采用SIMPLEC算法和TDMA算法求解。水流模块、悬移质输沙方程可统一写作

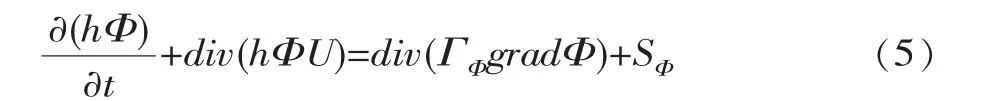
对式 （5）在控制单元上求体积分并利用高斯定理将体积分化为面积分

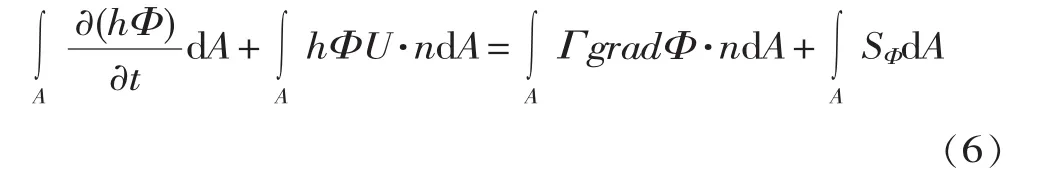
式中，U为网格单元的流速矢量；n为网格界面上的法向量。

构造辅助点对式 （6）进行离散，瞬态项采用一阶格式离散，源项采用线性化处理，具体过程可参见文献 [7]。单元面的各通量项的离散表达式及压力修正方程的离散参见文献[8]。

2.2 边界条件

两岸边界:按照无滑移处理，假定没有泥沙交换。

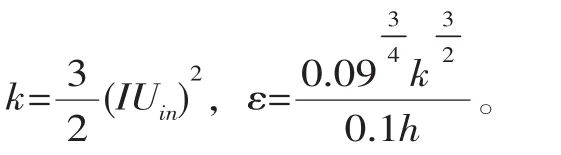
出口边界:根据实测数据，出口给定水位，各物理量在出口按照充分发展。

自由表面边界:对于水面边界采取刚盖假定，由水位变化引起的动边界，采取 “干湿边界”法来处理，假定没有泥沙交换。

3 计算实例

3.1 模拟区域及网格划分

模拟区域——沙坡头水库属于河道型水库，库区内共设置了20个断面，本文选择断面SH1～SH11共16个断面为研究对象，模拟区域、断面位置及网格划分如图1所示。本文采用Delaunay三角化法[10-11]生成三角形网格，断面SHJ4、SH6和SH5所在弯道处的网格进行了加密处理。

3.2 平面流场模拟结果分析

模拟区域的网格在纵向分为15层，选取表层（第15层）、中层 （第7层）和底层 （第1层）为例，对模拟的流场结果进行分析 （见图2）。

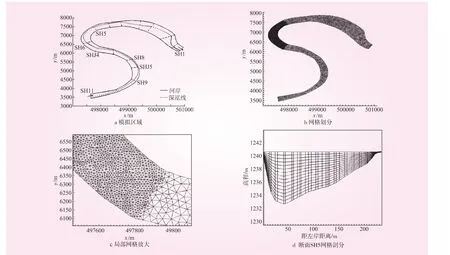
图1 沙坡头库区模拟区域及网格剖分

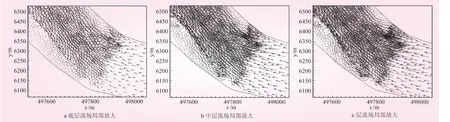
图2 沙坡头库区三层流场

由图2可知:①从底层到表层，流速逐渐增大。底层到中层的变化较为明显，中层到表层流速的增长较为缓慢。②水深位置较水浅处的流速大，中间的流速较岸边的流速大。以上两点符合水流运动的一般规律。放大图显示，稀疏的网格不能精确模拟出靠近河岸边界的流场，而网格密集的区域能精细的反映出边界附近的流场。这也说明了数值模拟中网格对模拟结果的影响很大。

3.3 断面流场模拟结果分析

以弯道处的横向断面SH6和SH5为例进行分析，3个断面流场的等速线图如图3所示。由于模拟计算的初始值2008年7月的实测值，故模拟结果中各断面是以7月份的左岸水边点作为原点，而实测结果是2008年12月实测值，两次实测时同一断面的水面宽度稍有不同，故图3中部分断面模拟结果与实测结果的横坐标稍有差异。

以断面SHJ4为例，将模拟计算的断面4等分，即得3条垂直于河面的垂线，每条线上取5个点，将断面的流速的模拟值与实测值进行对比，如表2所示。其中，y1，y2，y3为从左岸起三条垂线，表2中对应的为垂线上点的高程值，y1，y2，y3距左岸分别为:65、130、195 m；u1为模拟值；u2为实测值。

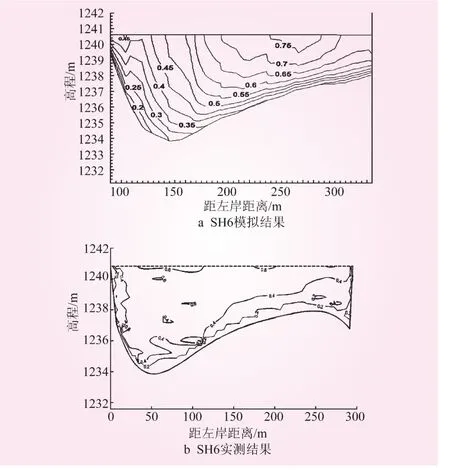
图3 沙坡头库区部分横向断面等流线

由图3和表2可知:①模拟结果与实测结果较为一致，表明本文建立的三维水沙模型中的水流模块是适合对库区进行模拟计算的；②从河底到河面流速逐渐增大，符合水流运动的基本规律；③结合图1中深泓线的位置，几个断面的最大流速与深泓线均匀不同程度的偏移，其中SH6和SH5偏移较多。由此可知，一般而言，最大水深处流速一般最大，但是在弯道的拐点、进出口、突扩或突缩等流场变化剧烈处主流与深泓线分离。

3.4 断面垂向平均流速、主流与二次流的比较

通过上述3.2、3.3两个部分的分析，说明流场的模拟结果符合水流运动的一般规律，并与实测结果较为一致。为了进一步验证模拟结果与实测结果的一致性，下面以断面SH5的主流和二次流的模拟值与实测值进行比对、分析。

将模拟计算中的断面5等分，即得4条垂直于河面的垂线，然后将垂线上的模拟值与对应位置的实测值进行比较、分析 （见图4）。断面SH5的4条垂线距左岸的距离分别为47、94、141、188 m。

由图4可知，第一，模拟值与实测值较为接近，且主流流速沿垂线的分布均符合对数律；第二，离河床床面越远，主流流速在垂向的变化逐渐减小；第三，断面的都是靠近水面处的横向流速为负，靠近床面的横向流速为正。

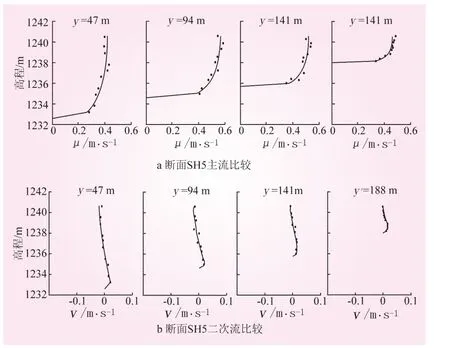
图4 断面主流、二次流比较 （定义从左岸指向右岸为正）

3.5 河床变形模拟结果分析

在二维水沙运移模拟中已对部分断面的河床变形进行了比对。这里选择断面SH7和SHJ4进行简要分析。4个断面的河床高程对比如图5所示。

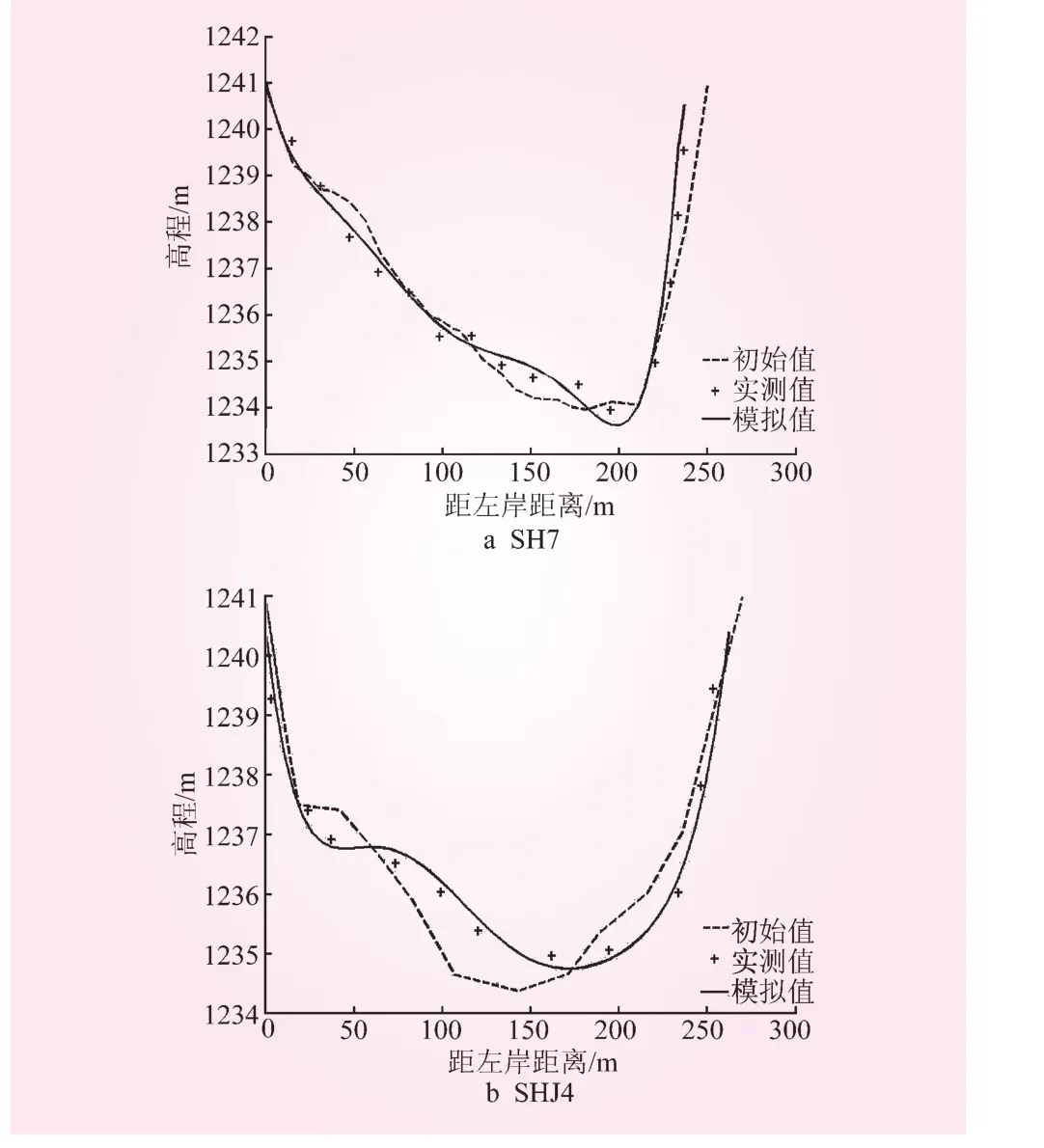
图5 沙坡头库区部分断面河床高程对比

由图5可知，模拟值与实测值较为一致，表明本文建立的三维水沙模型中的泥沙模块能应用于沙坡头库区河床变形的模拟中。

4 结 语

以沙坡头库区断面SH1-SH11段为研究对象，利用三维水沙紊流模型，采用非结构网格有限体积法、压力修正算法，对库区三维水沙运移进行数值模拟。对库区三个典型层面的流场以及断面流速分布、主流、二次流及河床高程的模拟值与实测值进行的对比、分析结果表明，两者较为一致。得到以下结论:①从库区底部到表层流速逐渐增大；②水深处流速一般较大；③弯道的拐点、突扩及进出口等流速变化距离的地方主流与深泓线出现分离现象；④主流流速沿垂线的分布均符合对数律；⑤离河床床面越远，主流流速在垂向的变化逐渐减小。这些验证了模型的准确性，及非结构网格有限体积法的适用性。

［1］陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.

［2］景何仿,李春光.黄河上游连续弯道水流运动及泥沙运移数值模拟研究[M].郑州:黄河水利出版社,2012.

［3］假冬冬,邵学军,王虹,等.荆江典型河湾河势变化三维数值模型[J].水利学报,2010,41（12）:1451-1460.

［4］CANICO L,NEVES R.Three-dimensional model system for baroclinic estuarine dynamics and suspended sediment transport in a mesotidal estuary[C]//2nd International conference on Computer Modelling of Seas and Coastal Regions,Computational Mechanics Publications,1995,353-360.

［5］陈国祥,陈界仁,沙捞·巴里.三维泥沙数学模型的研究进展[J].水利水电科技进展，1998，18（1）: 13-19.

［6］唐日长.泥沙研究[M].北京:水利水电出版社，1990.

［7］LAI X J，WANG D G，CHEN Y.Pressure correction method on unstructured Grids[J].Hydrodynamics,2004,16（3）: 316-324.

［8］赖锡军，汪德貜，傅源方.非结构同位网格SIMPLE类算法收敛性能比较[J].空气动力学报，2004，22（3）: 289-294.

［9］KANG H,CHOI S U.Reynolds stress modeling of rectangular open-channel flow[J].International Journal for Numerical Methods in Fluids,2006,51（11）: 1319-1334.

［10］陶文铨.传热与流动问题的多尺度数值模拟:方法与应用[M].北京:科学出版社,2009.

［11］陶文铨.计算传热学的近代进展[M].北京:科学出版社,2001.