让抽象变形象,让难点“动”起来
师家庆
(陕西师大附中,陕西 西安 710000)
纵观历年高考,以洛伦兹力为背景,考察带电粒子在磁场中运动问题的试题非常多,且多为综合性,中高难度,亦即我们平常所说的“压轴题”,相应分值也在20分左右,其在高考中的重要程度不言而喻.但洛伦兹力问题对于大多数学生来说又是一个困难,难点之一,就是带电粒子轨迹的确定.主要体现在动态过程过于抽象,临界条件难以寻找.下面笔者将根据课堂中的切实体会,将几何画板处理此类问题的方法和优点作以介绍.
1 几何画板处理带电粒子运动轨迹(后称轨迹圆)的缩放问题
轨迹圆缩放,是指带电粒子进入磁场后时,入射速度方向确定,大小不确定的一类问题.因为速度大小不确定,由洛伦兹力公式f=qvB及向心力公式f=可知,轨迹圆半径此为带电粒子运动的限定条件.若给磁场加上边界,即成为一临界问题,例题如下.
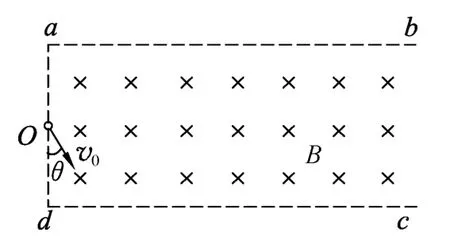
图1
例1.如图1所示,一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场,在ad边中点O,方向垂直磁场向里射入一速度方向跟ad边夹角θ=30°、大小为v0的带正电粒子,已知粒子质量为m,电荷量为q,ad边长为L,ab边足够长,粒子重力不计,求:(1)粒子能从ab边上射出磁场的v0大小范围.(2)粒子在满足(1)中条件时,在磁场中运动的最大时间.此问题的常规分析过程我们在此不再赘述,下面分析几何画板在分析该问题时所带来的方便.
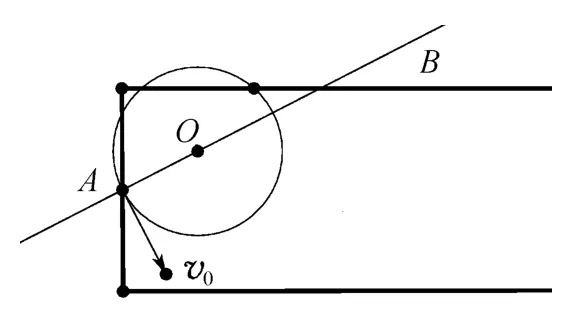
图2
(1)我们先利用几何画板画出以边界磁场以及初速度所决定的轨迹圆如图2.
选定A点与v0线段,构造垂线,则可得直线AB.根据洛伦兹力及带电粒子在磁场中运动相关知识可知,轨迹圆的圆心必然在直线AB上.建立点O,依次选定点O与点A(注意顺序),以圆心与过圆心上的点构造圆,则可得轨迹圆如图2.点O可顺直线AB任意拖动.
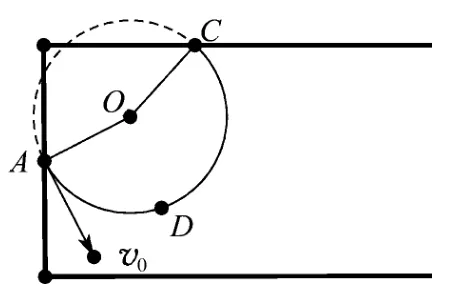
图3
(2)找出从上边界出磁场的临界条件.
在圆上建立点D,并找出轨迹圆与磁场上边界的交点C,依次选择A、D、C3个点,点击过3点的弧,即在图中形成该段弧即为粒子在磁场中运动的轨迹,其所对应圆心角为粒子运动所转过的角度,时间与该角度成正比.当拖动圆心O时,半径发生变化,对应弧长度也发生变化.
当初速度减小直至OC与上边界垂直时,达到临界条件.若初速度再减小,粒子将从左侧射出,如图4.此时,几何画板中动态图像中的C点将会消失,在到达临界条件前所对应的圆心角增大,运动时间增长.
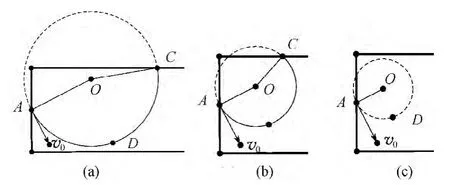
图4
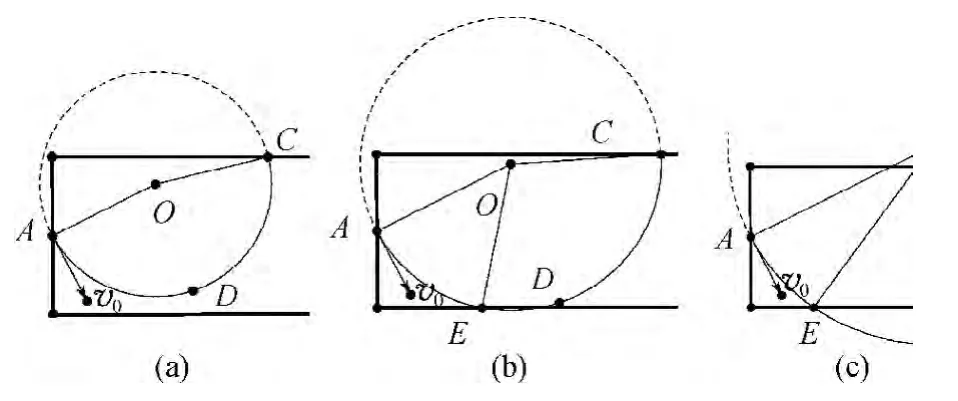
图5
当然,为了更好地体现整个动态过程,可让点O形成动画,并追踪,不同初速度粒子轨迹将动态反应并记录下来,作以比较,能够更清晰地获得临界条件,如图6.
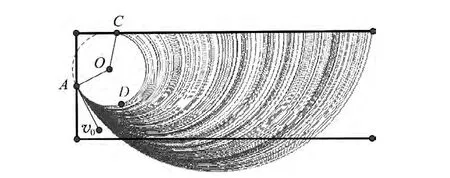
图6
2 几何画板处理轨迹圆的旋转问题
轨迹圆旋转,是指带电粒子进入磁场后时,入射速度大小确定,但方向不确定的一类问题.因速度大小确定,所以轨迹圆半径恒定,但因为速度方向不确定,所以轨迹圆位置不确定,在此过程中,粒子所有可能出现的区域构成一个以定点——粒子入射点——为圆心,以轨迹圆直径为半径的大圆,如图7(几何画板描绘).其中,图像中央较粗线为轨迹圆圆心的可能位置.

图7
例2.如图8,水平放置的平板MN上方有方向垂直于纸面向里的匀强磁场,磁感应强度为B,许多质量为m,带电荷量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域,不计重力,不计粒子间的相互影响.下列图9中阴影部分表示带电粒子可能经过的区域,其中R=mv/qB,哪个图是正确的?
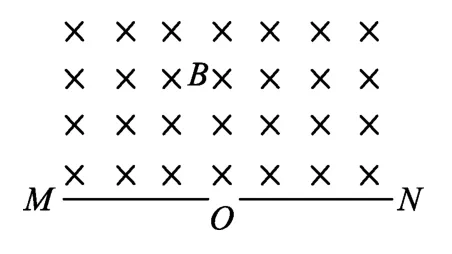
图8
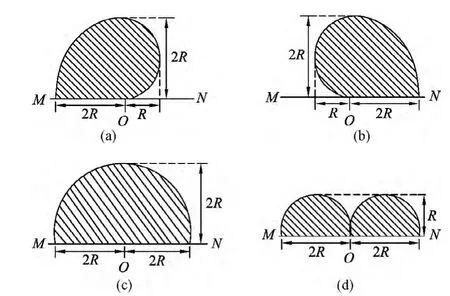
图9
解析:本题几何图像用常规方法画图很难让学生彻底明白,我们下面分析几何画板如何处理这个问题.
(1)假设整个空间存在磁场,则粒子的运动区域即为一个简单的轨迹圆旋转问题.我们先构造圆心可能经过的位置,如图10,图中点O′所在圆即为轨迹圆圆心可能经过的位置.而以O′为圆心的圆即为轨迹圆.为避免O′所在圆对我们造成影响,可隐藏该圆,如图11.
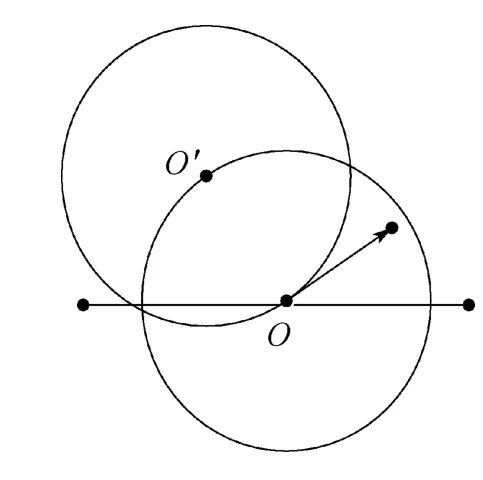
图10
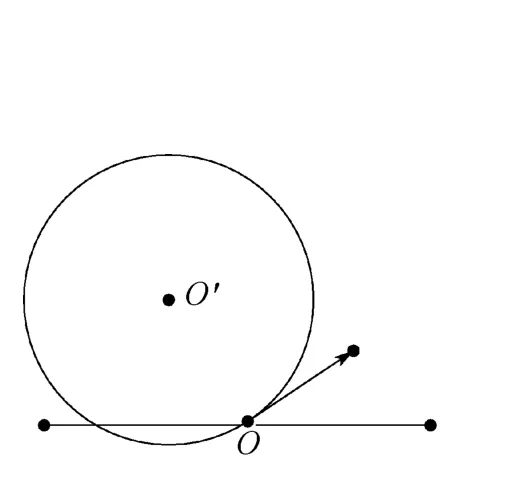
图11
(2)让轨迹圆旋转,并让表示入射速度v的箭头随之一起旋转,追踪轨迹圆,则形成如图12的图形.
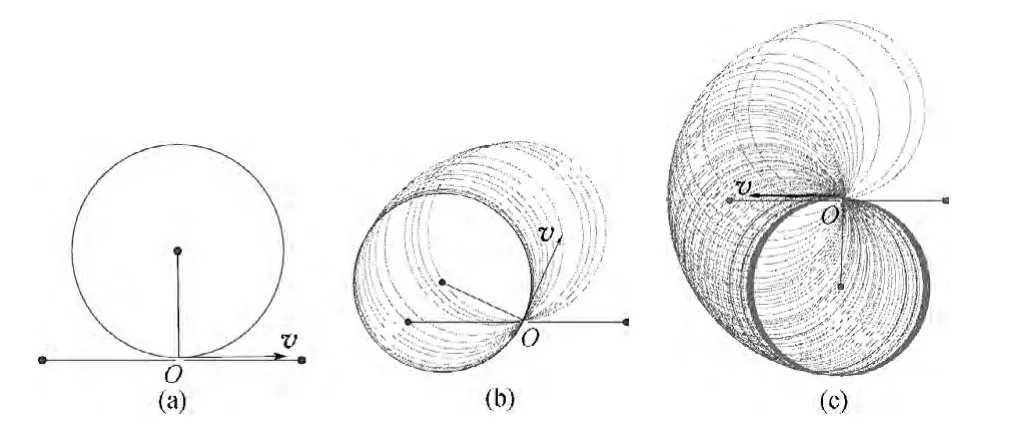
图12
因下方区域不存在磁场,所以我们只研究从初速向右至初速向左的过程.同时因为平板MN对粒子的阻碍,所以只取平板上方的区域,综合以上条件,可得结果如图13所示,即可得到正确结果.
从以上两例可以看出,利用几何画板可以更好地将带电粒子在磁场中的运动过程动态地演示出来,让学生更直观地观察带电粒子在条件约束下的运动,将抽象问题形象化,将学生难以理解的过程以动态的形式显现出来.通过几何画板,可以很好地将教师从繁复的绘图与语言讲解中解脱出来,也为学生学习此类问题积累了一定的经验模型.

图13

