为什么发射速度越大线速度越小
朱具德 徐虎勤
(江苏省新沂市第一中学,江苏 新沂 221400)
1 问题的提出
对于卫星(本文指的均是圆轨道卫星)其发射速度越大,稳定时其轨道离地面就越高,轨道半径就越大,根据
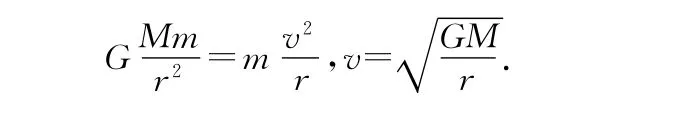
即线速度就越小.但为什么发射速度越大,轨道越高,线速度越小?这可从两个方面分析.
2 问题的分析
(1)利用引力势能公式.
设地球质量为M,半径为R,卫星质量为m,距地面高度为h,G为引力常量.取距地球球心无穷远处引力势能为0,则卫星在轨道上的势能为
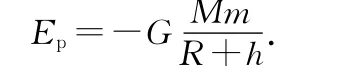
不计空气阻力,根据机械能守恒定律有
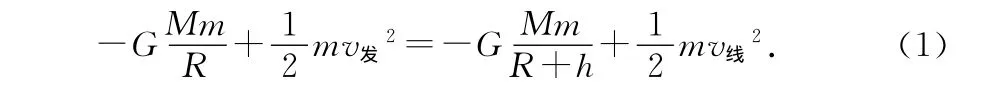
卫星做匀速圆周运动时有

由(1)、(2)式可得
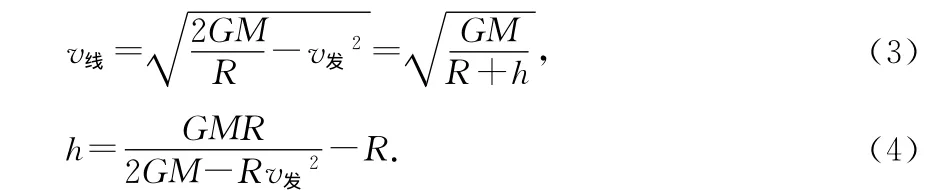
由(3)、(4)式可见,卫星发射速度越大,轨道越高,线速度越小.
由此也可看出发射高轨道卫星比发射低轨道卫星更为困难,从能量的角度来讲:一方面考虑空气阻力时,高度越大,火箭需要克服阻力做功越多;另一方面高度越大,火箭需要克服地球引力做的功也越多.
上述方法尽管严密,但是由于中学阶段并未学习引力势能公式,所以笔者再尝试运用离心现象理论进行分析.
(2)利用离心现象理论.
假设卫星贴着地面上的A点沿切线被发射出去(如图1),发射速度为第一宇宙速度v1=7.9km/s,则万有引力刚好提供卫星所需向心力,即

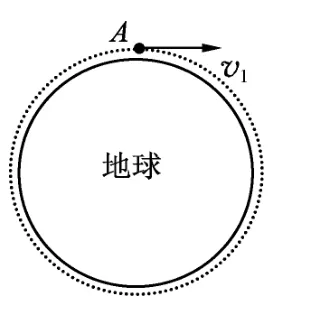
图1
此时卫星正好做匀速圆周运动,且v发=v线=v1.
如果卫星以较大的发射速度v2(比如v2=9km/s)发射,由于地球对卫星提供的引力小于卫星所需的向心力,即它将做离心运动,绕地球运行的轨迹就不是圆,而是椭圆.要想使它的轨迹是圆,怎么办?

显然不能任其自由飞行,而应在卫星飞行到距地面某一适当高度位置(设为B点,高度为hB)改变飞行方向.因为卫星在初始离心飞行阶段有

随着卫星飞离地面越远越高(h增大),其速度v2′逐渐减小,此时地球提供的引力和卫星所需的向心力虽然都在减小,但是卫星所需的向心力减小更快.根据
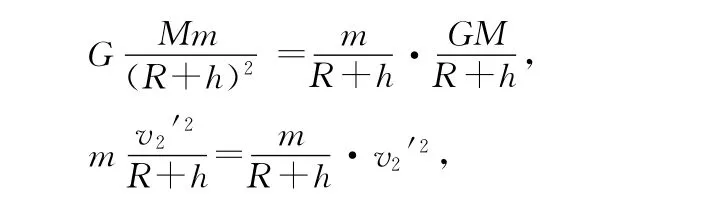

这时,改变卫星飞行方向如图2,其飞行的轨迹就是圆了.
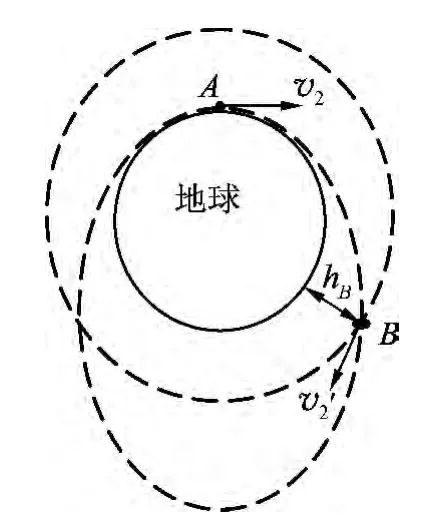
图2
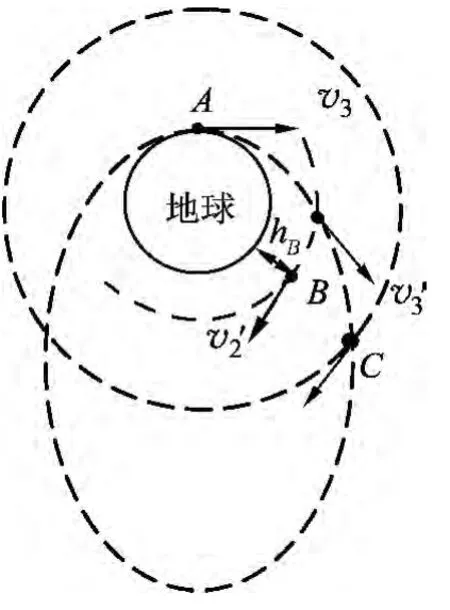
图3
如果卫星的发射速度更大为v3(如v3=10km/s),它飞行到刚才B位置所在的高度(设速度为v3′)改变飞行方向就不行了.因为v3>v2,所以v3′>v2′.卫星仍离心.
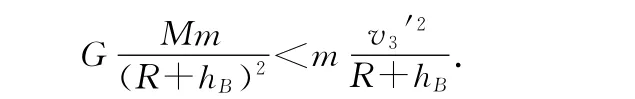
仿上,卫星应在离比B更高的某一恰当位置(设为C)改变飞行方向才能使其轨迹变为圆,如图3所示,其线速度更小.综上,卫星发射速度越大,轨道越高,线速度越小.
3 结束语
以上只是为了分析问题方便而给出的卫星发射简化模型.事实上卫星的发射并不像炮弹发射那样一蹴而就,其发射速度是逐渐增大的,其飞行轨迹由椭圆变为圆也是极为复杂地加以控制的.
——《势能》

