小波基预测函数控制在陶瓷烧成温度控制中的应用*

侯 宁 费树岷

(1 江苏开放大学 江苏 无锡 214011)(2 东南大学自动化学院 南京 210096)

陶瓷烧成窑炉是陶瓷生产过程最主要的设备，是生产过程的“心脏”，对提高陶瓷产品的品质起着决定性的作用。但是由于陶瓷烧成窑炉具有大纯滞后的特征，并且控制关系具有非线性，系统与控制指标(如温度，气氛，压力)之间为较强耦合，又表现为不确定性，普通的控制策略很难对其实现有效控制。为此一些针对陶瓷烧成窑炉控制策略被提出，文献[1]提出变结构温度控制方法，即通过模糊控制和时间比例分割相结合应用于陶瓷烧成窑炉中，并证明控制方法是有效的；文献[2～4]将智能控制与PID控制技术相融合，通过整合两种控制思想形成了模糊PID控制器的设计方法，对窑炉各工作区的温度的调节是可行的；文献[5]通过模糊控制和预测控制2种策略的结合来控制烧成温度，在精度和快速性方面取得较好的效果。文献[6]通过RBF神经网络建立对窑炉的温度特性进行建模，解决了用普通控制算法建立非线性对象精确模型的问题，并结合动态矩阵预测控制实现对温度变化的跟踪控制；文献[7]将窑炉内的温度偏差及偏差变化率通过智能逻辑控制器得到控制信号，实现烧成温度的智能控制。

预测函数控制(Predictive Functional Control, 简称PFC)是第三代模型预测控制算法，由J Richalet于1986年提出[8]，广泛应用于机器人跟踪、雷达跟踪、热焓控制等领域[9～14]。该方法的特点是在控制量的结构中加入了基函数的内容，基函数的形式以及数量可以根据控制过程预先选定，控制量的解析解为与基函数相关的线性组合，各基函数作用系统形成的输出为加权组合结构，通过目标函数的优化得到加权系数。在普通PFC控制方法中，基函数一般可取阶跃函数、斜坡函数、指数函数以及正弦多项式函数等。这类基函数结构简单，离线计算方便，不足的是以上函数都是全局函数，对信号的逼近不能根据信号的局部特征即不同逼近精度而灵活设置，难以达到预期的控制效果[15]。笔者提出一种基于小波基函数的陶瓷烧成窑温度预测函数控制方法，仿真结果表明该方法的有效性。

1 陶瓷烧成窑炉温度预测函数控制

根据控制系统的要求，对陶瓷烧成温度进行控制，要求控制过程输出即烧成温度能够快、准、稳地达到设定温度值。

1.1 陶瓷烧成窑炉数学模型[16]

为了获得陶瓷烧成窑炉数学模型，可以从数学途径分析其工艺过程,写出有关的数学关系表达式,然后推导出被控对象的模型。作为具有代表性的生产过程,陶瓷烧成窑炉模型可表示为以下常见工业过程：

(1)

式中：K——比例常数;

τ——时延时间；

T——过程时间常数。

式(1)表示的是一阶惯性加纯滞后模型。当式中τ与T的比值大于0.3时，称为大纯滞后惯性环节；当比值小于0.3时，称为一般纯滞后惯性环节。笔者在对象数学模型的仿真过程中取K=5，τ=10，T=20，即大纯滞后惯性环节。

1.2 控制输入与模型输出

预测函数控制方法在控制量的结构中加入了基函数的内容，控制量为：

(2)

式中：μj——线性组合的加权系数;

fbj(i)——基函数在t=iT时的取值;

nB——基函数的个数;

h——预测优化时域的长度。

陶瓷烧成温度预测函数控制的模型输出ym(k+i)可以表示为：

ym(k+i)=yU(k+i)+yF(k+i)

(3)

式中：yU——自由(unforced)响应输出，即为输入控制为零情况下模型的响应;

yF——由式(2)所给的新增控制输入作用下的强迫响应，可以由下式得到：

(4)

式中：ybj(i)为过程在第j个基函数fbj(i)作用下的模型输出，不需要在线计算出；加权系数μj(k)可以通过在线求解得到。

陶瓷烧成温度预测函数控制的预测模型为：

Xm(k)=EmXm(k-1)+Fmu(k-1)

ym(k)=CmXm(k)

(5)

式中：Xm∈Rn*1——状态向量；

u∈R1*1——控制输入；

ym∈R1*1——预测模型输出；

Em∈Rn*n、Fm∈Rn*1、Cm∈R1*n——分别是模型的系数或向量。

由式(2)、(3)、(4)、(5)得到：

ym(k+1)=CmXm(k+i)

(6)

式中:μ(k)=[μ1(k),μ2(k),L,μnB(k)]T;

yb(i)=[yb1(k),yb2(k),L,ybnB(k)]T。

1.3 控制系统参考轨迹

为了达到预期的控制目标，系统的模型输出在控制过程中要能跟踪参考轨迹，从而使系统控制温度能够平稳的达到预期温度值(设定值)。预测函数控制的参考轨迹在形式上没有特别限制，笔者选取以下指数形式作为过程跟踪参考轨迹，其表达式为：

(7)

式中：yR(k+1)——k+i时刻参考轨迹的值；

s(k)——设定温度值轨迹；

yp——实际过程输出；

sb(k)——多项式系数；

Bs——表示多项式阶数。

1.4 误差补偿与优化计算

对于过程输出与模型输出之间的误差问题，通过反馈进行未来误差的预测和补偿，通常取未来误差为：

(8)

式中：et(k)和Be分别为多项式的系数和阶数。

(9)

预测函数控制方法中控制量是通过优化实现的。具体做法是在预测时域上取若干优化点，使得优化目标函数表达式为：

(10)

式中：nh——拟合点的个数，且nh≥nB；

hj——第j个拟合点的值，即为介于优化时域之间的一些离散点。求 ∂J/∂μ(k)=0,求解出[μ1(k),μ2(k)，KμnB(k)]后，通过式(2)可得到控制量的解析式。

针对式(1)所示的一阶惯性加纯滞后系统,在τ=0模型上进行修正，思路如下：

ypa(k)=ym(k)+yp(k)-ym(k+D)

(11)

设跟踪预期温度值为阶跃设定值，则s(k+i)=s(k)，经优化计算可得到k时刻的控制量：

(12)

式中各系数：

式中：A=(GGT)-1G;

G=[yb(h1),yb(h2),K,yb(hnh];

yb(i)=[yb1(k),yb2(k),K,ybnB(k);

fb(0)=[fb1(0),fb2(0),L,fbnB(0)]T。

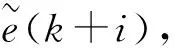
1.5 小波基函数的选择

根据预测函数控制的方法，系统的控制精度取决于基函数的选取[17]，而基函数的选取则依赖设定值以及控制对象的性质。基函数选得越少越简单，需优化计算的加权系数也就越少，算法的快速性可以提高，但控制精度将降低。在普通的预测函数控制研究中，大多选取阶跃函数、斜坡函数、指数函数以及正弦多项式函数[18]作为PFC的基函数，由于这些函数是全局函数，对参考轨迹的逼近不能随预测时域的递增作灵活的调整，为了解决这一不足，考虑选择某种具有紧支撑局部特征且在布局上能灵活设置的函数作基函数。

fbj(i)=B(i,j)

(13)

nB——基函数的个数；

nh——拟合点个数。

选择Mexican Hat(Mexh)小波基作为陶瓷烧成窑炉温度PFC的基函数。该小波基是Gauss函数的二阶导数，在时域和频域都具有很好的局部化特征，小波基系数衰减很快。其表达式为：

(14)

小波基函数的选取方法是:在预测时刻较小时段对参考轨迹逼近要求较高，为了满足一定的精度要求可以设置以多个细尺度的小波基函数逼近；随着预测时刻的增大，对参考轨迹逼近要求逐渐降低，则以少量粗尺度的小波基函数逼近，尽量减少基函数的个数。图1和图2为不同设置的小波基函数分布图。

图1 Mexican Hat(Mexh)小波基函数不均匀分布

Fig.1 Uneven distribution of Mexican Hat(Mexh )Wavelet basis function

图2 5个小波基函数均匀分布Fig.2 Even distribution of 5 Wavelet basis functions

图1利用小波基的多尺度特性，灵活选取了3个不均匀分布小波基函数。在逼近精度较高处设置了2个细尺度的小波基函数；随着预测时刻增大，在精度要求相对降低处设置了一个粗尺度的小波基函数，在满足一定精度要求的同时减少基函数的个数，提高算法的快速性。图2为在预测时域内设置的5个均匀分布小波基函数。

利用小波基函数PFC方法另外还有一个特点就是由于小波基函数是紧支局部函数，因此在式(12)表示的当前控制量u(k)时只需计算第一个小波基函数fb1(0)的权系数μ1，并不需要计算所有的权系数，因此快速性得到了进一步的提高。

2 陶瓷烧成窑炉闭环系统性能分析 [19]

假设被控对象的实际模型为：

(15)

陶瓷烧成窑炉模型为常见一阶系统，因此式(15)中的系数矩阵都是1×1维矩阵。当跟踪设定值为阶跃变化，由式(12)得到PFC的控制作用为：

u(k)=no(s(k)-yp(k))+nmXm(k)

(16)

考虑系统外部干扰，令：

y(k)=yp(k)+d(k)

(17)

式中：d(k)——外部扰动;

y(k)——系统的实际输出。

由式(5)、(15)、(16)、(17)得出陶瓷烧成温控闭环系统的输出y(z)方程：

y(z)=yp(z)+d(z)

(18)

由上式得到传递函数：

(19)

(20)

式中:n0=fb1(0)yb1(h1)-1(1-αh1)

当模型匹配时，可得到

(21)

(22)

式(21)、(22)表明，预测函数控制能够对阶跃设定值实现无偏差跟踪，理论上无稳态误差，并且完全能够抑制外部干扰，因此具有较强的鲁棒性。

由式(18)还可以得到温度控制闭环系统的特征方程为：

1-nm(zI-Em)-1Fm+n0C(zI-E)-1F=0

(23)

其特征根为：

(24)

由式(7)和(10)可得出:0<α<1,h1>1。01。因此上式特征根0

3 仿真比较

笔者选取纯滞后一阶惯性环节为陶瓷烧成温度控制仿真对象：

其中参数取K=5,τ=10,T=20。该模型同时也作为小波基函数PFC的预测模型，并且在仿真过程中预测模型都不改变。

3.1 选取不均匀分布基函数

选取如图1所示的3个不同预测时刻不均匀分布的小波基函数。在预测时刻较小且逼近要求较高时(p=0,15)选取细尺度(a=10)的Mexh小波；而在预测时刻较大时(p=50)选取粗尺度(a=20)的Mexh小波进行逼近。

图3 跟踪阶跃设定值时的仿真结果比较Fig.3 Tracking the simulation results when the step setpoint

3.2 选取均匀分布基函数

选取5个均匀小波基函数，其不同预测时刻的均匀分布如图2所示。仿真参数不变。同时对图1、图2所示2种不同分布的小波基函数情况进行仿真，并进行比较，结果如图4所示。

图4 不同分布的小波基函数的仿真结果比较

Fig.4 Simulation results of the different distribution of the wavelet basis function

由图4可知，不均匀分布的即具有申缩特性的小波基函数的动态特性要比均匀分布的小波基函数更好些，可见在保证一定精度的前提下，选定不均匀分布的小波基函数，减少了基函数个数，优化了待求变量的个数，提高了系统的整体控制效果。

3.3 受干扰情况

为说明基于小波基函数PFC的抗干扰能力,在系统进入稳定时间 200 s处，加入20% 干扰信号后的响应曲线如图5所示。仿真结果表明，加入干扰后，小波基函数PFC的温度回到设定值的时间比普通PFC要快5～8 s。可见抑制干扰的能力优于普通PFC。

4 结语

笔者利用小波基函数的紧支局部性、多尺度分析特性等特征，针对普通PFC方法中基函数的选取存在的不足，提出基于小波基函数的陶瓷烧成窑温度预测函数控制方法。通过不同情况的仿真比较，表明小波PFC算法在顾及优化目标整体性的同时，又满足了在不同预测时刻对参考轨迹逼近的精度要求，实现了基函数的个数和分布根据不同要求的灵活设置。该方法算法简单,易于实现,在响应速度、控制精度、抑制外部干扰等方面比普通PFC方法都有明显的改善，具有良好的应用前景。