对输送系统影响的泥浆性能研究*

康建喜 王荣杰

(咸阳陶瓷研究设计院 陕西 咸阳 712000)

前言

固体粒状物料与液体的混合物称为浆体。浆体根据液相的不同可分为：液相是水的称为水系泥浆和液相是水以外的其他的液体的称为非水系泥浆两种。

水系泥浆在实用领域内占有很大比例，作为大宗物料输送的有煤浆，矿浆，水泥生料浆(石灰石浆)，化工磷灰石浆，城市污泥浆和工业废渣(电厂灰渣浆，矿山尾矿浆)等。

研究泥浆的性能对输送系统具有非常重大的意义；对于输送系统泵型的选择，管道的选择，输送系统的经济投资，输送系统运行的成本，输送系统功率的选择等方面具有非常重要的意义。

1 泥浆的分类

按照流动性的差别，泥浆可分为均质体，非均质体，伪均质体的带滑移沉积层的泥浆，有固定沉积层的泥浆等。

1.1 均质体

在均质体当中，固体颗粒在300～400目，颗粒非常小。在流速较低或静止的情况下，泥浆不会发生沉淀或分层，为均匀状态的悬浮液。 这类泥浆为牛顿流体性状，但大多为非牛顿流体性状，一般把它们按照宾汉体或伪塑体来研究。均质体在管道输送当中，按照非沉淀性的浆体来对待。

1.2 伪均质体

在泥浆当中，其中的固体颗粒比较大或者固体颗粒的容重比较大，只有保持一定的流速才能使泥浆上下的固含量变化不大，这类泥浆叫做伪均质体，只有保持一定的流速才能变成均质体。

1.3 非均质体

在泥浆当中的固体颗粒直径大于0.05 mm时，或者容重较大时，即使有一定的流速泥浆中上下固含量差别也非常大。只有随着流速的增大才能改善其状况，当流速达到一定时非均质体可变成伪均质体。

对于某种特定的浆体，都有一个沉淀流速，当管道的流速低于沉淀流速时，在管道的底部就会有一层跳跃或者滑动的固体底层，称做滑移层非均质体。当流速低于沉淀流速时，这层固体底层就会沉淀下来，这个时候的这个状态就称做固定沉积层非均质体。非均质体属于固液两相流动状态，其研究方法按照固液两相流的方法来研究。非均质体的研究方法按照沉降性泥浆来研究。

2 粒料及泥浆的物理性能研究

粒料及泥浆的物理性质有粒料容重，粒径及其分布，颗粒形状系数，颗粒沉降阻力系数和沉降末速，泥浆浓度和最大沉降浓度，粘度或刚度系数，初始切应力，泥浆比热和导热系数以及磨蚀率和磨蚀米勒数等。

2.1 固体物料容重

单位体积粒料的质量称为粒料的容重，常以γg表示，单位为t/m3或kg/m3。

常用泥浆输送各种粒料的容重见表1。

表1 各种粒料的容重

2.2 粒径及其分布

粒径是指该种粒料通过某种筛孔和不能通过的下一级筛孔的平均值，以d表示，单位为mm。

实用的筛孔标准有泰勒筛和国际标准筛。对于工程实际情况，粒料是不均匀的，较为常见的是粒径在一个按指数函数分布的范围内变化。为了表征这种大小不均匀的颗粒粒径特征，常用所谓特性粒径来表示。

表2 粒料允许上限粒径

最常用的特征粒径有加权平均粒径，中值粒径 (小于该粒径所占质量为50%)，上限粒径 (小于该粒径所占质量为95%)等。

dp=∑di·Δpi/∑Δpi

式中：di——某级粒径值；

Δpi——该级粒径所占质量百分数。

常用于泥浆输送的粒料允许的上限粒径见表2。

2.3 颗粒沉降阻力系数和沉降末速

2.3.1 颗粒沉降阻力系数

固体颗粒在粘性液体中与其作相对运动时，由于固液边界上流速梯度的存在，使液体对固体边界产生剪切力，也就是产生阻力。对于不同颗粒的大小和不同流体运动的特性，这种外流阻力在颗粒沉降过程中用沉降阻力系数CD来表示。

在紊流状态下，即雷诺数1 000≤Re≤2×105时:CD=0.4。

在过渡状态下，即雷诺数1≤Re≤1 000时：

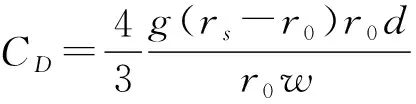
式中:W——颗粒沉降末速,m/s；

μ——液体(水)的粘度；

rs,r0——颗粒和水的容重,t/m3、kg/m3；

d——粒径,m；

g——重力加速度。

2.3.2 沉降末速

颗粒在液体中在重力条件下达到的最终沉降速度称沉降末速，其通用计算式为：

上式是隐函数形式，计算时要试算，逐步逼近求解。为了简化计算，给出了近似计算的显函数式，其在常用的0.05≤Re≤20区域内为：

式中r为水的粘度；其余符号同前。

2.4 泥浆浓度和最大沉降浓度

2.4.1 泥浆浓度

泥浆浓度有几种表示方式：体积浓度Cv为泥浆的固体体积Qs和泥浆体积Qm之比。质量浓度Cw为泥浆的固体质量Qsrs和泥浆体积Qm之比。

2.4.2 最大沉降浓度

对一种特定的泥浆而言，其固含量在由小变大的过程中，泥浆始终未流动，当固含量最大时，泥浆开始沉淀，这个时候的体积浓度叫做最大沉降浓度或沉降时候的极限浓度。其符号为Cmv。这个数值为泥浆输送前需要浓缩到的最大浓度值。对于泥沙，经验计算公式为：

Cmv=0.755+0.222logd50

对于金属砂浆，经验公式为：

以上两式中d50和dp分别为中值粒径和加权平均粒径，其他符号同前。

通常情况下最大沉降浓度应根据试验确定。

2.5 粘度和刚度系数

流体各个相邻部分以不同速度流载时，在使速度成为“均一”的方向上会出现剪切应力，这种性质称为液体的粘性，度量这种粘性称为粘度。

泥浆的粘度比单一液体(如水)的粘度大，对于体积浓度较小的由较粗的刚性小球组成的稀泥浆，呈现牛顿流体的性状。当浓度增加而固体颗粒甚小时，则会呈现非牛顿流体性状。

式中μ为液体的动力粘度。

泥浆动力粘度μm与水的动力粘度μ0之比称为相对粘度，它是泥浆体积浓度(Cv)的函数。

对于非牛顿流体，特别是常见的宾汉体τ为：

式中η为刚度系数。

对一般泥浆而言，刚度系数与泥浆的体积浓度、泥浆当中的颗粒大小、泥浆的温度都有函数关系。同样，相对刚度系数η/μ0也是泥浆体积浓度(Cv)、细颗粒含量百分数、颗粒容重和温度的函数。

2.6 粘稠度系数和流动指数

非牛顿流体是幂律体，其流变议程为:

式中：K为泥浆粘稠度的系数，K值越大粘稠性越大。n=1为牛顿流体，因此n是表示泥浆偏离牛顿流体的程度，称为流动指数，一般n<1。

2.7 泥浆腐蚀率和磨损米勒数

泥浆腐蚀是一种电化学现象，由于颗粒的存在，特别在含氧的情况下，泥浆的腐蚀率比水大。腐蚀率用每年腐蚀管壁厚的毫米数表示(mm/a)，也可用每年腐蚀的米勒数表示(1米勒=0.025 4 mm)。

泥浆中的固体颗粒对输送设备等有磨损作用。为了给泥浆的磨损性提供一个相对衡量的指示，用测定一个标准金属块在泥浆中往复运动后金属的重量损失量来确定，即用米勒数Nm来表示。一般认为Nm>50的泥浆具有较大的磨损性。

3 泥浆的流动特性

对于泥浆流动特性的研究，我们主要研究泥浆的过渡流速(临界流速)，管道的压力损失。 根据其流动性的差异，对于均质的、非均质的泥浆进行了研究。

3.1 均质泥浆的流动特性

均质体的泥浆有两种状态：一种为牛顿流体，一种为非牛顿流体，一般大部分状态为非牛顿流体。

3.2 均质性泥浆的判定

用悬浮指数Z作定量判断的标准，认为Z≤0.19为均质体。

Z=w/kv

式中:w——颗粒沉速；

v——磨阻流速；

k——系数。

从工程实际可操作性出发，瓦斯普等将管道截面上的浓度变化值作为一种区分标准。其内容是：在管道界面直径0.8处的浓度与管道中心的浓度之比值做为衡量的指标，大于0.8为均质体泥浆。

3.3 过渡流速

对于大部分的均质体为非牛顿流体，管道内的流速与其压力损失为函数关系。当管道内的平均流速比较高时，管内的流体状态为紊流状态，其流阻与管内平均流速的1.75～2.00成正比；当管内的平均流速比较低时，管内的流体状态为层流，其流阻与管内的平均流速的一次方成正比。从层流变为紊流的这一临界点的流速就叫做粘性过渡流速。其计算方法会因流体的差异、雷诺数表达形式的差异，而有所不同。

3.4 磨阻损失

均质泥浆的在管道中因流速的差异，分为紊流与层流，两种不同的流动状态在管道中的磨阻损失差异比较大，因而研究方法也有差异。

3.4.1 层流磨阻损失

3.4.1.1 宾汉体

对宾汉体而言，其简化后的方程式为：

3.4.1.2 幂律体

泥浆的有效粘度μe与雷诺数Re3的关系如下：

3.4.2 紊流的磨阻损失

3.4.2.1 宾汉体

在泥浆的光滑过渡区，假定为布拉休斯型，其公式如下：

式中:A1——系数，取A1=0.18；

B——指数，取B=0.167；

Re——定义同前。

通过大量的数据测试，我们以刚度系数来确定雷诺数，在泥浆的过渡状态及紊流状态下，前面的f值均与雷诺数有对应的关系，并且牛顿流体的值大于宾汉体的值。在初步估算时，可取牛顿流体的穆苗图上的f值乘以0.85或0.9作为修正值。

3.4.2.2 幂律体

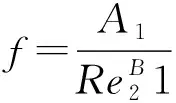
在上式中，m与A1,B1的变化关系如表3所示。

表3 A1、B1与m的关系

当m=1.0时即为清水，此时A1=0.079，B1=0.25。

3.5 非均质性泥浆的区分

根据流动环境的不同，我们把非均质体泥浆看做伪均质体泥浆来进行研究。在工程实例当中，金属矿精矿泥浆和尾矿泥浆属于这种情况。

在工程实际当中，我们更多采用托马斯和查里斯理论。这个理论能更好的解决实际工程当中环境的影响，其方法与实际测试的结果比较相近。其理论为：采用两个参数作为研究对象，泥浆中的固体颗粒沉降速度、输浆管道当中的磨阻流速，并用两个参数的比值作为一个数据来进行对比。

瓦斯普等仿照均质性判定标准，仍采用浓度比C/CA≤0.1为非均质泥浆。同样ZC≈C/CA=10 。

在目前的工程设计中，输送管道的泥浆固体颗粒必须达到C/CA≥0.5～0.6，将此数字作为设计标准之一。

3.6 临界(沉积)流速

在泥浆的输送过程中，一方面需要将管道内的流速降到最低，节能节电；一方面泥浆在输送过程中不能沉淀或泥浆当中固体颗粒尽可能在管道的下部沉淀磨擦管道。因此引入一个临界流速满足以上两方面的功能，在输送当中固体颗粒保持悬浮而不沉淀，一般在工程实际运行当中实际流速要稍高于临界流速，以达到实际工程的要求。 对于不同的泥浆有不同的临界流速，对于不同的工况有不同的临界流速。影响临界速度有内部的因素，也有外部的因素。内部因素有：固体颗粒的容重，固体颗粒的大小，泥浆静止沉淀的速度，固体颗粒的形状系数，泥浆的浓度，泥浆的临界流速，泥浆的粘度，泥浆的最大沉淀浓度，泥浆的化学性质等多种因素；外部因素有：管道的通径，管道内径的粗糙度等因素。

在一般的临界流速计算中，建立数学模型的方法为量纲分析法、经验和半经验验证法。

在工程设计中，我们最常采用杜兰德公式，如下式所示：

式中F为—常数(此数值与泥浆的体积浓度、泥浆的固体颗粒的平均直径均有关系) 。

式中FL为常数(此数值与泥浆的体积浓度有关)，上公式也叫瓦斯普公式。

3.7 磨阻损失

在工程实际应用中，我们将非均质泥浆的磨阻损失作为研究对象。经过实验验证，管道的磨阻损失与泥浆的流速具有一定的关系。在大部分工程实例中，都是水-固混合的泥浆，在高、中、低流速下，泥浆会呈现出不同的状态，并且管道的磨阻损失的坡降线差别非常大(磨阻损失坡降线都以水作为参照)。有的磨阻损失与清水的平行，有的呈下降为缓，有的呈上升趋势坡降线。

在工程实际应用中，由3种不同的环境计算泥浆输送管道的磨阻损失坡降。

3.7.1 均匀粒级组成的非均质泥浆

在工程实际应用中，泥浆管道的磨阻损失坡降，先计算同类型清水的磨阻损失坡降，在加上折合成清水的磨阻坡降。

3.7.2 非均匀粒级组成的非均质泥浆

在实际的工程中，泥浆中的固体颗粒非常复杂，从解决问题的角度出发，为了简单化计算泥浆的磨阻坡降，我们假定固体颗粒为均匀的，其参数均可代表非均匀的固体颗粒的粒径，或表征其固体颗粒的特性。

3.7.3 泥浆中固体颗粒直径级别较大的非均质泥浆

在输送的泥浆当中，有些泥浆中细颗粒比较多(325目)，这部分颗粒与水形成一种混合体，呈现出均匀的伪均质体，这部分在实际工程上也称作“载体”。由于泥浆中固体颗粒直径级别较大，这部分泥浆又与直径比较大的固体颗粒形成非均质体泥浆，这种状态叫做“复合系统”。

在工程实际应用中，用瓦斯普的叠加法来计算“复合系统”的磨阻损失坡降。 先计算伪均质体的磨阻损失，再计算非均质体泥浆的磨阻损失，对两部分进行叠加，所得的数值即为“复合系统”的磨阻损失坡降。

在计算磨阻损失坡降中，要进行多次假设，多次验算才能获取最佳的实际数值，同时又要对各种泥浆进行分类，按照不同的方法进行试算。

4 结语

在实际工程应用中，影响泥浆输送的因素很多，但要对某种泥浆进行输送时，就要对输送的工况做出细致的分析。根据输送浆体的浓度、容重、流动性能来选择合适的泵型进行初输送，再根据输送泥浆的临界速度，确定管道合适的管径，根据泥浆对输送管道的磨损或腐蚀来确定管道的材质或壁厚，根据泥浆对管道的阻力损失，来确定输送系统的管道损失，由起始压力到输送距离的压降最后确定系统的最大压力，从而确定系统的所需功率。在对一个输送系统进行设计时，不同的泥浆的输送方式可能会差别比较大。在日益专业化的设备使用的大背景下，追求最经济的运行成本，最小的投资，最少设备管理人员，这将是检验输送系统设计的最优化的根本。只有对输送系统所要输送泥浆的各种物理指标，流动性，化学指标进行详致的研究，才能设计出合适的泥浆输送系统。