双级气体减压器稳定性影响因素数值分析

孙 冰 许 琪 陈 阳

(北京航空航天大学 宇航学院，北京100191)

位立军

(中国人民解放军93469部队，石家庄050071)

气体减压器是气路系统中重要的降压和稳压元件，它的稳定工作保证了气路系统输出稳定的符合设计压强范围的气体工质，进而保证了任务的顺利完成，因此有必要对其稳定性进行详细研究.现今，减压器的稳定性研究主要采用试验或数值计算手段，进行试验验证可以很好地解决该问题，但必须承担所带来的高成本及高风险，而采用计算机数值仿真可以在极低的成本和风险下达到同样的效果.

单级减压器动态特性的数值仿真研究已经比较充分［1-11］，其区别在于各模型之间的复杂程度不同，部分模型采用了各腔室气体等温［1-4］、绝热［6-7］或非线性方程线性化［7］等与实际情况有所出入的假设，或者对各腔室及运动部件的作用力考虑不够全面［1，6-7］，或者在阀芯或孔处的节流计算上采用了基于压差的节流模型［8］，文献［9］从可压缩瞬变流一维连续和能量方程出发，在有限元状态变量模型［10］的基础上拓展获得可考虑变体积容腔的气体容腔模型，并与气体管道、阀门的数值模型一起组合建立了针对气体减压器的有限体积模型，但没有考虑容腔体积变化所带来的流体膨胀功.文献［11］在此基础上通过考虑膨胀功建立了更全面的有限体积模型.

现今对减压器稳定性的研究主要基于对数值计算结果的分析，进而给出部分影响参数的概括性结论［2-8，12］，文献［2-8］考虑了部分结构或控制参数的单参数影响，但没有给出直观的量化结果以评判各参数对减压器稳定性的具体影响，文献［12］考虑了多参数共同作用下的稳定性变化，但也存在相同的问题.

本文将文献［9，11］的建模方法拓展至双级气体减压器上，建立该型减压器的有限体积瞬态模型，随后针对某用于研究该型减压器动特性的地面试验台建立数值模型，通过大量仿真研究A和B两型具有细微设计差异的减压器各结构参数对稳定性的影响并对相同结构参数下的不同结果进行了比较，最后根据工程需要，选取A型减压器二级阀芯质量、低压腔体积、反馈腔体积及膜片刚度等4个参数，以二级阀芯运动速度的样本方差为稳定性指标，比较各结构参数变化所带来的不同的稳定性影响程度，以指导减压器的设计和改进.

1 双级减压器结构和数学模型

气体减压器把从气瓶出来的气体压力降低到系统要求的压力，其工作原理是由于气体从高压腔通过以活门与活门座之间形成较小的横截面积进入低压腔时发生节流，使气体压力下降.事实上，节流的本质在于高压腔中具有压力能的气体经过活门与活门座间时其压力能转换为动能且这里气体的动能损耗到许多的摩擦上，气体进入低压腔时伴随着气体的减速，于是，气体的压力就发生了下降［13］.图1所示为双级气体减压器的结构示意图，此类减压器属于串联双级冗余高压卸荷膜片式减压器，主要是为了解决单级减压器的单点故障、提高气路系统的可靠性而研制.图中实线结构为A型减压器所具有的结构，虚线部分为B型减压器相较A型而言多出的一级副弹簧及一级膜片结构，两型减压器在设计上有细微区别但其减压原理是一样的.

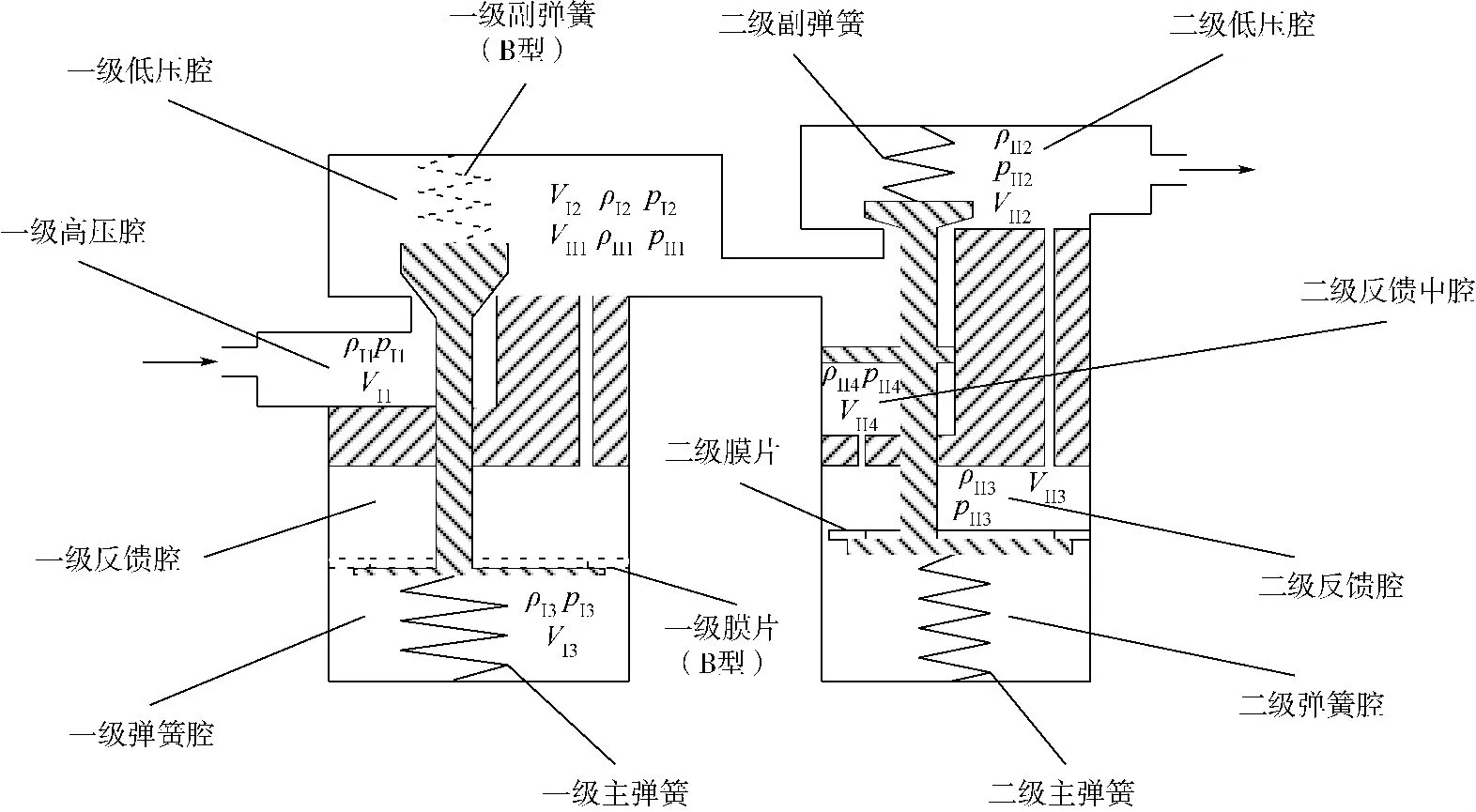
图1 双级气体减压器结构示意图Fig.1 Schematic diagram of dual-stage gas pressure reducing regulator structure

图2所示为双级气体减压器的有限控制体积网格，此网格应用有限体积法理论简化双级减压器结构而来并对其进行了交错处理［14］，其边界处为相邻气体管道的边界网格，把减压器看成由一级高压腔、一级反馈腔、一级低压腔(即二级高压腔)、二级反馈腔、二级反馈中腔、二级低压腔6个气体容腔组合而成，气体容腔之间由节流组件连接.对于容腔体积随两级阀芯开合变化较大的腔室，需要视为变体积气体容腔，本文对减压器一级高压腔、一级低压腔(即二级高压腔)和二级低压腔进行了变体积处理.其有限体积模型由文献［9，11］中的单级调节阀扩展而来，这里不再列出.

图2 双级气体减压器有限控制体积网格Fig.2 Finite control volume grids of dual-stage gas pressure reducing regulator

2 减压器特性研究系统数值模型

图3所示为双级气体减压器特性研究系统的数值模型，图中对各管道的长度(单位:m)、外径(GP5处为内径)和厚度(单位:mm)作了标注，此系统可以模块化［9-11］分解为1个流体源(FS1)、1个气体容腔(GVol1)、1个双级气体减压器(DSGPRR1)、3个气体阀门(GV1～3)、5段气体管道(GP1～5)，其中气体管道模块流场网格一般为100 mm/网格(最少3个网格)，集中参数类元件(例如气体阀门)沿管路走向的长度为2个标准网格单元(初始和末端元件为1个单元)，即200 mm.气体管道、气体阀门、双级气体减压器3种模块元件采用管壁径向一维传热模型，其壁面径向网格数为4，气体容腔模块元件采用管壁零维传热模型［15］.GV3及FS1分别设定为孔板和大气边界条件，这两个组件组合来看其作用等效为流量出口边界条件.

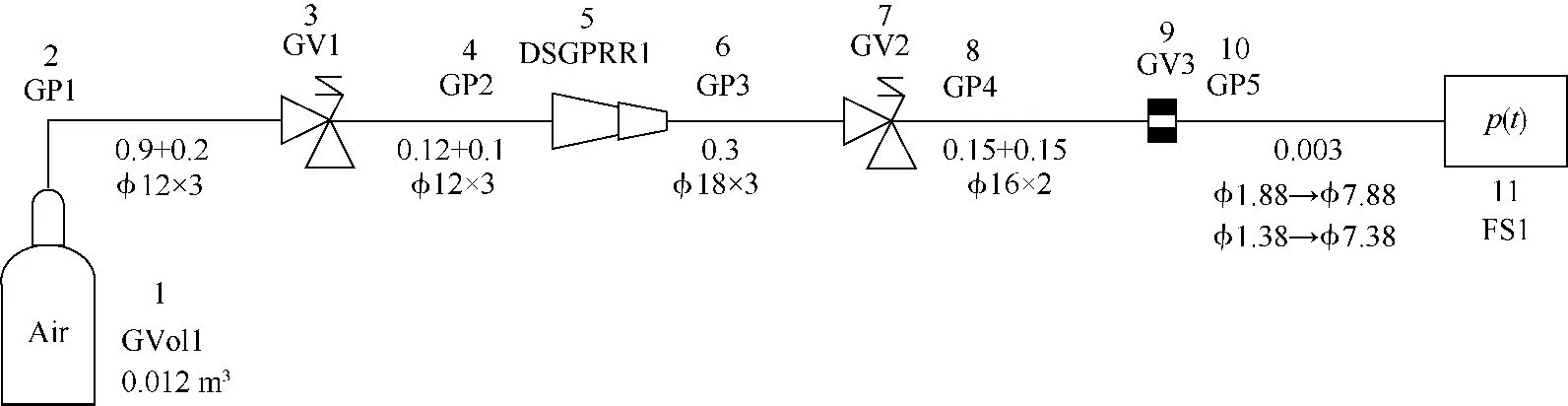
图3 双级气体减压器特性研究系统数值模型Fig.3 Numerical simulation model of the dual-stage gas pressure reducing regulator test system

阀门GV1和GV2在系统起动前分别处于闭合和全开状态.系统起动时打开GV1，从高压气瓶GVol1流出的高压空气冲击到双级减压器DSGPRR1处，此时减压器由于各级低压腔和反馈腔压强很小且处于完全打开状态，于是其压强将会逐渐升高，相应的一、二级阀芯会逐渐运动至额定开度状态，从而，高压空气经减压器两级减压后通过孔板GV3流出，形成稳定流量的射流.系统工作情况因此可分为3个过程:GV1未打开前的无流动阶段，GV1打开后的减压器两级低压腔建压(阀芯闭合)阶段，额定开度状态下的稳定射流阶段.

系统起动时刻初始状态设置如下:GVol1～GV1上游腔之间管路压强为 p0，GV1下游腔 ～GV2上游腔之间管路压强为p1，GV2下游腔之后管路压强为p2，管路温度为T0;气瓶体积为V0G.针对A和B型双级减压器算例的参数设置见表1～表3，两型减压器在参数上的差异由符号“/”相隔，前者代表A型、后者代表B型，如无不同则只有一个数据.

表1 双级气体减压器特性研究系统初始参数设置Table 1 Initial parameters for dual-stage gas pressure reducing regulator test system

表2 双级气体减压器结构参数设置Table 2 Structure parameters for dual-stage gas pressure reducing regulator

3 结构参数稳定性影响分析

为了使减压器输出的气体压力和流量符合工程设计要求，有必要使减压器处于稳定工作的状态，即保证其输出幅值在设计范围内且没有剧烈的振荡，此外，为了保证减压器的工作性能，需要使减压器起动时间尽可能短，即防止“时滞效应”的出现.因此可通过研究减压器阀芯的动态性能来探寻减压器稳定工作的基本规律.在大量的时域仿真计算过程中，发现双级减压器的总体稳定性与减压器二级结构参数直接相关，即在减压器一级出现明显不稳定情况下可通过改变减压器二级结构参数使减压器输出气体压强及流量符合设计要求，但如果减压器二级出现明显不稳定情况时是无法通过改变减压器一级结构参数来使减压器输出符合设计要求.因此为了更好地指导工程实际只在表2中列出了A和B两型减压器二级各结构参数对减压器稳定性影响的结果，该表中每一结构参数栏中的上层数据为A型减压器结果、下层为B型减压器结果.该表以表1中的结构参数为标准算例，各结构参数仿真范围参见表4并以减压器阀芯开度随时间变化的动态曲线作为判断减压器稳定性的标准，给出了减压器各结构参数变化所对应的稳定性变化情况以及合理的结构参数变化范围.

从表4中，可以看到绝大部分结构参数的稳定性变化规律都是单调的，比较特殊的是A型、B型参数lII4和A型参数dvII3，参数lII4在A型减压器下不论增大还是减小其稳定性都有所下降，但仿真结果所呈现的阀芯振荡并不剧烈，于是笔者认为在工程上可以任取lII4的值，而B型减压器稳定性基本不受该参数变化的影响;A型参数dvII3随着数值的增大其稳定性变化会出现反复.此外，A型参数 lI2，lII3，dvII3，αII，dvII1，CmII都在稳定性持续增强的一端出现“时滞效应”，虽然此时减压器稳定性很好，但出现了“时滞效应”所带来的起动时间延长，B型参数dvII3和dvII4随着减压器稳定性的增强其输出压强出现了超过设计要求的压强峰，于是本文仍然给出了相应结构参数取值的上(下)限.通过对比两型减压器在同一结构参数下的稳定性变化规律，笔者发现具有相同减压原理的不同减压器稳定性变化规律在大部分情况下是相同的，但在参数lII4，dvII3，dvII4上存在不同规律，因此对于新型减压器的研究在原有基础上还需进行试验或数值仿真从而获得可靠的结果.

表4 双级减压器二级结构参数变化对减压器稳定性的影响结果Table 4 Results of stability as a function of modifying the regulator II-stage structural parameters

表4的结果可以为该型减压器的相关设计人员提供数值支持，以便其进一步改善减压器性能或设计新型减压器，但不足之处是各稳定性影响因素之间改善减压器稳定性效果的区别没有得到体现，于是各结构参数对稳定性影响程度的研究就显得尤为重要.基于此，针对A型减压器，根据工程需要选取减压器二级阀芯质量、低压腔体积、反馈腔体积及膜片刚度4个参数作为研究对象着重研究二级结构参数变化所带来的不同的稳定性影响.

为了易于计算且能直接反映减压器工作状态，本文选取减压器二级阀芯运动速度的样本方差作为双级减压器的稳定性指标，样本方差为

其中，xi为各样本值;E(x)为样本期望;n为样本总数.在本文中，xi即为减压器二级阀芯瞬时运动速度，E(x)为各样本平均值，稳定性指标结果越低表示减压器越稳定，反之则表示不稳定，本文所取的时间样本点的范围为2～10s.表5为本文分析所用到的各算例结构参数具体数值，其取值方法都是沿使减压器趋于不稳定的变化方向相对标准算例从1%变化到10%，每个结构参数都有10个算例，各算例有400个样本点，算例0-0为标准算例.

表5 稳定性指标计算算例Table 5 Calculation cases on stability index

图4所示为4个结构参数稳定性指标计算结果，横坐标为各算例所取结构参数值相对标准算例变化率的绝对值，纵坐标为稳定性指标，其坐标刻度经过了对数化处理.如图4可知，相对变化率在0～0.02范围内时，各结构参数的稳定性指标都在很低的水平，且变化幅度很小;当相对变化率处于0.02～0.04范围内时，原本稳定性指标最低的mVCII曲线会迅速爬升且远远大于其余3条曲线，而其他曲线的变化幅度和相对大小基本不变;当相对变化率为0.04～0.06范围内时，CmII曲线也会大幅爬升，但其数值仍明显小于mVCII曲线，而其余两条曲线的增长幅度依然偏低;随着相对变化率的继续变大，各曲线平稳变化，但由于纵坐标为对数坐标，各曲线之间的变化幅度存在倍数上的差别.综合来看，在仿真范围内各结构参数稳定性指标的变化幅度按从大到小排列为:mVCII＞CmII＞lII2＞lII3.因此，对于该型或具有该型减压方式的双级减压器，如果减压器出现了一定程度的振荡，设计人员可以优先减小二级阀芯质量或增大膜片刚度从而更快地改善减压器的稳定性.

图4 结构参数稳定性指标计算结果Fig.4 Structure parameter stability indexes

4 结论

本文在对具有相同减压原理的两型双级减压器不同结构参数进行大量时域仿真所得到的各结构参数变化对减压器稳定性的影响规律的基础上，选取减压器二级阀芯运动速度的样本方差作为稳定性指标，计算了减压器二级阀芯质量、低压腔体积、反馈腔体积及膜片刚度4个结构参数在2～10s及参数变化10%的范围内的稳定性指标.结果表明，在仿真范围内各结构参数稳定性指标的变化幅度按从大到小排列为:mVCII＞CmII＞lII2＞lII3.因此，设计人员可以优先减小二级阀芯质量或增大膜片刚度从而更快地改善减压器的稳定性.本文的分析方法可以对减压器稳定性各影响因素进行筛选，从而获得最优的改善方法，进而帮助相关设计人员以最小的代价获得满足工程要求的结果.

References)

［1］张雪梅，张黎辉，金广明，等.减压器动态过程的数值仿真［J］.航空动力学报，2004，19(4):541-545 Zhang Xuemei，Zhang Lihui，Jin Guangming，et al.Numerical simulation of the dynamic process for pressure regulator［J］.Journal of Aerospace Power，2004，19(4):541-545(in Chinese)

［2］郑丽，李清廉，沈赤兵.大流量气体减压器响应特性的仿真研究［J］.火箭推进，2008，34(2):18-23 Zheng Li，Li Qinglian，Shen Chibing.Analysis on responding characteristics of large flux pressure reducing valve［J］.Journal of Rocket Propulsion，2008，34(2):18-23(in Chinese)

［3］赖林，李清廉，郑丽，等.大流量气体减压器振动问题研究［J］.国防科技大学学报，2009，31(2):1-4 Lai Lin，Li Qinglian，Zheng Li，et al.Research of the vibration failure of the large flux PRV［J］.Journal of National University of Defense Technology，2009，31(2):1-4(in Chinese)

［4］余中军，赵竞全.航空氧气减压器性能仿真分析［J］.北京航空航天大学学报，2009，35(11):1379-1383 Yu Zhongjun，Zhao Jingquan.Simulation on pressure regulator characteristic［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(11):1379-1383(in Chinese)

［5］尤裕荣，曾维亮.逆向卸荷式气体减压阀的动态特性仿真［J］.火箭推进，2006，32(3):24-30 You Yurong，Zeng Weiliang.Simulation on reverse balanced pneumatic pressure reducing valve dynamic characteristic［J］.Journal of Rocket Propulsion，2006，32(3):24-30(in Chinese)

［6］陈晓琴.减压阀充填过程动态特性仿真［J］.导弹与航天运载技术，2006(5):45-49 Chen Xiaoqin.Dynamic simulation of the pressure reducing valve in filling conditions［J］.Missile and Space Vehicle，2006(5):45-49(in Chinese)

［7］ Zafer N，Luecke G R.Stability of gas pressure regulators［J］.Applied Mathematical Modelling，2008(32):61-68

［8］ Rami E G，Jean-Jacques B，Bruno D，et al.Modelling of a pressure regulator［J］.International Journal of Pressure Vessels and Piping，2007(84):234-243

［9］陈阳，高芳，张黎辉，等.减压器动态仿真的有限体积模型［J］.推进技术，2006，27(1):9-14 Chen Yang，Gao Fang，Zhang Lihui，et al.Finite volume model for numerical simulation on dynamic process of pressure reducing regulator［J］.Journal of Propulsion Technology，2006，27(1):9-14(in Chinese)

［10］张育林，刘昆，程谋森.液体火箭发动机动力学理论与应用［M］.北京:科学出版社，2005 Zhang Yulin，Liu Kun，Cheng Mousen.Liquid rocket engine dynamic theory and application［M］.Beijing:Science Press，2005(in Chinese)

［11］陈阳，高芳，张振鹏，等.气动薄膜调节阀控制系统工作过程的动态仿真［J］.火箭推进，2006，32(6):28-34 Chen Yang，Gao Fang，Zhang Zhenpeng，et al.Dynamic simulation of working process for control system of a pneumatic diaphragm control valve［J］.Journal of Rocket Propulsion，2006，32(6):28-34(in Chinese)

［12］陈阳，蔡国飙，张振鹏，等.双组元统一推进系统减压器稳定性仿真［J］.北京航空航天大学学报，2010，36(10):1135-1139 Chen Yang，Cai Guobiao，Zhang Zhenpeng，et al.Numerical simulation on dynamic stability of pressure reducing regulator in integral bipropellant propulsion system［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(10):1135-1139(in Chinese)

［13］廖少英.液体火箭推进增压系统［M］.北京:国防工业出版社，2007 Liao Shaoying.Liquid rocket propellant and pressurization feed system［M］.Beijing:National Defense Industry Press，2007(in Chinese)

［14］李人宪.有限体积法基础［M］.2版.北京:国防工业出版社，2008 Li Renxian.Finite volume method［M］.2nd ed.Beijing:National Defense Industry Press，2008(in Chinese)

［15］ Chen Y，Cai G B，Wu Z.Modularization modeling and simulation of turbine test rig main test system［J］.Applied Mathematical Modelling，2011，35(11):5382-5399