阻尼网特性数值模拟

丛成华 廖达雄

(1.中国空气动力研究与发展中心 空气动力学国家重点试验室，绵阳621000;2.中国空气动力研究与发展中心 设备设计及测试技术研究所，绵阳621000)

风洞设计中，为了整流一般需要布置阻尼网，安装在稳定段中用于降低湍流强度，安装在大角度扩散段中用于抑制分离.为提高流场品质和降低压力损失，必须合理布置阻尼网，并合理选择阻尼网参数.阻尼网不仅用在风洞整流中，它还广泛应用于工农业中，如造纸中的除水干燥过程、农业中的病害虫隔离、防风沙等都需要用到阻尼网［1］.

由于其重要性，半个多世纪以来，针对阻尼网已经进行了大量的理论研究和试验研究.阻尼网的研究可以追溯到Prandtl，他首先认识到阻尼网可以控制速度的均匀性［2］.Schubauer在1947年就完成了不同流速下的阻尼网压降特性和降湍特性测试，给出了阻尼网的尺度效应［2］.Baines等人研究认为开孔率低于0.5时流动容易受到阻尼网的扰动而出现射流合并(jet coalescence)导致流动失稳，采用开孔率高于0.5的阻尼网时才能起到抑制湍流的作用［3］，Mehta认为这一数值应为0.57［4-5］.Dadone 等人发展了一种新的理论-试验方法以确定阻尼网压降特性，对比了不同速度下的压力损失结果;他研究认为开孔率越低，来流速度对损失系数K的影响越大，在每个开孔率下，都有某个对应速度使得K最小，速度减小或增加都会导致K增加，在开孔率大于0.57时来流速度的影响降低［6］.Nevelsteen发展了体阻力模型，给出了风扇旋流条件来流情况下阻尼网K的确定方法［7］.Laws等人研究了通过阻尼网的速度分布和流动方向［8-9］.Groth等人研究了具有中等湍流强度，均匀、垂直来流情况下阻尼网的降低湍流问题，认为亚临界雷诺数为 40［10］.Derbunovich 等人通过试验研究了阻尼网数量、外形参数和位置对湍流的抑制作用［11］.

为了获得最优的速度均匀性和压力恢复，Sahin在45°和60°扩散段中对阻尼网开孔率和布置位置进行了试验研究，并建立一维数学模型进行了分析［12］.Hancock理论分析了任意损失系数、任意距离、任意数量的阻尼网在消除扩散段速度非均匀性方面的效应［13］.Kulkarni通过数值模拟将阻尼网参数与布置方式进行优化的成果应用到了风洞设计中，试验结果证明了优化设计方案的可行性［14］.

在这些研究中，还没有对阻尼网的流场特性和参数进行详细的研究，本文采用数值模拟研究了阻尼网的三维流场和局部流动细节，并与试验数据进行了对比，为合理选择阻尼网提供支撑.

1 阻尼网参数和建模

影响阻尼网性能的本体参数包括网丝直径d、网孔宽度 w、单元尺寸 l(l=w+d)、开孔率 β(β=w2/(w+d)2)、目数 M(M=1/l)、编织形式等，阻尼网性能还与来流条件密切相关，如来流速度大小、来流方向、入口速度型、边界层参数、湍流强度等，在当前研究中，采用均匀来流条件，仅考虑本体参数对性能的影响.因此来流条件可用雷诺数表征:

式中，U∞是来流速度;U0是阻尼网处速度;ν为运动黏性系数.入射速度与阻尼网平面的夹角为θ;出流速度与阻尼网平面的夹角为φ.

阻尼网有平纹编织和斜纹编织等形式，本文研究的阻尼网采用平纹编织形式，见图1.建模时，包含了入口段和出口段，入口段长度取60d，出口段长度取600d.以水平方向为y轴(即入口气流流向)，垂直方向为x轴，按右手法则设定z轴建立坐标系，将阻尼网平面中心设定为坐标原点.

图1 用于CFD的阻尼网模型图Fig.1 Model view of screen using in CFD

2 数值方法

阻尼网绕流就是绕圆柱的流动，雷诺数小于40时流动是定常层流，大于40后流动成为非定常，150～300之间发生转捩，一直到2×105流动都处于亚临界状态［15］.因此当雷诺数较大时，阻尼网后部存在剪切层和涡脱落，尤其是近壁面附近变量梯度非常大，对数值模拟提出了较高的要求.为简化计算，未考虑流场随时间的变化效应.

2.1 计算网格

采用混合网格，入口和出口采用结构网格，阻尼网附近及壁面处网格采用非结构三棱柱网格，确保阻尼网壁面处网格y+＜5，单孔阻尼网网格规模大概在70万左右，网格拓扑如图2所示.

图2 阻尼网网格拓扑示意图Fig.2 Gird topology view of screen

2.2 控制方程

控制方程使用N-S方程，矢量形式的连续方程和动量方程为

在流场求解中使用有限体积法，压力与速度的耦合方程采用SIMPLE(Semi-Implicit Method for Pressure Linked Equations)算法求解，差分方程采用二阶精度，时间上使用隐式迭代方法推进求解.使用低雷诺数 k-ε 湍流模型［16］.

2.3 边界条件

入口给定均匀速度入口，大小按照试验条件给出，出口为自由流出边界;壁面使用绝热无滑移黏性壁面边界;侧面给定周期边界条件.

2.4 算法验证

阻尼网选择文献［2］中的阻尼网 C:d=0.43 mm，l=1.27 mm，β =0.436，来流速度4.023 m/s.图3给出了压力损失值与试验结果的对比.采用不同数量网格时，压力损失最大差异仅0.1 Pa，且都与试验结果相近，误差在2.3%以内，因此当前采用的网格都能满足计算要求，为减小网格对计算结果的影响，单孔选用70万网格进行计算.

图3 不同网格数量时计算压力损失与试验结果对比Fig.3 Total pressure loss of experiment and CFD with different gird cells

3 阻尼网流动特性

3.1 损失系数确定方法

阻尼网最重要的是确定损失系数K，定义为

其中，ΔP为总压损失;Pd为来流动压;Pin与Pout分别为阻尼网入口与出口总压.

在工程实践中，发展得到了很多经验公式，文献［17］列举了一些形式上较为简单的经验公式，这些公式仅与开孔率相关，未考虑雷诺数的影响，且开孔率的适用范围较为有限.Aljabari［18］根据圆柱阻力理论推导的经验公式仅适用于雷诺数小于600的情况.Perry［19］给出的公式误差在20%左右，低雷诺数时误差更大.Wieghardt［20］给出的公式在雷诺数大于600后保持常数，在计算高雷诺数流动时精确性降低.笔者在实际使用过程中发现 Idelchik［21］和 Brundrett［22］给出的经验公式适用性较好.表1给出了文献［2］中不同阻尼网的损失系数结果.阻尼网 B:d=0.2 mm，l=1.06 mm，β=0.672;阻尼网 F:d=0.14 mm，l=0.47 mm，β=0.494;阻尼网 J:d=0.34 mm，l=0.64 mm，β=0.212.可以看到，经验公式给出的结果与试验结果都有差异，Idelchik给出的公式需要查阅图表，精确性较Brundrett的差一些.CFD给出的结果与试验结果最为接近，在实际使用中，采用CFD进行阻尼网损失系数的计算将更为精确.

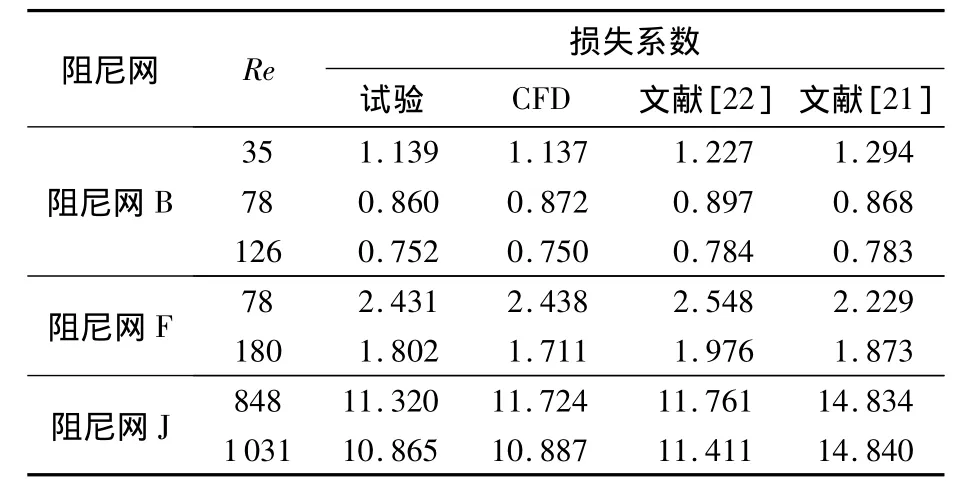
表1 不同阻尼网损失系数Table 1 Total pressure loss coefficient of different screens

从表1中也可以看出，对于同一阻尼网，随雷诺数增加，阻尼网损失系数下降;当阻尼网开孔率降低时，损失系数急剧增大.

3.2 雷诺数对流动特性的影响

图4给出了阻尼网B单元中心线的速度分布，在雷诺数小于40时，流动由于基本保持层流状态，扰动在短距离内恢复，而随着雷诺数的增大，流动逐渐转化为非定常流动，扰动传播的距离明显增加.从图4看到，速度扰动要在阻尼网后40 cm左右即30l～40l处才能恢复，而Groth等人认为这一距离为 15l～20l［10］，Derbunovich 等人认为20l以后速度脉动的恢复量急剧减小［11］，根据当前的计算结果，这一距离明显要延长.这对布置阻尼网具有指导意义，尤其是布置多层阻尼网时，阻尼网间距要保证扰动得到充分衰减.

从图5可以看到，在流过阻尼网时，流动收缩进入阻尼网，速度明显升高(图中的速度采用来流速度U∞进行了归一化处理)，且随雷诺数增大，收缩效应增强，阻尼网对流动的扰动增加.从流线可以看出，当雷诺数小于40时，阻尼网单元之间不存在流质的交换，可以认为基本保持为层流状态，当雷诺数大于40以后，阻尼网的流动性态发生了明显的变化，下游出现了薄剪切层和涡脱落，单元之间出现了流质交换;随雷诺数增大，流质交换量增加.这与Groth［10］给出的亚临界雷诺数相对应.为提高阻尼网降湍能力，应将雷诺数限定在40以下.

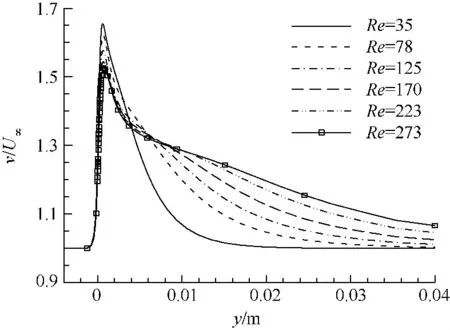
图4 不同雷诺数时阻尼网B后中心线速度分布Fig.4 Velocity distribution of centerline after screen B with different Re

图5 不同雷诺数时阻尼网B的速度分布Fig.5 Velocity coutour of screen B with different Re

3.3 开孔率对流动特性的影响

从图6给出的不同开孔率阻尼网速度分布可以看出，当开孔率低于0.436后阻尼网C后的流动出现失稳，当开孔率降至0.212时阻尼网J后出现了大范围分离，这将大大增加阻尼网后的湍流强度.在开孔率为0.494时流动仍保持较为平稳，但阻尼网F后存在分离驻涡，且性态与阻尼网B的分离不同.数值模拟中由于没有时间项，因此预测得到的流动分离为定常分离，考虑到风洞实际运行中来流条件更为恶劣，湍流强度增大，会导致网丝壁面附近的流动与核心流的动量交换增大，分离区会更大一些，流动会发展为非定常间歇性分离，其大小、位置、尺寸都会随时间而改变，产生较大的脉动，因此在风洞整流中，不宜使用开孔率低于0.5的阻尼网.

图7给出了阻尼网后的湍流强度，开孔率低于0.436时，流动失稳导致阻尼网后湍流强度增大，而开孔率大于0.494后都能有效降低湍流强度，而从阻尼网F低雷诺数流动状态看，在Re=78时仍保持层流状态，也可以看到，只要阻尼网后的流动不失稳，开孔率越小，降低湍流的幅度越大.考虑到风洞内灰尘堵塞的影响等，实际的阻尼网开孔率应更高一些，Metha［4-5］推荐采用开孔率大于0.57的阻尼网.

图6 阻尼网J，F，C的对称面速度分布Fig.6 Velocity coutour of symmetry of screens J，F，C

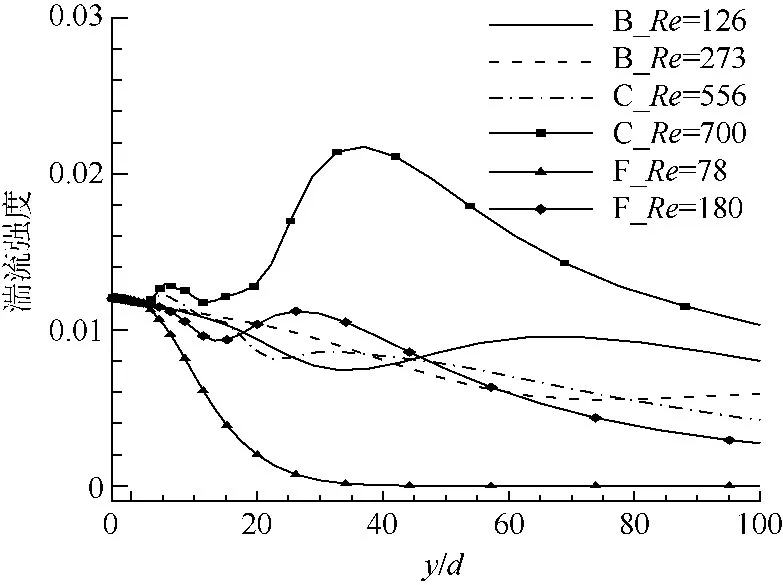
图7 阻尼网B，C，F后中心线湍流强度Fig.7 Turbulence intensity of centerline of screens B，C，F

3.4 入射方向对流动特性的影响

在扩散段内，由于扩散角的影响，当采用平面阻尼网时，入射气流与阻尼网有一定夹角，对有角度入射的情况研究不多，且仅有的经验公式与试验结果差异较大.图8给出了阻尼网 S［4］在不同入射角度θ下损失系数的对比(阻尼网S:d=0.376 mm，l=1.69 mm，1.59 mm，β =0.594)，Brundrett公式在角度较大时与试验结果差异很大，而数值模拟得到的结果与试验值在整个入射角范围内都保持较为接近，差异小于5%.从图上也可以看出，随着入射角度的增加，损失系数下降，阻尼网的整流效能下降，因此在有入射角度时，可适当降低阻尼网开孔率，开孔率的改变按照损失系数下降的幅度进行估算.但考虑到靠近壁面附近损失系数下降较大，过低的开孔率可能会导致边界层附近出现过射(overshoot)，开孔率的改变应采用数值模拟进行评估.

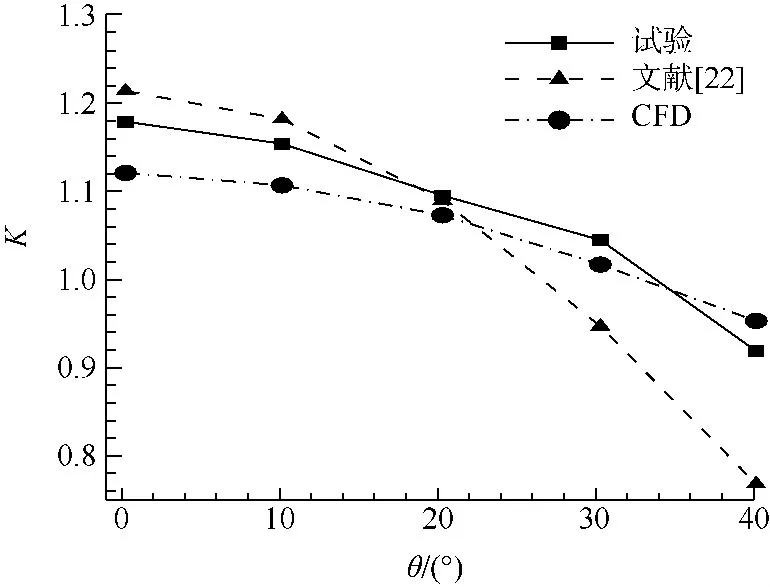
图8 入射角对阻尼网S的损失系数影响Fig.8 Total pressure loss coefficient of screen S with different incident angle

从阻尼网后的总压分布看(图9)，随着入射角的增大，压力损失减少，阻尼网对流动的扰动增加，值得注意的是，在入射角为10°时阻尼网后的压力在较大距离内(＞100d)都呈现脉动趋势，随入射角增加，脉动幅度增加，但延续的距离减小，入射角增加到40°时，压力脉动在30d左右恢复，这在布置阻尼网时需要注意.

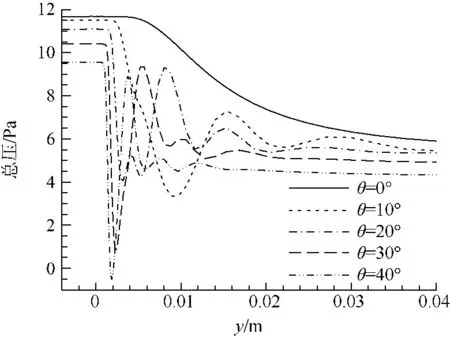
图9 阻尼网S中心线总压分布Fig.9 Total pressure profile of centerline after screen S

当入射角增大时，阻尼网的降湍能力增加明显(图10)，在阻尼网后起始阶段(0～50d)，湍流强度呈明显脉动变化，这主要由于阻尼网对流动产生了较大扰动，尤其是纵向方向;随流动发展，湍流度迅速下降，这可能是由于阻尼网在两个方向上都起到了降湍作用;另外，倾斜入射时，在垂直阻尼网平面方向来流雷诺数减小，降湍能力也得到了增强.

3.5 目数对流动特性的影响

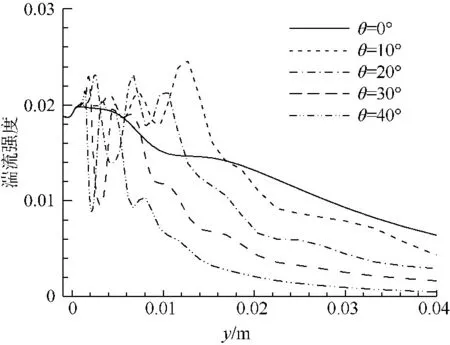
图10 阻尼网S中心线湍流强度Fig.10 Turbulence intensity of centerline after screen S

为研究参数的影响，选择了开孔率0.556的阻尼网［4］，采用不同的目数(M=6，9，15，20，30，40，50，70)，入口速度为 19.917 m/s.表 2 给出了不同情形下的损失系数，可以看到，在相同的开孔率下，随目数增加损失系数增加明显.

表2 相同开孔率不同目数阻尼网损失系数Table 2 Total pressure loss coefficient of screens with the same open ratio and different mesh number

图11给出了湍流强度的沿程变化，可以看到，在阻尼网丝径较大时，湍流强度在350d～400d后才恢复至网前水平.在使用大丝径阻尼网进行降湍时，相邻两层网之间的距离应该大于这个距离，这样有利于阻尼网自身产生漩涡的衰减.在使用小丝径阻尼网时，湍流强度能够得到较快的衰减，为充分发挥阻尼网降湍作用，第2层阻尼网应该布置300d之后，从数值模拟看，两层阻尼网之间的距离较传统经验得到的数值大(伍荣林推荐两层阻尼网之间的距离为20～30 cm［23］).另外，在开孔率保持为常数时，随着目数的增加，降湍能力增加，这与Scheiman［24］的试验研究结果是一致的，这是由于当网丝直径雷诺数达到一定程度时，其自身产生的漩涡会导致湍流度增加.值得注意的是，雷诺数600左右的降湍能力差异明显，在无法保证层流的情况下，选择的阻尼网应该使得雷诺数保持在600以下.

图11 相同开孔率不同目数阻尼网后湍流强度Fig.11 Turbulence intensity of centerline of the same open area ratio screen using different wires per inch

4 结论

1)使用CFD能得到阻尼网不同开孔率在不同雷诺数、不同入射方向的损失系数，结果与试验结果更为接近.

2)雷诺数小于40(最大可以扩展到78)时流动保持层流状态，降湍效果最好，扰动可以在50d～100d内恢复，随雷诺数增加，扰动传播距离增加至350d～400d.

3)在未失稳时，开孔率越低，降湍效果越显著，但开孔率低于0.5时容易失稳.

4)开孔率和来流条件固定时，随目数增加，阻尼网损失系数增加明显，降湍能力提升.

5)为提高降湍能力，两层阻尼网之间的间距应大于300d，雷诺数应小于600.

污垢和表面氧化对阻尼网性能影响很大，损失系数会增大30%以上［19］，对降湍效果影响非常大［25］，下一步将研究阻尼网物理损坏和表面污垢等对阻尼网性能的影响.

References)

［1］ Teitel M.On the applicability of the forchheimer equation in simulating flow through woven screens［J］.Biosystems Engineering，2011，109:130-139

［2］ Schubauer G B.Aeodynamic characteristics of damping screens［R］.NACA-TN-2001，1950

［3］ Baines W D，Petersen E G.An investigation of flow through screens［J］.Transactions of ASME，1951，73:467-480

［4］ Mehta R D.Turbulent boundary layer perturbed by a screen［J］.AIAA Journal，1985，23(9):1335-1342

［5］ Mehta R D.Boundary layer two-dimensionality in wind tunnels［J］.Experiments in Fluids，1987，5:358-360

［6］ Dadone A，Napolitano M.Pressure losses through screens［R］.NASA-PUBL-146，1974

［7］ Nevelsteen K.Screen characterization under fan induced swirl conditions［J］.IEEE Transactions on Components and Packaging Technology，2006，29(2):385-394

［8］ Livesey J L，Laws E M.Simulation of velocity profiles by shaped gauze screens［J］.AIAA Journal，1973，11(2):184-188

［9］ Laws E M，Livesey J L.Flow through screens［J］.Annual Review of Fluid Mechanics，1978，10:247-266

［10］ Groth J，Johansson A V.Turbulence reduction by screens［J］.Journal Fluids Mechanics，1988，197:139-155

［11］ Derbunovich G I，Zemskaya A S.Optimum conditions of turbulence reduction with screens［J］.Fluid Dynamics，1993，28(1):138-144

［12］ Sahin B.The pressure drop and flow characteristics of wide-angle screened diffusers of large area ratio［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，58:33-50

［13］ Hancock P E.Plane multiple screens in non-uniform flow with particular application to wind tunnel settling chamber［J］.European Journal Mechanics B Fluids，1998，17(3):357-369

［14］ Kulkarni V.Simulation of honeycomb-screen combinations for turbulence management in a subsonic wind tunnel［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99:37-45

［15］康钦军.圆柱绕流的数值模拟［D］.北京:清华大学，1999 Kang Qinjun.Numerical simulation around a circular cylinder［D］.Beijing:Tsinghua University，1999(in Chinese)

［16］ Abid R.Evaluation of two-equation turbulence models for predicting transitional flows［J］.International Journal of Engineering Science，1993，31:831-840

［17］ Grumet A A.Navier-stokes analysis of NWTC back leg diffuser［R］.AIAA-97-0094，1997

［18］ Aljabari S.Prediction of the pressure loss coefficient of wind tunnel turbulence reducing screens［R］.AIAA-92-4043，1992

［19］ Perry R H.Perry's chemical engineers'handbook［M］.6th ed.New York:McGraw-Hill Press，1984:23-24

［20］ Wieghardt K F G.On the resistance of screens［J］.Aeronautial Quarterly，1953，4:186-192

［21］ Idelchik I E.Handbook of hydraulic resistance［M］.3rd ed.Boca Raton:CRC Press Inc，1994:359-361

［22］ Brundrett E.Prediction of pressure drop for incompressible flow through screens［J］.Journal of Fluids Engineering，1993，115(2):239-242

［23］伍荣林，王振羽.风洞设计原理［M］.北京:北京航空学院出版社，1985:47-49 Wu Ronglin，Wang Zhenyu.Wind tunnel design method［M］.Beijing:Beijing Aeronautics Institute Press，1985:47-49(in Chinese)

［24］ Scheiman J.Comparison of experimental and theoretical turbulence reduction from screens，honeycomb and honeycomb-screen combinations［J］.Journal of Aircraft，1981，18(8):638-643

［25］ Scheiman J.Considerations for the installation of honeycomb and screens to reduce wind-tunnel turbulence［R］.NASA-TM-81868，1981