虚拟现实中基于Herm ite曲线实现固定漫游路径算法与优化

裴玉，刘桂阳，师翊

（黑龙江八一农垦大学信息技术学院，大庆163319）

随着社会的进步，虚拟现实技术在计算机领域已经得到了广泛的发展，它能够为使用者提供关于视觉、听觉、触觉等感官的模拟，使用户不用亲临现场就有如同身临其境一般。近年来，虚拟现实技术在城市规划、工程设计、医学、文化传播、旅游、教育等领域有着极为广泛的应用[1]。可以说，虚拟现实技术的综合应用，具有广阔的发展前景和良好的社会、经济效益。虚拟环境漫游是虚拟现实应用的基本功能之一，构造一个虚拟环境漫游系统，就是利用高性的计算机软硬件创建参与者具有身临其境的人机交互能力、有助于启发构思的信息环境[2]。Unity3D作为一种三维虚拟现实游戏平台，是一个全面整合的专业游戏引擎。它可以充分、实时的处理大量的三维模型，使用户在三维场景中真实的感受到被仿真系统运行中的动态变化。

在三维场景中，漫游是一个重要的表现手法。漫游[3]包括自主漫游、固定路径漫游。固定漫游控制路径既可以用于到相机漫游，也可以用于其他虚拟对象的自动运动。如何确定这些路径，在这方面，技术相对已经比较成熟，多数是利用现成的曲线计算，对于普通的二次曲线是可以实现平滑的过程，但是往往这是一个比较复杂的过程，会占用大量的时间。在交互状态下如何去设置控制点，不是很方便，只能用样条曲线。样条曲线的特点是由多个控制点进行拟合的，它的控制点是关键，如何在实际问题中动态的实现这些控制点是一个难题，而且在控制点中，找到中间某个差值，也需要用控制点计算，每步大量的运算，给实时运行造成很大的负担[4]。Hermite曲线已经解决了这个问题，但是它的缺陷是不能在交互状态下去控制，而且实时去每一帧进行计算，会造成大量的资源浪费，影响大量的时间。此研究是在Unity3D场景下用交互的方法，实现了Hermite曲线的动态控制节点，将现实中的路径通过Hermite曲线原理转化成分段的样条曲线，实时生成显示状态，给用户提供了一个可参考的路径，最终将路径固化成具体的节点代码，进行优化。

1 漫游路径曲线的实现原理

1.1 Herm ite曲线实现原理

Hermite曲线已经研究成熟，它可以直观的描述平滑曲线的构建。假设有n个点，分别为P0，……Pi-1，三次Hermite曲线可以由起始点Pi和结束点Pi+2，以及起始切线Ti和结束切线Ti+2来定义[5]。三次Hermite曲线插值公式P（t）可以表示为（其中t∈[0，1]）：

P（t）也称为Hermite曲线段或者三次样条段，该曲线段满足下列等式

Hermite曲线就是通过曲线的起点、终点、起点切向量和终点切向量来确定曲线的。

图1 Herm ite曲线Fig.1 Hermite curve

图1 所示是Hermite曲线及其控制点的示意图。改变这四个参数，就可以控制Hermite曲线的形状。要实现物体做连续的曲线运动，首先离散化该曲线，得到分布在这条曲线上的点。为了使物体运动平滑，那么相邻两点的间隔距离不能太大，否则物体在运动过程中会出现抖动的现象[6]。在计算机图形学中，利用计算得到离散化的点用直线连接起来得到一条近似曲线来绘制Hermite曲线。如果在每一帧中使用物体依次放到这些离散化的点的上，相邻两点的间隔距离足够消失，就可以实现物体沿Hermite曲线的平滑运动。

1.2 路径的生成原理

假设Hermite曲线上有已知的n个点，t是系统时间，从第一帧开始从0无限变大。当前时间为t时，需要计算出填充于两个已知点之间点的坐标，这些点连续成为场景中的Hermite曲线，而坐标位置是关于t的参数方程（t∈[0，1]）。在实际运行中，要求每两个已知点之间的填充点，需要将系统时间t转化到[0，1]，具体做法为：（当前时间-起点时间）/（末点时间-起点时间），将算出的当前时间代入参数方程中，即可求出每个填充点的坐标。

在Hermite曲线中，相邻已知点P1和P2的生成时间为TimeP1=2 s，TimeP2=4 s，如图2所示。

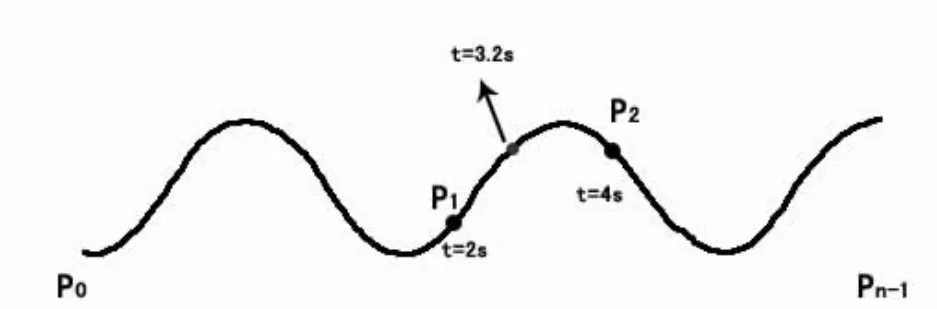
图2 曲线示意图Fig.2 Schematic diagram of curves

若求在3.2 s时生成的点的坐标，应先求当前时间t=（3.2-2）/（4-2）=0.6 s，将t=0.6，代入参数方程

即可求出在3.2 s时生成的点的坐标。

2 交互实现曲线

2.1 交互实现曲线的方法

在Hermite曲线中默认4个点，实际工作中有若干个点，如何把现实中的多个节点转化成Hermite中4个点？假设有n个点，要在这n个点中取出相邻4个点，求出2个点的切向量，用2个点的坐标和这2个点的切向量确定填充点的坐标。将所有已知点的坐标放在一个数组里，初始化每个点对应的时间、位置，外部输入一个时间，根据时间就能返回节点所对应的差值，根据差值就能把一个个点连接起来。在这里，对于路径漫游，要有一个完整的控制节点，每个节点坐标不是固定的，需要有个可视的编辑界面，用Unity3D内置的小球工具，可视的编辑它，每一个小球就是一个控制节点，它只是一个辅助参考，最终它不被显示。项目完成的算法是利用一个名为“path”的交结点，在下面建立若干个小球对象，每个小球作为Hermite曲线的一个控制点。如图3所示

图3 建立控制点Fig.2 Establishmentof control point

通过小球代替控制节点，实现了一个动态显示，利用Update函数，通过插值坐标，可以在运行过程中保证相机沿着小球来运动。为了使小球能够真正的达到和曲线实时调整的目的，用了画线的算法，理论的线是完全封闭连续的，由无数个点组成，而实际中都是由离散的点组成的，这是计算机本身的特点。用分段的折线段的方法来画线，其中折线段的每个点就是固化的坐标，根据折线段的每个位置而去确定固化的个数，段数分的越少，折线段就越生硬，但相对浪费的资源越少，最后固化这些点，把每个折线段的点存起来。在折线段编辑过程中，通过折线段，连成一个近似的封闭的方法，这里的折线段的段数是可以动态调节的。实时的调整折线段的段数，就可以观察到它的平滑程度，这样实现了节点的控制个数以及算法的复杂程度，达到一个优化的解决方法。

为了控制曲线画线，需要控制一个点，取控制点小球的坐标，将坐标存在数组里。通过当前用到的4个控制点，利用GetHermiteAtTime函数将坐标交给参数方程，通过运算算出当前坐标，根据坐标最终画出具体的线。那么当调节小球的时候，节点都随着变化，这样达到了直观形象的观察路径的方法。为了方便用户能看到行走的路径，利用OnDrawGizmos函数，调用Hermite曲线公式，在OnDrawGizmos函数中，每步通过时间做参数，找到当前的时间点，根据当前的时间点得到插值坐标，自动生成随着小球变化的蓝色路径，用户在编辑模式下就可看到曲线的变化。具体参数设置如图4所示。

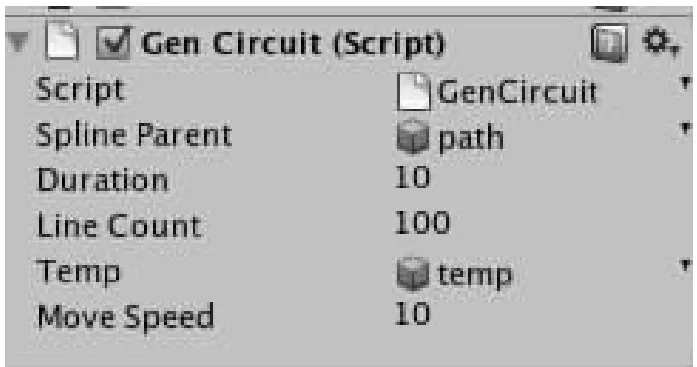
图4 算法参数设置Fig.4 Algorithm parameter settings

具体的参数说明如表1所示：

表1 算法中参数的功能说明Table1 Function description of parameters in the algorithm

用户可以在设置模式下根据要求增加和减少小球即控制点的数量，来控制曲线的光滑程度。通过Line Cout段数决定了曲线的弯折程度，段数越多，运行起来相对会比较慢，曲线会比较平滑，反之，段数越少，生成的曲线会比较生硬，最终根据需求生成用户满意的曲线。图5中A、B分别为Line Cout段数为10与100的对比效果。

图5 Line Cout段数对比图Fig.5 Number comparison chart

2.2 Animaiton编辑器与交互实现曲线的对比优势

在Unity3D环境中，系统提供的Animation编辑器可以实现固定漫游路径。就是将对象在相应时间、相应位置进行关键帧的设置。但是在编辑状态下，对象的每个关键帧位置并没有相应的参考标识，只能依靠估量的方法进行位置的设置，而且在漫游过程中，对象的朝向始终朝着一个方向，不能多视角的进行游览。如图6所示。

图6 关键帧设置Fig.6 Key Frames Settings

利用交互实现曲线的方法可以在编辑状态下看到生成的蓝色漫游路径，路径生成后可以随时调整控制小球的数量和位置来改变生成的漫游路径，具有实时化、可视化的特点。在漫游的过程中，摄像机的朝向可以随着鼠标方向的变化而变化，根据用户的意愿调整视角，使漫游方式更加人性化。相比较Animation编辑器生成漫游路径的方法，此方法步骤简便，生成的漫游路径十分平滑并且漫游方式更加符合用户的操作习惯。生成效果如图7所示。

图7 交互实现曲线Fig.7 Interactive curve

3 路径优化算法

生成路径时，如果在每次运行时在每一帧都重新进行矩阵运算来确定相机的位置，将大量占用计算机的系统资源，为了使程序运行更快，运行一次后，本项目将这一路径曲线进行插值离散化，将生成的曲线坐标保存到数组中，相机在漫游时完全脱离原始的控制点及矩阵运算，直接取数组中的坐标即可，这种将路径“固化”的方法能够大量节约虚拟漫游的系统资源。

用少量的球实现平滑的曲线，平滑的曲线由多条折线段构成，根据微积分的原理，折线段越多，曲线就越平滑，曲线的具体段数可由开发者根据场景大小自行设置。为了保证摄像机平滑运行，在每一帧调用Update函数，在函数中连接每一段折线段，将每段折线段生成的插值坐标赋值给摄像机，这样摄像机的运动时间与每一帧的时间细化同步，达到了平滑运动的目的。如此，摄像机的运动完全脱离Hermite曲线，这样就达到了优化算法的目的。如果开发者想改变控制小球的位置和数量生成新的Hermite曲线，要使改变生效，需要执行Savecode函数，Savecode函数的运行效果是把存有原有坐标的文本文件删除，生成存有新的Hermite曲线坐标的文件，程序再次运行时会调用新的坐标，从而使摄像机按照新的路径漫游。具体实现流程如图8所示。

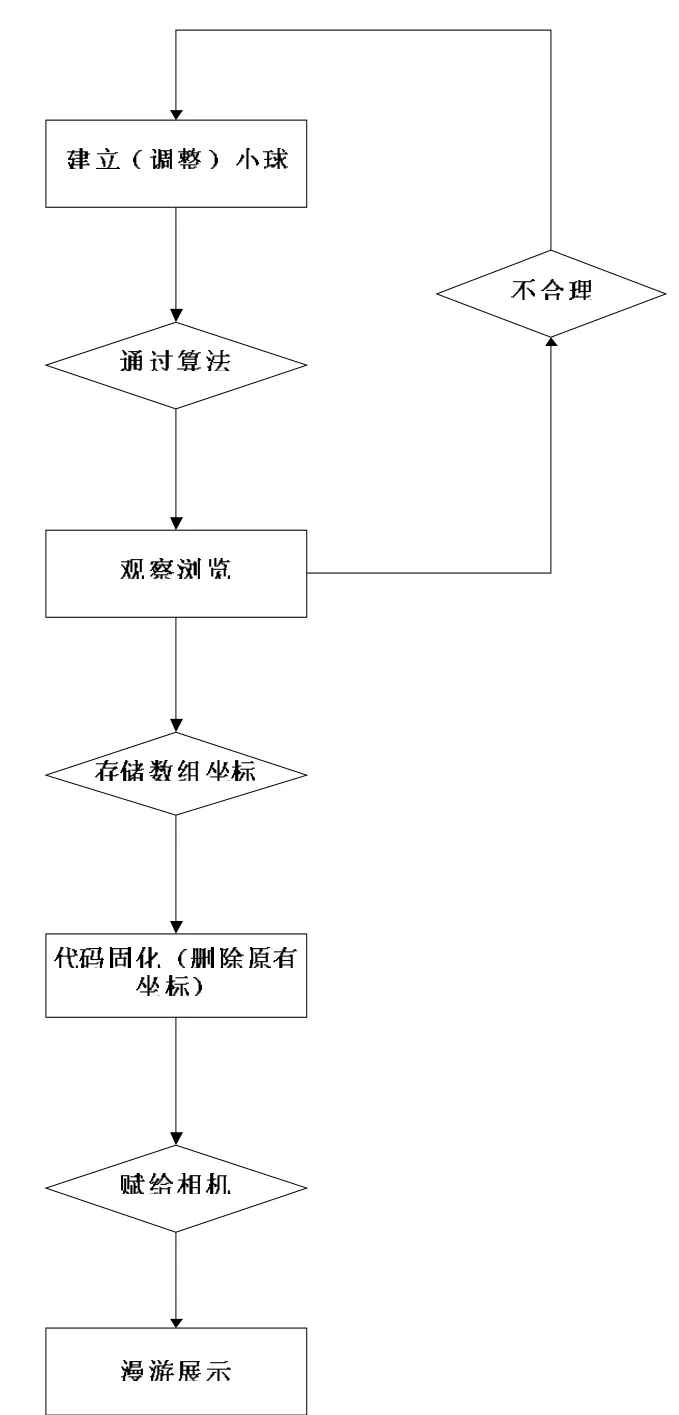
图8 流程图Fig.8 Flow diagram

4 结论

通过实验算法，利用路径的生成以及固化技术，实现了固定漫游路径。在虚拟景区展示中，用户根据图片导航[7]提示信息进入漫游界面，按照指定的路线，对重要景点进行游览，不仅方便于用户操作，而且不会遗漏欣赏到任何一个景点。这种算法也可以应用到游戏、旅游、教育、建筑等行业的虚拟场景中，如怪兽的自动行走，鸟的飞翔，车辆的自动行走，宇宙星体的运动等，对于今后虚拟行业的发展，具有良好的应用价值。

[1]徐诚.虚拟校园漫游系统的研究[D].武汉：华中师范大学，2006.

[2]李龙，向明尚，刘贤梅.虚拟校园环境的构造和漫游引擎的实现[J].大庆石油学院学报，2003，27（2）：56-58.

[3]陈勇，马纯永，陈戈．基于VC／OpenGL的虚拟海大校园导航系统[J].计算机辅助设计与图形学学报，2007，19（2）：263-266.

[4]孙英慧，孙英娟，杨柳.基于Hermite算法的曲线拟合[J].长春师范学院学报：自然科学版，2009，4（2）：8-12.

[5]Tomas A M，Eric H.实时计算机图形学[M].普建涛，译.2版.北京：北京大学出版社，2004.

[6]冯洪奎，鲍劲松，金烨，等.在视景仿真中用Hermite曲线控制物体运动[J].系统仿真学报，2008，5（4）：1224-1228.

[7]刘桂阳.大豆精准生产网络信息系统平台设计[J].黑龙江八一农垦大学学报，2008，20（5）：82-86.